鐵磁元件鐵心損耗的低頻測量方法

劉 鑫 姚陳果 梁仕斌 王俊凱 劉 濤

(1. 輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學) 重慶 400044 2. 云南電力試驗研究院(集團)有限公司 昆明 650051 3. 云南電力技術有限責任公司 昆明 650051)

?

鐵磁元件鐵心損耗的低頻測量方法

劉 鑫1姚陳果1梁仕斌2王俊凱1劉 濤3

(1. 輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學) 重慶 400044 2. 云南電力試驗研究院(集團)有限公司 昆明 650051 3. 云南電力技術有限責任公司 昆明 650051)

變壓器出廠實驗需要測量其空載勵磁特性、空載損耗和負載損耗。空載損耗主要是鐵損耗，測量空載損耗時往往要施加一個容量較大的工頻電源。為了減小實驗電源容量，使測量設備便攜化，提出一種采用低頻電源代替工頻電源測量鐵磁元件鐵心損耗的低頻測量法。該方法通過施加幾個頻率的低頻電壓，測量低頻下的鐵損耗PFe，得到不同頻率的E/f(電動勢/頻率)-PFe曲線，再通過樣條插值法計算頻率不同、E/f相等時的鐵損耗，根據最小二乘原理計算折算至工頻下的鐵損耗。并在單相變壓器和電流互感器中開展實驗，采用15,20,25Hz的折算結果與工頻50Hz實測結果的相對誤差ε<5%，相對誤差標準差σε<0.9。結果表明，該方法折算準確度高、穩定性好，并減小了實驗電源容量。

鐵磁元件 鐵心損耗 低頻法 最小二乘法 渦流損耗

0 引言

變壓器作為電力系統中最重要的輸變電設備，其性能好壞直接影響電力系統的安全、經濟運行。變壓器空載損耗和短路損耗是反映變壓器性能的重要參數，不僅反映變壓器的運行效率，也反映變壓器磁路的局部缺陷和使用壽命。《GB1094.1—2013 電力變壓器 第一部分：總則》要求空載損耗和短路損耗測量為例行實驗[1]；《JB/T 501—2006電力變壓器實驗導則》規定，進行空載實驗時，應從試品各繞組中的一側繞組(一般為低壓繞組)供給額定頻率的額定電壓，其余繞組開路[2]。但隨著電網電壓等級的提高，變壓器電壓等級和容量也逐漸增大，進行空載實驗時所需要的實驗設備容量、體積和重量往往很大，導致空載實驗程序復雜、操作人員人身安全得不到保障。

鐵心損耗的測量、計算在國內外已有較多研究。文獻[3]采用低頻電源測量鐵磁元件伏安特性的補償算法中考慮了鐵心損耗，補償算法的關鍵在于對鐵心損耗的補償。文獻[4]將鐵心損耗分為交變損耗和旋轉損耗，有限元仿真計算鐵心損耗并與實測值進行了對比。文獻[5-8]分析了直流偏磁對變壓器鐵心損耗的影響，直流偏磁下的鐵心損耗大于無偏磁下的鐵心損耗。文獻[9]分析了高頻變壓器的鐵損耗精確測量方法。文獻[10]仿真分析了磁通分布和鐵損耗的關系，可指導變壓器鐵心的設計。文獻[11,12]分別分析了鐵心損耗在不同頻率激勵下的鐵損耗變化規律。文獻[13-15]分析得出了變壓器鐵心飽和是勵磁涌流產生的主要原因。采用低頻法測量電力系統中鐵磁元件的鐵心損耗，能大大減小實驗電源容量，降低實驗成本，因此具有較大的工程實用價值。

本文采用低頻電源進行鐵磁元件空載實驗。測量低頻下的鐵心損耗，再根據相關算法折算至工頻實驗條件下，達到采用低頻實驗代替工頻實驗的目的。由于鐵磁元件鐵心飽和時的電壓基本與電源頻率呈正比，在低頻電源的激勵下，能夠成倍降低電源電壓，而電流基本相等，從而減小實驗電源的容量。

1 基本原理

本文采用幾個低頻率的正弦波電源來測量電力系統中鐵磁元件低頻下的渦流損耗和磁滯損耗，并根據相應折算算法得到折算至工頻實驗下的鐵心損耗。

1.1 鐵磁元件等效電路

鐵磁元件一側開路的等效電路如圖1所示。圖1中，Rdc為繞組上的直流電阻，Lσ為該側繞組漏感，Re為渦流損耗等效電阻，帶磁滯回環的非線性電感Lm為勵磁電感[16]，Lm中包含磁滯損耗Ph，iex(t)為勵磁電流，im(t)為流過Lm的磁化電流，ie(t)為渦流損耗等效電流，e(t)為感應電動勢，u(t)為施加在繞組上的勵磁電壓。

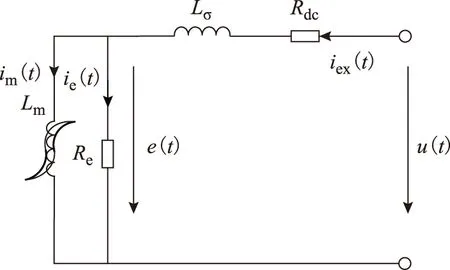
圖1 鐵磁元件等效電路Fig.1 Equivalent circuit of ferromagnetic components

由式(1)、式(2)[17]可知，當飽和程度(磁通Φ)相同時，磁化電流Im不變，而感應電動勢有效值E與頻率呈正比，空載時的漏感和直阻上的壓降很小，勵磁電壓U幾乎與電動勢E相等，因此勵磁電壓U幾乎與頻率呈正比。渦流電流Ie隨頻率減小，但Ie通常比Im小很多，從式(3)可得，勵磁電流Iex稍減小。由式(4)可知，實驗電源容量Spower基本與頻率f呈正比。因此隨著頻率降低，實驗電源容量大大減小。

E=4.44fNΦ

(1)

(2)

Iex=Ie+Im

(3)

Spower=UIex≈4.44fNΦIex

(4)

式中，S為鐵心橫截面積；H為磁場強度；l為磁路長度；N為鐵心匝數；μ為鐵心材料的磁導率。

1.2 鐵心損耗的組成

變壓器損耗是指在額定電壓下空載運行時變壓器鐵心所消耗的能量，其包括鐵心損耗PFe和空載電流在繞組中產生的銅耗PCu。而鐵心損耗又可分為磁滯損耗Ph、渦流損耗Pe和附加損耗。通常繞組銅耗和附件損耗都只占變壓器損耗的很小一部分，可忽略。因此本文主要分析磁滯損耗和渦流損耗。

大量實驗分析表明，磁滯損耗Ph的計算式為[17]

(5)

式中，Ch為磁滯損耗系數，其大小決定于材料的性質，與頻率無關；對一般硅鋼片，可取指數n=1.6～2.3；Bm為鐵心磁感應強度最大值；V為鐵心體積。

渦流損耗的計算式為[17]

(6)

式中，f為頻率；Ce為渦流損耗系數，其大小取決于材料的電阻率，與頻率無關；Δ為硅鋼片厚度[13]。

鐵心中磁滯損耗和渦流損耗之和為鐵心損耗，通常可用Steinmetz公式即式(3)進行計算。對于同一個鐵磁元件，其鐵心體積V、硅鋼片厚度Δ、磁滯損耗系數Ch、磁滯損耗系數Ce都是定值。因此如果保證不同頻率下的Bm一致，則可以認為We、Wh為常數。

=Whf+Wef2

(7)

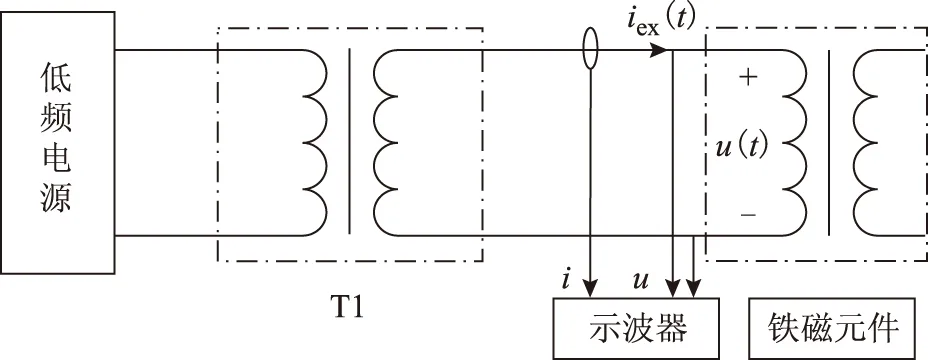
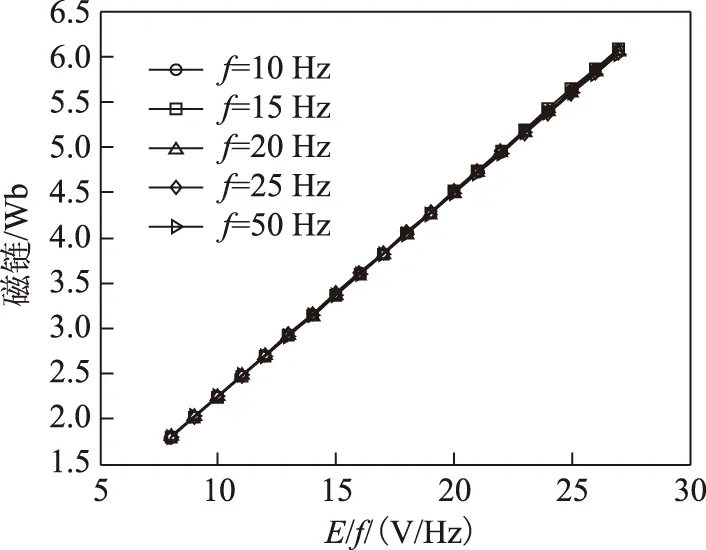
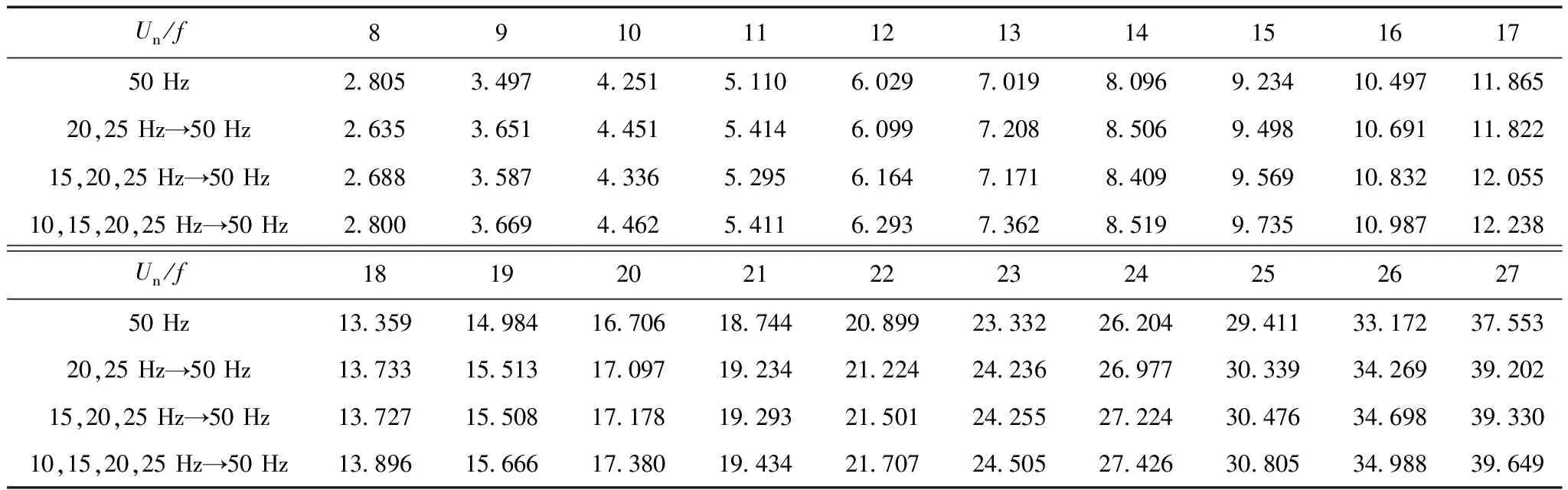
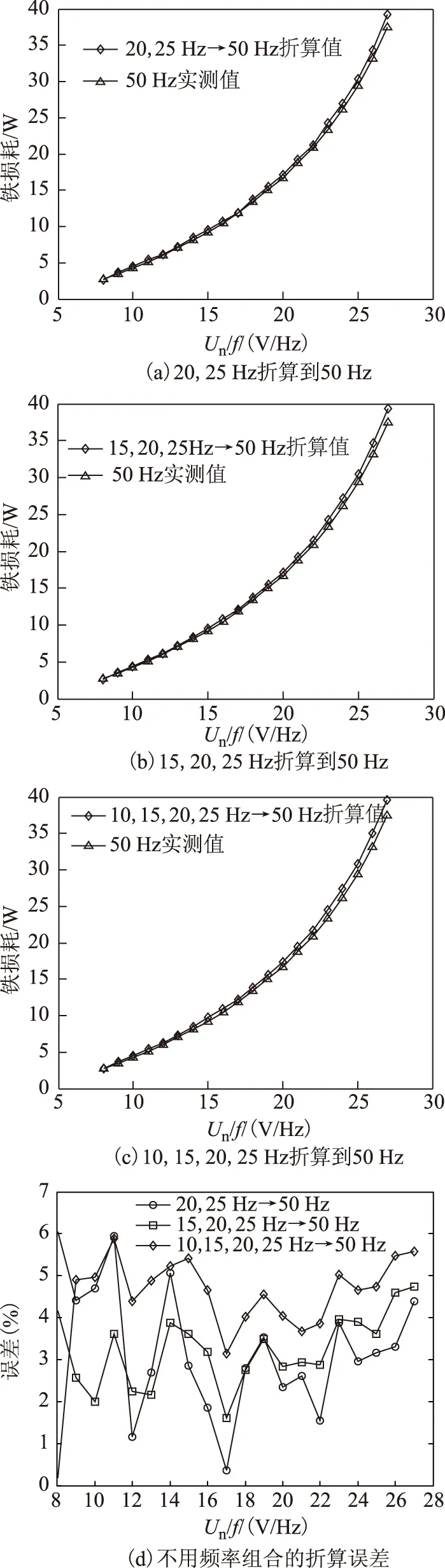
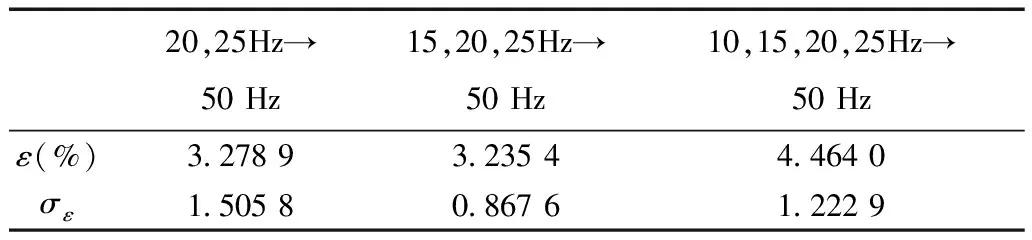
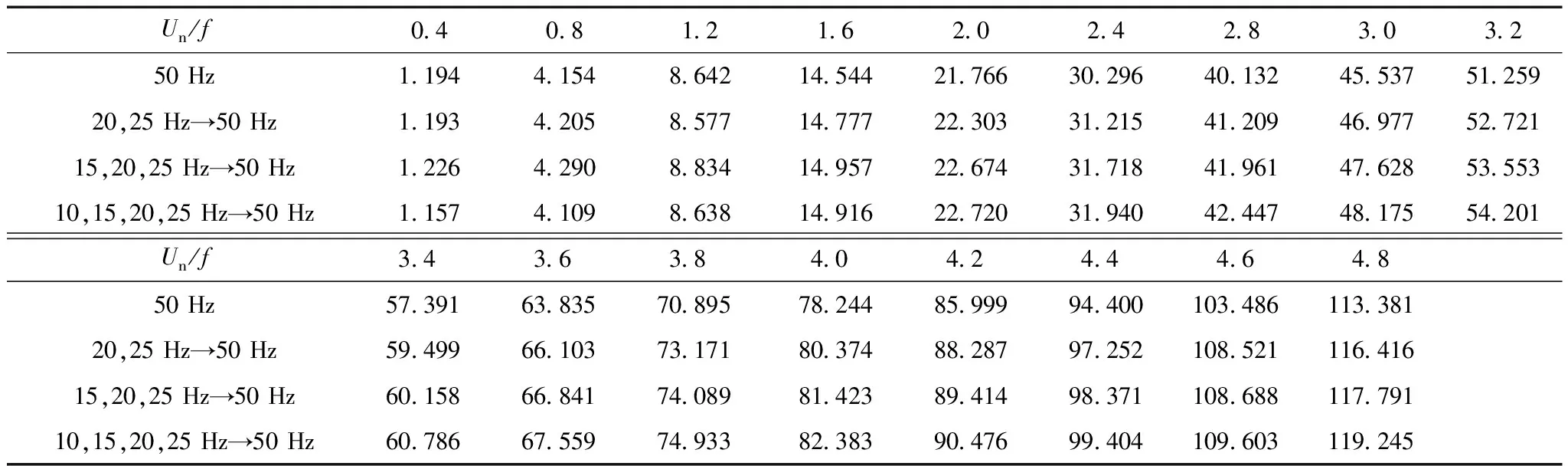
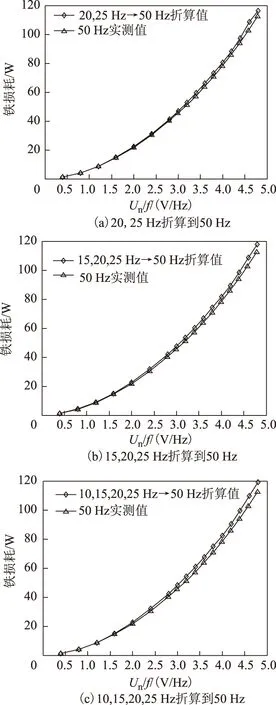
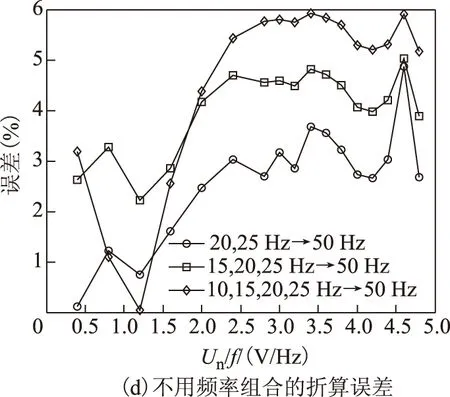
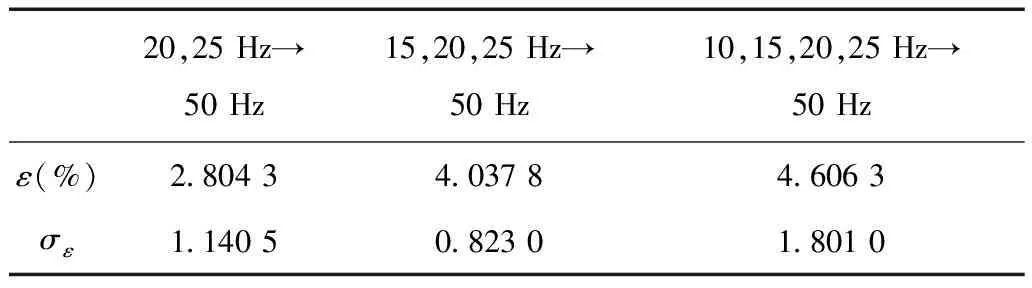
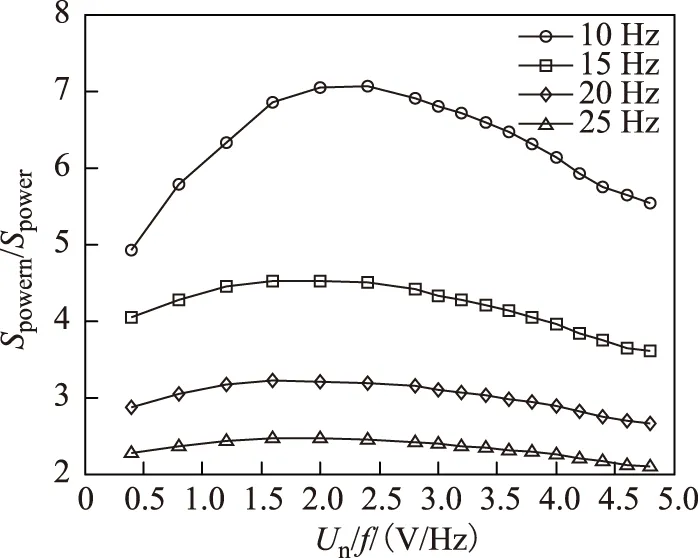
式中，Wh、We分別為每個磁化周期產生的單位磁滯損耗(W/Hz)和渦流損耗(W/Hz2)； 1 Hz

保持不同頻率下的磁通幅值相等，可通過兩個不同頻率下的鐵心損耗求出Wh和We，再代入工頻fn=50 Hz即可求得工頻下的鐵心損耗。由E=KvfNBmS(正弦波時Kv=4.44)[20]、Ψ=NBmS知，可通過計算鐵心磁鏈Ψ是否相等來判斷磁感應強度是否相等。

感應電動勢計算式為

(8)

磁鏈計算式為

(9)

式中,T為感應電動勢周期。

1.2 低頻法鐵心損耗的計算

考慮到采用兩個頻率計算的We和Wh可能具有一定的偶然性，為了使計算結果更加精確，本文采用多組頻率下的實驗數據來計算We和Wh。繞組一側開路，一側施加電壓，記錄電壓、電流數據。

鐵損耗的計算式為

(10)

計算各個頻率下對應的鐵損耗，PFem為第m個頻率下的鐵損耗，得到

(11)

將式(7)寫成矩陣形式為

FX=P

(12)

其中

式中，F為頻率矩陣；X為被求參數We、Wh組成的矩陣；P為鐵損耗矩陣。對于式(7)，采用最小二乘法可求得We和Wh。

X=(FTF)-1FTP

(13)

因此，折算到工頻下的鐵損耗為

(14)

式中，fn為額定頻率，一般為50Hz或60Hz。

鐵損耗電流可分為磁滯損耗電流與渦流損耗電流，即

(15)

式中，IFe、Ih、Ie分別為鐵損耗、磁帶損耗、渦流損耗對應電流的有效值。

由E=KvfNBmS可知，E與頻率f呈正比，因此渦流損耗電流ie與頻率呈正比，磁滯損耗電流ih與頻率無關。而不同頻率下Bm相等，所以im相等，折算到工頻下的勵磁電流為

(16)

折算到工頻下的勵磁電壓為

(17)

這樣便可得到折算到工頻的勵磁電壓Un與工頻損耗PFen的對應關系。值得提出的是本文方法的頻率適用范圍為1～60Hz。

2 實驗裝置及方法

2.1 實驗裝置

實驗裝置示意圖如圖2所示。其中，低頻電源采用PCR2000LE，用來產生頻率可變(0.1～999.9Hz)的正弦波；變壓器T1起升降壓的作用(電壓比可調，額定最高輸出電壓3.5kV)，同時還可以起到隔離直流的作用，消除直流偏磁的影響；示波器(力科HDO8000)記錄繞組兩端電壓、電流數據(電壓探頭：HVD3106，電流探頭：CP030A)；試品為變壓器、互感器等鐵磁元件。

圖2 實驗裝置示意圖Fig.2 Testing apparatus diagran

2.2 實驗方法與過程

為了驗證本文低頻折算法的準確性，選取型號為LMZ-3電流互感器和一臺配網動態模擬實驗室的單相變壓器為實驗對象。互感器參數：電流比為1 000A/1A，額定電壓為3kV，直流電阻Rdc1=4.902Ω(直阻儀測得)；變壓器參數：電壓比為380V/220V，額定容量為16.7kV·A，空載電流<1.5%，空載損耗<1.2%，阻抗電壓14%。低壓側直流電阻Rdc2=0.018 07Ω(直阻儀測得)，根據名牌參數和直阻計算得到低壓側漏感Lσ=6.432×10-4H。

按照圖2所示接線，變壓器從低壓側加壓，高壓側繞組開路;互感器從二次側加壓，一次側開路。分別施加四個頻率(10Hz、15Hz、20Hz、25Hz)的正弦波進行鐵磁元件空載實驗。由于實驗過程中E無法實時測量，因此實驗時保證不同頻率下U/f相同，記錄電壓、電流數據，再根據式(8)、式(10)計算得到不同頻率下的E/f-PFe曲線，采用三次樣條插值計算不同頻率、相同E/f下的鐵心損耗，最后根據式(10)～式(17)折算至工頻50Hz下鐵損耗PFen和勵磁電壓Un。分析采用低頻折算法的計算結果和50Hz實測結果的誤差。

3 實驗結果與分析

3.1 互感器實驗結果

設置示波器采樣點數為50 000，采集測試過程中的電壓、電流數據，采用Matlab對實驗數據進行分析。互感器(CurrentTransformer,CT)的漏感Lσ很小，計算時可忽略。

為了分析不同頻率下的Bm是否相等，按照式(8)、式(9)計算不同頻率下E/f相同時的磁鏈，結果如圖3所示。可看出當E/f相等時，磁鏈基本相等。

互感器在頻率不同、E/f值相同時的鐵心損耗如圖4所示，可看出頻率減小1/2，損耗約減小到1/3。

圖3 互感器頻率不同、E/f相等時的磁鏈Fig.3 The flux linkage of CT at different frequency under constant value of E/f

圖4 互感器頻率不同、E/f相等時的鐵心損耗Fig.4 Core loss of CT at different frequency and constant value of E/f

圖4 互感器頻率不同、E/f相等時的鐵心損耗Fig.4 Core loss of CT at different frequency and constant value of E/f

由于數據量較多，受篇幅限制，本文中沒有給出不同頻率下、不同電壓下鐵心損耗的實驗數據。

采用三次樣條插值法分別計算互感器在不同頻率、相同E/f下的鐵心損耗，并采用式(10)～式(17)計算推算至工頻50Hz下的損耗，得到Un/f-PFe曲線。比較Un/f相同時的折算值和工頻50Hz實測損耗，分析其測量誤差。表1為互感器不同頻率組合的折算結果與50Hz實測鐵心損耗的實驗數據對比。

表1 互感器低頻法和工頻法的鐵心損耗實驗數據對比

圖5為互感器在不同頻率組合的折算值與工頻50 Hz 實測結果的比較。可看出采用本文所述的低頻折算法折算值與工頻實測值有很好的吻合度。

圖5 互感器不同頻率組合的折算值與50 Hz實測值對比Fig.5 Comparison of test results at 50 Hz and conversion results of current transformer at different frequency combination

從圖5d可看出，幾種頻率組合下采用15,20,25 Hz 折算到50 Hz的折算相對誤差最小，每個點的相對誤差ε均不超過5%。幾種折算方法的折算相對誤差與誤差標準差σε見表2，由此可見采用三個頻率(15,20,25 Hz)折算到50 Hz的折算相對誤差平均值和標準差都更小，因此折算效果最好。

表2 互感器不同頻率組合折算誤差

3.2 變壓器實驗結果

互感器的漏感很小，基本可忽略，簡化了圖1中的等效電路。但是對于電壓等級高、容量大的變壓器而言，漏感相對較大，在電流較大時，漏感上的壓降不能忽略，因此采用式(8)計算變壓器的感應電動勢時，需要考慮變壓器漏感的壓降。認為漏感為空心電感，不產生有功損耗，且與頻率無關，因此式(10)對于變壓器同樣適用。本文在變壓器上展開實驗，分析該方法的折算效果。

變壓器在不同頻率、相同E/f值下的鐵心損耗如圖6所示，50 Hz下電壓最高加到約1.1Un(240 V)，變壓器出廠實驗值一般為1.1Un[2]。

圖6 變壓器頻率不同、E/f相等時的鐵心損耗Fig.6 Core loss of transformer at different frequency and constant value of E/f

同理，采用三次樣條插值法分別計算變壓器在不頻率、相同E/f時的鐵心損耗，計算推算至工頻50Hz下的損耗，得到Un/f-PFe曲線。比較Un/f相同時折算值和工頻50 Hz實測損耗，分析其測量誤差。

表3為變壓器不同頻率組合的折算結果與50 Hz鐵心損耗的實驗數據。圖7為變壓器不同頻率組合的折算值與工頻50 Hz實測結果的比較。從圖7可看出，變壓器采用本文算法與工頻實測值仍有很好的吻合度，驗證了本文方法的正確性。從圖7d可看出，幾種頻率組合下采用20,25 Hz和15,20,25 Hz折算到50 Hz 時，每個點的折算相對誤差ε仍均不超過5%。幾種折算方法的折算相對誤差與相對誤差標準差σε見表4，雖然采用20,25 Hz的相對誤差平均值較小，但是其標準差比采用15,20,25 Hz大，穩定性比采用三個頻率組合時差。

表3 變壓器低頻法和工頻法的鐵心損耗對比

圖7 變壓器不同頻率組合的折算結果與50 Hz實測值對比Fig.7 Coparison of test results at 50 Hz and conversion results of transformer at different frequency combination

20，25Hz→50Hz15，20，25Hz→50Hz10，15，20，25Hz→50Hzε(%)2 80434 03784 6063σε1 14050 82301 8010

圖8為變壓器采用不同頻率所需的實驗電源容量和工頻實驗所需的實驗電源容量的比較，縱坐標為工頻實驗電源容量Spowern與低頻電源容量Spower的比值。可以看出所需實驗電源容量的大小與頻率基本呈正比，曲線出現峰值的原因可能是低頻下的勵磁電流變化較快，使低頻下的實驗電源容量變化較快，而且頻率越低，Spowern/Spower變化越明顯，因此10 Hz時峰值現象最明顯。

圖8 不同頻率下的實驗電源容量Fig.8 The capacity of power supply under different frequency

4 結論

通過采用幾個頻率的低頻正弦波對鐵磁元件進行空載實驗，計算低頻下的鐵損耗，采用三次樣條插值計算不同頻率下E/f相等時的鐵損耗，采用本文提出的基于最小二乘原理的折算算法推算工頻50 Hz下的鐵損耗，并與工頻實測鐵損耗進行比較，可得到以下結論：

1)本文分別采用兩個頻率、三個頻率和四個頻率折算，綜合互感器和變壓器實驗結果，采用三個頻率折算的相對誤差和相對誤差標準差較小，穩定性較好，實際工程應用中建議采用三個頻率折算。

2)采用低頻法測量鐵磁元件鐵心損耗，可大大減小實驗電源容量。所需的實驗電源容量基本與頻率呈正比，缺點是要多次測量，但是如果后期能研制出自動化測量、分析設備，可極大地減少實驗成本和時間。

3)本文采用15,20,25 Hz三個頻率下的損耗計算工頻下的損耗與工頻實測損耗的相對誤差ε<5%，折算相對誤差標準差σε<0.9，具有較好的折算效果，后期可以考慮添加修正系數的方法修正不同頻率下的折算誤差，使測量精度更高。

[1] GB1094.1—2013,電力變壓器 第一部分: 總則[S].2013.

[2] JB/T 501—2006,電力變壓器試驗驗導則[S]. 2006.

[3] 梁仕斌, 文華, 趙涓, 等. 低頻變頻電源測量鐵磁元件伏安特性的一種補償計算方法[J]. 中國電機工程學報, 2010, 30(3): 125-129. Liang Shibin, Wen Hua, Zhao Juan, et al. A compensation calculation method for measuring ferromagnetic component volt-ampere characteristic using low frequency and frequency conversion power[J]. Proceedings of the CSEE, 2010, 30(3): 125-129.

[4] 張艷麗, 劉洋, 謝德馨, 等. 一種考慮硅鋼片旋轉損耗的三相變壓器鐵心損耗簡化計算方法[J]. 中國電機工程學報, 2013, 33(18): 126-131. Zhang Yanli, Liu Yang, Xie Dexin, et al. A simplified calculation method of core losses considering rotating losses of electrical steel sheets in three-phase transformers[J].Proceedings of the CSEE, 2013, 33(18): 126-131.

[5] 張艷麗, 彭志華, 謝德馨, 等. 直流偏磁下不同磁化曲線對變壓器鐵心損耗仿真的影響[J]. 電工技術學報, 2014, 29(5): 43-48. Zhang Yanli, Peng Zhihua, Xie Dexin, et al. Effect of different magnetization curves on simulation for transformer core loss under DC bias[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 43-48.

[6] 趙小軍, 崔燦, 李琳, 等. 基于定點諧波平衡法的鐵心磁滯與損耗特性分析[J]. 電工技術學報，2014, 24(5): 46-51. Zhao Xiaojun, Cui Can, Li Lin, et al. Analysis of the hysteresis and loss characteristic in the laminated core by fixed-point harmonic-balanced method[J].Transactions of China Electrotechnical Society, 2014, 24(9): 46-51.

[7] 趙小軍, 李琳, 程志光, 等. 定點諧波平衡有限元法與疊片鐵心直流偏磁磁化特性研究[J]. 中國電機工程學報, 2011, 31(9): 126-132. Zhao Xiaojun, Li Lin, Cheng Zhiguang, et al. Fixed point harmonic-balanced finite element method and DC-biasing magnetizing characteristic of laminated core[J]. Proceedings of the CSEE, 2011, 31(9): 126-132.

[8] 郭滿生, 梅桂華, 張喜樂, 等. 直流偏磁條件下單相三柱電力變壓器損耗計算[J]. 電工技術學報, 2010, 25(7): 67-71. Guo Mansheng, Mei Guihua, Zhang Xile, et al.Calculation of losses in single phase three limb transformer under DC-biasing[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 67-71.

[9] Mu Mingka, Li Qian, David J G, et al. New core loss measurement method for high-frequency magnetic materials[J].IEEE Transactions on Power Electronics , 2014, 29(8): 4374-4381.

[10]Tenyenhuis E G, Mechler G F, Girgis R S. Flux distribution and core loss calculation for single phase and five limb three phase transformer core designs[J]. IEEE Transactions on Power Delivery, 2000, 15(1): 204-209.

[11]Ibrahim M, Pillay P.Advanced testing and modeling of magnetic materials including a new method of core loss separation for electrical machines[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1507-1515.

[12]Hasan S, Taib S, Hardi S, et al. Core loss characteristics analysis of power transformer under different frequencies excitation[C]//7th International Power Engineering and Optimization Conference, Langkawi, 2013: 619-623.

[13]何小慶, 劉淑萍, 李攀宏, 等. 一種消除單相變壓器勵磁涌流的預充磁策略[J]. 電力系統保護與控制, 2014, 42(17): 120-124. He Xiaoqing, Liu Shuping, Li Panhong, et al. Eliminating the single-phase transformer inrush current based on pre-magnetizing[J]. Power System Protection and Control, 2014, 42(17): 120-124.

[14]傅偉, 趙莉華, 梁勇, 等. 多臺變壓器空載合閘勵磁涌流及其抑制方案的研究[J]. 電力系統保護與控制, 2015, 43(1): 28-33. Fu Wei, Zhao Lihua, Liang Yong, et al. Study on no-load closing inrush current of transformer group and suppression measures[J]. Power System Protection and Control, 2015, 43(1): 28-33.

[15]姚東曉, 鄧茂軍, 倪傳坤, 等. 變壓器多側勵磁涌流產生機理及對差動快速動作區影響研究[J]. 電力系統保護與控制, 2016, 44(5): 36-41. Yao Dongxiao, Deng Maojun, Ni Chuankun, et al. Transformer′s multi-side inrush current generation mechanism and its influence on the differential protection′s fast action zone[J]. Power System Protection and Control, 2016, 44(5): 36-41.

[16]León F D, Farazmand A, Jazebi S, et al. Elimination of residual flux in transformers by the application of an alternating polarity DC voltage source[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1727-1734.

[17]湯蘊璆.電機學[M]. 北京: 機械工業出版社, 2011.

[18]Steinmetz C P. On the law of hysteresis[J]. Proceedings of the IEEE, 1984, 72(2): 196-221.

[19]Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.

[20]朱春波, 徐德鴻, 張龍龍, 等. 應用于電力電子技術的變壓器和電感——理論、設計與應用[M]. 北京:機械工業出版社, 2014.

(編輯 張洪霞)

Core Loss Measurement of the Ferromagnetic Components Using Low-Frequency Method Frequency Power Supply

LiuXin1YaoChenguo1LiangShibin2WangJunkai1LiuTao3

(1.State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China 2.Yunnan Electric Power Test & Research Institute (Group) Co.Ltd Kunming 650051 China 3.Yunnan Electric Power Technology Company Kunming 650051 China)

Transformers will have measured no-load excitation characteristics, no-load loss and load loss for factory tests. Generally, a large capacity of industrial-frequency (IF) power supply is needed to measure the no-load loss which mainly consists of core loss. In order to reduce the capacity of testing power supply and make the test equipment portable, a low-frequency power supply rather than IF power supply which was used for core loss measurement of ferromagnetic components, was demonstrated in this paper. By applying several low frequencies voltages, the cure ofE/f-PFe(electromotive force/frequency-core loss) via calculating core loss under low-frequency can be first obtained. Core loss under low-frequency of different frequency at constant value ofE/fwere then calculated through spline interpolation method. Lastly, the converted core loss under IF was determined based on least square method. In addition, experiments were conducted on the current transformer (CT) and single phase power transformer, comparing conversion results which using 15,20,25 Hz with directly measured results under IF, the relative errorεis below 5% and standard deviation of relative errorσεis less than 0.9, respectively. These results show that this method possesses high conversion accuracy and stability and reduces the capacity of testing power supply obviously.

Ferromagnetic components, core loss, low-frequency method, least squares method, eddy loss

中國南方電網有限責任公司科技項目資助(K-YN2014-136)。

2016-04-06 改稿日期2016-05-28

TM416

劉 鑫 男，1992年生，碩士研究生，研究方向為互感器、變壓器等設備檢測方法。

E-mail：alxenderking@cqu.edu.cn(通信作者)

姚陳果 男，1975年生，教授，博士生導師，研究方向為變壓器在線監測技術和脈沖功率技術在生物醫學中的應用。

E-mail：yaochenguo@cqu.edu.cn