電工軟磁材料旋轉磁滯損耗測量及建模

張長庚 楊慶新,2 李永建

(1. 河北工業大學電磁場與電氣可靠性省部共建重點實驗室 天津 300130 2.天津工業大學電工電能新技術天津市重點實驗室 天津 300387)

?

電工軟磁材料旋轉磁滯損耗測量及建模

張長庚1楊慶新1,2李永建1

(1. 河北工業大學電磁場與電氣可靠性省部共建重點實驗室 天津 300130 2.天津工業大學電工電能新技術天津市重點實驗室 天津 300387)

電力變壓器和電機中存在旋轉鐵心損耗是其損耗預測不準的主要原因之一。針對該問題，提出電工軟磁材料旋轉磁滯損耗測量及建模方法。首先，矢量磁滯損耗分解為切向損耗和法向損耗兩部分，分別根據圓形旋轉損耗和交變損耗建模。其次，對軟磁復合材料和無取向電工鋼片進行模型參數辨識，并比較兩種材料的損耗特性和模型參數。最后，利用三維磁特性測量裝置進行多種勵磁模式下的損耗測量，并對比實驗結果與模型預測值。結果表明，在旋轉復雜激勵下，所提出的模型比傳統的Steinmetz模型有更高的精度。

電機鐵耗 磁滯損耗 電磁場數值模擬 旋轉損耗

0 引言

高效率的電機和電力變壓器的使用能夠節約社會總能源消耗，是響應國家節能減排發展戰略的有效措施。設計高效率的電機和電力變壓器，一方面改進或提出新的結構、工藝和控制策略，例如三維磁通電機；另一方面減少磁性材料本身的鐵耗，例如采用新型非晶納米晶材料[1]。兩方面都依賴準確的鐵心材料的磁特性測量和建模。早在電機等電磁裝置用于工業生產之初，1892年S.Steinmetz提出了著名的磁滯損耗計算Steinmetz公式[2]。該公式適用于正弦穩態下的損耗預測，隨著HVDC和電力電子設備的廣泛應用，大量諧波引入電機和變壓器設備，為解決復雜磁通密度波形的激勵，提出了多種修正的Steinmetz公式。文獻[3] 引入等價頻率的概念，考慮非正弦磁通密度勵磁下的損耗改進Steinmetz公式。文獻[4]提出廣義的Steinmetz公式，進一步考慮小磁滯回環對損耗的貢獻。文獻[5]考慮頻率和磁通密度對Steinmetz公式系數的影響，通過擬合變系數的公式，提高損耗計算精度。文獻[6]考慮電力變壓器的雜散損耗和屏蔽鋼板的鐵耗。為了獲得更高精度磁滯損耗的估計，各種經典標量磁滯模型，如Preisach模型、Play模型和Jiles-Atherton(JA)模型等相繼被提出。

在電力變壓器和電機實際運行中發現旋轉磁場激勵下損耗大于單方向的交變損耗。對旋轉損耗的研究分為兩類：①基于Steinmetz公式方法和矢量磁滯模型方法，文獻[7]在頻域空間把二維空間磁通密度B軌跡分解為圓形旋轉磁通密度和交變磁通密度兩部分，根據交變損耗系數和旋轉損耗系數分別利用Steinmetz公式進行損耗估計；②建立矢量的磁滯模型，如新型混合矢量磁滯模型。文獻[8]利用Stoner-Wohlfarth模型求解磁滯算子矢量磁化強度方向，再利用Preisach模型矢量加和所有單個磁滯算子的磁化強度。因而，準確的磁滯模型和損耗模型有助于從鐵心磁化本質上理解變壓器的磁化和損耗特性，解決相應的工程問題如勵磁涌流問題[9,10]。基于磁滯模型的損耗計算方法，通過有限元方法耦合標量或矢量磁滯模型，解法器迭代次數多，算法復雜計算量大[11,12]；基于Steinmetz公式類交變損耗和旋轉損耗方法，計算過程簡單但精度較低[13]，廣泛用于電機本體設計和效率分析[14]。傳統Steinmetz公式是穩態計算方法，為了避免電磁有限元計算存儲每一步的計算結果，文獻[15] 提出瞬態的Steinmetz計算方法，有效減少了計算量。

無論是材料的精確磁滯模型還是Steinmetz公式的經驗模型，模型應用的前提是參數的辨識，首先獲得模型所需要的材料磁特性測量數據。可靠的材料模型數據獲得依賴準確的可重復的磁特性實驗測量。電工鋼片一維國家測量標準是愛潑斯坦方圈方法；國際上一些科研團隊研制了不同結構形式的二維單片磁特性測量系統，根據勵磁結構和磁化樣品的不同，可分為水平形式方形樣片旋轉測量儀[16]、水平圓形樣片旋轉測量儀[17]、垂直型旋轉測量儀等[18]。悉尼科技大學針對軟磁復合材料研發了首個三維軟磁材料磁特性測量儀[19]。國內沈陽工業大學對硅鋼片軟磁材料進行了二維磁特性測量[20]。河北工業大學研制了寬頻(20～1 000Hz)大功率軟磁材料的三維磁特性測量裝置[21]。

本文提出一種基于旋轉磁特性測量的瞬態矢量磁滯損耗模型。該模型統一描述了交變磁滯損耗和旋轉磁滯損耗，能夠預測對空間任意磁通密度軌跡的瞬時磁滯鐵耗。其基本原理是將空間磁通密度軌跡的運動分解為切向運動和法向運動，其中法向磁通密度軌跡運動采用交變損耗計算，切向磁通密度運動采用旋轉損耗計算方法。利用三維磁特性測量裝置對無取向硅鋼片進行交變損耗、旋轉損耗和變軸比的橢圓激勵的磁滯損耗測量。根據本文提出的矢量磁滯損耗模型，預測了變軸比的復合型橢圓激勵下的磁滯損耗，驗證了該模型的有效性。

1 旋轉損耗模型的定義

1.1 改進矢量磁滯模型的定義

本文基于傳統的矢量Play磁滯模型[12]提出考慮旋轉磁化的改進型矢量磁滯模型。傳統的矢量Play模型依賴于圓形磁滯算子Hk(H)的疊加運算，即

(1)

式中，B為磁通密度；H為磁場強度；n為磁滯算子的數量；fk為非線性的映射函數從磁場強度空間映射到磁通密度矢量空間；Hk(H)為圓形的Play磁滯算子。磁場強度超前的空間距離即為磁滯算子半徑。

圖1為軟磁材料橢圓磁化軌跡和改進磁滯模型，圖中橢圓表示磁滯算子，橢圓形磁滯算子的邊界到算子中心的空間距離表示磁場強度的空間超前矢量，磁滯算子隨磁化軌跡的運動而運動。磁滯算子橢圓長軸和短軸在不同空間位置的長度表征磁性材料磁特性，根據二維或三維矢量磁特性測量建模和辨識。橢圓圓心表示無磁滯磁場強度Hnon，橢圓形算子的長軸或短軸之一位于橢圓圓心與坐標原點的連接線上。算子的圓心位于磁化軌跡的圓弧上，表示無磁滯的磁場強度軌跡。磁場強度軌跡逆時針旋轉，相應磁通密度軌跡也逆時針旋轉，兩者關系由磁場飽和、磁場各向異性和磁滯等因素決定。dB/dt的射線代表磁通密度矢量的空間變化方向，一維dB/dt表示磁通密度的增加或減少，從而決定磁場強度超前于磁通密度的方向。

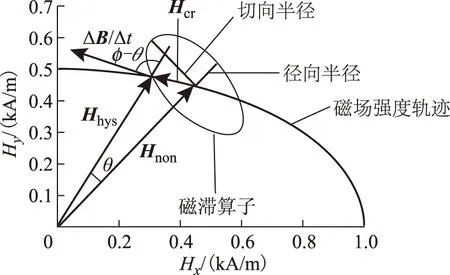
圖1 軟磁材料橢圓磁化軌跡和改進磁滯模型Fig.1 The elliptic magnetization locus of soft magnetic material and the improved hysteresis model

宏觀磁場強度Hhys分解為兩部分，即

Hhys=Hnon+Hcr

(2)

式中，Hcr為矯頑磁場強度；Hnon僅為磁通密度B的函數。Hcr是在橢圓中心點處作斜率為dB/dt的射線與磁滯算子的相交線段。當交變勵磁時，dB/dt的射線沿軌跡的軸線方向；當圓形勵磁時，射線沿圓形軌跡的切向方向；當橢圓形勵磁時，射線位于兩者之間。Hnon計算式為

Hnon=g(B)

(3)

對于各向同性材料，矢量Hnon方向與B方向相同，函數g的幅值可選為正切函數或Langevin函數；對于各向異性軟磁材料函數，g是空間二維矢量函數。綜上，矢量磁滯模型的計算流程如圖2所示。

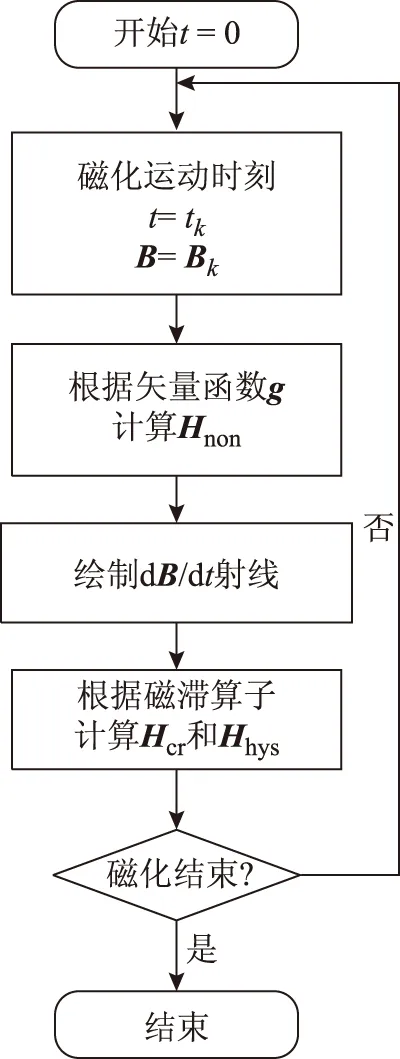
圖2 改進磁滯模型計算流程Fig.2 Control flow chart of improved hysteresis model

本文提出的改進矢量磁滯模型與傳統的矢量Play模型區別如下：

1)矢量Play模型以磁場強度H為變量，而改進模型以B為變量，因此后者也被稱為磁滯逆模型。當進行基于磁矢位A的有限元分析時，逆磁滯模型避免迭代運算，提高了計算效率。

2)傳統矢量Play模型磁滯算子為圓形，改進模型磁滯算子為橢圓形且考慮了旋轉磁化過程。

3)兩種模型中的非線性映射函數是一對互逆的函數。

1.2 矢量磁滯損耗分解

軟磁材料的比損耗，即單位時間內的磁場做功，計算式為

(4)

Hnon磁場分量瞬時吸收或釋放能量，但一個周期內做功的積分為零。磁通密度增加時儲存靜磁能，磁通密度減小時釋放靜磁能，本質上不消耗能量，從而使磁性器件外特性為感性。磁滯能量的耗散僅來自于矯頑磁場Hcr部分，如圖1所示，矯頑磁場部分依賴橢圓形磁滯算子進行插值計算，Hcr總是超前于無磁滯的磁場強度Hnon。商用軟件如Ansys-Maxwell中，矯頑磁場強度沿直角坐標系正交分解為兩部分，即

Hcr=Hxcrix+Hycriy

(5)

式中，Hxcr、Hycr分別是x、y方向的矯頑力。則總磁滯損耗相應分解為兩部分之和，即

(6)

直角坐標系下的正交分解不能有效表征旋轉磁滯損耗的物理過程。旋轉磁化的鐵磁學機理是磁疇壁的旋轉，而在低場強的交變磁化時本質是磁疇壁的移動。實驗發現接近飽和時的旋轉磁滯損耗接近于零，因此理論上矯頑磁場強度也應該為零。式(5)中，Hxcr、Hycr獨立采用交變矯頑力建模方法，故式(6)計算的兩個方向獨立的交變損耗之和大于旋轉磁化損耗，這與實驗結果不符。

為了解決該問題，本文將矯頑磁場強度分解為法向和切向兩部分。橢圓的兩個軸分別是切向軸和法向軸，法向軸與坐標原點和橢圓中心連線重合，切向軸與連線垂直。沿法向軸分解的磁損耗受交變磁化影響，沿切向軸分解的磁損耗受旋轉磁化影響，則

(7)

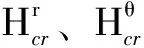
1.3 幅值交變磁滯損耗建模

幅值矯頑磁場強度的建模，根據等價的橢圓模型，假設勵磁波形是標準正弦，矯頑磁場強度符合余弦規律變化，則

(8)

式中，Bm為磁化歷史記錄的最大磁通密度；Hm為最大的矯頑力；ω為時變磁場的角頻率。聯立式(4)和式(8)，幅值交表磁滯損耗簡化為

(9)

式中，f為勵磁頻率。根據Berotti損耗分離定律交變磁滯損耗假設得

(10)

式中，kh為磁滯損耗系數。式(7)與式(6)聯立解得

(11)

故瞬時交變磁滯損耗計算式為

(12)

式中，Br為矢量B在橢圓軌跡法向方向的分量，當交變磁化時Br為矢量B的幅值。

1.4 旋轉磁滯損耗建模

圖3為軟磁材料圓形旋轉磁化過程磁場強度，磁通密度幅值Br不變，B滯后于H空間角度θ，且θ是圓形旋轉磁通密度幅值Br的函數。當磁性材料的磁化軌跡為圓形時，瞬時功率式(4)簡化為

(13)

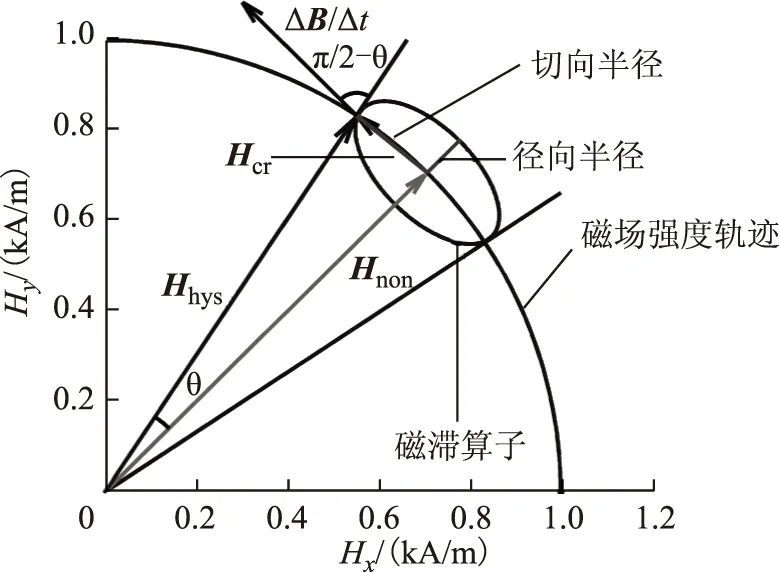
圖3 軟磁材料圓形旋轉磁化過程磁場強度Fig.3 Soft magnetic material magnetic field intensity of rotational magnetization process

(14)

在有限元計算中，Hnon可以通過磁通密度非線性關系直接計算，H通過磁滯模型計算，故切向計算式更實用。由于磁性材料SMC和無取向鋼片都存在一定的空間各向異性，當磁通密度軌跡運動時，空間角度差θ不恒定。為了進一步簡化損耗模型，取空間角度差的積分平均值作為損耗模型的特征參數，即

(15)

式中，α為磁通密度矢量的空間角度。

(16)

式中，B1為基波幅值。由于磁性材料的非線性，磁場強度H產生高次諧波的畸變為

(17)

式中，Hi為各奇次諧波幅值；θi為各次諧波相位。單位時間平均功率的積分表達式為

(18)

式中，θ1為Hx的基波分量與Bx基波的相位差。式(18) 說明對于圓形磁通密度的勵磁模型，旋轉損耗僅決定于基頻下的相角差θ1，Hx、Hy的高次諧波部分對磁滯損耗無貢獻。此時H1僅是H基波的幅值，故在式(12)增加修正系數，即

(19)

當樣品未達到飽和時，系數k≈1； 當樣品過飽和時，系數k略小于1。進一步給出損耗模型旋轉部分的計算式為

(20)

綜上，通過式(12)和式(20)分別計算幅值交變損耗和切向瞬時旋轉損耗。文獻[7]中旋轉損耗的分解算法是在頻域下，需要有限元后處理存儲每一時刻每一網格位置的磁場。本文提出的算法在時域進行磁通密度軌跡的分解，顯著節約內存，降低計算量。

2 損耗模型辨識方法

根據本文提出的旋轉損耗模型對軟磁復合材料SMC-Somaloy500和無取向硅鋼片35WW270進行模型參數的辨識和數值實現。

2.1 交變損耗模型參數辨識

無論采用哪種動態磁特性測量方法，在交變或旋轉激勵下，磁性材料測量總鐵耗不僅包含磁滯損耗Ph而且含有經典渦流損耗Pc和異常損耗Pe。隨著勵磁頻率的升高，渦流損耗和異常損耗在總損耗的占比增加起主導作用。僅在極低測量頻率(1Hz)時，可忽略剩余兩部分，認為測量損耗僅是磁滯損耗。常用的實驗損耗分離和處理方法是根據經典的Steinmetz公式理論，將磁性材料總損耗Pv進行理論分解，即

(21)

式中，kh、kc、ke分別為交變磁滯損耗系數、渦流損耗系數和異常損耗系數。

通過測量多個頻率的Bm-P損耗曲線，擬合模型損耗參數，求解最優化問題，即

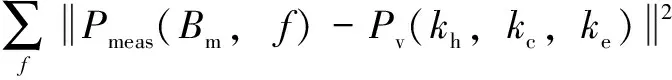
(22)

優化問題采用基因算法求解。對于無取向硅鋼片的優化擬合,采用20Hz、50Hz、100Hz和200Hz的損耗測量數據；對于SMC材料,采用20Hz、100Hz和200Hz的損耗測量數據進行辨識。

圖4是無取向鋼片和SMC兩種材料20～200Hz的Bm-P損耗曲線，通過Steinmetz公式得到的計算值的擬合結果和測量結果吻合較好。SMC鐵耗在低磁通密度時遠高于無取向鋼片，隨著頻率升高，鐵耗中渦流損耗占比不斷增大，兩者的總鐵耗差距縮小。當交變勵磁頻率為200Hz時，SMC鐵耗高于35WW270一倍。

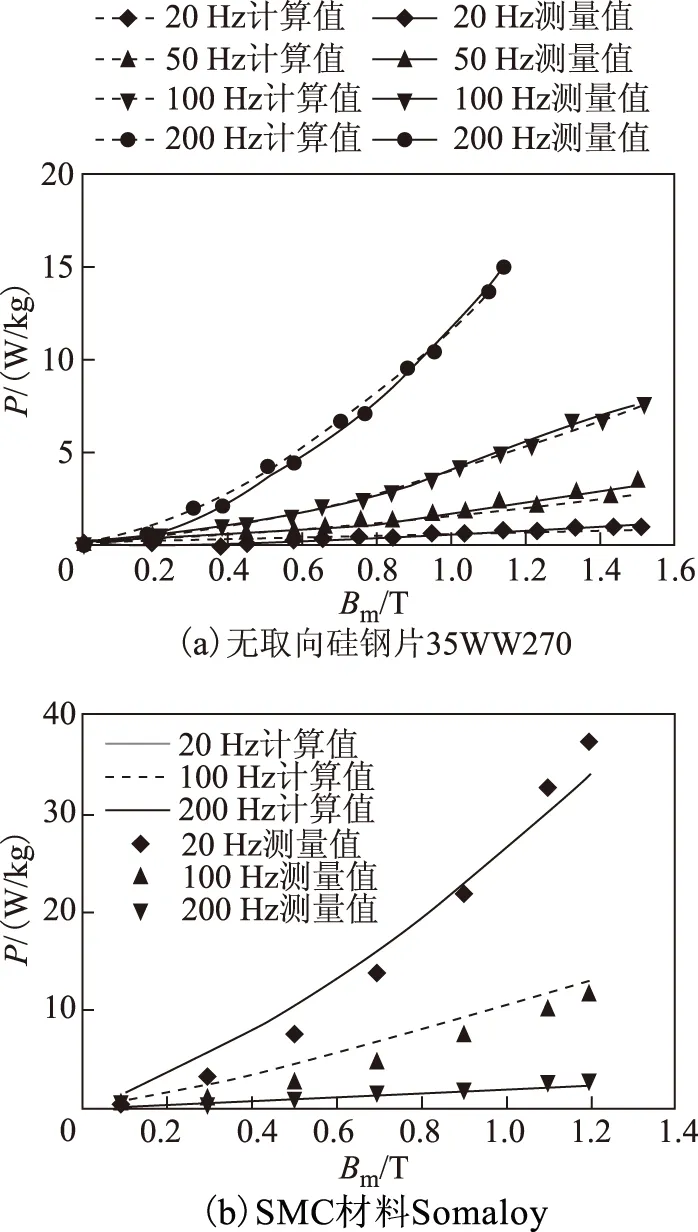
圖4 兩種材料的Bm-P曲線Fig.4 Bm-P curves of two materials

表1為無取向鋼片和SMC材料的Steinmetz損耗系數，是通過在寬頻(20～200Hz)下的交變損耗曲線擬合得到。該模型認為擬合的損耗系數不隨頻率的變化而變化，但是總損耗與頻率的關系是β倍頻、2倍頻和1.5倍頻三部分的組合關系。SMC材料的磁滯損耗系數遠大于無取向硅鋼片，SMC異常損耗系數小于無取向鋼片。根據實驗數據，兩者渦流損耗系數相差不大。SMC材料的渦流損耗機制復雜，不僅依賴于微小鐵基顆粒的尺寸而且依賴絕緣層的絕緣性能；既存在鐵基小顆粒內部的微觀渦流，也存在穿過絕緣層的宏觀渦流[22]。

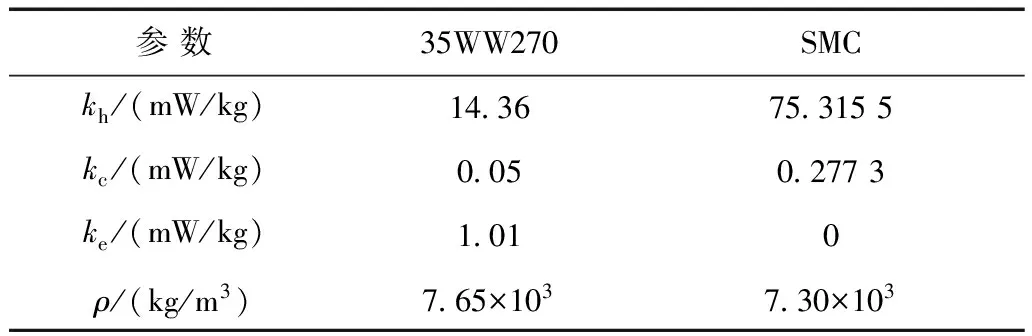
表1 兩種材料的損耗系數

對于硅鋼片材料,當交變勵磁或旋轉勵磁時，硅鋼片內部渦流Jx和Jy僅在沿疊片方向有顯著變化，在平行疊片的平面內變化不顯著。任意復雜勵磁下，硅鋼疊片的三維渦流場問題可分解為x、y方向的獨立交變磁化過程，分別用一維渦流方程描述[23]，因此渦流損耗也可相應地分解為x、y方向交變渦流損耗。類似地，假設異常損耗也可分解為x、y方向獨立的交變異常損耗，使用交變損耗辨識的kc、ke系數。故瞬時渦流損耗功率和異常損耗功率分別表示為

(23)

(24)

根據式(23)和式(24)，從測量的總鐵耗中去除渦流損耗和異常損耗部分，剩余部分即不隨頻率變化的磁滯損耗，采用本文算法進行模型驗證。

2.2 旋轉損耗模型參數辨識

軟磁材料的旋轉磁特性測量方法沒有統一的國際標準，國內外實驗室廣泛采用控制圓形或橢圓形B軌跡的勵磁模型為

(25)

式中，εy為橢圓軌跡軸比。標準的圓形磁軌跡(εy=1)不包含諧波，易于損耗建模和特征參數的提取，同時反映軟磁材料磁各向異性和旋轉磁損耗特性。當εy=0時，勵磁模型退化為單軸的交變勵磁，反映了軟磁材料的單軸交變損耗特性。在電力變壓器的T型接口處，磁通密度的軌跡接近菱形，可采用橢圓形磁通密度軌跡近似模擬。

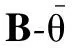
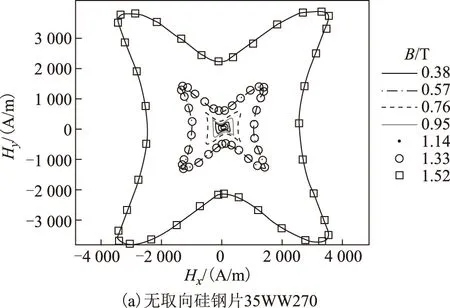
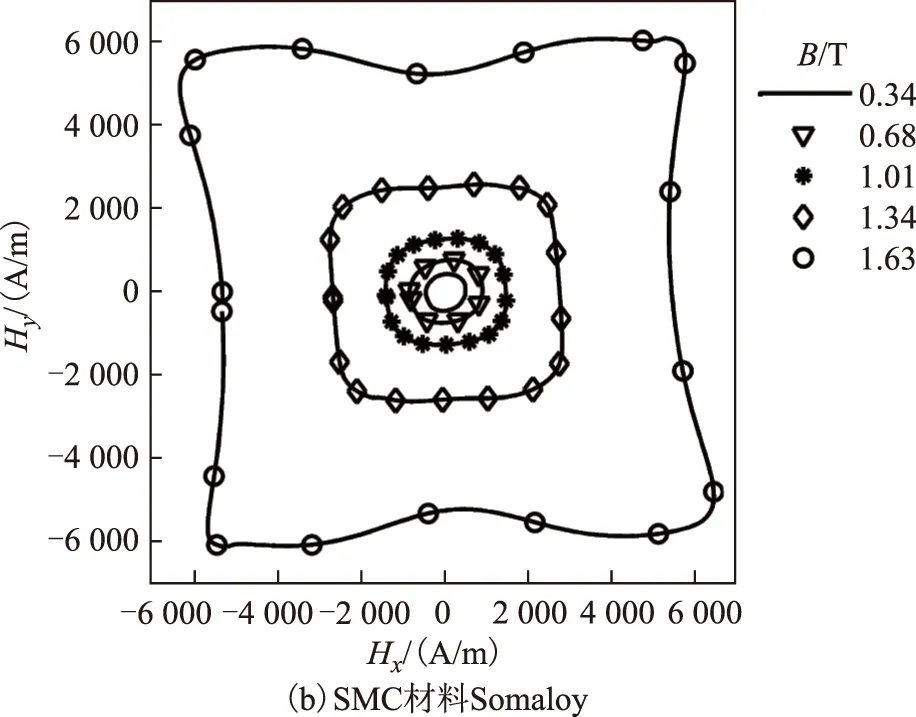
圖5 圓形激勵下50 Hz磁場強度軌跡Fig.5 Trajectory of 50 Hz magnetic field under circular excitation

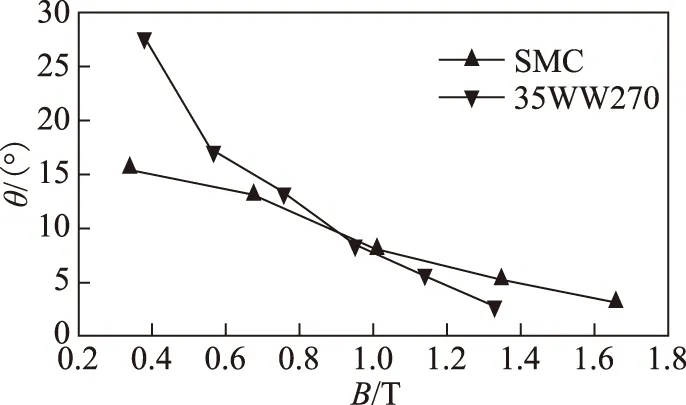
圖6 旋轉磁化磁通密度幅值與空間夾角關系Fig.6 Relationship between amplitude and space angle of the rotation magnetization

3 旋轉損耗模型實驗驗證

3.1 三維磁特性測量

三維磁測量裝置的主磁路由三對正交的C型鐵心和六個多層柔性勵磁線圈組成，如圖7所示[21]。勵磁裝置的測量樣品是SMC樣品或硅鋼疊片。樣品切割或疊置為邊長為22mm的立方體，放置于B-H復合立方體傳感箱內，B-H線圈的尺寸和形狀如圖8所示，樣品四周相距1mm，是勻場保護層，保護層的材料和疊置方向與樣品相同，勻場保護層作為磁測量樣品的延伸，Ansys-Maxwell的磁場仿真結果表明保護層磁場分布不均勻，但在樣品表面獲得了均勻的磁場，從而避免磁場的邊緣效應。

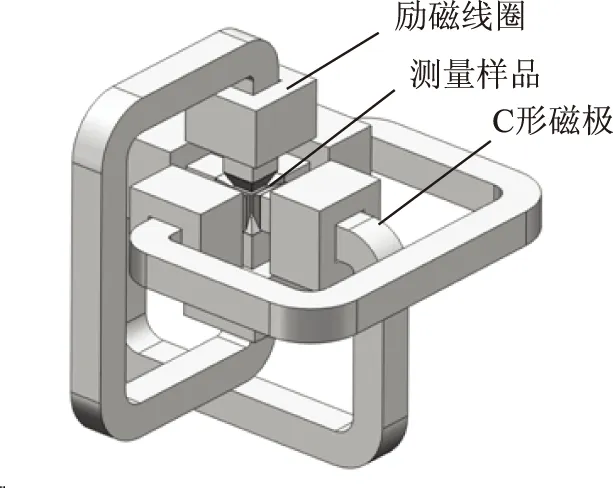
圖7 三維磁特性測量裝置主磁路Fig.7 Three dimensional excitation core structure

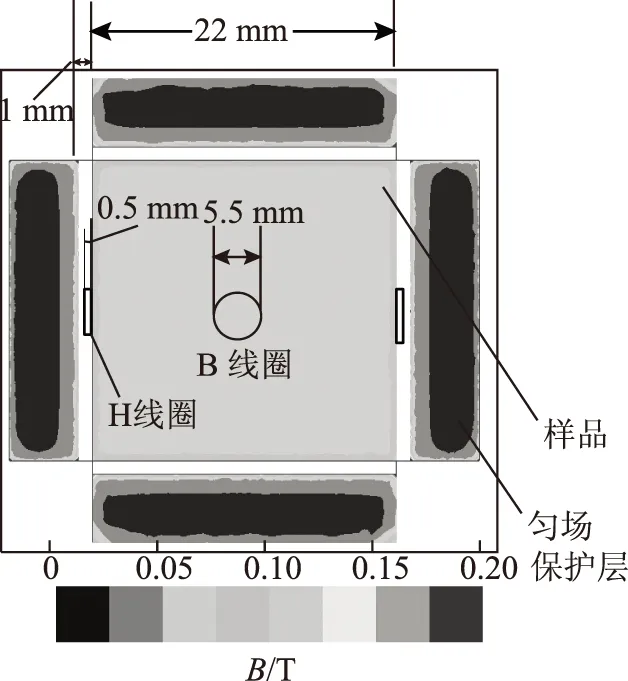
圖8 B-H線圈的尺寸和形狀Fig.8 Size and shape of B-H coil

三維磁測量系統的任意橢圓寬頻勵磁模型為

(26)

式中，Ix、Iy分別為x、y軸勵磁電流；εy為橢圓軌跡軸比。三維磁特性測量系統采用自適應的數字控制算法[24]。以工控機為控制核心，通過多功能采集卡發出三路模擬控制信號，經三路功率放大器和阻抗匹配電路放大獲得大勵磁電流，在測量樣品的內部(SMC或硅鋼疊片)生成交變或旋轉的磁場，從而測量不同勵磁模式下軟磁材料的磁各向異性和損耗特性。

3.2 磁損耗的測量和模型驗證

本文提出的磁滯損耗計算模型同時兼顧交變磁滯損耗和旋轉磁滯損耗。采用三維磁特性測量裝置對無取向鋼片進行多種勵磁模式的損耗測量。首先，通過一組交變磁化實驗和一組圓形磁化實驗辨識損耗模型的參數；其次，利用不同軸比橢圓軌跡下的損耗特性驗證本文損耗模型的有效性。

圖9 對比了四種磁特性測量實驗下的鐵心總損耗，磁滯損耗部分采用本文提出的損耗模型，經典渦流損耗和異常損耗分別采用式(23)和式(24)進行建模分析。根據勵磁模型式(25)，四組實驗磁通密度軌跡分別是εy=0、1、1/2、1/4，軌跡的形狀通過磁場反饋控制算法保證。圖9a是x軸交變損耗實驗結果及兩種模型的預測結果，因為兩種模型的參數都依賴交變勵磁實驗結果，故兩種模型都能夠很好地逼近測量結果。圖9b是圓形旋轉磁化的實驗結果，本文模型的參數使用該組測量數據進行辨識，故兩種模型與實驗結果吻合很好。而基于Steinmetz的方法認為旋轉磁化是兩個方向獨立交變磁化的疊加。鐵磁學的物理磁化過程是當軟磁材料接近飽和時，旋轉磁化的磁性材料磁疇逐漸減少至消失，因此磁滯損耗部分接近于零，故旋轉磁特性實驗損耗低于兩個方向交變的磁特性損耗之和，Steinmetz方法計算的預測旋轉損耗高于測量旋轉損耗，即為模型的主要缺陷。本文模型能夠直接從旋轉磁化角度建模分析，與實驗結果吻合較好。圖9c和圖9d是不同軸比的橢圓激勵的測量結果，混合激勵下的磁疇壁運動行為復雜，既有磁疇壁的平動也包含磁疇壁的轉動，基于Steinmetz的模型僅假設兩個方向獨立的磁疇壁移動，其預測損耗結果低于實際測量結果和本文模型預測結果。

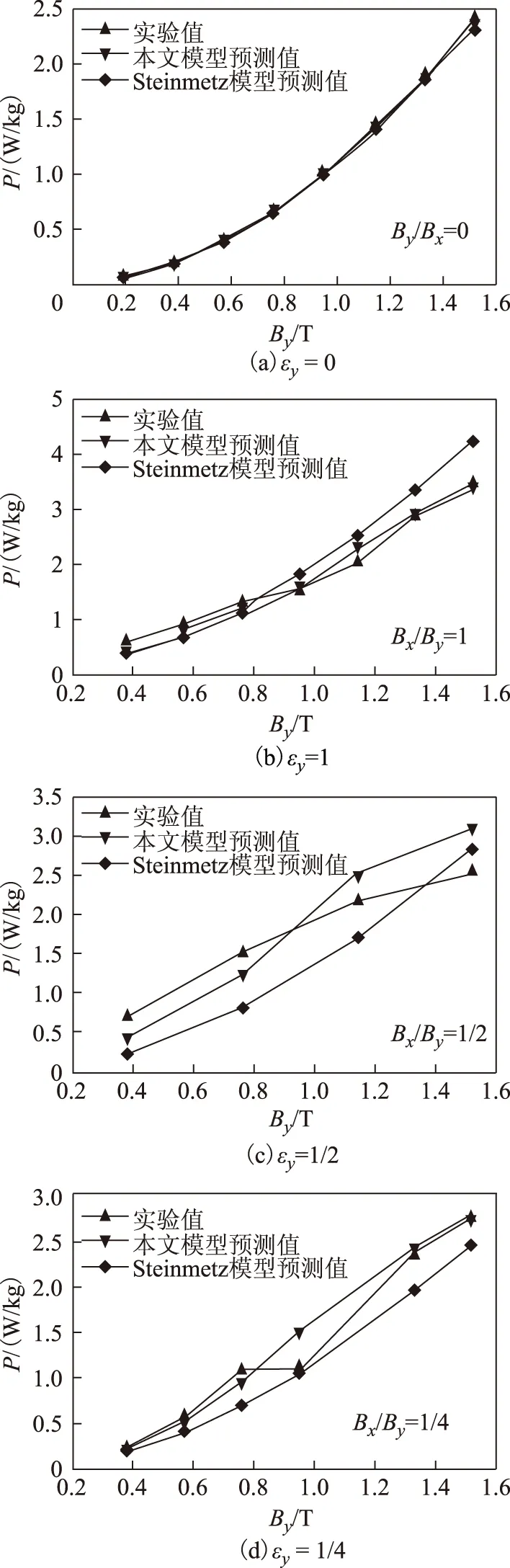
圖9 不同勵磁模式下模型預測值與實驗值對比Fig.9 Comparison of model predictions and experimental values under different excitation modes

綜上，對于四種不同的勵磁模型，本文提出的損耗預測方法與實驗結果誤差較小，尤其在旋轉勵磁下，明顯優于傳統的Steinmetz方法。

4 結論

本文提出一種旋轉磁滯損耗模型，并對SMC材料和無取向硅鋼片進行實驗驗證，詳細闡述了磁滯損耗模型原理及其實現過程。該模型有如下優點：

1)統一了交變損耗和旋轉損耗模型，實現了任意軌跡二維磁滯損耗的計算。

2)損耗模型是基于瞬態實現的，無需存儲全過程的磁化歷史并計算處理，故占用內存少，而且易于集成到電磁有限元分析中。

3)能夠計算過度飽和狀態下旋轉磁滯損耗，此時旋轉磁滯損耗顯著下降，鐵耗主要包括渦流損耗和剩余損耗兩部分，該方法比Steinmetz方法有更高的精度。

[1] 佟文明, 朱曉鋒, 朱龍飛, 等. 不同供電方式對非晶合金永磁同步電機鐵耗的影響[J]. 電工技術學報, 2015, 30(10): 10-18.TongWenming,ZhuXiaofeng,ZhuLongfei,etal.Theimpactofdifferentsupplymodesoncorelossesofamorphousalloypermanentmagnetsynchronousmotor[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(10): 10-18.

[2]BerotttiG.Hysteresisinmagnetismforphysicists,materialsscientists,andengineers[M].NewYork:AcademicPress, 1998.

[3]ReinertJ,BrockmeyerA,DonckerRD.Caculationoflossesinferro-andferromagneticmaterialsbasedonthemodifiedsteinmetzequation[J].IEEETransactionsonIndustryApplications, 2001, 37(4): 1055-1061.

[4]AbdallahJ,SullivanC.Improvedcalculationofcorelosswithnonsinusoidalwaveforms[C]//Thirty-SixthIASAnnualMeeting, 2001, 4: 2203-2210.

[5]IonelD,DellingerSJ,MillerTJE,etal.Onthevariationwithfluxandfrequencyofthecorelosscoefficientsinelectricalmachines[J].IEEETransactionsonIndustryApplications, 2006, 42(3): 658-667.

[6] 趙志剛, 程志光, 劉福貴, 等. 基于漏磁通補償的導磁鋼板直流偏磁雜散損耗特性模擬[J]. 電工技術學報, 2015, 30(8): 38-44.ZhaoZhigang,ChengZhiguang,LiuFugui,etal.ModelingoftheDC-biasedstray-fieldlossofmagneticsteelplatebasedoncompensatorofleakageflux[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(8): 38-44.

[7]ZhuJianguo,RamsdenVS.Improvedformulationsforrotationalcorelossesinrotatingelectricalmachines[J].IEEETransactionsonMagnetics, 1998, 34(4): 2234-2242.

[8] 李丹丹, 劉福貴, 李永建, 等. 一種新的混合矢量磁滯模型磁滯算子定義方法[J]. 電工技術學報, 2014, 29(11): 1-7.LiDandan,LiuFugui,LiYongjian,elal.Anewdefinitionmethodofthehysteroninhybridvectorhysteresismodel[J].TransactionsofChinaElectrotech-nicalSociety, 2014, 29(11): 1-7.

[9] 傅偉, 趙莉華, 梁勇, 等. 多臺變壓器空載合閘勵磁涌流及抑制方案的研究[J]. 電力系統保護與控制, 2015, 43(1): 28-33.FuWei,ZhaoLihua,LiangYong,etal.Studyonno-loadclosinginrushcurrentoftransformergroupandsuppressionmeasures[J].PowerSystemProtectionandControl, 2015, 43(1): 28-33.

[10]姚東曉, 鄧茂軍, 倪傳坤, 等. 變壓器多側勵磁涌流產生機理及對差動快速動作區影響研究[J]. 電力系統保護與控制, 2016, 44(5): 36-41.YaoDongxiao,DengMaojun,NiChuankun,etal.Transformer′smulti-sideinrushcurrentgenerationmechanismanditsinfluenceonthedifferentialprotection′sfastactionzone[J].PowerSystemProtectionandControl, 2016, 44(5): 36-41.

[11]EnokizonoM,SodaN.DirectmagneticlossanalysisbyFEMconsideringvectormagneticproperties[J].IEEETransactionsonMagnetics, 1998, 34(5): 3008-3011.

[12]LinDingsheng,ZhouPing,BergqvistA.Improvedvectorplaymodelandparameteridentificationformagnetichysteresismaterials[J].IEEETransactionsonMagnetics, 2014, 50(2): 357-60.

[13]趙小軍, 崔燦, 李琳, 等. 基于定點諧波平衡法的鐵心磁滯與損耗特性分析[J]. 電工技術學報, 2014, 29(7): 10-18.ZhaoXiaojun,CuiCan,LiLin,etal.Analysisofthehysteresisandlosscharacteristicsinthelaminatedcorebyfixedpointharmonic-balancedmethod[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(7): 10-18.

[14]趙海森, 羅應立, 劉曉芳, 等. 異步電機空載鐵耗分布的時步有限元分析[J]. 中國電機工程學報, 2010, 30(30): 99-106.ZhaoHaisen,LuoYingli,LiuXiaofang,etal.Analysisonno-loadironlossesdistributionofasynchronousmotorswithtime-steppingfiniteelementmethod[J].ProceedingsoftheCSEE, 2010, 30(30): 99-106.

[15]ZhouPing,LinDingsheng,LuChuan,etal.Anewalgorithmtoconsidertheeffectsofcorelosseson3-Dtransientmagneticfields[J].IEEETransactionsonMagnetic, 2014, 50(2): 365-368.

[16]PfutznerH,MulasalihovicE,YamaguchiH,etal.Rotationalmagnetizationintransformercores-areview[J].IEEETransactionsonMagnetics, 2011, 47(11): 4523-4533.

[17]SievertJ.Recentadvancesintheone-andtwo-dimensionalmagneticmeasurementtechniqueforelectricalsheetsteel[J].IEEETransactionsonMagnetics, 1990, 26(3): 2553-2558.

[18]ZurekS,RygalR,SoinskiM.Asymmetryofmagneticpropertiesofconventionalgrain-orientedsteelwithrelationto2Dmeasurement[J].PrzegladElektrotech-niczny, 2009, 85(1): 16-19.

[19]LiYongjian,LinZhiwei,LiuHongxun,etal.Three-dimensionalmagneticpropertiesofsoftmagneticcompositematerialatdifferentfrequencies[J].JournalofAppliedPhysics, 2010, 109(7): 07B503.

[20]張艷麗, 何厚建, 謝德馨, 等. 基于二維磁特性測量的電工鋼片矢量磁滯模型[J]. 中國電機工程學報, 2010, 30(3): 130-135.ZhangYanli,HeHoujian,XieDexin,etal.Vectormagnetichysteresismodelofelectricalsteelsheetsbasedontwo-dimensionalmagneticpropertymeasurement[J].ProceedingsoftheCSEE, 2010, 30(3): 130-135.

[21]LiYongjian,YangQingxin,ZhuJianguo,elal.Designandanalysisofanovel3-Dmagnetizationstructureforlaminatedsiliconsteel[J].IEEETransactionsonMagnetics, 2014, 50(2): 389-392.

[22]KollarP,BircakovaZ,FuzerJetal.PowerlossseparationinFe-basedcompositematerials[J].JournalofMagnetismandMagneticMaterials, 2013, 327(2): 146-150.

[23]DlalaE.Comparisonofmodelsforestimatingmagneticcorelossesinelectricalmachinesusingthefinite-elementmethod[J].IEEETransactionsonMagnetics, 2009, 45(2): 716-725.

[24]ZurekS,MarketosP,MeydanT,etal.Useofnoveladaptivedigitalfeedbackformagneticmeasurementsundercontrolledmagnetizingconditions[J].IEEETransactionsonMagnetics, 2005, 41(11): 4242-4249.

(編輯 張洪霞)

Measurement and Modeling of Rotational Hysteresis Loss ofElectric Soft Magnetic Material

ZhangChanggeng1YangQingxin1,2LiYongjian1

(1.Province-Ministry Joint Key laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China 2. Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy Tianjin Polytechnic University Tianjin 300387 China)

The rotational flux in the core of power transformer and motor causes the inaccuracy efficiency computation of magnetic apparatus. In order to address the problem, this work focuses on magnetic measurement of rotational magnetization and its hysteresis loss modeling. Firstly, the vector hysteresis loss is decomposed into the transverse and radial components which are defined based on rotational loss and alternating loss, respectively. Secondly, the model parameters of soft magnetic composites and non-oriented silicon steel are identified. Their magnetic properties and model parameters are compared and analyzed. Finally, a series of complex excitation magnetization experiments on non-oriented silicon steel are carried out. The measurement results are compared with the predicted values by the model. It shows that the proposed model gives more exact predicted results than the traditional Steinmetz method.

Motor core loss，hysteresis loss，electro-magnetic simulation，rotational loss

國家自然科學基金資助項目(51237005，51507045)。

2016-03-30 改稿日期2016-05-05

TM15

張長庚 男，1985年生，博士研究生，研究方向為工程電磁場與磁技術、三維磁特性測量與建模。

E-mail：chang_geng@sina.com

李永建 男，1978年生，教授，研究方向為工程電磁場與磁技術、三維磁特性測量與建模。

E-mail：liyongjian@hebut.edu.cn(通信作者)