換個角度理解

文︳廖曉嵐

換個角度理解

文︳廖曉嵐

人教版六年級上冊中的數學廣角“數與形”中有如下例題：計算

教材使用的方式是數形結合（如圖所示）。

但圖形中始終存在的那一小塊扇形或那一小段線段不在例題所示的加數之內，也就等于直觀地告訴學生，總和不等于1。無限是不能用直觀表達出來的，學生通過觀察圖形，認為不等于1是非常自然的，甚至許許多多的成年人也會認為不等于1，何況小學生呢？

有人這樣考慮：

=…

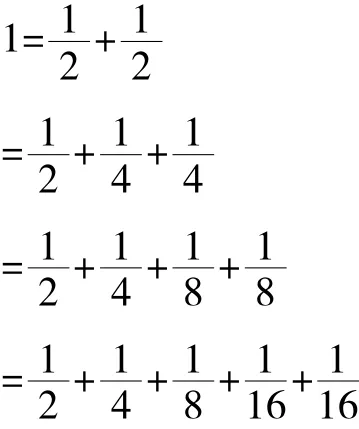
這樣不斷下去，似乎能說明問題。但學生會發現，這里的每一個加法算式的結果都是1，但這里的任何一個加法算式都與題目中的加法算式不同。

當然，我們可以說一句：這是極限。但用一個“極限”對付過去，與其說是解決了問題，不如說是回避或拒絕了討論——憑什么極限就要相等？因此，如何使小學生對例題有一個比較清晰的認識，老師們需要動動腦子。

在教學實踐中，筆者試圖帶領學生換個角度理解問題。

首先，我們要認識，不是隨便無限多個數都可以相加的。比如1+2+3+4+5+6+…就沒有意義。所謂沒有意義，是說你不可能找到一個數，能作為這個加法算式的和。這個不難理解：隨你找個什么數，這個和式都會超過，而且是遠遠地超過你所找的那個數。

第三，我們來確定這個和。或者說，我們要找一個數，使得這個數作為例題中這個無限多個數相加的加法算式的和是合理的。

顯然，這個數不應該大于1。事實上，以上圖中的圓形圖形為例。圓的面積用1表示，則上述加法算式的每一個加數都對應著一個小扇形。容易理解，所有的小扇形都在圓內，都是從圓中分割出來的，沒有重復。它們的和不可能超過圓。

此時，還有兩個可能，或者有一個小于1的數可以作這個和，或者1就是這個和。下面我們來說明，任何一個小于1的數，都是不可能作這個和的。

容易知道，這樣的分析，不僅僅對這兩個數管用，對任何一個小于1的數a，我們都可以確定，這樣不斷地加下去，和總會超過a的。

從上面的討論可以看出，如果我們承認有些情況下，無限多個數也是可以相加的，比如，我們承認是有意義的，那么，我們就必須承認

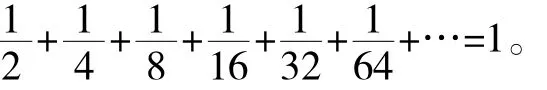
必須說明的是，由于這個算式涉及無限，而無限對于小學生來說，是很難理解的。因此，無論采用什么樣的辦法，我們都不太可能將這個算式的理解變得太簡單。從這個意義上講，也許最好的辦法是：在小學里暫時不討論這個問題。

（作者單位：婁底市第六中學）