構(gòu)建復(fù)習(xí)模式,激活學(xué)生思維
王娟彬
(浙江省樂清外國語學(xué)校)
一、說教材
《萬以內(nèi)加法和減法(二)》是三年級(jí)上冊(cè)第四單元的內(nèi)容。根據(jù)課標(biāo)的要求,筆算加減法限定于三位數(shù)加減三位數(shù),所以這一單元是學(xué)習(xí)整數(shù)加減法的最后階段。本單元是在學(xué)生學(xué)習(xí)了“萬以內(nèi)的加法和減法(一)”的基礎(chǔ)上教學(xué)的。本單元主要是三位數(shù)加減三位數(shù)的計(jì)算教學(xué),其中連續(xù)進(jìn)位加法和連續(xù)退位減法,雖然算理不難理解,但是學(xué)生在練習(xí)時(shí)還是很容易出錯(cuò),是本單元的重點(diǎn),更是難點(diǎn)。
二、說學(xué)情
復(fù)習(xí)課注重梳理,并不是憑空的梳理,要求我們教師要充分了解學(xué)生已經(jīng)知道了什么?還缺什么?基于此,我們?cè)谏蟼€(gè)星期五對(duì)柳市二小三(4)的學(xué)生,專門對(duì)本單元的學(xué)習(xí)內(nèi)容進(jìn)行了前測(cè)調(diào)查。調(diào)查后,我們對(duì)數(shù)據(jù)進(jìn)行了統(tǒng)計(jì)與分析,發(fā)現(xiàn)部分學(xué)生的問題集中在連續(xù)進(jìn)位和連續(xù)退位及估算的應(yīng)用上。
三、說教學(xué)目標(biāo)及重難點(diǎn)
基于以上的教材及學(xué)情分析,我們確定以下教學(xué)目標(biāo):
1.通過回憶整理,構(gòu)建萬以內(nèi)加減法完整的知識(shí)網(wǎng)絡(luò),溝通知識(shí)間的聯(lián)系。
2.通過查漏補(bǔ)缺,讓學(xué)生進(jìn)一步鞏固萬以內(nèi)加減法的計(jì)算法則,提升學(xué)生的計(jì)算能力。
3.在解決問題的過程中,提高應(yīng)用意識(shí),培養(yǎng)數(shù)感,激發(fā)學(xué)生對(duì)數(shù)學(xué)的學(xué)習(xí)興趣。
重難點(diǎn):萬以內(nèi)加減法的連續(xù)進(jìn)位和連續(xù)退位的計(jì)算與應(yīng)用。
四、說教學(xué)方法
我們?cè)谠O(shè)計(jì)本節(jié)復(fù)習(xí)課時(shí),主要圍繞“憶理”“辨析”“講練”三方面,幫助學(xué)生進(jìn)行系統(tǒng)整理,注重知識(shí)的“生長(zhǎng)點(diǎn)”與“延伸點(diǎn)”,把分散的知識(shí)連成線,結(jié)成網(wǎng),組成塊,揭示知識(shí)間的內(nèi)在聯(lián)系,形成新的知識(shí)結(jié)構(gòu),使學(xué)生能更加全面,更加系統(tǒng)地整體理解掌握相關(guān)知識(shí),并在具體的情境中增強(qiáng)應(yīng)用意識(shí)。
五、說教學(xué)程序設(shè)計(jì)
根據(jù)以上的分析與復(fù)習(xí)課的特點(diǎn),我們團(tuán)隊(duì)設(shè)計(jì)以下三大板塊,具體如下:
第一環(huán)節(jié):回憶整理,構(gòu)建網(wǎng)絡(luò)。
為了在課的引入過程中遵循短、平、快的原則,我開門見山直奔主題,讓學(xué)生通過復(fù)習(xí)梳理本單元的知識(shí)要點(diǎn),形成區(qū)域性的知識(shí)結(jié)構(gòu),為今后完善知識(shí)體系做好鋪墊。向?qū)W生說明本節(jié)課的教學(xué)內(nèi)容,讓學(xué)生明確學(xué)習(xí)的方向。通過教材,靜靜地回顧已經(jīng)學(xué)過的7個(gè)例題,整理、歸納出本單元的學(xué)習(xí)內(nèi)容(加法、減法、解決問題)后,我通過提問讓學(xué)生復(fù)習(xí)三位數(shù)加減三位數(shù)的計(jì)算法則,并讓學(xué)生通過觀察,發(fā)現(xiàn)加減法計(jì)算法則之間的聯(lián)系與區(qū)別,梳理出知識(shí)網(wǎng)絡(luò)結(jié)構(gòu)圖,讓學(xué)生的知識(shí)形成一個(gè)完善的體系,也為后續(xù)學(xué)習(xí)做好鋪墊。因?yàn)檫@部分的教學(xué)內(nèi)容,一方面使學(xué)生掌握計(jì)算法則,能熟練計(jì)算,能通過遷移解決更多位數(shù)的加減法計(jì)算;另一方面,也是為進(jìn)一步學(xué)習(xí)小數(shù)加減法和多位數(shù)乘除法打下基礎(chǔ)。
第二環(huán)節(jié):查漏補(bǔ)缺,夯實(shí)基礎(chǔ)。
列式計(jì)算:
215+317= 345+64= 582+419=
469-108= 326-194= 500-167=
“582+419=”和“500-167=”這兩道題做錯(cuò)的學(xué)生較多。一切教學(xué)都要因?qū)W生的需求而設(shè),而不是空空泛談。所以,此環(huán)節(jié)我們?cè)诓槁┑幕A(chǔ)上,通過前測(cè)中發(fā)現(xiàn)的問題,分3步進(jìn)行:第一步,找一找,錯(cuò)在哪?第二步,說一說,要注意什么?第三步,改一改,怎么修正?做到有針對(duì)性地精準(zhǔn)補(bǔ)缺,讓學(xué)生在糾錯(cuò)的過程中復(fù)習(xí)鞏固加減法的計(jì)算法則,通過學(xué)生“眼、口、手”等多種感官的參與,分層次去落實(shí),體現(xiàn)練習(xí)的價(jià)值。通過直觀比較,找出筆算加減法計(jì)算法則間的聯(lián)系與區(qū)別,將知識(shí)系統(tǒng)化,加深了萬以內(nèi)的加、減法的理解和認(rèn)識(shí),突破教學(xué)重難點(diǎn)。
第三環(huán)節(jié):應(yīng)用解決,激活思維。
復(fù)習(xí)課的“練”在我們的教學(xué)中,不同于新授課,更不同于練習(xí)課,復(fù)習(xí)不是舊知識(shí)的簡(jiǎn)單再現(xiàn)和機(jī)械重組,關(guān)鍵是把舊知識(shí)轉(zhuǎn)化,并產(chǎn)生新鮮感,努力做到精準(zhǔn)補(bǔ)缺,學(xué)有所得。根據(jù)三年級(jí)孩子的學(xué)齡特點(diǎn),在練習(xí)的設(shè)計(jì)上注重培養(yǎng)學(xué)生的語言表達(dá)能力及思維的靈活性。
所以,我們安排以下多層梯度的練習(xí)。
1.綜合性練習(xí)。
樂清市外國語學(xué)校“天使杯”葫蘆涂鴉大賽參加的男生有485人,女生有396人,學(xué)校準(zhǔn)備了900個(gè)葫蘆夠嗎?多了多少個(gè)?
本題通過提問“誰能馬上判斷出來,夠嗎?”讓學(xué)生用估算多樣化去判斷夠還是不夠,培養(yǎng)學(xué)生的語言表達(dá)能力與分析問題、解決問題的能力。接著出示問題“多了多少個(gè)?”引導(dǎo)學(xué)生精算。這充分體現(xiàn)了解決問題策略的多樣化,既是練,又是驗(yàn),驗(yàn)練結(jié)合,融為一體,檢測(cè)了學(xué)生知識(shí)掌握的寬度。
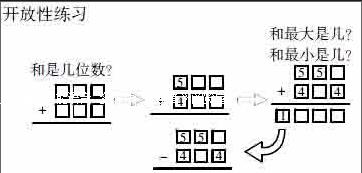
2.開放性練習(xí)。
這個(gè)環(huán)節(jié)是我們對(duì)整個(gè)單元知識(shí)的內(nèi)化與提升。我先讓學(xué)生猜一猜、說一說:在什么情況下三位數(shù)加三位數(shù)和是三位數(shù)?在什么情況下和是四位數(shù)?預(yù)設(shè)學(xué)生只注意百位上的數(shù)有沒有進(jìn)位,如,100+200=300,和是三位數(shù);400+700=1100,和是四位數(shù)。再出示課件,問“那現(xiàn)在呢?和還是三位數(shù)嗎?”讓學(xué)生明白,僅僅只關(guān)注百位上數(shù)是不夠的。因?yàn)榕袛鄡蓚€(gè)三位數(shù)的和是幾位數(shù),不僅要看百位,還要考慮到個(gè)、十、百位之間是否有連續(xù)進(jìn)位的情況。所以通過預(yù)設(shè),追問“百位上5+4=9,為什么說它的和會(huì)是四位數(shù)呢?”通過師生的對(duì)話,生生思維的碰撞,讓不同層次的學(xué)生得到不同的發(fā)展。然后出示,和是四位數(shù)時(shí),和最大及和最小“該怎么思考”。和最大時(shí),我們要考慮0-9中最大的數(shù)字。而和最小時(shí),不僅要考慮小的數(shù)字,還要考慮每?jī)蓚€(gè)數(shù)位之間進(jìn)位與不進(jìn)位的問題,缺一不可。最后從加法遷移至減法,使學(xué)生學(xué)習(xí)得有效,真正做到練有所得,得有所用,用有所依。這樣由易到難,從猜一猜到算一算,整個(gè)環(huán)節(jié)呈螺旋式上升,是整堂課的難點(diǎn)也是亮點(diǎn)。
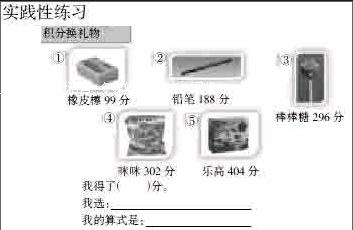
3.實(shí)踐性練習(xí)。
最后,根據(jù)三年級(jí)孩子的學(xué)齡特點(diǎn),我們?cè)O(shè)計(jì)了積分換禮物這一活動(dòng)環(huán)節(jié),就是根據(jù)學(xué)習(xí)單上的得分換取相應(yīng)的禮物。這一環(huán)節(jié)的設(shè)計(jì),主要是為了調(diào)動(dòng)學(xué)生的學(xué)習(xí)參與性與積極性,讓數(shù)學(xué)來源于生活又回歸于生活。
編輯 薄躍華

