低階可約慣量任意符號模式矩陣的刻畫

郝志遠，高玉斌

(中北大學 理學院，太原 030051)

?

低階可約慣量任意符號模式矩陣的刻畫

郝志遠，高玉斌

(中北大學 理學院，太原 030051)

一個n階實矩陣B的慣量是一個非負三元整數組i(B)=(r,s,t)，其中r、s、t分別表示矩陣B的實部為正、負、零的特征值個數(特征值的重數也計算在內)。設A是一個n階符號模式矩陣，A的慣量i(A)是指由全體與A有相同符號模式的實矩陣的慣量構成的集合。若對于任意滿足條件r+s+t=n的非負三元整數組(s,r,t)，都有(s,r,t)∈i(A)，則稱A是慣量任意的。完全刻畫了4、5、6階慣量任意的可約符號模式矩陣。

慣量；慣量任意符號模式；可約符號模式

元素取自集合{+,-,0}的矩陣稱為符號模式矩陣，簡稱符號模式。對于給定的實矩陣B=(bij)，由bij的符號signbij為元素組成的符號模式(signbij)稱為B的符號模式，記為sgnB。用Qn表示全體n階符號模式矩陣所組成的集合。對任意A∈Qn，所有與A有相同符號模式的實矩陣組成的集合{B|B為n階實矩陣，且sgnB=A}稱為由A所決定的定性矩陣類，記為Q(A)。

一個n階符號模式P稱為置換模式，如果它的每一行、每一列都恰好含有1個正元，其余元均為零；一個n階符號模式S稱為符號差模式，如果它是一個對角符號模式，且對角元全非零。

設A與B是兩個n階符號模式，若存在一個n階置換模式P使得A=PTBP，則稱A與B置換相似；若存在一個n階符號差模式S使得A=SBS，則稱A與B符號差相似。如果A可以由B經過轉置、取負、置換相似、符號差相似得到，則稱A與B是等價的。

一個n階實矩陣B的慣量是指非負三元整數組i(B)=(r,s,t)，其中r、s、t分別表示矩陣B的實部為正、負、零的特征值個數(特征值的重數也計算在內)。一個n階符號模式A的慣量是指非負三元整數組的集合i(A)={i(B)|B∈Q(A)}。

文獻[1]最早提出了譜任意和慣量任意符號模式矩陣的問題。文獻[2]給出了第1個慣量任意的n階符號模式。文獻[3]給出了第1個譜任意(從而也是慣量任意)的n階符號模式。隨后人們陸續找到一些譜任意(慣量任意的)符號模式[4-8]，但至今沒有一個好的方法來刻畫慣量任意符號模式。文獻[9]提出一種刻畫慣量任意性的新方法：慣量臨界集的概念，并給出了2階、3階零-非零模式的極小慣量臨界集，但刻畫慣量任意符號模式仍然是一個困難問題，特別是對于可約符號模式的慣量任意性，目前僅有少量文獻進行研究[10]。本文將對4、5、6階可約慣量任意符號模式進行刻畫。

1 預備知識

定義1 設A為n階方陣，若存在一個n階置換矩陣P，使得

其中A11和A22分別為k、l階非空方陣，且滿足k+l=n，則稱A可約，否則稱A不可約。

定義2 設X與Y均為整數集，則稱集合{x+y:x∈X,y∈Y}為X與Y的和集，記為X+Y。

引理 1[10]設A、B為兩個符號模式矩陣，則i(A⊕B)=i(A)+i(B)。

引理 2[9]設A為一個2階不可約符號模式，則以下條件是等價的：

①A為譜任意的；

②A為慣量任意的；

③A蘊含慣量(0,0,2)和(2,0,0)或(0,0,2)和(0,2,0)；

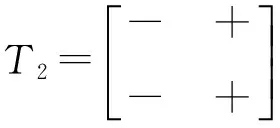
引理3[9]設A為一個3階不可約符號模式，則以下條件是等價的：

①A為譜任意的；

②A為慣量任意的；

③A蘊含慣量(0,0,3)和(3,0,0)，或(0,0,3)和(0,3,0)；

④A等價于如下4個符號模式之一或者它們的某一個母模式：

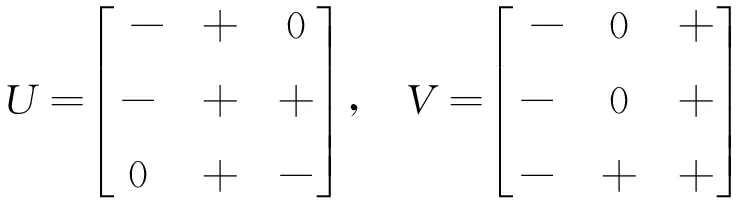
2 4階可約慣量任意符號模式

定理1 設A是一個4階可約符號模式，則A是慣量任意的，當且僅當A等價于如下模式：

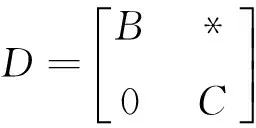
其中B、C均為2階慣量任意的不可約符號模式，即B、C均等價于引理2 ④中的符號模式T2。

充分性：

設B、C均為慣量任意的，則i(B)=i(C)={(2,0,0),(0,2,0),(1,1,0),(1,0,1),(0,1,1),(0,0,2)},由引理1知：i(D)=i(B⊕C),i(B⊕C)=i(B)+i(C)={(4,0,0),(0,4,0),(3,1,0),(1,3,0),(2,2,0),(3,0,1),(0,3,1),(2,1,1),(1,2,1),(2,0,2),(1,1,2),(0,2,2),(1,0,3),(0,1,3),(0,0,4)},故D是慣量任意的，從而A是慣量任意的。充分性得證。

必要性：

設A是慣量任意的，則(4,0,0),(0,4,0),(0,0,4)∈i(A)。由引理.1知：i(A)=i(D)=i(B⊕C)=i(B)+i(C),且注意慣量(4,0,0)、(0,4,0)、(0,0,4)中每個只能由下列慣量之和取得：

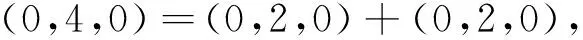
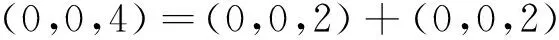
故B、C均蘊含慣量(2,0,0)、(0,2,0)、(0,0,2),由引理2知：B,C均為慣量任意的，必要性得證。

定理1證明完畢。

推論1 設A為4階可約慣量任意符號模式，則A至少含有8個非零元。

3 5階可約慣量任意符號模式

定理2 設A是一個5階可約符號模式，則A是慣量任意的，當且僅當A等價于如下模式：

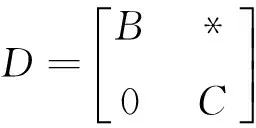
其中B、C分別為2階、3階不可約慣量任意符號模式，即B等價于引理2 ④中的符號模式T2，C等價于引理3 ④中4個符號模式D3×3、D3×2、U、Vs之一或它們某一個的母模式。

充分性：

設B,C均為慣量任意的，則i(B)={(2,0,0),(0,2,0),(1,1,0),(1,0,1),(0,1,1),(0,0,2)},i(C)={(3,0,0),(0,3,0),(2,1,0),(1,2,0),(2,0,1),(1,0,2),(1,1,1),(0,1,2),(0,2,1),(0,0,3)}，由引理1知：

i(D)=i(B⊕C)=i(B)+i(C)={(5,0,0),(0,5,0),(4,1,0),(1,4,0),(3,2,0),(2,3,0),(4,0,1),(0,4,1),(3,1,1),(1,3,1),(2,2,1),(3,0,2),(0,3,2),(2,1,2),(1,2,2),(2,0,3),(0,2,3),(1,1,3),(1,0,4),(0,1,4),(0,0,5)}

故D是慣量任意的，從而A是慣量任意的。充分性得證。

必要性：

設A是慣量任意的，則(5,0,0)、(0,5,0)、(0,0,5)∈i(A)。由引理1知：i(A)=i(D)=i(B⊕C)=i(B)+i(C),且注意到慣量(5,0,0)、(0,5,0)、(0,0,5)中每個只能由下列慣量之和取得：

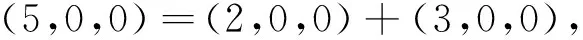
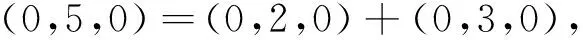
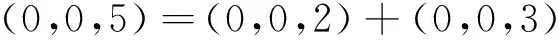
故B蘊含慣量(2,0,0)、(0,2,0)、(0,0,2)，C蘊含慣量(3,0,0)、(0,3,0)、(0,0,3)。由引理2及3知：B、C均為慣量任意的，必要性得證。

定理2證畢。

推論2 設A是一個5階可約慣量任意符號模式，則A至少含有10個非零元。

4 6階可約慣量任意符號模式

注意到對于一個6階慣量任意的可約符號模式，它的不可約塊可以為3個2階、2個3階或1個2階和1個4階，下面分情況進行討論。

定理3 設A是一個6階可約符號模式，其不可約塊為3個2階符號模式，則A是慣量任意的，當且僅當A等價于如下模式：

其中B、C、F均為2階不可約慣量任意符號模式，即B、C、F均等價于引理2 ④中的符號模式T2。

充分性：

設B、C、F均為慣量任意的，則i(B)=i(C)=i(F)={(2,0,0),(0,2,0),(1,1,0),(1,0,1),(0,1,1),(0,0,2)}。

由引理1知：i(D)=i(B⊕C⊕F)=i(B)+i(C)+i(F)={(6,0,0),(0,6,0),(5,1,0),(1,5,0),(4,2,0),(2,4,0),(3,3,0),(5,0,1),(0,5,1),(4,1,1),(1,4,1),(3,2,1),(2,3,1),(4,0,2),(0,4,2),(3,1,2),(1,3,2),(2,2,2),(3,0,3),(0,3,3),(2,1,3),(1,2,3),(2,0,4),(0,2,4),(1,1,4),(1,0,5),(0,1,5),(0,0,6)}。故D是慣量任意的，從而A是慣量任意的。充分性得證。

必要性：

設A是慣量任意的，則(6,0,0),(0,6,0),(0,0,6)∈i(A)。由引理1知：i(A)=i(D)=i(B⊕C⊕F)=i(B)+i(C)+i(F),且注意到慣量(6,0,0),(0,6,0),(0,0,6)中每個只能由下列慣量之和取得：

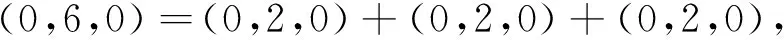
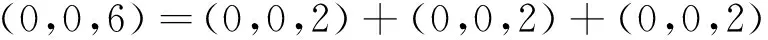
B、C、F蘊含慣量(0,0,2),(2,0,0),(0,2,0),因此根據引理2，它們都是慣量任意的，必要性得證。

定理3證明完畢。

定理4 設A是一個6階可約符號模式，且其不可約塊為2個3階符號模式，則A是慣量任意的，當且僅當A等價于如下模式：

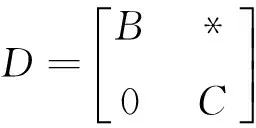
其中B、C均為3階不可約慣量任意符號模式，即B、C均等價于引理3 ④中4個符號模式D3×3、D3×2、U、Vs之一或它們某一個的母模式。

充分性：

設B、C均為慣量任意的，則i(B)=i(C)={(3,0,0),(0,3,0),(2,1,0),(1,2,0),(2,0,1),(0,2,1),(1,1,1),(1,0,2),(0,1,2),(0,0,3)}。

由引理1知i(D)=i(B⊕C)=i(B)+i(C)= {(6,0,0),(0,6,0),(5,1,0),(1,5,0),(4,2,0),(2,4,0),(3,3,0),(5,0,1),(0,5,1),(4,1,1),(1,4,1),(3,2,1),(2,3,1),(4,0,2),(0,4,2),(3,1,2),(1,3,2),(2,2,2),(3,0,3),(0,3,3),(2,1,3),(1,2,3),(2,0,4),(0,2,4),(1,1,4),(1,0,5),(0,1,5),(0,0,6)}。故D是慣量任意的，從而A是慣量任意的。充分性得證。

必要性：

設A是慣量任意的，則(6,0,0),(0,6,0),(0,0,6)∈i(A)。由引理1知i(A)=i(D)=i(B⊕C)=i(B)+i(C),且慣量(6,0,0)、(0,6,0)、(0,0,6)中每個只能由下列慣量之和取得：

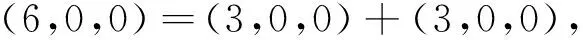
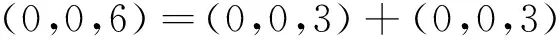
故B、C蘊含慣量(3,0,0),(0,3,0),(0,0,3)，因此根據引理3，它們都是慣量任意的，必要性得證。

定理4證明完畢。

推論3 設A是一個6階可約符號模式，若其不可約塊為3個2階符號模式或兩個3階符號模式，則A至少含有12個非零元。

現在討論不可約塊是一個2階和一個4階的6階可約符號模式A的慣量任意性。此時，A等價于

其中B、M分別為2階、4階不可約符號模式。

注意到A蘊含的慣量(6,0,0),(0,6,0),(0,0,6)中每個只能由下列慣量之和取得：

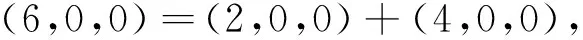
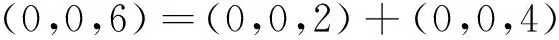
故當A是慣量任意時，B蘊含慣量(2,0,0)、(0,2,0)、(0,0,2)，M蘊含慣量(4,0,0)、(0,4,0)、(0,0,4)。由引理2知：當A是慣量任意時，B一定是慣量任意的。例1表明：M可以是非慣量任意的。

例1[10]設

則B是慣量任意的，注意到(0,1,3)、(0,3,1)、(2,1,1)?i(M)，但A=B⊕M是慣量任意符號模式。

下面定理將給出這樣的6階可約符號模式A為慣量任意的一個充分必要條件。

定理5 設A是一個6階可約符號模式，其不可約塊為1個2階和1個4階不可約符號模式，則A是慣量任意的當且僅當A等價于如下模式：

其中B是2階不可約慣量任意符號模式(即等價于引理2 ④中的符號模式T2)，M滿足以下條件：

①M蘊含慣量(4,0,0)、(0,4,0)、(0,0,4)；

②M至少蘊含慣量(3,1,0)、(1,3,0)、(2,2,0)中之一；

③M至少蘊含慣量(3,0,1)、(1,0,3)、(2,0,2)中之一；

④M至少蘊含慣量(0,3,1)、(0,2,2)、(0,1,3)中之一；

⑤M至少蘊含慣量(3,1,0)、(2,2,0)、(3,0,1)、(2,1,1)、(1,2,1)中之一；

⑥M至少蘊含慣量(1,3,0)、(2,2,0)、(0,3,1)、(2,1,1)、(1,2,1)中之一；

⑦M至少蘊含慣量(3,1,0)、(3,0,1)、(2,1,1)、(2,0,2),(1,1,2)中之一；

⑧M至少蘊含慣量(1,3,0)、(0,3,1)、(1,2,1)、(0,2,2),(1,1,2)中之一；

⑨M至少蘊含慣量(2,1,1)、(2,0,2)、(1,1,2)、(1,0,3),(0,1,3)中之一；

⑩M至少蘊含慣量(1,2,1)、(0,2,2)、(1,1,2)、(1,0,3),(0,1,3)中之一；

證明 設A等價于

其中B、M分別為2階、4階不可約符號模式。

充分性：

設B是慣量任意的，且M滿足定理的11個條件，則i(B)={(2,0,0),(0,2,0),(1,1,0),(1,0,1),(0,1,1),(0,0,2)}。所以，由條件①可得D蘊含如下所有慣量：

(6,0,0),(4,2,0),(5,1,0),(5,0,1),(4,1,1),(4,0,2),(2,4,0),(0,6,0),(1,5,0),(1,4,1),(0,5,1),(0,4,2),(2,0,4),(0,2,4),(1,1,4),(1,0,5),(0,1,5),(0,0,6)

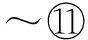
(3,3,0),(3,0,3),(0,3,3),(3,2,1),(2,3,1),(3,1,2),(1,3,2),(2,1,3),(1,2,3),(2,2,2)

所以，D是慣量任意的，從而A是慣量任意的。充分性得證。

必要性：

設A是慣量任意的，則：

i(A)=i(D)={(6,0,0),(4,2,0),(5,1,0),(5,0,1),(4,1,1),(4,0,2)，(2,4,0),(0,6,0),(1,5,0),(1,4,1),(0,5,1),(0,4,2),(2,0,4),(0,2,4),(1,1,4),(1,0,5),(0,1,5),(0,0,6),(3,3,0),(3,0,3),(0,3,3),(3,2,1),(2,3,1),(3,1,2),(1,3,2),(2,1,3),(1,2,3),(2,2,2)}

注意到，慣量(6,0,0)、(0,6,0)、(0,0,6)中每個只能由下列慣量之和取得：

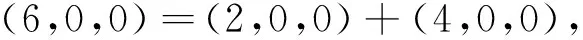
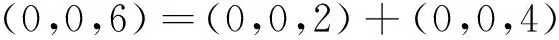
故M蘊含慣量(4,0,0)、(0,4,0)、(0,0,4)，條件①成立。又慣量(3,3,0)只能由下列3種慣量之和取得：

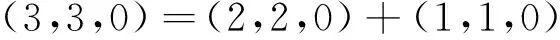
定理5證明完畢。

[1] DREW J H,JOHNSON C R,OLESKY D D.Spectrally arbitrary patterns[J].Linear Algebra and its Applications,2000,308(1/2/3):121-137.

[2] GAO Y,SHAO Y.Inertially arbitrary patterns[J].Linear and Multilinear Algebra,2001,49(2):161-168.

[3] MCDONALD J J,OLESKY D D,TSATSOMEROS M J,et al.On the spectra of striped sign patterns[J].Linear and Multilinear Algebra,2003,51(1):39-48.

[4] BRITZ T,MCDONALD J J,OLESKY D D,et al.Minimal spectrally arbitrary sign patterns[J].SIAM Journal on Matrix Analysis and Applications,2004,26(1):257-271.

[5] KIM I J,OLESKY D D,VAN D D P.Inertially arbitrary sign patterns with no nilpotent realization[J].Linear Algebra and its Applications,2007,421(2/3):264-283.

[6] MIAO Z,LI J.Inertially arbitrary (2r-1)-diagonal sign patterns[J].Linear algebra and its applications,2002,357(1/2/3):133-141.

[7] KIM I J,MCDONALD J J,OLESKY D D,et al.Inertias of zero-nonzero patterns[J].Linear and Multilinear Algebra,2007,55(3):229-238.

[8] DREW J H,JOHNSON C R,OLESKY D D.Spectrally arbitrary patterns[J].Linear Algebra and its Applications,2000,308(1/2/3):121-137.

[9] KIM I J,OLESKY D D,VAN D D P.Critical sets of inertias for matrix patterns[J].Linear and Multilinear Algebra,2009,57(3):293-306.

[10]CAVERS M S.On reducible matrix patterns[J].Linear and Multilinear Algebra,2010,58(2):257-267.

(責任編輯 陳 艷)

Characterization for Lower Order Reducible Inertially Arbitrary Sign Patterns

HAO Zhi-yuan, GAO Yu-bin

(School of Science, North University of China, Taiyuan 030051, China)

The inertia of a real matrixBof ordernis the triple of nonnegative integersi(B)=(r,s,t) in whichr,s,tare the numbers of its eigenvalues (counting multiplicities) with positive, negative and zero real parts respectively. The inertia of ann×nsign pattern matrixAis the set of {i(A)|i(A)=i(B),sgnB=A}. Ann×nsign pattern matrixAis an inertially arbitrary pattern if (r,s,t)∈i(A) for every nonnegative triple (r,s,t) withr+s+t=n. This article characterizes the reducible inertially arbitrary sign patterns of orders 4, 5 and 6.

inertia; inertially arbitrary sign pattern; reducible sign pattern

2016-12-15 基金項目：國家自然科學基金資助項目(11071227)；山西省回國人員科研資助項目(12-070)

郝志遠(1990—)，男，碩士研究生，主要從事組合數學研究，E-mail:1065711678@qq.com；通訊作者 高玉斌(1962—)，男，博士，教授，博士生導師，主要從事組合數學研究，E-mail:ybgao@nuc.edu.cn。

郝志遠，高玉斌.低階可約慣量任意符號模式矩陣的刻畫[J].重慶理工大學學報(自然科學)，2017(5):186-191.

format：HAO Zhi-yuan, GAO Yu-bin.Characterization for Lower Order Reducible Inertially Arbitrary Sign Patterns[J].Journal of Chongqing University of Technology(Natural Science)，2017(5):186-191.

10.3969/j.issn.1674-8425(z).2017.05.031

O157

A

1674-8425(2017)05-0186-06