數學必備品格的要素之“數學理性”

劉娟娟

【理論篇】

數學必備品格的要素之“數學理性”

劉娟娟

文章探討了理性和數學理性的內涵，從數學理性形成規律、數學核心素養培育、對數學學科的理解三個層面分析了培養學生數學理性的必要性，最后提出培養學生數學理性的策略：一是要重視數學抽象能力的培養；二是要注重數學推理能力的培養；三是要注重質疑能力的培養。

數學理性；客觀；抽象；精確；定量

數學作為人類文化的一部分，不僅包括數學的知識、方法，還包括數學的語言、思想、精神等。特別是在自然科學和社會科學融合發展中，數學將其理性精神發揮得淋漓盡致，不僅為人類的發展提供了理性的思維方式和工具，也為人類思想發展指引了方向。那么如何理解理性和數學理性，如何培養學生的數學理性是數學教育工作者應該面對的問題，本文就是在這方面做的一些思考。

一、理性和數學理性

（一）數學是一種理性

理性是現代文化中的高頻詞，詞典中的“理性”有兩個意思：一是指判斷、推理等活動（跟“感性”相對）；二是指從理智上控制行為的能力。不同的文化孕育著不同風格的理性，人類對理性的使用與其所處的社會歷史環境有著密切的關聯，不是絕對的，而是歷史的，是隨著歷史的發展和變遷不斷變化的。但就其共性而言，一般認為理性是人類精神活動的一種形式，是一種人類特有的思想活動，既包括概念、判斷和推理，也包括質疑、反駁和辯護，不僅關涉到知識的獲得，而且關涉到行為目的的正當性與辯護的合理性。所以，理性又可以叫作理性精神，或是理性思想。

數學恰恰具備了理性的上述特征，數學經典名著《什么是數學》中寫道：“數學，作為人類智慧的一種表達形式，反映生動活潑的意念、深入細致的思考，以及完美和諧的愿望，它的基礎是邏輯和直覺，分析和推進，共性與個性。”可見，數學是人類的一種精神活動，包含了判斷、推理等活動。因此，數學是一種理性。

（二）數學理性的內涵

數學理性起源于古代希臘，是人類重視從數量和邏輯運演的角度來探索客觀世界的規律，從而對世界進行定量、精確、邏輯的描述方式。具體來說，數學理性的內涵可以從以下四個方面理解：

1.堅持客觀理智的立場。

數學研究的對象不是客觀世界中真實存在的，而是人類抽象思維的產物。但是在研究中，我們還是采取純客觀的立場，把它看作一種不依賴人類的獨立存在，并通過嚴格的邏輯分析去揭示其內在性質和關系。比如三角形的概念是人類的創造，但是研究其內角和的規律時，依然要從客觀的角度去思考，并討論在不同幾何體系背景下的內角和的差異。

2.注重精確、定量的思維方式。

數學理性的“數學味”就體現在它的“精確”“定量”上，而不應是含糊的、直覺的。這既是科學研究的基本方法，也是科學研究的基本目標，即揭示自然界中的數學規律。以“圓周率”為例，從《周髀算經》中的“周三徑一”，到“徽率 3.1416”，再到祖沖之算出圓周率在3.1415926到3.1415927之間，再到1882年德國數學家林德曼不僅證明了π是一個無理數，而且還是一個超越數……都體現出人類對圓周長與直徑關系精確、定量的追求。小學數學課程內容中安排的探索規律也都是期望學生能從數量上發現規律、總結規律、應用規律。

3.要有批判的精神和開放的頭腦。

批判的精神讓我們時刻提醒自己不要淪為權威主義者，而要重視用可靠的論證來判斷真理，正如亞里士多德的名言所述“吾愛吾師，但吾更愛真理”。開放的頭腦是對批判精神的重要補充，這就是要以真理為目標，在探索真理的過程中，保持頭腦的開放性，不斷接納別人的想法，修正自己的觀點。美國數學家喬治·波利亞稱前者是“理智上的勇氣”，稱后者為“理智上的誠實”。

4.保持抽象、超驗的思維取向。

自然科學研究的目的是為了超越直觀經驗，通過抽象思維達到對事物本質普遍規律的認識，只要保持這種抽象、超驗的思維取向，才能將特殊轉化為一般，感性上升為理性，透過現象看到本質，將眼前的現實轉化為未來的永恒。

二、培養學生數學理性的必要性

美國數學家M·克萊因說：“數學是一種精神，一種理性精神。正是這種精神激發、促進、鼓舞并驅使人類的思維得以運用到最完善的程度，也正是這種精神，試圖決定性地影響人類的物質、道德和社會生活；試圖回答有關人類自身存在提出的問題；努力去理解和控制自然；盡力去探求已經獲得知識的最深刻的和最完善的內涵。”由此可見，數學作為一種理性精神有著重要的價值和作用，那么培養學生的數學理性十分必要。

（一）從數學理性形成的規律來看

數學理性作為一種需要借助數學概念、數量關系進行推理，進而發現事物本質的認識活動，其形成過程必然與個體對相關數學概念系統的掌握程度，推理規則的熟悉程度以及推理經驗的多寡等有著密切的聯系。學生的數學理性不是天生具備的，在生活中有意識地培養數學理性的機會也很少，因此特別需要教師在數學課堂中重視數學理性的培養，這樣才能使其由弱變強，如若不加重視和強化，數學理性也是會減弱和喪失的。

追求數學理性精神有助于學生充分感受人類理性思維的力量，增強其利用推理獲得成功的信念和面對失敗的承受力，提高思維的抽象性、概括性、嚴謹性、深刻性和批判性等品格，養成心平氣和地待人、簡明扼要地說話、抓住本質看問題、從全局考慮事情等品格。

（二）從數學核心素養的培育上看

2016年發布的 《面向未來：21世紀核心素養教育的全球經驗》研究報告，讓核心素養被越來越多的人所關注。對照核心素養的界定，數學核心素養被認為是“學生應具備的適應終身發展和社會發展需要的必備數學品格和關鍵數學能力”。人們對“關鍵能力”的關注較多，需要特別關注的是，高中數學課程標準修訂組專家根據教育部的要求，提出高中數學核心素養包括：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析，但是其中聚焦的都是關鍵能力層面的。

南京師范大學喻平教授指出：“各學科核心素養成分的確定多是由一批專家綜合各方面意見討論而定，這種基于思辨的研究，基于專家的理論見識，有不可替代的作用，但是這種小群體的價值信念也可能會出現以偏概全的缺陷。對學科核心素養成分的研究，應當采用思辨提出框架、實證加以驗證的方法。”他通過因子分析和聚類分析，得到數學核心素養除了數學抽象、運算能力、推理能力、建模與數據處理（或數學建模、數據處理）、空間能力外，還應包括問題解決能力和數學文化品格。其中數學文化品格包括理解數學文化傳承、數學思想方法、數學理性精神、數學審美等。

（三）從對數學學科的理解上看

盡管數學被人們看作是由理論、方法、問題和符號等多種成分組成的多元復合體，但是有一點我們不可忽視，那就是“數學是一種完全的可靠的知識，是一種科學，它給人以理性”。愛因斯坦在談到數學時說：“為什么數學相比其他科學受到特殊的尊重，一個理由是它的命題是絕對可靠的和無可爭辯的，而其他一切科學的命題在某種程度上都是可爭辯的，并且經常處于會被新發現的事實推翻的危險之中。”“數學之所以有這么高的聲譽，還有另一個理由，那就是數學給予精密自然科學以某種程度的可靠性，沒有數學，這些科學是達不到這種可靠性的。”培養學生的數學理性，可以增強學生對數學“精確性”“定量性”“抽象性”“邏輯性”等的理解，可以幫助學生更好地把握數學的本質。

三、數學理性的培養策略

學生數學理性的形成是一個長期積累的過程，對學生數學理性的培養需要教師提高自身對數學理性的認識和理解，才能在平時的教學中對學生進行有針對性的培養。

1.要重視數學抽象能力的培養。

數學抽象就是從數量關系和空間形式的角度抽取事物的本質特征，從而提煉數學概念、構建數學模型，創新數學方法。在教學中重視數學抽象意味著幫助學生從客觀的角度來看待研究對象，從定量化、精確化等角度把握事物的本質特征。

例如：在蘇教版三上《間隔排列》的教學中，教師通過介紹間隔排列的概念，讓學生明確該排列由兩種物體構成，再通過讓學生自由創造間隔排列的實例和排隊活動，進一步感受其中的數據特點，接著通過出示判斷“下面兩種物體能不能組成間隔排列？”“4支鉛筆，4塊橡皮”“5朵藍花，4朵紅花”“4 棵柳樹，7 棵楊樹”“100個鍵盤，101個鼠標”，讓學生進一步感受能間隔排列的兩種物體的數據規律，之后再對能夠間隔排列的兩組數據進行分類研究，最終得到“能間隔排列的兩種物體，如果兩端相同，它們的數量相差1；如果兩端不同，它們的數量正好相等”。整個教學始終突出對數量的感知，使得數量關系的抽象水到渠成，凸顯數學理性。

2.要注重數學推理能力的培養。

自新課程改革以來，數學教學特別倡導讓學生采用“觀察和實驗”的方法進行學習，但是如果學生始終停留在“實驗和歸納”的水平上是不夠的，不能真正獲得數學理性。因為數學理性強調有條理、有依據地探究問題和解決問題，因此教學中需要重視“驗證和推理”。

例如：在探索乘法分配律時，通過讓學生觀察大量實例得到規律后，還可以讓學生看看能否找到反例，如果找不到反例，也就增強了規律的正確性；另一方面可以通過數形結合的方式來驗證，如圖1所示。

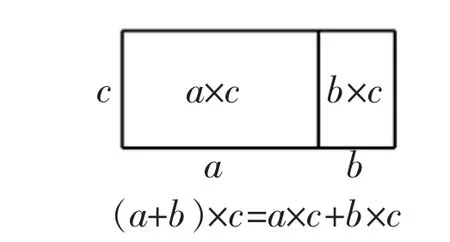
（圖 1）

3.要注重質疑能力的培養。

追求數學理性，要學會對數據的真實性、精確性、可靠性、正確性等進行質疑，對推理過程的邏輯性、嚴謹性進行反思，這樣才能不斷地提升數學理性水平。在教學中要培養學生的質疑能力，首先要營造民主平等的氛圍；其次要重視培養學生對數學的感覺；再次就是要注重質疑方法的引導，比如可以從問題條件的充分性，問題解決過程的邏輯性，問題答案的正確性等角度進行質疑；最后還要對質疑進行合理的評價。

最后，值得一提的是，要辯證地看待數學理性。一方面不要走到純粹主義數學的老路上，肯定數學理性重要性的同時，也要清楚地認識到，數學理性不是唯一的理性形式，也要重視其他的理性形式，如中國古代數學偏重實用主義的理性精神也是需要我們學習的。另一方面數學理性也有其局限性，數學理性并不能代表數學的全部。

［1］石中英.教育哲學導論［M］.北京：北京師范大學出版社，2004.

［2］鄭毓信，王憲昌，蔡仲.數學文化學［M］.成都：四川教育出版社，2000.

［3］R·柯朗，H·羅賓.什么是數學：對思想和方法的基本研究［M］.左平，張飴慈，譯.上海：復旦大學出版社，2012.

［4］喻平.數學學科核心素養要素析取的實證研究［J］.數學教育學報，2016（6）：1-6.

［5］方延明.數學文化導論［M］.南京：南京大學出版社，1999.

［6］周衛東.關注必備品格，提升核心素養［J］.教育視界，2016（24）：7-9.

［7］鄭毓信.數學教育視角下的“核心素養”［J］.數學教育學報，2016（3）：1-5.

G623.5

A

1005-6009（2017）33-0007-03

劉娟娟，南京曉莊學院教師教育學院（南京，211171）副教授，美國佛羅里達大學教育學院訪問學者，研究方向：小學數學課程與教學、小學數學教師教育研究。