多類應急資源配置的魯棒選址-路徑優化

彭 春，李金林，王珊珊，冉 倫

(北京理工大學管理與經濟學院，北京 100081)

?

多類應急資源配置的魯棒選址-路徑優化

彭 春，李金林，王珊珊，冉 倫

(北京理工大學管理與經濟學院，北京 100081)

本文基于應急資源配置的災前預防準備和災后的響應分配，在多類應急資源配置選址-路徑優化名義模型的基礎上，考慮多類應急資源成本的不確定性，引入兩類不確定集合(box 和ellipsoid)刻畫該不確定性，分別建立多類應急資源魯棒選址-路徑優化模型，運用魯棒優化方法，將其轉化為易求解處理的魯棒等價模型，并通過CPLEX和GAMS混合編程算法求解。最后，本文對我國四川北部和西部自然災害多發區的19個縣市進行應急資源優化配置分析，確定應急資源臨時供應點的最優選址布局、應急資源的分配路徑，同時考慮擾動比例的靈敏度分析，驗證模型的可行性和有效性。結果表明在其他條件相同的情況下，ellipsoid不確定集合下的魯棒模型較保守，配置的總成本較高，因此決策者可以根據自己的風險厭惡程度選擇不確定水平參數的值，確定應急資源的配置方案，進而為相關應急救災部門在災前預防準備工作提供決策支持。

應急資源；選址-路徑；成本不確定性；魯棒優化；不確定集合

1 引言

我國是世界上自然災害嚴重的國家之一，災害種類多，發生頻率高，災害損失嚴重。2009年國務院新聞辦公室發布的《中國的減災行動》白皮書中重點提出，建立完善的減災工作管理體制和運行機制，災害監測預警、防災備災、應急處置、災害救助、恢復重建能力大幅提升，公民的減災意識顯著增強、減災技能顯著提高，人員傷亡和自然災害造成的直接經濟損失明顯減少[1]。在應急災害管理中，最有效的方式是盡力做好災害發生前的預防和準備工作，以及災后的第一時間應急救災網絡的響應工作，盡可能的降低災后的損失和影響，具有重要意義。應急資源的配置問題，涵蓋災害發生前的應急物資的配置問題(選址和儲備)和災害發生后的資源分配問題(分配、路徑)，具體包括臨時救災點的選址、應急資源運輸的路徑和分配，力圖解決應急資源的供應地點應該選在何處，每個供應地點應配置多少資源，應急資源的運輸路線及最優的調度資源數量，使得應急資源的需求被滿足，總成本最小。

Altay和Green[2]通過分析之前已有成果，回顧OR/MS方法在應急災害管理中的應用，并指出了幾個未來研究方向，其中之一為如何度量應急管理過程中的不確定性；Galindo和Batta[3]在Altay, Green基礎上，對近年來OR/MS方法在應急管理方面的文獻進行綜述，同時指出了新的方向，包括利用新的方法(如魯棒優化)來建立優化模型。Mete 和Zabinsk[4]考慮不同的災害類型及級別，建立兩階段應急醫療服務站選址布局的隨機優化模型，考慮選址和資源的分配路徑優化，并利用情景分析求解；葛洪磊和劉南[5]提出基于區域災害系統理論來構建復雜災害情景描述突發事件的復雜性和高度不確定性，建立兩階段隨機規劃模型，進行應急設施的定位決策、應急資源的庫存決策和不同災害情景下應急資源分配預案的制定。

早期對于應急資源配置的研究均假設應急資源的需求、成本或運輸路線的信息(或概率分布)已知，但是實際上，由于對應急資源配置過程中存在較大的不確定性，獲取準確數據或概率分布非常困難。目前研究應急資源配置問題主要途徑之一是基于隨機優化[4-8]，但隨機優化存在一些局限：確定有代表性的情景及其概率比較困難；通常選取相對較少數量的情景，一定程度上限制了決策范圍；目標為最小化期望成本，未能體現決策者的風險偏好，如最壞情況下的策略等；大多為NP難問題，需用啟發式算法得到近似最優解。

近年來魯棒優化方法得到了迅速發展，在一定程度上彌補了隨機優化模型的局限，該方法早期由Ben-Tal等[9]提出，后經Bertsimas 和Sim[10]不斷發展，其關鍵是如何衡量不確定性，以特定不確定集合的形式表示未知參數的信息，其目標為最優系統最壞情況下的績效。此外，而且從某種程度上考慮了決策者的風險偏好。Ben-Tal 等[11]研究了不確定需求下的人道主義救援應急物流計劃問題，基于interval不確定需求集合，提出了可調節仿射變換的魯棒等價問題；Baron 和Naseraldin等[12]建立魯棒網絡設施選址模型，考慮多周期、多產品的不確定需求，確定新建設施的位置、數量、容量、產量等參數，且考慮box和ellipsoid需求不確定集合；張玲等[13]利用魯棒優化方法建立基于interval不確定需求集合的災后應急救災網絡規劃模型；陳濤等[14]在調研國內外相關研究的基礎上，以地震為背景提出了基于信息更新的資源調配決策問題，建立了兩階段魯棒-隨機優化模型；俞武揚[15]針對災害發生前受災地點的應急資源需求和交通網絡的不確定性，建立了不確定網絡結構下的兩階段應急資源魯棒配置模型。從目前的文獻來看，基于魯棒優化的應急資源的配置問題研究較少，大多僅考慮選址(Location)、選址-分配(Location-allocation)決策，基本采用離散情景分析或者簡單的interval或box不確定集合。

鑒于此，基于應急資源配置的災前預防準備和災后的響應分配問題，本文研究多類應急資源配置的魯棒選址-路徑優化分配問題，重點突出多類應急資源臨時供應點的選址布局和各類應急資源的路徑分配。考慮多類應急資源(水、食物、藥品和帳篷等)成本的不確定性，引入兩類不確定集合(box 和ellipsoid)來刻畫應急資源的不確定成本，建立兩個多類應急資源魯棒選址-路徑優化調度模型，確定應急資源最優的供應點布局、資源分配路徑。由于魯棒模型本身不易求解，借助魯棒優化的獨特優勢，將其轉化為易求解處理確定的魯棒等價模型，同時引入兩個不確定水平參數，調節解的最優性和魯棒性；最后通過我國四川北部和西部自然災害多發區的19個縣市進行四類應急資源的優化配置分析，驗證模型的可行性和有效性，為相關的應急救災部門提供建議。

2 多類應急資源魯棒選址-路徑優化模型

2.1問題描述

假設在自然災害發生前的預防準備階段存在多個潛在的受災點和應急資源供應的候選點，本文中受災點同時也是應急資源臨時供應的候選地點，考慮多類應急資源(食品、水、帳篷、藥品等)的配置，要在潛在的受災點中選出應急資源的臨時供應點，并對各類資源的最優供應量和路徑做出預決策，以滿足災區需求。基本的符號說明如下：D為所有的節點的集合，假設每一個節點既是受災點j又是潛在的臨時供應點i，i,j∈D；L為路線的集合，(i,j)∈L；M為應急資源種類的集合，m∈M；k為建立臨時供應點的最大數量；fi為臨時供應點i處的建立成本；tijm為在路線(i,j)上單位應急資源m的運輸成本；djm為受災點j處對應急資源m的需求量；vim為應急資源m在臨時供應點i處的最大容量；Φ為一個充分大的數；cim為臨時供應點i處應急資源m的單位成本。決策變量：xi=1，如果在受災點i處建立臨時供應點，否則xi=0；zijm為在路線(i,j)上應急資源m的調度數量；yijm為臨時供應點i滿足受災點j應急資源m的比例。因此，應急資源配置的選址-路徑優化名義(Nominal)模型為：

(1)

(2)

(3)

yijm≤xi?i,j∈D,m∈M

(4)

(5)

(6)

(7)

(8)

xi∈{0,1},yijm,zijm≥0 ?i,j∈D,m∈M

(9)

在名義模型中，目標函數式(1)為總成本最小化，包括建立臨時供應點的成本、運輸成本和資源成本；約束式(2)表示每個受災點的需求都要滿足；約束式(3)表示建立臨時供應點數量限制；約束式(4)表示只有建立臨時供應點才能夠提供需求；約束式(5)表示臨時供應點的應急資源分配量，即流入量與流出量之差，至少滿足受災點的需求；約束式(6)表示臨時供應點的流入、流出和需求應該不大于容量限制；約束式(7)和(8)表示受災點的流入、流出等于需求；約束式(9)為0-1變量和非負變量。

2.2不確定成本下應急資源魯棒選址-路徑模型

自然災害發生前后，由于應急資源緊缺，資源成本波動較大，應急資源的成本具有明顯的不確定性，因此，本文在名義模型的基礎上，考慮應急資源的成本不確定性，分別引入box和ellipsoid不確定集刻畫多類資源的不確定成本c，運用魯棒優化方法，建立多類應急資源配置的魯棒選址-路徑優化模型。

(1)基于box不確定集合的應急資源魯棒選址-路徑模型

(10)

s.t.(2), (3), (4), (5), (6), (7), (8), (9)

當Γ=0時，box不確定集魯棒模型等價于名義模型。此目標函數中存在內層最大化問題，接下來將其轉換為更易于求解的魯棒等價模型。

考慮內層最大化的線性規劃問題:

0≤uim≤1,?i∈D,m∈M

(11)

根據強對偶原理，該問題等價為(12)，其中ρim,θ為對偶變量。

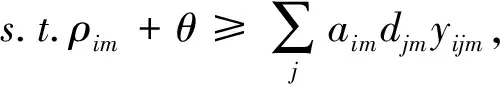
ρim,θ≥0,?i∈D,m∈M

(12)

綜上，將(11)和(12)，代入問題(10)，將非線性的魯棒模型轉化為確定的線性魯棒等價模型(13)，且該模型為混合線性整數規劃問題，因此較易求解。

yijm≤xi?i,j∈D,m∈M

xi∈{0,1},yijm,zijm,ρim,θ≥0 ?i,j∈D,m∈M

(13)

(2)基于ellipsoid不確定集的應急資源魯棒選址-路徑模型

mint

(14)

(15)

(16)

令:

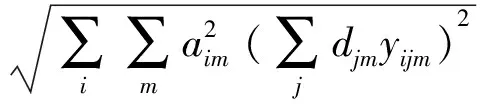
(17)

則:

(18)

因此，借助魯棒優化，建立應急資源配置的魯棒選址-路徑優化模型，并轉化為易求解處理確定的魯棒等價模型。由于魯棒等價模型為混合線性整數規劃(13)或二階錐規劃(19)，當求解問題的規模不是很大時，尤其對于二次規劃問題時，可使用現有的數學軟件求解。本文所有代碼用GAMS編程，并調用CPLEX中的分支-切割算法和內點算法求解。

mint

djmyijm+ΩW≤t

yijm≤xi?i,j∈D,m∈M

xi∈{0,1},yijm,zijm≥0 ?i,j∈D,m∈M

(19)

3 算例分析

四川北部和西部地區是地震、泥石流、滑坡等自然災害發生比較密集的區域[16]，選取龍門山斷裂帶及其鄰區作為地震等自然災害發生的潛在區域。模型中的潛在的受災點同時也是應急資源臨時供應的候選地點，選取可能的受災點有理縣、汶川、茂縣、都江堰、崇州、郫縣、彭州、什邡、綿竹、安縣、北川、江油、廣漢、中江、三臺、鹽亭、射洪、大英和梓潼共19個縣市，依次標號1, 2, …, 19，從其中選出5個應急資源臨時供應點，滿足各受災點的需求。根據2014年四川省統計年鑒、物價水平以及各地區的人均GDP，考慮飲用水、食品、藥品和帳篷四種應急資源，且1升水的體積為0.01立方米，1千克食品的體積為0.1立方米，1盒藥品的體積為0.05立方米，1頂帳篷的體積為0.2立方米，各潛在的受災點的各類資源的需求和臨時供應點的倉庫容量及建設成本如表1所示，其中各受災點的需求是根據各地區人口密度估計；表2為各受災點應急資源的單位成本，根據各受災點的人均生產總值估計；路線(i,j)單位運輸成本根據google地圖的路線距離和單位資源的體積得到；本文考慮各類應急資源單位成本的不確定性，則成本的擾動比例ε為10%。

接下來選取Γ=Ω=7，擾動比例ε為10%，并且選取應急資源中的飲用水資源為例，對兩個魯棒選址-路徑優化模型進行求解。通過算法求解，名義模型、box和ellipsoid不確定集合下的魯棒模型的最優的選址點和運輸路徑分別見圖1、圖2、圖3，其中橢圓表示選擇的最優的臨時資源供應點，箭頭表示最優的分配路徑，具體路線按照google地圖上自動獲得。在確定的名義模型和box不確定集模型中，均選取汶川、崇州、廣漢、北川和三臺共五個縣市作為應急資源的臨時供應點，但資源分配路徑不同，例如確定模型中都江堰的飲用水來自于汶川，即汶川→都江堰，而在box不確定集合模型中，都江堰的飲用水來自于崇州，中間經郫縣，即崇州→郫縣→都江堰，即崇州作為飲用水的臨時供應點，為崇州、郫縣、都江堰供應飲用水，載滿飲用水的車輛從崇州出發(先滿足自身需求)，在前往都江堰的途中經過郫縣，滿足郫縣的飲用水資源的需求(它的下一個節點是都江堰，并沒有其它的分支)，然后繼續沿著這個路線前往都江堰。表3為box不確定集下的魯棒選址-路徑模型的飲用水的調度分配量，正如圖2所顯示的應急資源的運輸路徑一樣，其中北川為6個災區縣市提供飲用水資源；而ellipsoid不確定集模型的最優資源臨時供應點則有所不同，具體是汶川、崇州、什邡、北川和三臺，沒有選取廣漢，而新增加什邡，如表3和4中加粗顯示的部分，因此飲用水的調度分配路徑發生變化，如圖3所示，表4為ellipsoid不確定集下的魯棒選址-路徑模型的飲用水的調度分配量，與表3相比，在其他所有條件不變的情況下，供應點北川供應的6個受災點相同，但是飲用水資源的供應量發生變化，如表3和表4中加粗部分。類似，新增加的供應點什邡供應受災點的需求也發生變化。

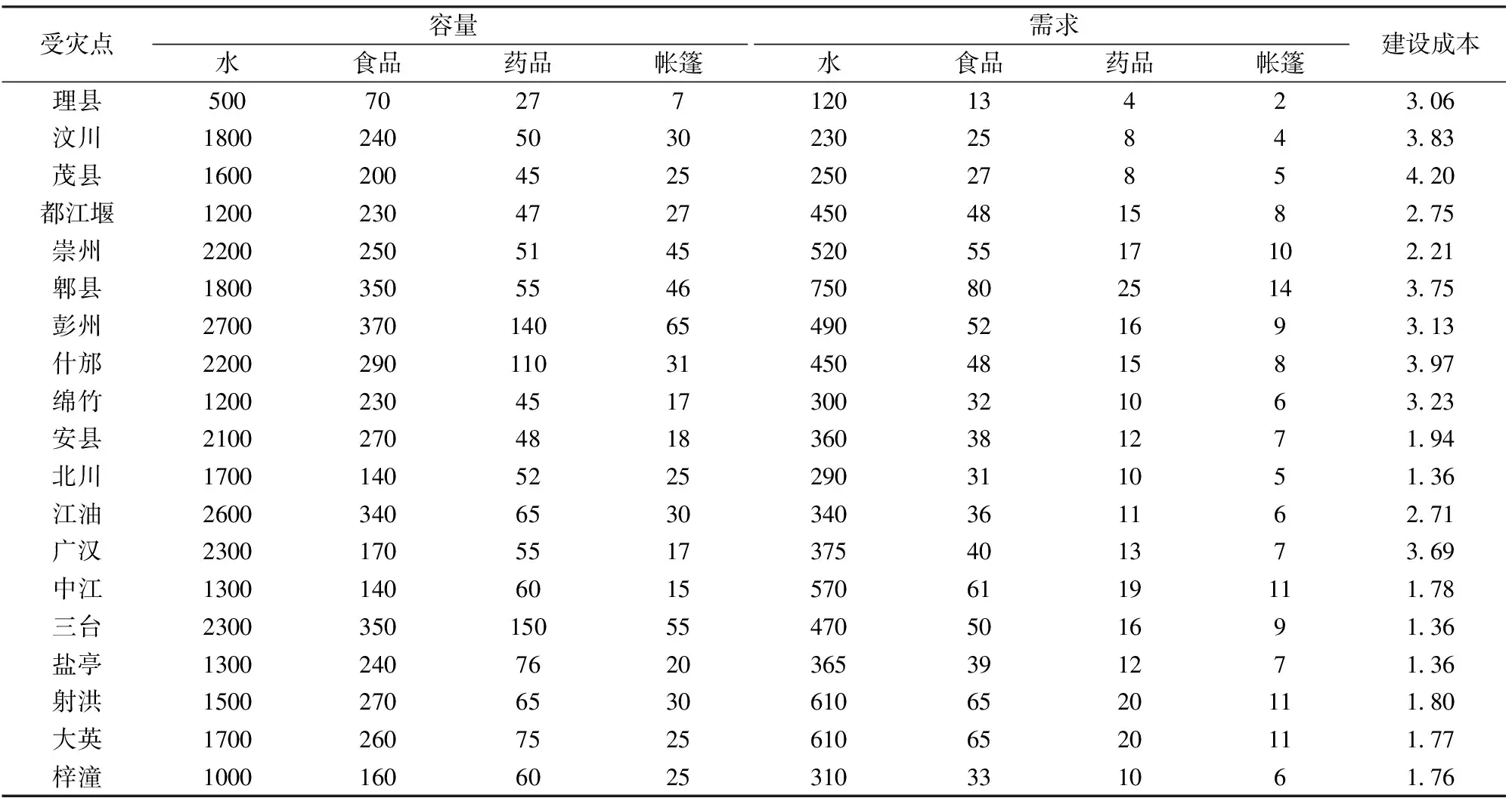
表1 潛在受災點應急資源的容量限制、需求(萬)及建設成本(萬元)

表2 受災點應急資源的成本(元/單位)

圖1 名義( nominal)模型的最優選址布局和分配路徑，資源：水

圖2 box不確定集合模型的最優選址布局和分配路徑，資源：水

圖3 ellipsoid不確定集合模型的最優選址布局和分配路徑，資源：水

當Γ=Ω=0時，box和ellipsoid不確定集合下的魯棒模型與確定的名義模型等價，此時最小成本為5.68億，圖4為三個模型的總成本隨不確定水平參數Γ,Ω變化的曲線，隨著不確定水平參數的增加，總成本逐漸增加，其中Γ=Ω時，ellipsoid不確定集模型增加迅速，對于box不確定集模型，總成本不斷增加，但是增加的幅度逐漸減少，當Γ≥19時保持不變，因為選取19個候選地點，則0≤Γ≤19，當Γ=19時，該問題等價于絕對魯棒模型，此時總成本最大為6.25億。但是ellipsoid不確定集模型的成本明顯高于box不確定集模型，這是因為Γ=Ω時，ellipsoid不確定集的幾何空間大于box不確定集，因此結果表明，對于相同參數設置的環境下，ellipsoid不確定集合模型比box不確定集合模型保守，成本較高。由于在魯棒優化模型中不確定水平參數在一定程度上度量決策者的保守性和風險厭惡程度，因此決策者可根據自己的風險厭惡程度選擇適當Γ和Ω，進而確定應急資源的分配方案。

表3 box不確定集下應急資源(水)的最優調度數量Γ=7,εi=0.1

表4 ellipsoid不確定集下應急資源(水)的最優調度數量Ω=7,εi=0.1

此外，改變擾動比例εi，選取5%、10%、15%，Γ/Ω分別取0, 1, 3, 5, 7, 9，此時在不同的不確定水平參數，不同的擾動比例組合下的最小總成本和最優的應急資源的臨時供應選址點如表5所示。隨著不確定水平參數和擾動比例的增加，最優的選址點發生變化，發生變化的部分加粗顯示，最小總成本增加，但ellipsoid不確定集模型的成本相對較高，這與前面提到的ellipsoid不確定集合下的魯棒模型較保守的結論一致。

表5 box 和ellipsoid不確定集及成本擾動比例組合下的總成本和選址點

圖4 nominal, box, ellipsoid模型的總成本隨不確定水平參數的變化

4 結語

本文基于應急資源配置的災前預防準備和災后的響應分配問題，考慮多類應急資源(飲用水、食品、藥品、帳篷)成本的不確定性，引入兩類不確定集合(box 和ellipsoid)來刻畫應急資源成本的不確定性，并提出兩個多類應急資源魯棒選址-路徑優化模型，這在一定程度上降低不確定性帶來的風險。最后，通過我國四川北部和西部自然災害多發區的19個縣市的相關數據進行分析，確定最優的應急資源臨時供應點選址布局、應急資源的運輸分配路徑方案，同時考慮資源成本擾動比例的靈敏度分析，驗證模型的可行性和有效性。通過確定模型與兩類不確定集合的魯棒模型的比較，發現在其他條件相同的情況下，ellipsoid不確定集合下的魯棒模型較保守，資源配置的總成本較高。由于在魯棒優化模型中的不確定水平參數在一定程度上度量決策者的保守性和風險厭惡程度，因此決策者可以根據自己的風險厭惡程度選擇適當不確定水平參數的值，確定應急資源的配置方案，進而為相關應急救災部門在災前預防準備工作提供參考和決策支持。然而本文僅考慮應急資源成本不確定性，而在應急資源配置過程中存在供給、需求及路徑中斷等不確定性，可以研究更多不確定因素，同時考慮動態多階段的應急資源配置問題，這是接下來的研究方向。

[1] 中華人民共和國國務院新聞辦公室. 《中國的減災行動》白皮書[EB/OL].[2009-05-11].news.xinhua net.com/newscen-ter/2009-05111/cont-ent_12351082.htm.

[2] Altay N, Green W G. OR/MS research in disaster operations management[J]. European Journal of Operational Research, 2006, 175(1): 475-493.

[3] Galindo G, Batta R. Review of recent developments in OR/MS research in disaster operations management[J]. European Journal of Operational Research, 2013, 230(2): 201-211.

[4] Mete H O, Zabinsky Z B. Stochastic optimization of medical supply location and distribution in disaster management[J]. International Journal of Production Economics, 2010, 126(1): 76-84.

[5] 葛洪磊, 劉南. 復雜災害情景下應急資源配置的隨機規劃模型[J]. 系統工程理論與實踐, 2014, 34(12): 3034-3042.

[7] Jia Hongzhong, Ordóez F, Dessouky M. A modeling framework for facility location of medical services for large-scale emergencies[J]. IIE Transactions, 2007, 39(1): 41-55.

[8] Verma A, Gaukler G M. Pre-positioning disaster response facilities at safe locations: An evaluation of deterministic and stochastic modeling approaches[J]. Computers & Operations Research, 2015, 62: 197-209.

[9] Ben-Tal A, El Ghaoui L, Nemirovski A. Robust optimization [M]. Princeton:Princeton University Press, 2009.

[10] Bertsimas D, Sim M. The price of robustness[J]. Operations Research, 2004, 52(1): 35-53.

[11] Ben-Tal A, Do Chung B, Mandala S R, et al. Robust optimization for emergency logistics planning: Risk mitigation in humanitarian relief supply chains[J]. Transportation Research Part B: Methodological, 2011, 45(8): 1177-1189.

[12] Baron O, Milner J, Naseraldin H. Facility location: A robust optimization approach[J]. Production and Operations Management, 2011, 20(5): 772-785.

[13] 張玲, 王晶, 張敏. 基于不確定需求的災后應急救災網絡規劃模型與算法[J]. 運籌與管理, 2014, 23(3): 49-55.

[14] 陳濤, 黃鈞, 朱建明. 基于信息更新的兩階段魯棒-隨機優化調配模型研究[J]. 中國管理科學, 2015, 23(10): 66-77.

[15] 俞武揚. 不確定網絡結構下的應急物資魯棒配置模型[J]. 控制與決策, 2013, 28(12): 1898-1902.

[16] 楊濤, 鄧榮貴. 四川地區地震崩塌滑坡的基本特征及危險性分區[J]. 山地學報, 2002, 20(4): 456-460.

Multiple Relief Resources Robust Location-Routing Optimization

PENGChun,LIJin-lin,WANGShan-shan,RANLun

(School of Management and Economics, Beijing Institute of Technology, Beijing 100081, China)

Decisions to support preparedness activities for disastermanagement are challenging due to the uncertainties of parameters,the balance preparedness and risk, so it is a hot topic. In this paper multiple relief resources location-routing problem is addressed to determine optimal deployment of supply facilities for multiple relief resources, transport distribution route. However, traditional methods addressing this problem mainly focus on stochastic optimization by assuming probability distribution to measure the uncertainty, there are some drawbacks. Multiple relief resources cost uncertainty is considered, introducing two types of uncertainty sets, i.e. box and ellipsoid, to capture the uncertain cost of multiple relief resources, and multiple relief resources robust location-routing models are proposed respectively, which are converted into the deterministic robust equivalent models, and can be solved by hybrid programming algorithm coded in GAMS and CPLEX. Finally, the 19 cities in the north and west of Sichuan Province are chosen to conduct the numerical study. Results show that the proposed robust models is feasible and effective, and compared to the robust model based on box uncertainty set, under the same parameter setting, robust model based on ellipsoid uncertainty set usually is more conservative, and leads to a higher total cost. Decision-makers, according to their risk aversion and conservativeness, choose an appropriate value for the uncertain level parameters Γ/Ω to get the optimal solution, and provide decision support to the department of Emergency Disaster Relief.

relief resource; location-routing; cost uncertainty; robust optimization; uncertainty set

1003-207(2017)06-0113-08

10.16381/j.cnki.issn1003-207x.2017.06.015

2016-05-04；

：2016-07-29

國家自然科學基金資助重點項目(71432002)；國家自然科學基金面上資助項目(71172172);北京理工大學研究生國際學術交流項目(1320012351601)

李金林(1955—)，男(漢族)，北京理工大學管理與經濟學院，教授，博士生導師，研究方向：醫療與健康數據分析與決策、收益管理，E-mail:jinlinli@bit.edu.cn.

O224;F224.3

：A