三維超聲速流動的壓力反問題

藍(lán)慶生, 趙玉新,*, 趙一龍, 劉紅陽

(1.國防科技大學(xué) 高超聲速沖壓發(fā)動機(jī)技術(shù)重點(diǎn)實(shí)驗(yàn)室, 湖南 長沙 410073;2.中國空氣動力研究與發(fā)展中心 計(jì)算空氣動力研究所, 四川 綿陽 621000)

?

三維超聲速流動的壓力反問題

藍(lán)慶生1, 趙玉新1,*, 趙一龍1, 劉紅陽2

(1.國防科技大學(xué) 高超聲速沖壓發(fā)動機(jī)技術(shù)重點(diǎn)實(shí)驗(yàn)室, 湖南 長沙 410073;2.中國空氣動力研究與發(fā)展中心 計(jì)算空氣動力研究所, 四川 綿陽 621000)

為了進(jìn)一步探索三維超聲速流道的設(shè)計(jì)方法，采用一種預(yù)設(shè)壁面壓力分布計(jì)算壁面型線的思想，并結(jié)合雙特征線方法提出一種全三維超聲速流動壓力反問題的求解方法。在三維超聲速流場設(shè)計(jì)中，可直接根據(jù)來流條件和壁面壓力分布求解壁面的三維坐標(biāo)，通過空間步進(jìn)的方式，使得解在一系列解平面上推進(jìn)，從而使得所設(shè)計(jì)的型面與預(yù)設(shè)的壁面壓力分布相容。通過Prandtl-Meyer膨脹波的理論解驗(yàn)證了該格式的設(shè)計(jì)精度。根據(jù)預(yù)設(shè)的壓力分布，設(shè)計(jì)了圓形和橢圓形入口的三維超聲速噴管，并將設(shè)計(jì)方法與數(shù)值模擬進(jìn)行對比驗(yàn)證。驗(yàn)證結(jié)果表明：所設(shè)計(jì)的流場與CFD計(jì)算得到的等值線符合得較好，因此基于雙特征線的壓力反問題求解方法具備三維超聲速氣動設(shè)計(jì)的能力，并具有純?nèi)S、高精度、壁面壓力分布可控的優(yōu)勢，對未來高超聲速氣動設(shè)計(jì)應(yīng)用將起到重要的支撐作用。

壓力反問題；雙特征線方法；三維超聲速氣動設(shè)計(jì)；壁面壓力分布可控

0 引 言

特征線法是一種數(shù)值求解無粘流動的重要方法。關(guān)于二維特征線的方法和應(yīng)用，國內(nèi)外都有了很多相關(guān)成果[1-4]，相比之下三維特征線的應(yīng)用較少[5]。而現(xiàn)階段隨著機(jī)體/發(fā)動機(jī)一體化設(shè)計(jì)概念的提出，對超聲速流道高效轉(zhuǎn)彎變形的需求也日漸增長，圓形和橢圓形等流道設(shè)計(jì)再次成為國際上的研究熱點(diǎn)[6-7]，這類流道通常需要實(shí)現(xiàn)三維空間復(fù)雜曲面的均勻過渡，因此流動的三維特性進(jìn)一步增加了對高精度、純?nèi)S數(shù)值方法的需求。

在三維氣動設(shè)計(jì)的研究過程中出現(xiàn)過許多精妙的構(gòu)思，如Busemann進(jìn)氣道，流線追蹤技術(shù)及密切理論、三維乘波體設(shè)計(jì)等。但是流線追蹤方法主要限制于基準(zhǔn)流場的設(shè)計(jì)[8-10]；在一定強(qiáng)幾何約束條件下，密切理論難以直接應(yīng)用于三維流場的精確組織[11-12]；流線幾何融合能夠?qū)崿F(xiàn)變截面壓縮，但其融合主要是從幾何的角度出發(fā)，并未考慮到流場的特征，使得壓縮不好控制而出現(xiàn)流向渦[13]。因此尋找一種新的三維超聲速流場的設(shè)計(jì)方法至關(guān)重要。

2013年南京航空航天大學(xué)的全志斌等人設(shè)計(jì)了壁面壓力分布可控的單邊膨脹噴管[14]。2015年，國防科學(xué)技術(shù)大學(xué)的趙玉新等人提出一種三維超聲速流動的壓力反問題，并構(gòu)造了邊界反Riemann求解器[15]，實(shí)現(xiàn)了入口為矩形、橢圓形、扇環(huán)形流管的三維反設(shè)計(jì)。2016年廈門大學(xué)的李怡慶等人設(shè)計(jì)了壁面壓力分布可控的高超聲速進(jìn)氣道[16]。此外文獻(xiàn)[17]中提出了全三維超聲速流場的求解方法，以及基于特征線追蹤的氣動反設(shè)計(jì)方法，現(xiàn)已成功運(yùn)用于圓轉(zhuǎn)方超聲速流道的設(shè)計(jì)中[18-19]。

為了進(jìn)一步探索純?nèi)S超聲速流場壓力反問題的求解方法，本文通過分析三維特征線方法[20-21]，采用預(yù)設(shè)壁面壓力分布計(jì)算壁面型線的思想，提出了基于雙特征線的壓力反問題求解方法。為了驗(yàn)證設(shè)計(jì)方法的可靠性，本文對設(shè)計(jì)的噴管構(gòu)型進(jìn)行CFD數(shù)值模擬，并將其與設(shè)計(jì)流場進(jìn)行分析比較。結(jié)果表明：基于雙特征線方法的壓力反問題求解器具備三維超聲速與高超聲速氣動設(shè)計(jì)的能力，同時(shí)具有高精度、純?nèi)S、易控制的特性，對未來高超聲速氣動設(shè)計(jì)應(yīng)用將起到重要的支撐作用。

1 雙特征線算法

1.1 特征方程及相容方程

三維定常、無粘、可壓、等熵流動的控制方程為：

(1)

(2)

(3)

(4)

(5)

(6)

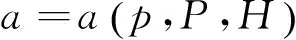
(7)

其中，u、v、w為x、y、z方向的速度，p為靜壓，ρ為密度，a為聲速，P為總壓，H為總焓，下標(biāo)x、y、z表示對x、y、z坐標(biāo)方向的方向?qū)?shù)。這些方程可以寫成如下所示的定常三維等熵超聲速流動的特征方程和相容性方程[2]。

特征方程：

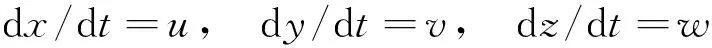
(8)

[u2-(V2-a2)](dx)2+[v2-(V2-a2)](dy)2+[w2-(V2-a2)](dz)2+2uvdxdy

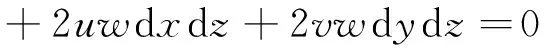
(9)

相容方程：

(10)

(11)

ρa(bǔ)nxut+ρa(bǔ)nyvt+ρa(bǔ)nzwt-pt

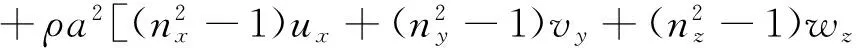
(12)

其中：n=inx+jny+knz，為特征法線，a為當(dāng)?shù)芈曀伲聵?biāo)t表示在特征方向的方向?qū)?shù)。

1.2 雙特征線方法單元過程

在進(jìn)行數(shù)值求解時(shí)，特征方程決定離散網(wǎng)格點(diǎn)，相容方程決定解點(diǎn)流動參數(shù)。本文采用的是Butler提出的五面體雙特征線網(wǎng)格[20-21]，如圖1所示。該格式采用空間步進(jìn)的方法，使得解在一系列平行的解平面上推進(jìn)。

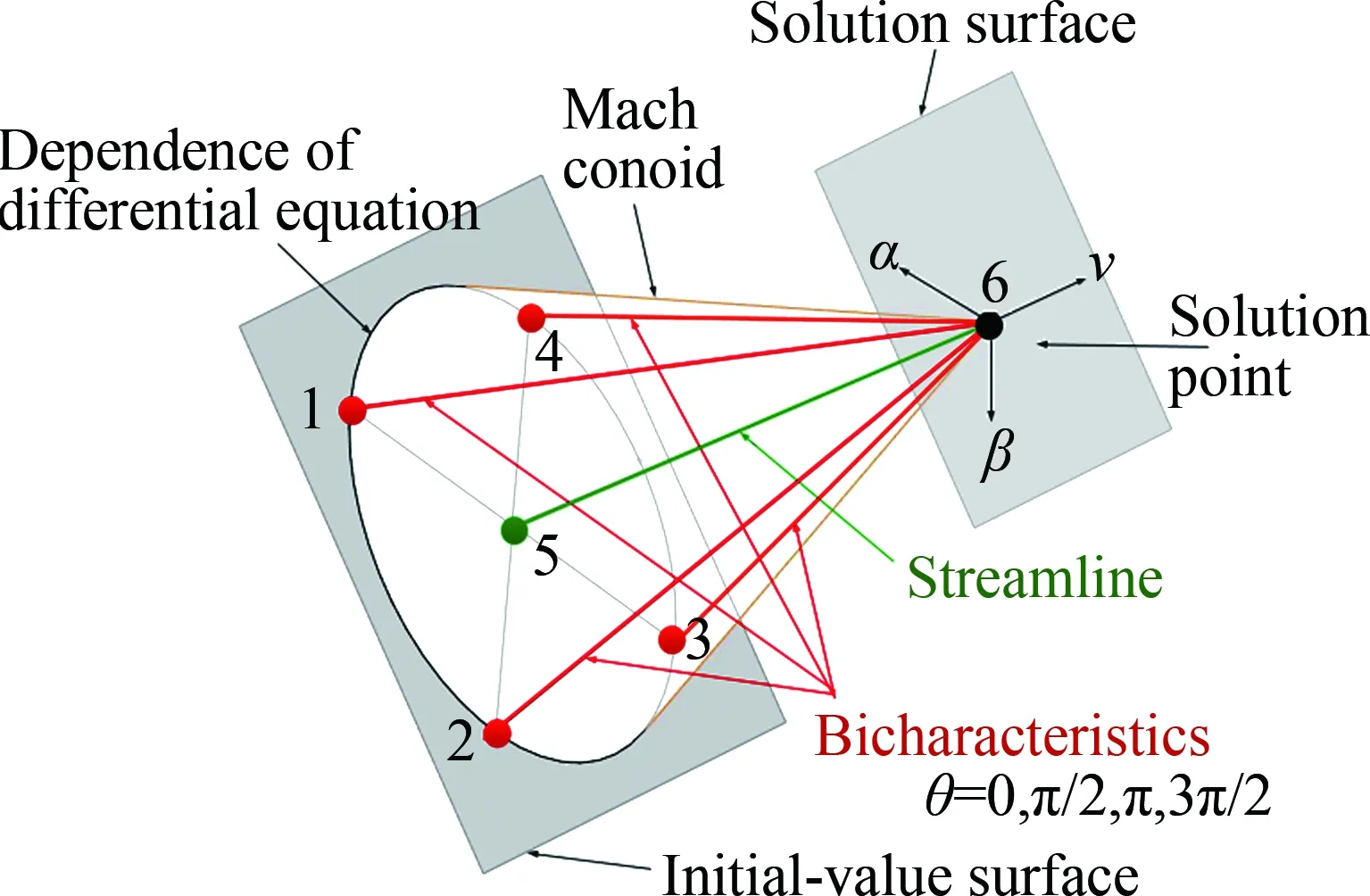
圖1 五面體雙特征曲線網(wǎng)格Fig.1 Pentahedral line network

圖中點(diǎn)5為微團(tuán)軌跡與初值面的交點(diǎn)，點(diǎn)6為解點(diǎn)，其位置由點(diǎn)5向前延伸微團(tuán)軌跡來確定。隨后四條間隔相同的雙特征線從點(diǎn)6向后延伸，與初值面在點(diǎn)1、2、3和點(diǎn)4處相交。點(diǎn)1～點(diǎn)5上的流動參數(shù)由擬合了點(diǎn)5和八個(gè)相鄰點(diǎn)的雙變量內(nèi)插多項(xiàng)式來確定。

此外，Butler還引進(jìn)了雙特征線的參數(shù)化，如下式所示。

(14)

其中a表示當(dāng)?shù)芈曀佟?/p>

Butler還從原先偏微分方程的線性組合導(dǎo)出一個(gè)在微團(tuán)軌跡上能夠成立的非特征線關(guān)系式：

(15)

其中dup定義為壓力沿流線切向的導(dǎo)數(shù)。

四個(gè)雙特征線相容性方程可以用θ=0，π/2，π，3π/2寫出，再將這四個(gè)方程與式(15)進(jìn)行有限差分。這五個(gè)有限差分方程可進(jìn)行線性組合，從而獲得三個(gè)相互獨(dú)立的方程，同時(shí)也能消除解點(diǎn)上的交叉倒數(shù)。這三個(gè)獨(dú)立的方程加上在微團(tuán)軌跡上成立的兩個(gè)相容性方程，用改進(jìn)的歐拉預(yù)估-校正法進(jìn)行求解。為達(dá)到二階精度，在校正步時(shí)對相容性方程系數(shù)取平均。

對于無粘情況下的固體邊界，流體必須與邊界相切。用流線相切的條件代替四條雙特征線之一的相容性方程，內(nèi)點(diǎn)單元即可修改為邊界單元。流動相切條件為：

(16)

其中ni是點(diǎn)6固體邊界的單位外法線。

(17)

其中Rmin是流線與初值面的交點(diǎn)和用來構(gòu)成有限差分網(wǎng)格凸包的點(diǎn)中離得最近的那個(gè)點(diǎn)之間的距離。

2 壓力反問題求解器

2.1 特征線求解技術(shù)

如圖2所示，在點(diǎn)5建立基準(zhǔn)面，該基準(zhǔn)面由向量OP1和向量OP2共同構(gòu)成，其中OP1與點(diǎn)5左右兩點(diǎn)的連線相互平行，OP2為向量(1,0,0)。直線L56為流線微元。密切面由矢量V和上游的βi共同構(gòu)成，V為點(diǎn)5和點(diǎn)6的平均速度矢量，βi為流動相切條件中的ni。流線L56為由密切面和旋轉(zhuǎn)θ角的基準(zhǔn)面相貫獲得，旋轉(zhuǎn)角度的正方向滿足旋轉(zhuǎn)軸為OP1的右手定則。因此存在一個(gè)單調(diào)關(guān)系：

(18)

因此，P6i會隨著θi的增大而減小，反之亦然。通過給定點(diǎn)6壓力的設(shè)計(jì)值，反求對應(yīng)的θ值，從而獲得點(diǎn)6坐標(biāo)，這就是壓力反問題。

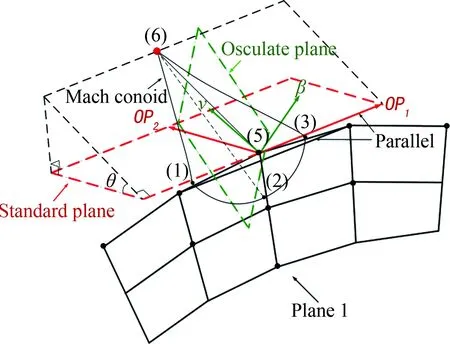
圖2 壓力反問題單元過程Fig.2 Unit process of pressure inverse problem

2.2 方法精度驗(yàn)證

本小節(jié)對該求解器的精度進(jìn)行驗(yàn)證。設(shè)計(jì)的算例模型如圖3所示，外折角為20°，來流馬赫數(shù)為1.4，總壓為101 325 Pa，總溫為288 K，氣體常數(shù)為287 J/(kg·K)，比熱比為1.4。假設(shè)圖中矩形區(qū)域內(nèi)未受到上壁面反射膨脹波的影響，故其精確流場可用普朗特-邁耶函數(shù)求得。圖4中黑色等值線為馬赫線的精確解，從頂點(diǎn)處(0.2449，0.25)追蹤一條流線，將其上的壓力分布作為反問題求解器的輸入項(xiàng)。

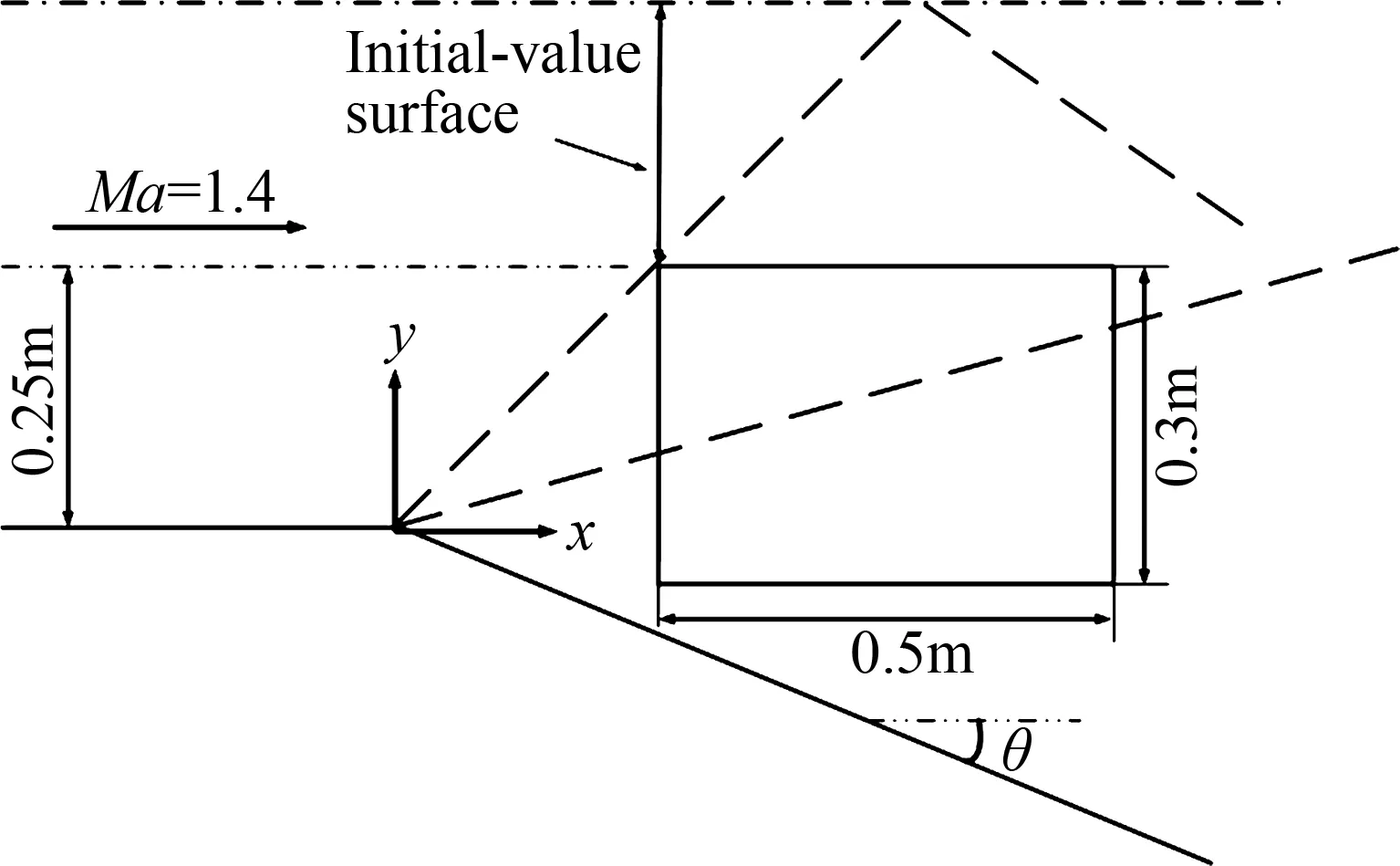
圖3 精度驗(yàn)證算例模型Fig.3 A case for accuracy validation

初始截面所在位置已在圖3中標(biāo)示，設(shè)z方向垂直于紙面向外，則初始截面在yz平面內(nèi)，分別沿y、z方向設(shè)定40、20個(gè)計(jì)算節(jié)點(diǎn)。x為流動方向，沿流向步進(jìn)80步，獲得如圖4所示的馬赫數(shù)等值線，其中紅色等值線為求解器求得，黑色等值線為精確解。從圖4中可以看出，該方法所求得的馬赫線和理論幾乎完全重合。壁面上各流動參數(shù)與精確解的最大相對誤差見表1。從表1中可以看出，求解器繼承了特征線高精度的特性。

圖4 特征線解與精確解對比Fig.4 Comparison between analytical and bicharacteristics solutions for PM flow表1 設(shè)計(jì)方法與Prandtl-Meyer精確解對比的最大相對誤差Table 1 Maximal relative error of the design method comparing with Prandtl-Meyer flow

p/Paρ/(kg·m-3)u/(m·s-1)v/(m·s-1)MaP0/Pa87.441.38.60.29

3 三維超聲速噴管設(shè)計(jì)算例

為了驗(yàn)證壓力反問題求解方法的有效性，針對進(jìn)口為圓形、橢圓形的噴管進(jìn)行設(shè)計(jì)，入口條件為馬赫數(shù)為1.05的平行均勻流，總壓為101 325 Pa，總溫為288 K，比熱比為1.4，氣體常數(shù)為287 J/(kg·K)。在壁面上調(diào)用壓力反問題求解器，內(nèi)部流場采用雙特征線方法進(jìn)行計(jì)算。

若預(yù)設(shè)的壁面壓力變化過于劇烈，容易出現(xiàn)強(qiáng)壓縮或者膨脹波，因此本文計(jì)算了一個(gè)超橢圓噴管，將其壁面壓力分布作為一個(gè)較為合理的壁面壓力分布，如圖5所示。其中超橢圓的壁面函數(shù)為：

(19)

其中：z0=y0=0.1+0.4x2。

圖5 預(yù)設(shè)的壁面壓力分布Fig.5 Preassigned pressure distribution

3.1 圓形入口的噴管設(shè)計(jì)

噴管的進(jìn)口截面設(shè)為R=0.1 m的圓，考慮空間的對稱性，為了減少計(jì)算量，僅計(jì)算1/4圓。初始截面的結(jié)構(gòu)網(wǎng)格采用放射狀的方式劃分。x方向?yàn)榱鲃臃较颍瑖姽苎?x向的視圖如圖6所示。沿流動方向空間步進(jìn)400次，步進(jìn)距離為0.347 m，網(wǎng)格量為21×21×400，在主頻為2.6 GHZ的PC上運(yùn)行時(shí)間需要120 s。圖6中可以看出，每一條沿j向的網(wǎng)格線均表示一個(gè)流面切片，每一個(gè)流面均通過軸線，說明氣體在噴管內(nèi)部嚴(yán)格地沿著徑向流動，符合軸對稱規(guī)律。

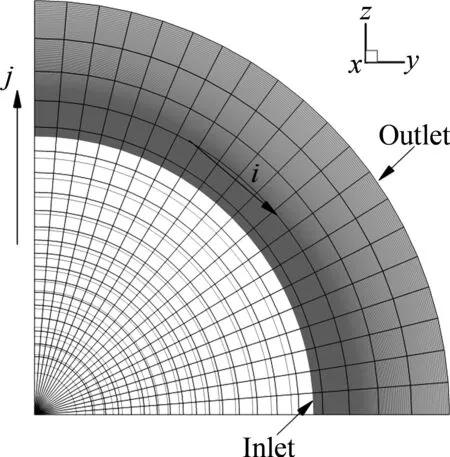
圖6 圓形進(jìn)口噴管沿-x方向的視圖Fig.6 View of nozzle with circle inlet along -x direction

圖7為給定壓力的原始噴管型線與設(shè)計(jì)型線的對比，其中綠色點(diǎn)表示原始噴管軸對稱面上的壁面型線，紅色線條為設(shè)計(jì)噴管的壁面型線。圖8為對比了軸線和壁面的馬赫數(shù)分布，同樣綠色的點(diǎn)表示給定的流場數(shù)據(jù)，紅色線條表示相應(yīng)的設(shè)計(jì)值。通過計(jì)算，中心馬赫數(shù)和壁面馬赫數(shù)的最大相對誤差分別為0.07%和0.1%。因此，該方法高精度地還原了給定壓力的原始構(gòu)型和原始流場。

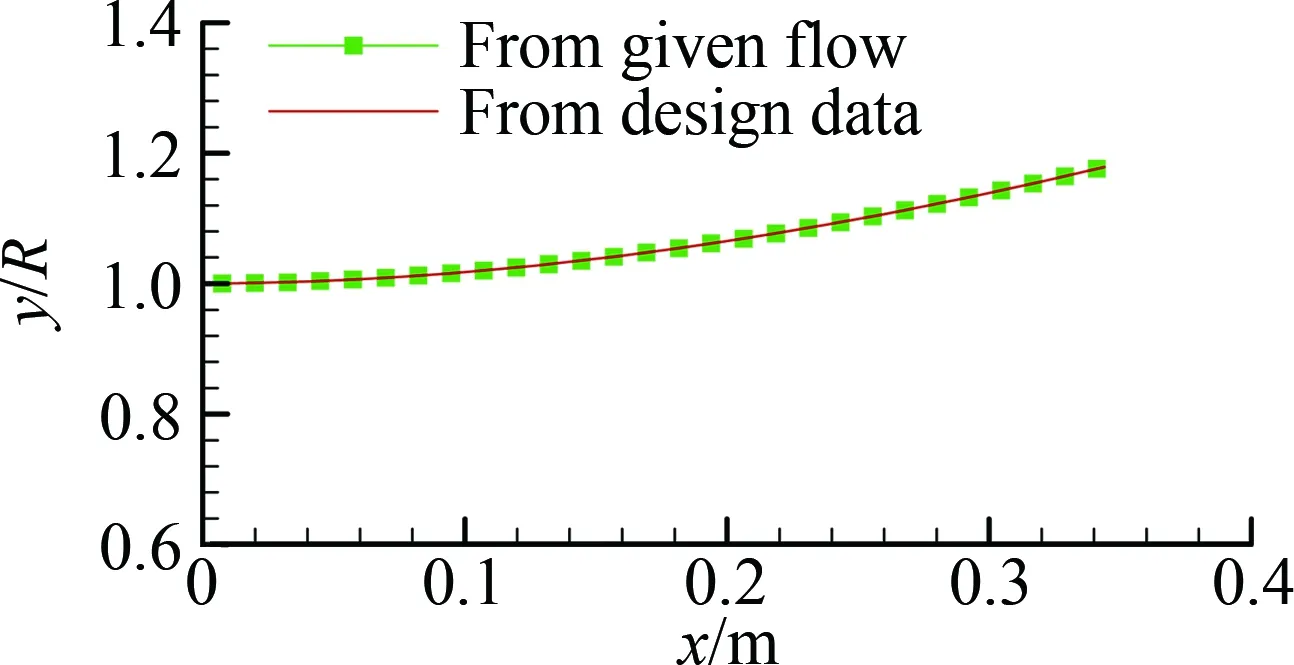
圖7 設(shè)計(jì)噴管型線與原始噴管對比Fig.7 Comparison between designed and original nozzle shape

圖8 設(shè)計(jì)馬赫數(shù)與原始馬赫數(shù)沿流向的對比Fig.8 Comparison between designed and original Mach number

為了進(jìn)一步證明該方法對原始流場的還原程度，本文比較了出口截面沿45°的參數(shù)分布，如圖9～圖11所示，對比了馬赫數(shù)、壓力、以及x軸的速度分量隨y的變化曲線。圖中可以看出，點(diǎn)和曲線幾乎完全重合，其最大相對誤差如表2所示，進(jìn)一步證明了設(shè)計(jì)程序的可靠性。

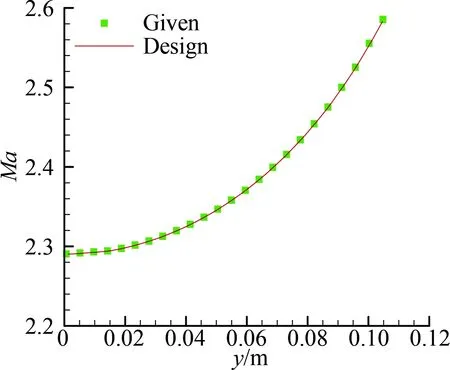
圖9 出口截面沿45°線的 馬赫數(shù)分布對比Fig.9 Comparison for Mach number along 45° direction in outlet section

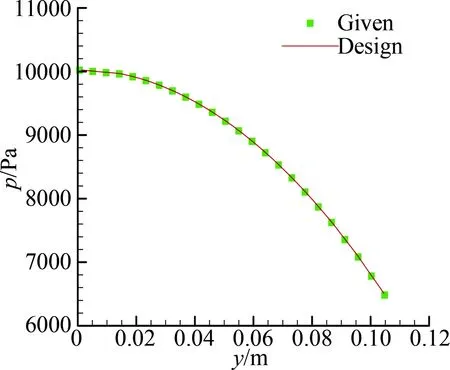
圖10 出口截面沿45°線的 壓力分布對比Fig.10 Comparison for pressure along 45° direction in outlet section

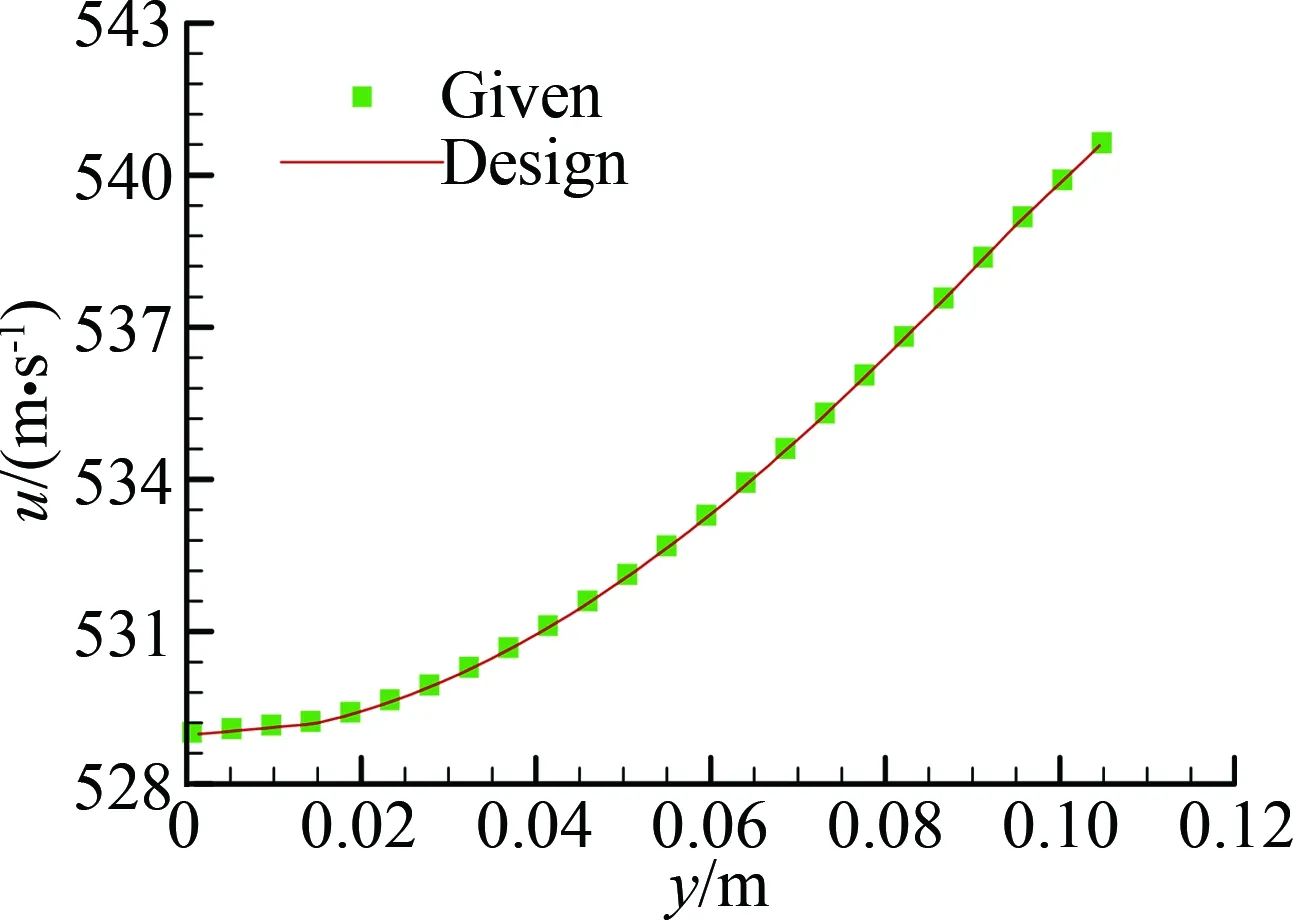
圖11 出口截面沿45°線的x方向 速度分布對比Fig.11 Comparison for x-component of velocity along 45° direction in outlet section

3.2 橢圓形入口的噴管設(shè)計(jì)

噴管的入口截面為橢圓形，長軸長0.15 m，短軸長0.1 m，流動參數(shù)與軸對稱噴管一致，同樣是馬赫數(shù)為1.05的平行均勻流。初始截面采用放射狀網(wǎng)格，x方向表示流動方向。圖12為噴管沿-x方向的視圖。沿流動方向空間步進(jìn)400次，步進(jìn)距離為0.318 m，網(wǎng)格量為21×21×400。圖中的軸線、邊界流線、進(jìn)口截面沿j向的網(wǎng)格線，出口截面沿j向的網(wǎng)格線，這四條線共同組成的曲面為流動的流面。從流面的三維特性可以看出，橢圓噴管內(nèi)部存在從y軸向z軸的周向流動。由于初始截面為橢圓，長軸膨脹效率高，膨脹快，為了在周向獲得相同的壓力，長軸的擴(kuò)張角就要小于短軸的擴(kuò)張角，使短軸長度獲得更快的增長速率，因此出現(xiàn)噴管橫截面從橢圓逐漸向圓形過渡的現(xiàn)象。

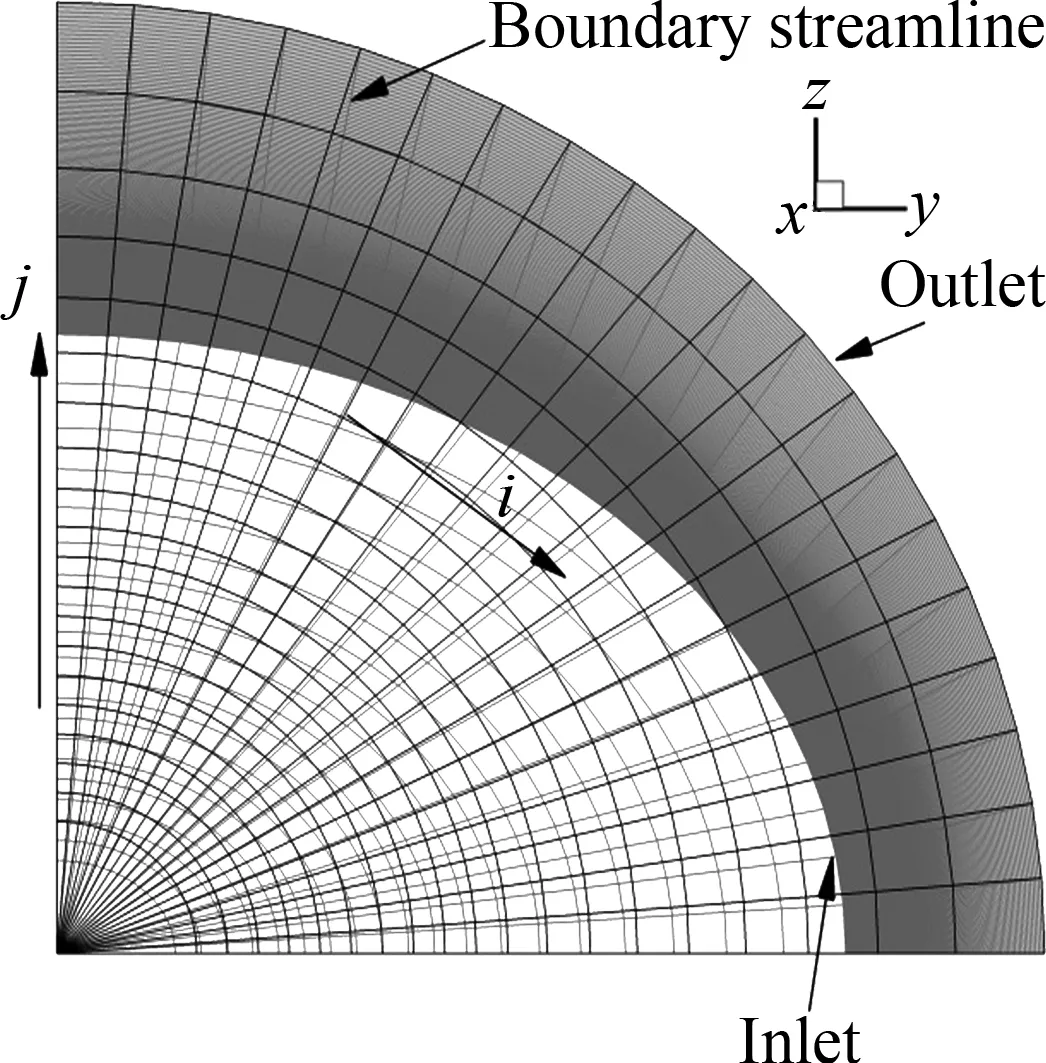
圖12 橢圓形進(jìn)口噴管沿-x方向的視圖Fig.12 View of nozzle with ellipse inlet along -x direction

圖13為截面馬赫數(shù)等值線圖。從圖13中可以看出，橢圓噴管內(nèi)部的馬赫數(shù)等值線均勻平滑，無明顯的膨脹波，具有較高的流場品質(zhì)。

為驗(yàn)證設(shè)計(jì)方法的優(yōu)劣，對橢圓噴管進(jìn)行CFD數(shù)值模擬，將CFD計(jì)算的流場與設(shè)計(jì)的結(jié)果進(jìn)行對比分析。圖14(a)～(d)分別為三維壓力云圖和出口截面的壓力等值線圖、馬赫數(shù)等值線圖，其中CFD計(jì)算得到的等值線為紅色，3D-MOC設(shè)計(jì)流場的等值線為黑色。

為了獲得更加精確地對比，本文分別在設(shè)計(jì)流場和數(shù)值模擬流場的出口截面，提取了沿45°方向的流動參數(shù)，如圖15所示，分別對比了壓力、馬赫數(shù)。可以發(fā)現(xiàn)，在壁面和中心處各項(xiàng)參數(shù)均有不同程度的誤差，但最大相對誤差均為千分之幾量級，甚至為萬分之幾(表2)。

(a) y=0截面

(b) z=0截面圖13 截面的馬赫數(shù)等值線圖Fig.13 Mach number in different sections at y=0 and z=0

圖16分別對比了沿中心線及長短軸壁面的馬赫數(shù)和壓力分布。圖16中可以看出，CFD結(jié)果與設(shè)計(jì)結(jié)果匹配得好，同時(shí)長軸壁面和短軸壁面對應(yīng)的壓力曲線吻合程度高，說明能夠?qū)崿F(xiàn)壁面沿流向的一維壓力分布和一維馬赫數(shù)分布。

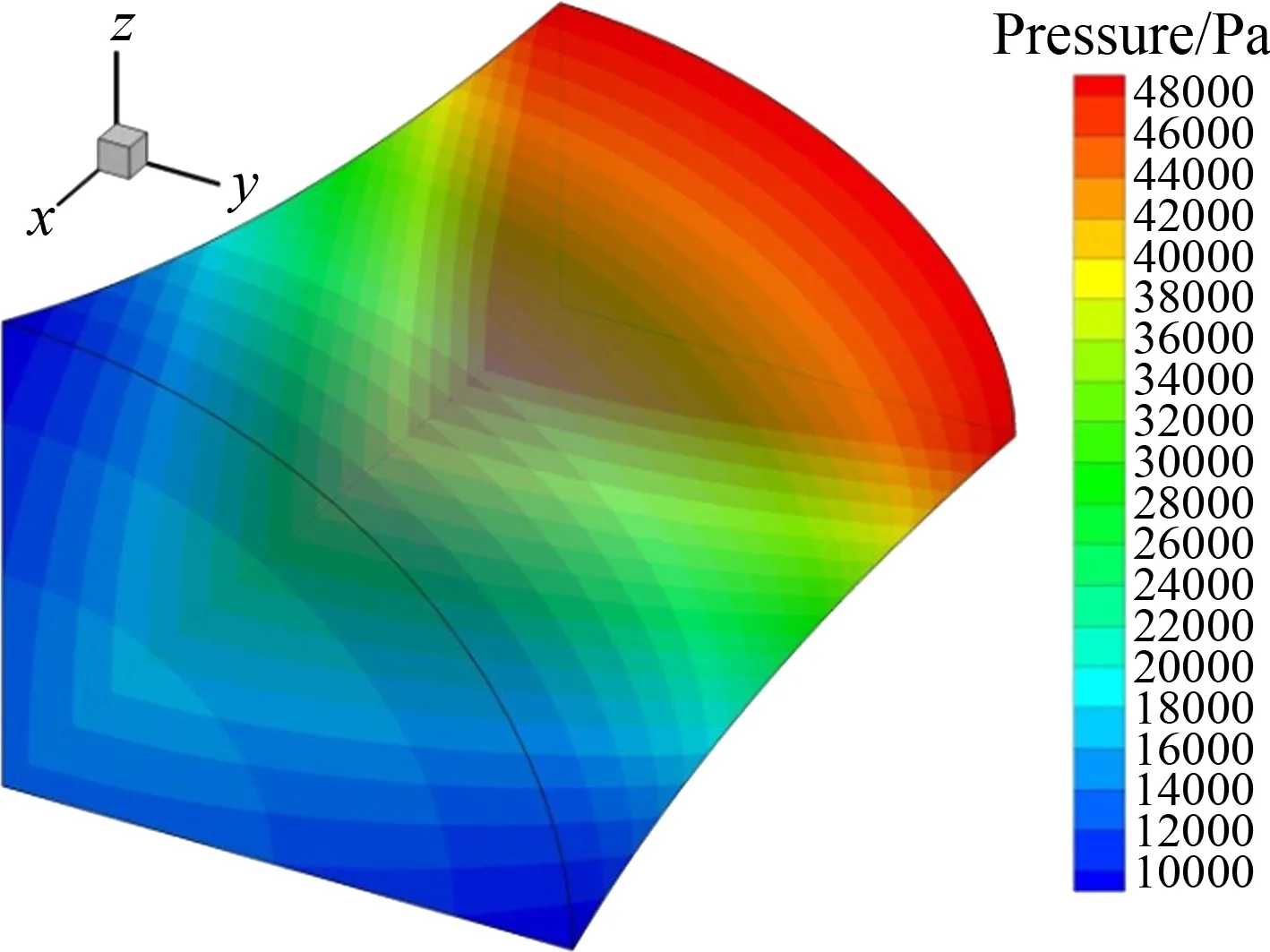
(a) 設(shè)計(jì)流場的三維壓力云圖

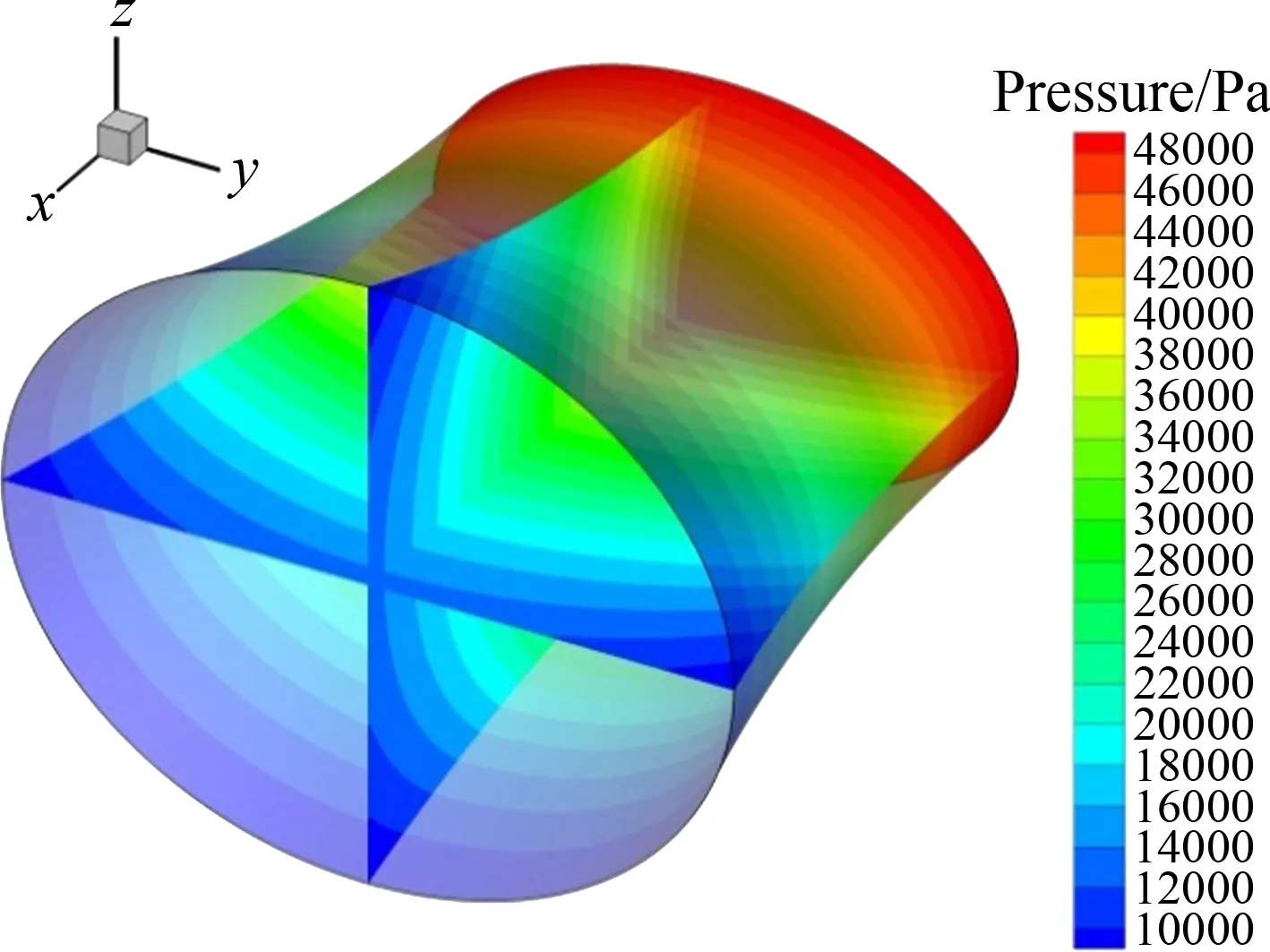
(b) 數(shù)值模擬流場的三維壓力云圖

(c) 壓力等值線對比 (d) 馬赫數(shù)等值線對比圖14 三維壓力云圖及出口截面壓力、馬赫數(shù)的等值線圖Fig.14 Contours of three-dimensional pressure, Mach number and pressure in outlet section

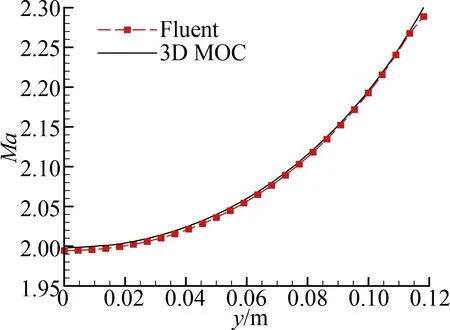
(a) 馬赫數(shù)

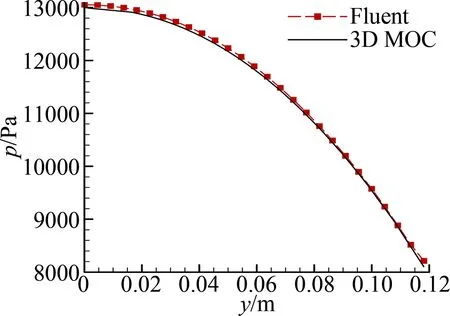
(b) 壓力圖15 出口截面沿45°的馬赫數(shù)分布、壓力分布曲線Fig.15 Comparison for pressure and Mach number along 45° direction in outlet section

(a) 馬赫數(shù)

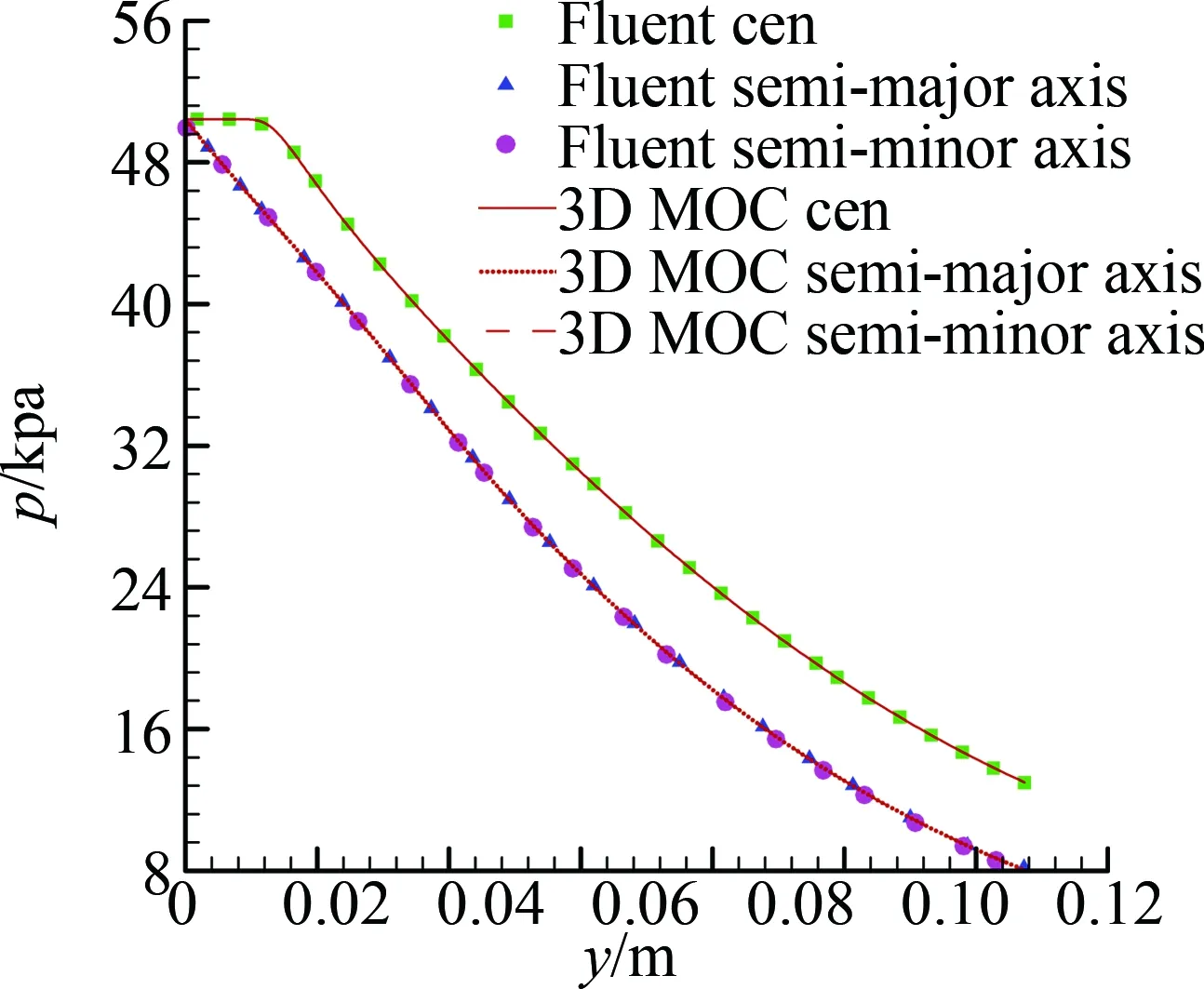
(b) 壓力圖16 沿中心線及長短軸壁面的馬赫數(shù)分布、壓力分布曲線Fig.16 Comparison for pressure and Mach number along central axis, minor axis, and major axis

表2中列出了噴管出口截面與CFD數(shù)值模擬對比的最大相對誤差，由于圓形進(jìn)口的噴管具有較好的軸對稱特性，流動三維特性小，網(wǎng)格的正交性能夠一直保持至出口，因此精度相對較高。而對于橢圓形進(jìn)口，噴管內(nèi)部存在周向流動，網(wǎng)格也隨著流面的扭曲發(fā)生相應(yīng)的扭動，使得網(wǎng)格的正交性略有下降，影響了單元過程中雙線性內(nèi)插的插值精度，同時(shí)該誤差數(shù)值在一定程度上包含了CFD求解的部分誤差，因此誤差相對較大，但是最大相對誤差在千分之幾量級，其設(shè)計(jì)精度仍能夠保證要求。

表2 出口截面各項(xiàng)參數(shù)的最大相對誤差Table 2 Maximal relative error for parameters in outlet section

4 結(jié) 論

綜上所述，基于雙特征線方法的壓力反問題求解技術(shù)具備三維超聲速與高超聲速氣動設(shè)計(jì)的能力，可應(yīng)用于三維超聲速噴管設(shè)計(jì)。該方法未引入任何平面假設(shè)，為純?nèi)S的氣動設(shè)計(jì)方法；最大誤差在千分之幾量級；可通過設(shè)計(jì)壓力進(jìn)行壁面構(gòu)型的設(shè)計(jì)，使得壁面流場參數(shù)控制更加靈活。

在設(shè)計(jì)過程中仍然存在許多問題還有待深入探究，如：流管內(nèi)部的三維激波問題較為復(fù)雜、控制噴管出口形狀需要復(fù)雜的壁面壓力設(shè)計(jì)。因此，還需要繼續(xù)發(fā)展新的技術(shù)來完善該求解技術(shù)。

[1]Yi S H, Zhao Y X, He L, et al.Supersonic and hypersonic nozzle design[M].Beijing: National Defense Industry Press, 2013.(in Chinese)易仕和, 趙玉新, 何霖, 等.超聲速與高超聲速噴管設(shè)計(jì)[M].北京: 國防工業(yè)出版社, 2013.

[2]Zucrow M J, Hoffman J D.Gas dynamics[M].Beijing: National Defense Industry Press, 1984.(in Chinese)左克羅M J, 霍夫曼J D.氣體動力學(xué)[M].北京: 國防工業(yè)出版社, 1984.

[3]Tong B G, Kong X Y, Deng G H.Gas dynamics[M].Beijing: Higher Education Press, 1900.(in Chinese)童秉綱, 孔祥言, 鄧國華.氣體動力學(xué)[M].北京: 高等教育出版社, 1990.

[4]Zhang M L, Yi S H, Zhao Y X.The design and experimental investigation of supersonic length-shorted nozzle[J].Acta Aerodynamica Sinica, 2007, 25(4): 500-503.(in Chinese)張敏莉, 易仕和, 趙玉新.超聲速短化噴管的設(shè)計(jì)與實(shí)驗(yàn)研究[J].空氣動力學(xué)學(xué)報(bào), 2007, 25(4): 500-503.

[5]Ransom V H, Hoffman J D, Thompson H D.A second-order bicharacteristics method for three-dimensional, steady, supersonic flow[J].AIAA Journal, 1972, 10(12): 1573-1581.

[6]Beckel S A, Garrett J L, Gettinger C G.Technologies for robust and affordable scramjet propulsion[R].AIAA 2006-7980, 2006.

[7]Bulman M J, Siebenhaar A.The rebirth of round hypersonic propulsion[R].AIAA 2006-5035, 2006.

[8]Yates L A, Chapman G T.Streamlines, vorticity lines, and vortices around three-dimensional bodies[J].AIAA Journal, 1992, 30(7): 1819-1826.

[9]Billig F S, Kothari A P.Streamline tracing: technique for designing hypersonic vehicles[J].Journal of Propulsion and Power, 2000, 16(3): 465-471.

[10]Lu X, Yue L J, Xiao Y B, et al.Design of scramjet nozzle

based on streamline tracing technique[J].Journal of Propulsion Technology, 2011, 32(1): 91-96.(in Chinese)盧鑫, 岳連捷, 肖雅彬, 等.超燃沖壓發(fā)動機(jī)尾噴管流線追蹤設(shè)計(jì)[J].推進(jìn)技術(shù), 2011, 32(1): 91-96.

[11]You Y C, Liang D W.Design concept of three-dimensional section controllable internal waverider hypersonic inlet[J].Sci China Ser E-Tech Sci, 2009, 52(7): 2017-2028.(in Chinese)尤延鋮, 梁德旺.基于內(nèi)乘波概念的三維變截面高超聲速進(jìn)氣道[J].中國科學(xué): E 輯, 2009, 39(8): 1483-1494.doi: 10.1007/s11431-009-0125-1.

[12]Lu X, Yue L J, Xiao Y B, et al.Design of three-dimensional section controllable scramjet nozzle[C]//The 3th National conference on Hypersonic Technology.2010, Wuxi.(in Chinese)盧鑫, 岳連捷, 肖雅彬, 等.超燃沖壓發(fā)動機(jī)三維變截面尾噴管設(shè)計(jì)[C]//第三屆高超聲速科技學(xué)術(shù)會議, 2010, 無錫.

[13]Smart M K.Design of three-dimensional hypersonic inlets with rectangular-to-elliptical shape transition[J].Journal of Propulsion and Power, 1999, 15(3): 408-416.

[14]Quan Z B, Xu J L, Mo J W.Design and experiment validation of single expansion ramp nozzle based on the control of wall pressure distribution[J].Journal of Propulsion Technology, 2013, 34(3): 307-310.(in Chinese)全志斌, 徐驚雷, 莫建偉.基于控制壁面壓力分布的分級單邊膨脹噴管設(shè)計(jì)及試驗(yàn)驗(yàn)證[J].推進(jìn)技術(shù), 2013, 34(3): 307-310.

[15]Zhao Y X, Liu H Y, Zhao Y L.The inverse problem of the three-dimensional supersonic flow[C]//The 8th National conference on Hypersonic Technology, 2015, Harbin.(in Chinese)趙玉新, 劉紅陽, 趙一龍.三維超聲速流動的反問題[C]//第八屆全國高超聲速科技學(xué)術(shù)會議, 2015, 哈爾濱.

[16]Li Y Q, Han W Q, You Y C, et al.Integration waverider design of hypersonic inlet and forebody with preassigned pressure distribution[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2711-2720.(in Chinese)李怡慶, 韓偉強(qiáng), 尤延鋮, 等.壓力分布可控的高超聲速進(jìn)氣道/前體一體化乘波設(shè)計(jì)[J].航空學(xué)報(bào), 2016, 37(9): 2711-2720.

[17]Zhao Y X, Liu H Y.The characteristic tracing method for supersonic flow field design[C]//The 8th National Conference on Hypersonic Technology, 2015, Harbin.(in Chinese)趙玉新, 劉紅陽.基于特征線追蹤的氣動反設(shè)計(jì)[C]//第八屆全國高超聲速科技學(xué)術(shù)會議, 2015, 哈爾濱.

[18]Liu H Y.The characteristics tracing method and its applications[D].National University of Defense Technology, 2015.(in Chinese)劉紅陽.特征線追蹤方法和應(yīng)用[D].國防科技大學(xué), 2015.

[19]Liu H Y, Zhao Y X.Design of three-dimensional supersonic flow based on the characteristics tracing method with circle -to-rectangular shape transition.[C]//The Chinese Congress of Theoretical and Applied Mechanics, 2015, Shanghai.(in Chinese)劉紅陽, 趙玉新, 基于特征線追蹤的三維圓轉(zhuǎn)方超聲速流道設(shè)計(jì)[C]//中國力學(xué)大會, 2015, 上海.

[20]Ransom V H, Hoffman J D, Thompson H D.A second-order numerical method of characteristics for three-dimensional supersonic flow[D].Purdue University, 1970.

[21]Cline M C, Hoffman J D.Comparison of characteristic schemes for three-dimensional, steady, isentropic flow[J].AIAA Journal, 1972, 10(11): 1452-1458.

Pressure inverse problem of three-dimensional supersonic flow

LAN Qingsheng1, ZHAO Yuxin1,*, ZHAO Yilong1, LIU Hongyang2

(1.ScienceandTechnologyonScramjetLaboratory,NationalUniversityofDefenseTechnology,Changsha410073,China;2.ComputationalAerodynamicsInstitutesofChinaAerodynamicsResearchandDevelopmentCenter,Sichuan621000,China)

In order to explore valid methods for three-dimensional supersonic flow design, a technology was proposed to solve the pressure inverse problem by finding inviscid contour on the basis of a preassigned pressure distribution along the wall.A bicharacteristic algorithm is used to solve the inverse problem.Three-dimensional wall coordinates can be calculated directly according to the flow condition and predetermined boundary pressure.The designed three-dimensional contour can be compatible with preassigned pressure distribution by moving forward the solution plane along thexcoordinate.The accuracy order of the solver was tested by comparing numerical solutions with analytical results of Prandtl-Meyer expansion wave.Three-dimensional supersonic nozzles with round or oval inlet were designed in this paper on the basis of one-dimensional pressure distributions.The reliability of the solver was validated by corresponding CFD numerical simulations.It can be found that the numerical solutions of the present solver are in good agreement with those of CFD simulations.The solver has the ability for three-dimensional supersonic aerodynamic design by solving the inverse problem based on the bicharacteristics method.Moreover, this solver has advantages of high accuracy, pure three-dimensional solutions, and controllable wall pressure distribution.The method has promising potential of playing a supporting role in the applications of further hypersonic aerodynamic design.

pressure inverse problem;bicharacteristics method;three-dimensional supersonic aerodynamic design;controllable wall pressure distribution

0258-1825(2017)03-0429-07

2016-12-02;

2017-01-11

國家自然科學(xué)基金(11472304)

藍(lán)慶生(1992-),男(畬族),福建龍巖人,碩士研究生,研究方向:高超聲速氣動設(shè)計(jì).E-mail:lanqingsheng2015@163.com

趙玉新*(1980-),男(滿族),吉林舒蘭人,教授,研究方向:高/超聲速氣動設(shè)計(jì)、超聲速邊界層、超聲速流動成像測量等.E-mail:zyx_nudt@163.com

藍(lán)慶生, 趙玉新, 趙一龍, 等.三維超聲速流動的壓力反問題[J].空氣動力學(xué)學(xué)報(bào), 2017, 35(3): 429-435.

10.7638/kqdlxxb-2016.0156 LAN Q S, ZHAO Y X, ZHAO Y L, et al.Pressure inverse problem of three-dimensional supersonic flow[J].Acta Aerodynamica Sinica, 2017, 35(3): 429-435.

V434+.1

A doi: 10.7638/kqdlxxb-2016.0156