向量知識在橢圓中的滲透
2017-07-05 12:57:20廣東省開平市教倫中學劉世洪
中學生數(shù)理化(高中版.高考數(shù)學) 2017年4期
■廣東省開平市教倫中學 劉世洪
向量知識在橢圓中的滲透
■廣東省開平市教倫中學 劉世洪
向量知識與圓錐曲線的交匯問題已成為高考的熱點問題。在平時的學習中就應當注意并積累這一熱點問題的各種解法。橢圓方程是圓錐曲線中的一種重要曲線方程,在學習橢圓時,我們就要把向量與橢圓的交匯問題作為一個重要的題型來研究與學習。
一、向量知識背景下的線段的定比分點問題在橢圓中的滲透
(Ⅰ)求橢圓方程;

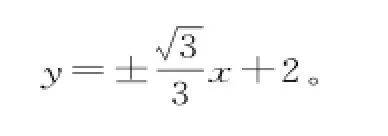
點評:題設條件中出現(xiàn)有向線段所成的比,實際上是告訴我們一個向量方程,如果向量方程中的向量為坐標表示,那么就為我們提供了一個求值的條件。因為未知數(shù)的求解都是要通過方程來確定,而且向量方程為我們提供的是兩個代數(shù)方程,因為向量方程等號兩邊的向量的橫、縱坐標都要相等。就像該題由向量方得(-x1,2-y1)=2(x2,y2-2),于是獲得兩個代數(shù)方程-x1=2x2與2-y1=2y2-4。
二、共線向量與橢圓問題的交匯

三、向量數(shù)量積在橢圓中的滲透

(責任編輯 王福華)
由②③⑤得3m2=b2。 ⑥
由④⑥解得b2=3,m=±1適合①式。
故所求直線l的方程為y=x+1或y=x-1;橢圓C的方程為
點評:若點P、Q的坐標分別為P(x1, y1),Q(x2,y2),則向量數(shù)量積的坐標表示為就像該題的題設條件一樣,如果告訴我們向量數(shù)量積的值為-3,則我們就可以通過該數(shù)量積建立方程x1x2+y1y2=-3,從而為下面的求值問題創(chuàng)造條件。
 中學生數(shù)理化(高中版.高考數(shù)學)2017年4期
中學生數(shù)理化(高中版.高考數(shù)學)2017年4期
- 中學生數(shù)理化(高中版.高考數(shù)學)的其它文章
- 電磁感應第二輪復習檢測題
- 圓錐曲線錯點多 審題求解細斟酌
- 圓錐曲線重要考點分析
- 突破有機物制備實驗
- 透過細節(jié)看有機化學新考法
- 圓錐曲線中如何解決參變量的取值范圍
