融資約束下CPPI策略風險分析

丁釗鵬，劉立新

（1.對外經貿大學金融學院，北京100029；2.北京聯合大學，北京100101）

融資約束下CPPI策略風險分析

丁釗鵬1,2，劉立新1

（1.對外經貿大學金融學院，北京100029；2.北京聯合大學，北京100101）

在融資約束之下，通過定義三種資產狀態，文章計算出投資組合價值在三者之間的轉移概率矩陣，并推演出各概率值與風險乘數、資產波動率、期望收益率、無風險收益率和投資者風險偏好諸要素之間的增減關系。以滬深300指數作為風險資產，在四類典型波動的市場，推算出融資約束下不同調整周期與風險乘數對應的期末組合價值以及各狀態的期初期末轉移概率，并闡述了市場狀況與投資組合保險策略的選擇關系以及風險頭寸與組合保險失敗的聯系。

投資組合保險；風險乘數；融資約束；轉移概率

0 引言

投資組合保險策略，即投資機構在保障資金安全的前提下，在各資產類別之間動態線性配置投資資金比重，以期獲得較高的市場收益率。

對于投資組合策略，一個基本的前提假設是：可用資金量不存在任何限制。但在CPPI策略中，倘若風險乘數過大，隨著市場的變化，一定時期，風險資產投資額度理論上可能會高于當期投資組合價值總額，因此，當期資產不但悉數應投向風險資產，尚且需要借助外部融資杠桿投向風險資產。然而對于很多基金來說，融資約束通常存在，甚至不允許外部杠桿借貸，況且，即使不存在融資約束，過高的杠桿融資成本也將使多數投資者望而卻步。本文擬在融資約束之下，通過定義三種資產狀態，利用轉移概率矩陣，推演出各概率值與風險乘數、資產波動率、期望收益率、無風險收益率和投資者風險偏好諸要素之間的增減關系，在融資約束下，以滬深2011—2014年四個有代表性的風險市場推算出不同調整周期與風險乘數所對應的期末組合價值以及各狀態的期初期末轉移概率，并闡述了市場狀況、風險頭寸與組合保險策略選擇之間的內在關聯。

1 融資約束下的條件轉移概率

策略的基本理論公式和符號：

Vt:t時刻投資組合價值；

Ct:t時刻緩沖值；

Ft:t時刻要保額度；

Et:t時刻風險資產投資價值；

St:t時刻風險資產市場價格；

Dt:t時刻無風險資產市場價格；

G:投資者要求的期末要保額度價值；

m:風險乘數；

r:即期無風險收益率。

按照CPPI策略，投資者根據風險偏好在期初設定風險乘數m以及t時刻所需要保額度Ft，風險資產投資額度為風險乘數乘以緩沖值Ct=Vt-Ft，余下份額投向無風險資產。隨著市場上風險資產價格的變動以及投資保險期限逐步收縮，風險資產與無風險資產二者之間的投資權重需要投資者動態調配。此處的風險乘數（m＞1）對應于投資者的金融杠桿，越高的風險乘數，代表投資者越風險偏好，投資者在風險資產升值中具有更誘人的杠桿收益；反之，一旦風險資產下跌，則投資組合價值損失成倍放大，在來不及重配資產并止損的情況下，投資組合將無從保險。

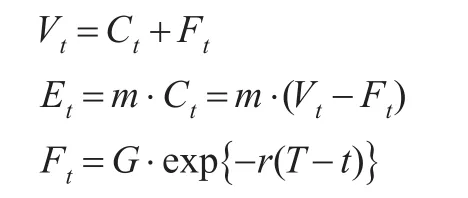
定理1：按照Black-Scholes的假設，且無風險資產收益率、風險資產漂移率及波動率和都是固定值，可得投資組合價值將滿足：

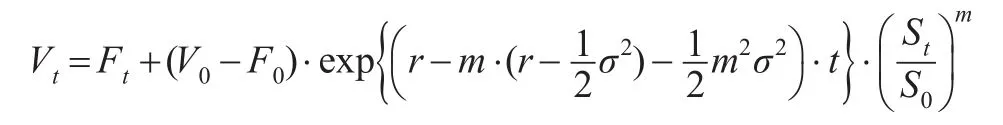
倘若存在融資約束，即投資者投資于風險資產的頭寸受到外部融資的限制，那么風險資產頭寸將定義為：

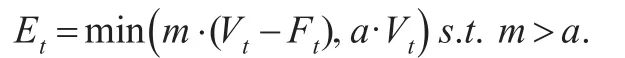
其中，a表示當期組合價值用于風險資產頭寸的上限比率，它刻畫了投資者的風險偏好程度。則可以得到，在任意投資組合調整周期Δt=ti-ti-1內，總是存在三種不同的投資組合價值狀態：

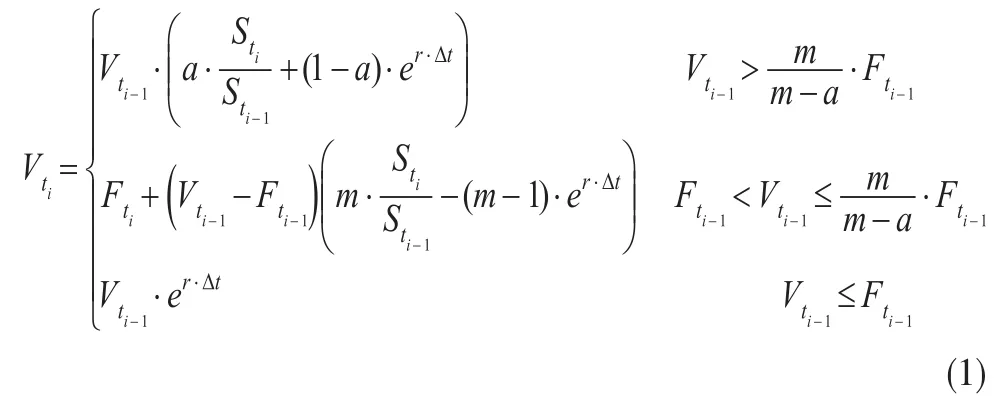
定理2：從ti-1至ti這段時間區間，投資組合價值三種狀態之間存在一定的轉移概率，且令條件轉移概率矩陣為：

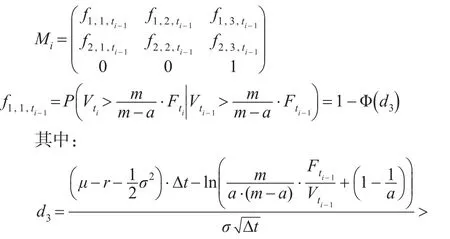
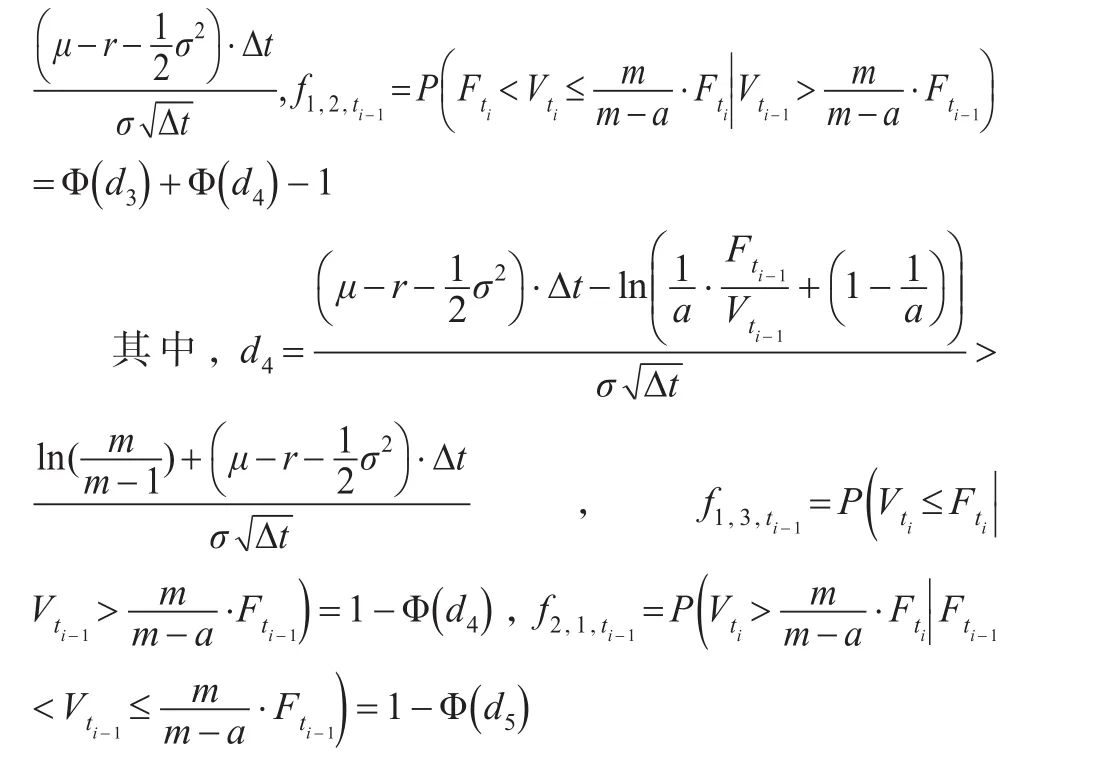
其中：

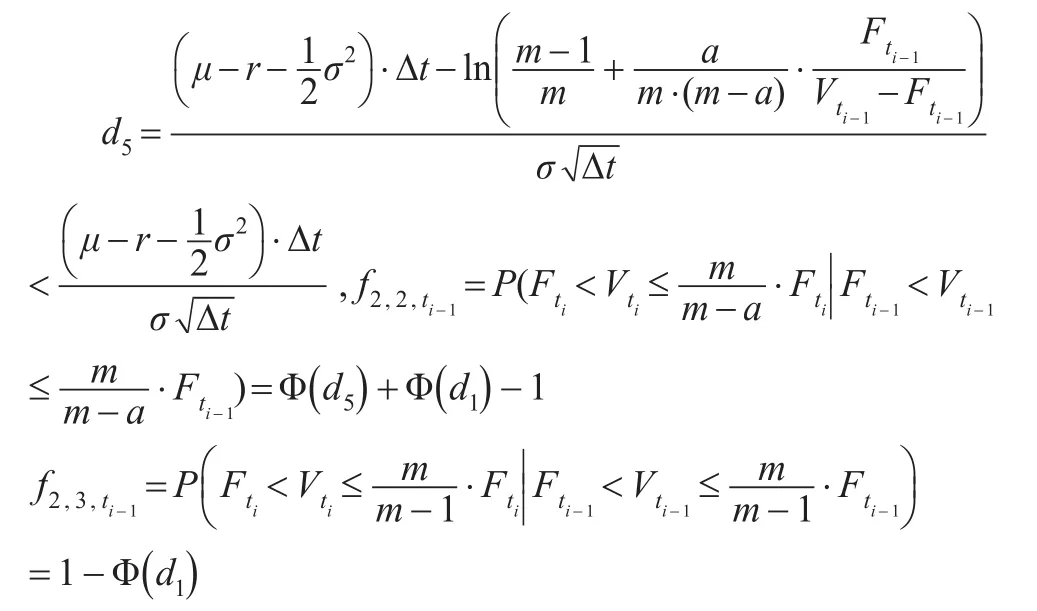
推論1：條件轉移概率矩陣：

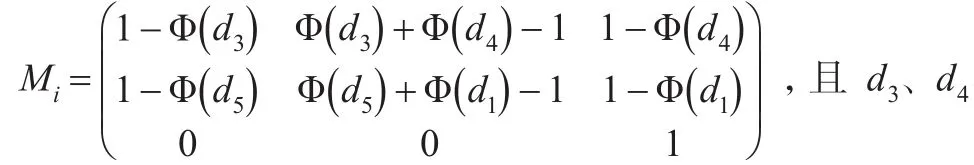
d5皆依賴于該時間區間內期初要保額度與投資組合價值

且由上面分析可知：d4＞d1＞d3＞d5，因此

上面的不等式表明：當前一期投資組合價值超過要保額度時，下一期超過投資上限限額（轉移至狀態1）的概率必將大于不能保底的概率（轉移至狀態3），亦即，無論取什么樣的參數，當期保險失敗的條件概率永遠不可能超過50%。

由d1、d3、d4、d5各自的定義，將之關于m、σ、μ、諸因素進行相應的敏感度分析，可以得到相互之間的增減關系如表1所示：

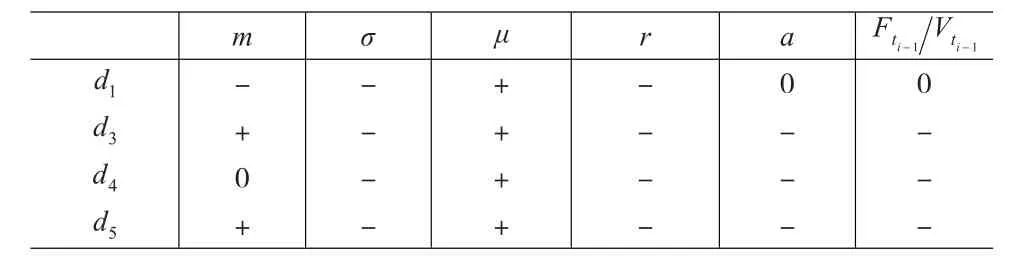
表1 各因素對d1、d3、d4、d5的影響

結合條件轉移概率的定義，可以得到各概率值與相應要素之間的關系如下頁表2所示。

表2 各因素對轉移概率的影響

推論2：從表2可以看出：隨著風險乘數m的增大，狀態1與狀態2能夠保持或上升到狀態1的概率減少，雖然狀態1跌至狀態3的概率未變，但是狀態2跌至狀態3的概率卻上升了，因此，風險乘數若增加，缺口風險將會上升。

隨著風險資產波動率σ的增大，狀態1與狀態2保持之前狀態的概率均減少，但是轉移至狀態1與狀態3的概率均有所增加，因此波動率使得未來的走向變得更加的不確定：或者更好，或者更壞。這并非單由波動率可以決定，總體上說，波動率若增加，缺口風險會上升。

隨著風險資產漂移率μ的增加，與波動率σ的作用恰好相反，它會使得投資組合價值向狀態2集中，轉移向狀態1與狀態3的概率皆會縮小，從而價值狀態越趨穩定，漂移率若增加，缺口風險會減少。

隨著無風險資產收益率r的增加，與風險資產漂移率μ的作用恰好相反，它會使得投資組合價值以更大的概率向狀態1與狀態3轉移，而狀態2的概率減少。原因在于，無風險收益率是要保額度的增長率，也是風險資產的機會成本，所以無風險收益率若增加，缺口風險會增加。

隨著融資約束比率a的增加（限制減弱），則向上的收益空間更大，亦即向狀態1轉移的概率增大，從而降低了投資組合價值在狀態2中的概率，但是由于杠桿交易的作用同時也放大了從狀態1陡然下降到狀態3的概率，因此，融資約束比率若增加，缺口風險會上升。

a，故效果與之相似，投資更激進，缺口風險也會更大。

推論3：令ti時刻的非條件狀態概率分別如下：

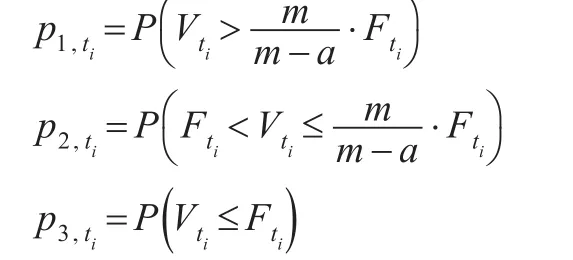
由上面的分析可知，該狀態概率是路徑依賴的

2 融資約束下CPPI策略實證分析

風險資產采用滬深300指數，圖1為該指數2011—2014年的走勢。

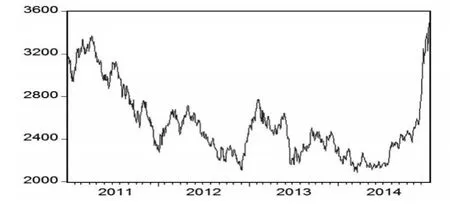
圖1 滬深300質素2011—2014年走勢圖

2011 年，滬深市場處于跌勢，日最大跌幅達到3.87%；2012年，滬深市場震蕩中收漲，日最大跌幅達到2.88%；2013年，滬深市場震蕩中收跌，日最大跌幅達到6.52%；2014年，滬深市場處于漲勢，日最大跌幅達到4.59%。選取這四年作為實證的原因，即在于這四年的滬深市場囊括了具有代表性的四類風險資產波動類別。以一年作為組合投資期限，進行不同市場的比較實證，無風險收益率則參考一年期國債收益率。

期初，假定組合價值為100，并以期初組合價值的90%作為期末的要保額度，亦即G=90。滬深股票交易是按成交金額的千分之三收取傭金，并按成交金額的千分之一收取印花稅，實證中假定風險資產換手金額的千分之四作為總交易費。

在不可融資限制下（a=1），以0.025為間隔選擇風險乘數m∈(1，10]，選擇組合調整周期△t=1，5，10，20，30，40（分別對應日、周、兩周、四周、六周、八周），可以得到2160種組合。

可以計算出不可融資限制下不同調整周期與風險乘數對應的期末組合價值，如圖2所示：

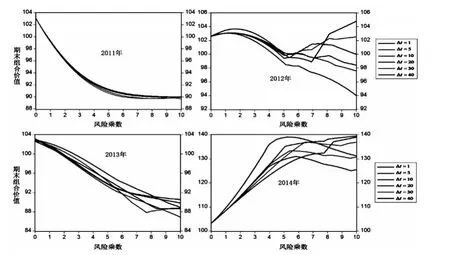
圖2 不可融資條件下期末組合價值

從最低期末組合價值比較可見，在市場下跌或震蕩收跌之時，不可融資的限制并未保證投資組合保險的成功。

根據圖2，可以得到不可融資限制下最優的風險乘數和調整周期，如表3所示：

表3 不可融資限制下最優的固定風險乘數和調整周期

若存在外部融資約束，在下跌或震蕩收跌的市場，最好避免投資風險資產；而對于上漲或震蕩收漲的市場，最優策略卻是選擇較高的風險乘數和較長的調整周期。較高的風險乘數可以通過較大的權重投資于風險資產從而獲得較多的風險收益率，而較長的調整周期則可以最大程度上避免因頻繁換手對應的波動回調和交易費用對于收益的吞噬。

同時，在不可融資限制下，以0.025為間隔選擇風險乘數m∈(1，10]，選擇△t=1，5，10，20，30，40，可以得到2160種組合，按之前的定義，組合價值的三種狀態依次為：狀態1、狀態2、狀態3，從而計算得到各狀態的初始概率與轉移概率如表4所示：

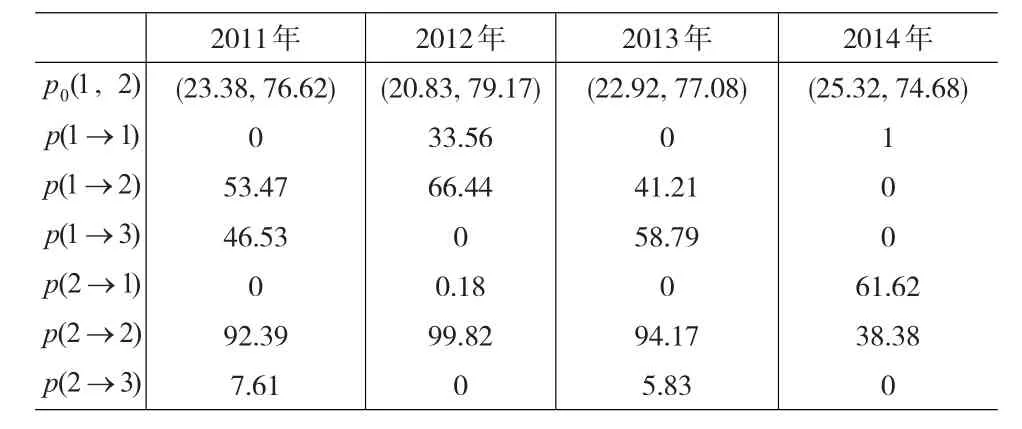
表4 初始概率與轉移概率的計算結果（單位：%）

由表4可知：在下跌的市場（2011年）或震蕩收跌的市場（2013年），轉移概率相似，如果初始組合價值處于狀態1，期末將有一半的概率跌到狀態2，另一半概率跌到狀態3（保險失敗），如果初始組合價值處于狀態2，則期末基本會維持在狀態2；在震蕩收漲的市場（2012年），如果初始組合價值處于狀態1，將有約1/3的概率期末維持狀態1剩下2/3的概率跌到狀態2，如果初始組合價值處于狀態2，則基本會維持在狀態2；而在上漲的市場（2014年），若初始組合價值處于狀態1，期末將會維持在狀態1，若初始組合價值處于狀態2，則將有約1/3的概率維持在狀態2還有2/3的概率期末上升至狀態1。

由計算可知，只要風險乘數大于7.9左右，則初始狀態就位于狀態1，它代表了使用了較高的金融杠桿，從而放大了風險頭寸。金融杠桿的使用，在震蕩收漲的市場（2012年）與上漲的市場（2014年）中可以保障本金安全前提下能取得較好的投資績效。然而，在下跌的市場（2011年）或震蕩收跌的市場（2013年）中高金融杠桿卻可能導致組合保險失敗。

因此，投資失敗的主要原因是在市場下跌或震蕩下跌的情況下決策者過于激進的風險偏好并選擇了過高的風險乘數，從而放大了保險失敗的缺口風險。

對于投資者來說，市場的趨勢是投資組合保險失敗與否的重要因素。但是無論什么樣的市場，過度的風險頭寸都是投資組合保險失敗的誘因，尤其在預期下跌或震蕩收跌的市場，風險乘數的設定存歿攸關。

3 結論

在存在融資約束之下，本文計算出投資組合價值在三種資產狀態之間的轉移概率矩陣，并推演出：風險乘數若增加，缺口風險將會上升；波動率若增加，缺口風險會上升；漂移率若增加，缺口風險會減少；無風險收益率若增加，缺口風險會增加；融資約束比率若增加，缺口風險會上升；若增加融資約束比率，投資更激進，缺口風險也會更大。

本文利用滬深300指數在2011—2014年這四個典型波動年份數據，計算出不可融資限制下最優的風險乘數和調整周期，從而為市場狀況與投資組合策略的選擇提供了實證參考。通過這四年的金融數據實證計算出不同初始狀態的期末資產價值轉移概率，從中可知，組合保險失敗的主要原因是在市場下跌或震蕩下跌的情況下決策者過于激進的風險偏好從而選擇了過高的風險乘數，過度的風險頭寸導致了保險失敗。

[1]Black F,Jones R.Simplifying Portfolio Insurance[J].Journal of Portfolio Management,1987,14,(1).

[2]Merton R C.Continuous-Time Finance[M].New York:Basil Blackwell,1990.

[3]Black F,Andre F.Theory of Constant Proportion Portfolio Insurance [J].Journal of Economic Dynamic and Control,1992,(16).

[4]Khuman A,Dietmar M,Nick C.Constant Proportion Portfolio Insurance:Statistical Properties and Practical Implications[R].University of Essex,Working Paper,2008.

[5]Weng C G.Constant Proportion Portfolio Insurance Under a Regime Switching Exponential Levy Process[J].Insurance:Mathematics and Economic,2013,(52).

[6]程兵，魏先華.投資組合保險CPPI策略研究[J].系統科學與數學，2005，25(3).

[7]杜少劍,陳偉忠.CPPI投資組合保險策略的實證分析[J].財貿研究，2005，(1).

[8]黃麗清.CPPI策略缺口風險研究[D].上海：復旦大學，2009.

[9]徐競.基于馬爾科夫鏈的動態CPPI投資策略研究及實證[J].重慶理工大學學報：自然科學版，2012，26(4).

[10]周圣，史本山，段玉娟.基于離散時間交易下的CPPI策略[J].系統工程，2012，30(5).

（責任編輯/易永生）

F832

A

1002-6487（2017）11-0162-04

丁釗鵬（1978—），男，四川潼南人，博士研究生，講師，研究方向：金融工程、債券及衍生品。劉立新（1966—），男，河北安國人，教授，博士生導師，研究方向：金融工程、風險管理。