“物質的量”概念難點成因分析及教學建議
喬靜
“物質的量”是高中化學必修1中一個非常重要的概念,它是連接微觀與宏觀、定性與定量的橋梁,貫穿于高中化學知識學習的始終。然而,由于“物質的量”這一概念抽象難懂,在實際教學中又與“摩爾”“阿伏加德羅常數”等以概念群的形式出現,使得教師難教、學生難學。
一、“物質的量”概念成為教學難點的原因分析
“物質的量”成為教學難點,從以下三個方面分析原因。
1.與“物質的量”相關知識與技能繁雜,難度較大
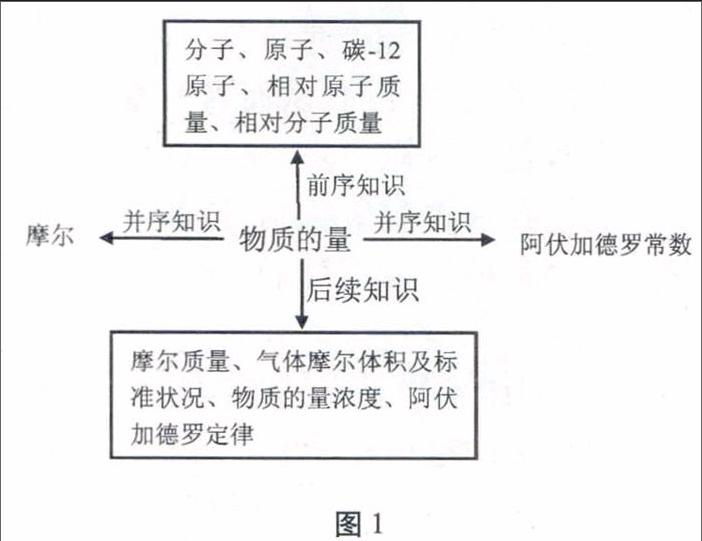
“物質的量”學習的前序知識有分子、原子、質量、碳一12原子、相對原子質量、相對分子質量等;并序知識有“摩爾”“阿伏加德羅常數”;后續知識有“摩爾質量”“氣體摩爾體積及標準狀況”“物質的量濃度”“阿伏加德羅定律”等(見圖1)。
化學技能方面,化學式、化學方程式的書寫與計算不僅是“物質的量”概念學習的基礎,而且是深入理解概念的重要手段和有效途徑。以“物質的量”為核心的計算是高中學習的重點和難點,是高中階段乃至大學繼續學習化學的基礎性知識和能力。
因此,與“物質的量”相關的概念和知識抽象、難懂,教學中又以概念群的形式密集出現,產生疊加效應,加大了“物質的量”的學習難度。
2.學生認知能力的局限
初中階段化學學習是以“質量”為核心的定量系統,而“物質的量”相關概念對于剛升上高一的學生來說是一個全新的定量系統。
“質量”是宏觀層面的,是學生日常生活中經常接觸到的物理量;“物質的量”是微觀層面的,是一個將質量、體積等宏觀物理量與原子數、分子數等微粒世界聯系起來的物理量,對抽象思維要求較高,認知發展水平仍處于具體運算階段的學生很難將宏觀與微觀聯系起來。
3.教材中概念的呈現方式不利于學生理解
“物質的量”一詞在漢語的語法分析中是一個偏正短語,中心詞是“量”。究竟是什么量,是我們熟知的質量、長度、體積嗎?概念十分模糊,這在某種程度上加大了概念理解的難度。
“物質的量”對應的英文是“amount of sub-stance”,中心詞是“amount”意為“數量、總數、總額”。在英語中“物質的量”的意義是明確的,就是指的數量。而在翻譯過程中,直接譯為“量”這一籠統模糊的字,給學生理解概念造成了困難。
沈仁義教授建議將“物質的量”改為“物質的微粒數”,這一提法的字面意義明確,不僅解釋了“量”即“數量”,而且指明了這個數量只能表示微觀粒子,不能表示宏觀物質,從而高度概括了“物質的量”這一物理量的基本含義。
二、“物質的量”概念的教學建議
人教版高中化學必修1呈現“物質的量”概念群的順序:先介紹“物質的量”,而“摩爾”是作為“物質的量”的單位被直接引出的,阿伏加德羅常數則是解釋1mol粒子集體所含的粒子數,約為6.02×1023。
按照這樣的方式進行教學,無疑是生硬地將幾個概念的疊加灌輸給學生,學生很難將知識內化,死記硬背概念成了大多數學生學習的現狀。這與改變過去接受式學習、死記硬背、機械訓練,倡導學生主動參與、樂于探究、自主建構的新課程理念背道而馳。
筆者建議應由較好理解的“摩爾”引出“物質的量”概念,淡化并延后“阿伏加德羅常數”的教學。具體教學過程如下。
1.情境創設
教師播放《曹沖稱象》的Flash短片,引導學生思考“這個故事中主人公曹沖是如何聰明地化解生活中的一些‘難題,主要利用了什么思想?”
學生分析之后得出結論:“化整為零”的思想。
[教師小結]曹沖就是將難以稱量的大象重量轉化為相對較小的可稱量的石頭的重量,化整為零進行稱量的。
教師引導學生再思考,“我們能不能用手中的直尺測量出一張紙的厚度呢?”
[學生]當然不能,直尺的精確度不夠。
[教師追問]那如何破解這個難題?(進一步激化矛盾)
[學生]我們可以測量出整十張、整百張紙的厚度,然后再除以紙張數……
[教師追問]這個過程中又利用了什么思想?(“化零為整”的思想呼之欲出,為“物質的量”概念的形成掃清了障礙)
2.類比“摩爾”概念
[教師總結]“曹沖稱象”的思想是化整為零,而我們測量一張紙的厚度又是利用化零為整的思想。我們不是直接測量一張紙的厚度,而是把一定數量的紙變為一個“集合體”后再測量……
[教師]其實生活中會經常使用很多這樣類似的集合體名詞。比如一雙(2個)襪子、一打(12個)雞蛋、一筐石頭、一包餐巾紙、一火車皮物資等等。
[總結]“集合體”在生活中時常使用,它給計數帶來了便利。
[過渡]化學是在分子、原子層面上進行的研究,分子和原子都是非常微小的,肉眼是無法辨別的。
[PPT展示]人教版初三化學教材“分子和原子”中的一部分內容:1個水分子的質量約是3×10-26。kg,1滴水中大約有1.67×1021。個水分子。如果10億人來數一滴水中的水分子,每人每分鐘數100個,日夜不停,需要3萬年才能數完。
由此可見,原子、分子等微粒的數目是巨大的,在計數過程中一個一個數是不可取的。
[追問]那么是否可以利用“集合體”的形式來表示呢?(此時,“摩爾”的概念水到渠成。)
[教師]因此在化學上引入“摩爾”概念,我們將“0.012kg12c中所含的碳原子數”這個集合體規定為1mol,通過精密的計算約為6.02 x1023,稱為阿伏加德羅常數(這里可以淡化阿伏加德羅常數的介紹,以突出“摩爾”概念的教學)。
3.引出“物質的量”概念
在理解了“摩爾”是表示物質微粒個數的單位,對“物質的量”即物質所包含微粒的數量的理解便迎刃而解了。
需要注意的是:“物質的量”僅是對于微觀粒子而言的,不能表示宏觀物質。
4.“阿伏加德羅常數”教學
“阿伏加德羅常數”是學生理解的又一難點,給“摩爾”和“物質的量”的學習帶來了極大障礙。實際上,教材中回避使用“阿伏加德羅常數”,并不會影響學生對粒子集合體的理解。回避或延后“阿伏加德羅常數”概念的教學可以有效降低“物質的量”概念群的理解難度。筆者建議,可以將其延后一個課時以補充材料的形式對“阿伏加德羅常數”進行講解。
“物質的量”概念的教學歷來是高中化學學習的重點和難點,在實際教學中,采用先通過生活中的實例類比“摩爾”概念,在此基礎上引出“物質的量”,將“阿伏加德羅常數”的教學延后一課時以補充材料的形式加以介紹,大大化解教學難點,使學生更好理解和學習“物質的量”概念群。

