基于Rayleigh—Sommerfeld積分的矢量衍射理論的適用范圍

王曉琨+耿滔

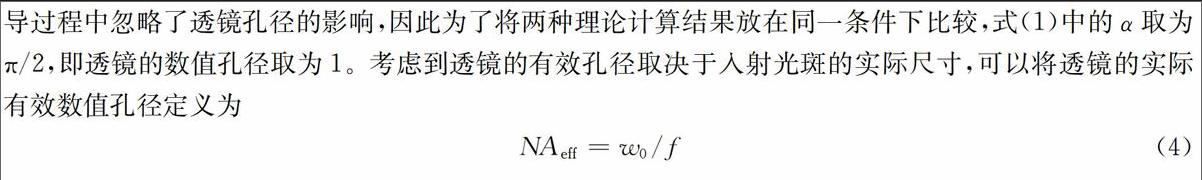
摘要： 以徑向偏振的Laguerre-Gaussian光束為例，探討了基于Rayleigh-Sommerfeld積分的矢量衍射理論的適用范圍。經與Richards-Wolf理論計算結果比較發現，在有效數值孔徑小于0.4的情況下，Rayleigh-Sommerfeld理論可以適用，并可用于探討小菲涅耳數的焦移問題。但對于緊聚焦大數值孔徑系統，Rayleigh-Sommerfeld理論不再適用，因為這種理論低估了光波的衍射效應和矢量性，使得計算所得的聚焦光斑尺寸偏小。

關鍵詞： 矢量衍射； Rayleigh-Sommerfeld積分； 徑向偏振

中圖分類號： O 436.1 文獻標志碼： A doi： 10.3969/j.issn.1005-5630.2017.03.005

Application of the vector diffraction theory based on

Rayleigh-Sommerfeld integration

WANG Xiaokun1，2，3， GENG Tao1，2，3

（1.Shanghai Key Laboratory of Modern Optical System， University of Shanghai for Science and Technology， Shanghai 200093， China；

2.Engineering Research Center of Optical Instruments and Systems（MOE），University

of Shanghai for Science and Technology， Shanghai 200093， China；

3.School of Optical-Electrical and Computer Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：

The application of the vector diffraction theory based on Rayleigh-Sommerfeld integration has been studied using Laguerre-Gaussian beams with radial polarization.It is found that the Rayleigh-Sommerfeld vector diffraction theory is valid when the numerical aperture is less than 0.4 in comparison with the calculation results of Richards-Wolf vector diffraction theory.However，for short-focus large-numercial-aperture systems，the Rayleigh-Sommerfeld theory underestimates the diffraction effect and the vector property of light waves.Thus，the Rayleigh-Sommerfeld theory cannot be used for short-focus large-numercial-aperture systems.

Keywords： vector diffraction； Rayleigh-Sommerfeld integration； radial polarization

引 言

由于緊聚焦光束的焦斑很小及特殊的焦場特性，使得其在半導體光刻、顯微成像、光學加工及微操縱等領域有極其重要的應用。因此緊聚焦光束的研究已經成為國際和國內熱門的研究領域之一。

根據光學成像原理，小數值孔徑系統滿足傍軸近似條件，光束可用標量來表示，此時光束近場和遠場復振幅之間的聯系可以由傅里葉變換來描述。在這種情況下，通常使用菲涅耳衍射理論加上理想薄透鏡的相位變換公式來分析成像系統。而對緊聚焦大數值孔徑系統，傍軸近似條件不再適用，同時光束的矢量特性不能再被忽略。探討矢量衍射的方法有很多，目前被廣泛接受的理論是由Richards和Wolf提出的基于德拜近似的平面波角譜展開法[1-2]，但這種方法由于使用了德拜近似，因此對小菲涅耳數系統不適用，無法探討焦移問題[3]。近年來，有學者提出了基于Rayleigh-Sommerfeld（R-S）積分的矢量衍射方法[4-5]，并認為這種方法可以研究離軸緊聚焦系統，且與Richards-Wolf（R-W）方法相比有兩個顯著的優點，一是可用于小菲涅耳數系統探討焦移現象，二是這種方法可以獲得緊聚焦條件下Laguerre-Gaussian光束低階模式的解析解。

然而基于R-S積分的矢量衍射方法是否可以運用于緊聚焦系統，以及是否有使用限制、限制范圍等問題目前還沒有詳細的研究報道。本文將對其進行研究，考慮到徑向偏振是最適合產生超分辨光斑的偏振態[6-7]，本文將以徑向偏振光為例，探討R-S理論的使用范圍。

1 矢量衍射理論

在R-W理論的框架下，當入射光為徑向偏振時，經理想透鏡聚焦后的電場分布可以表示為[8]

式中：ρ、φ、z分別為衍射場的徑向、角向和縱向的坐標；α為最大半孔徑，α=arcsin（NA），NA為透鏡的數值孔徑；θ為孔徑角；k為波矢，且k=2πλ；A為常系數；Jm為m階貝塞爾函數；l0（θ）為入射光的振幅分布。在本文中取最低階的Laguerre-Gaussian光束，由此得

式中：C為常系數；w0為光束的束腰半徑；f為透鏡焦距。為了獲得式（1），推導過程中使用了德拜近似條件，即faλ和a2/（λf）1。

考慮R-S理論，使用振幅分布與式（2）相同的徑向偏振光為入射光時，聚焦后的電場分布可表示為[9]

式中：E0為常系數；γ=1/w20+ik/（2f）；q=ξ-ik/（2γ）；ξ=（z+f）2+ρ2。為了獲得解析表達式（3），推導過程中忽略了透鏡孔徑的影響，因此為了將兩種理論計算結果放在同一條件下比較，式（1）中的α取為π/2，即透鏡的數值孔徑取為1。考慮到透鏡的有效孔徑取決于入射光斑的實際尺寸，可以將透鏡的實際有效數值孔徑定義為

2 模擬結果及討論

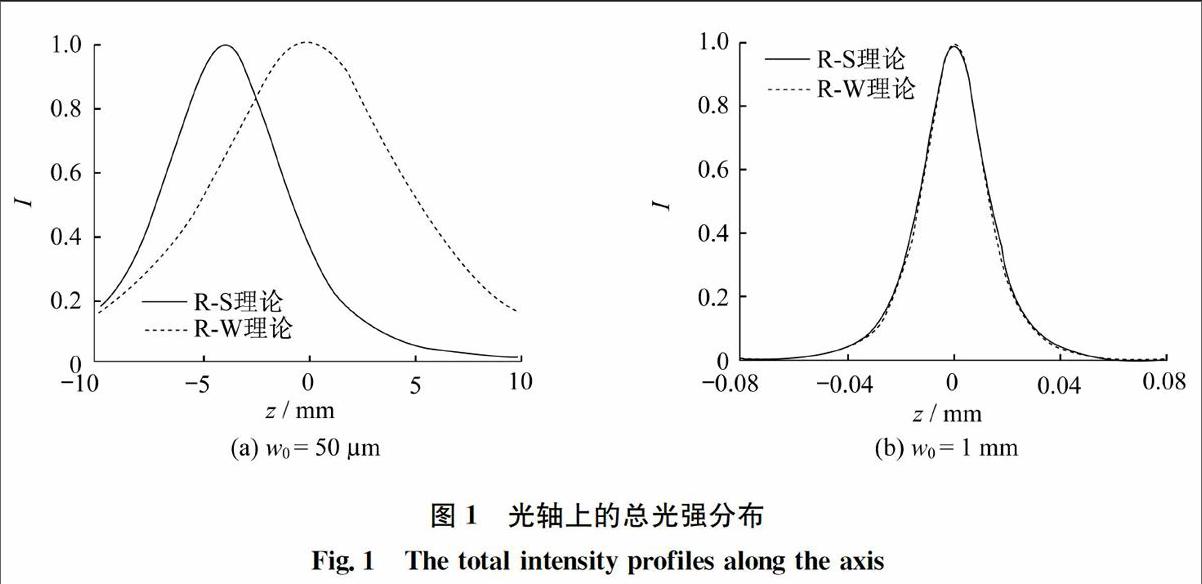
我們利用模擬軟件MATLAB進行計算模擬。先考慮小菲涅耳數系統，以氦氖激光為入射光源，波長λ=632.8 nm，入射光的束腰半徑w0=50 μm，透鏡焦距f=10 mm，此時菲涅耳數N≈0.4，有效數值孔徑NAeff=0.005。圖1（a）給出了使用兩種方法計算的光軸（z軸）上的總光強分布。從圖中可以看出：RS理論的計算結果出現了明顯的焦移現象，光強最強的位置向透鏡方向移動；而RW理論由于使用了德拜近似，光強最大值始終出現在幾何焦點位置（z=f），無法探討焦移現象。因此對于小菲涅耳數系統，由于不滿足德拜近似條件，RW理論不能給出正確的結果。其他計算參數保持不變，圖1（b）給出了w0=1 mm時的計算結果。此時菲涅耳數N≈158，有效數值孔徑NAeff=0.100。在這種情況下，菲涅耳數遠遠大于1，焦移現象消失，滿足德拜近似條件，RW理論可以給出正確的結果，此時兩種理論的計算結果吻合得很好。

接下來比較兩種理論在不同有效數值孔徑NAeff下的計算結果，以下的計算保持波長λ=632.8 nm和w0=1 mm不變。圖2（a），（b）和（c）分別給出了NAeff=0.2時，使用兩種理論計算的焦平面上沿x軸方向的總光強、徑向分量和縱向分量光強分布（I總=I徑向+I縱向），計算結果相對總光強的最大值做了歸一化處理。從圖中可以看出：由于偏振奇點的存在，徑向分量光強分布為中空的暗焦斑；在低有效數值孔徑的情況下，縱向分量光強所占總光強的比例遠小于徑向分量光強，因此總光強也呈現出中空的分布；在NAeff=0.2時，兩種理論的計算結果吻合得很好，這說明在數值孔徑較小的系統中，這兩種理論都適用。

圖3給出了NAeff=0.4時的計算結果，隨著有效數值孔徑的增大，聚焦光斑尺寸減小，縱向分量光強所占總光強的比例增加，此時兩種理論的計算結果開始出現明顯的差別。RS理論計算的聚焦光斑仍呈現出部分中空結構，而RW理論的計算結果顯示聚焦光斑已成為亮焦斑，中空結構消失。這是由于RW理論計算的縱向分量光強此時已占主導地位，而對于RS理論的計算結果來說，雖然縱向分量光強所占總光強的比例有所增加，但還不占主導地位，因此總光強仍出現了中空結構。由此可見，相對于RW理論，RS理論對縱向分量的地位估計不足。

圖4給出了NAeff=0.9時的計算結果，這時隨著有效數值孔徑的進一步增大，大部分光強集中到縱向分量上。比較兩種理論的計算結果，可以發現RS理論計算的徑向分量和縱向分量的光斑尺寸都明顯小于RW理論的計算結果，導致聚焦光斑整體尺寸較小。由于數值孔徑接近于1，RW理論計算的縱向分量出現了明顯的旁瓣，這是由衍射造成的，并很難消除，而RS理論計算的縱向分量其旁瓣幾乎可以忽略。

通過上述比較可以發現，這兩種理論在有效數值孔徑為0.4左右時就出現了明顯的差異，而且隨著有效數值孔徑的增大，差異越來越大。究其原因，這是由于RS理論雖然是離軸矢量理論，但在推導過程中使用了兩個近似[9]，一是使用了標量理論中傍軸近似條件下的理想薄透鏡的相位變換關系，二是使用了弱離軸近似關系

正是這兩個近似的使用使得RS理論對光波的衍射效應和矢量性估計不足，導致了縱向分量的比例偏低，聚焦光斑尺寸偏小且幾乎無旁瓣出現等現象。因此，RS理論雖然可以得到聚焦電場的各方向分量，符合矢量理論，但不能用于大數值孔徑的緊聚焦系統。但是這種方法還是要優于標量理論，因為其可以討論偏振態對聚焦光場的影響。

3 結 論

通過與RW矢量衍射理論的計算結果比較，本文發現RS理論雖然是矢量衍射理論，但只能適用于有效數值孔徑小于0.4的系統。這是由于這種理論在推導過程中使用了標量衍射的傍軸近似條件，使得其在數值孔徑較大的系統中對光波的衍射效應和矢量性估計不足，計算所得的聚焦光斑尺寸偏小。因此，在探討矢量光的低數值孔徑聚焦問題時，可以使用該方法，其可以獲得解析解，便于分析討論和計算，且能解釋焦移現象，但對于緊聚焦大數值孔徑系統，這種方法是不適用的。

參考文獻：

[1] RICHARDS B，WOLF E.Electromagnetic diffraction in optical systems.II.structure of the image field in an aplanatic system[J].Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1959，253（1274）：358379.

[2] WOLF E.Electromagnetic diffraction in optical systems.I.an integral representation of the image field[J].Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1959，253（1274）：349357.

[3] SHEPPARDC J R.Validity of the debye approximation[J].Optics Letters，2000，25（22）：16601662.

[4] KOTLYAR V V，KOVALEV A A.Nonparaxial propagation of a gaussian optical vortex with initial radial polarization[J].Journal of the Optical Society of America A，2010，27（3）：372380.

[5] LI YN，REN ZC，QIAN SX，et al.Analytical formulae of tightly focused laguerre-gaussian vector fields[J].Journal of Optics，2014，16（10）：105702.

[6] WANG H F，SHI L P，LUKYANCHUK B，et al.Creation of a needle of longitudinally polarized light in vacuum using binary optics[J].Nature Photonics，2008，2（8）：501505.

[7] HUANG K，SHI P，KANG X L，et al.Design of doe for generating a needle of a strong longitudinally polarized field[J].Optics Letters，2010，35（7）：965967.

[8] YOUNGWORTHK S，BROWNT G.Focusing of high numerical aperture cylindrical-vector beams[J].Optics Express，2000，7（2）：7787.

[9] GU B，CUI Y P.Nonparaxial and paraxial focusing of azimuthal-variant vector beams[J].Optics Express，2012，20（16）：1768417694.