三自由度直升機多模型LQR控制器設計

摘要 通過對三自由度直升機模型實驗系統的總體分析，引入了多模型切換思想，建立了多模型LQR控制器。針對多模型LQR控制器將數學模型以高度角和俯仰角兩個角度為變量建立多模型集合，運用Matlab搭建仿真對控制器進行仿真實驗，并通過直升機高度角、俯仰角和旋轉角的跟蹤準確性、快速性以及超調量大小等控制指標，直接地度量控制器控制效果的好壞，將控制效果最優的多模型LQR控制器應用于直升機實物模型之上，運用Matlab中的實時工作空間（RTW）和Quanser公司專用控制軟件Wincon實現對直升機實物的實時控制，控制效果良好。

關鍵詞 三自由度直升機模型；LQR控制器；多模型LQR控制器

中圖分類號 TP2 文獻標識碼 A

Summary：In this paper， the multi-model set of 3-DOF is built， based on model switch idea and the LQR controller is established by analyzing the whole helicopter system. The multi-model set is achieved and differed by high angle and pitch angle and the controller is designed and simulated in Matlab. With the real-time value of control variables， the performance of the designed controller is shown. The real controller is built in Matlab RTW with the help of Wincon software interface of Quanser. The results of the simulation is shown the effectiveness of the designed system.

Key Words：3-DOF helicopter model； LQR controller； multi-model LQR controller

引言

二十世紀七十年代末我們開始了對直升機的研究，分別從美法等直升機研究水平處于世界領先地位的發達國家引進了諸如“Black Eagle”和“Apache”等成熟的直升機機型。但是長久以來我們的努力只是停留如何去模仿別人，最多達到在別人的基礎上稍作修改，并沒有真正在直升機的技術核心領域獲得成功，比如直升機飛行最為核心的操控系統，就鮮有成績，這就給后來學者和研究人員提出了更高的要求，促使我們進一步探索[1]。

在國內高校方面，研究本課題的有：東北大學的劉鑫，首先針對直升機設計PID控制器，然后設計直升機系統的模糊控制器，最后將兩者合二為一，設計出模糊控制和PID控制相結合的控制方法，取得良好效果；山東大學的葛金來，他不但設計了PID和LQR控制器，還對直升機模型有無動態干擾模塊（Active Disturbance System， ADS）擾動進行了實驗，最后還對直升機模型進行了基于保性能的控制研究[13]；國外的，如Jonas Witt利用非線性近似模型預測控制設計控制器；Ali T. Kutay完成了通過自適應輸出的反饋控制；Konstantin K. Starkov則針對非線性系統設計了一種滑模控制器來實現控制；Mitsuaki Ishitobi也在前人基礎上利用參數辨識的方法進行了一系列閉環控制。以上控制方法都沒有對直升機模型系統進行建模，而是利用非線性系統的理論分析方法來設計控制器。但是，非線性理論本身就不是一套完善的理論，所以在設計控制器時不可避免的存在一些近似或者忽略次要影響因素，導致真正的實時控制在精度上并不那么讓人滿意，絕大多數仍只是停留在仿真的階段，但是對要求不是十分苛刻的系統仍然具有較大的參考指導價值。

本文主要以加拿大Quanser公司研發制造的三自由度直升機模型為實驗平臺，基于系統自帶的Matlab-RTW（Real-Time Workshop， RTW）實物仿真控制系統，在此開發環境下對雙旋翼三自由度直升機模型進行深入理論研究，并運用理論成果設計新型控制器達到控制直升機模型位置和飛行速度的目的。

1三自由度直升機模型實驗系統的結構組成

本實驗系統作為研究縱列式雙旋翼直升機的仿真平臺，在結構上主要由硬件系統和軟件系統兩部分組成。其中，硬件系統又包含機械控制系統和電氣控制系統兩部分。控制過程可簡單描述如下，直升機飛行姿態通過數據采集卡傳遞給計算機，計算機對各變量進行實時處理，然后將控制指令通過運動控制卡傳遞給電源模塊來控制直升機驅動電機的供電電壓，以此來調整模型的飛行姿態。整個實驗系統可以用如圖1所示的框圖來清晰地表示出來。

1.1直升機模型硬件系統

本文所使用的Quanser公司三自由度直升機模型實驗系統的硬件系統由直升機本體、電源模塊、數據傳輸線、數據采集卡和一臺計算機組成。其中，直升機本體屬于硬件系統中的機械控制部分，數據傳輸線、數據采集卡、電源模塊和計算機屬于硬件的電氣控制部分。

1.2直升機模型軟件系統

本文直升機模型實驗系統采用的軟件系統完全安裝在一臺實驗專用計算機中，包括由Quanser公司自行開發的基于Matlab中Simulink軟件包和TCP/IP技術的控制軟件Wincon[2]和從Simulink生成優化而來的RTW實時工作空間。

2基于多模型切換的LQR控制器設計

2.1 多模型控制方法的基本原理

多模型控制主要由以下三部分組成：

2.2多模型控制器的構成

在運用多模型控制理論建立控制器的過程中，大致只有兩個步驟，那就是針對模型集中的每個單一模型建立最為適合的控制器，然后運用諸如模型切換或加權平均的方法將這些控制器集中起來，完成最終控制器的設計，下面就對多模型控制器設計中最常用的兩種方法簡單討論：

1） 通過加權建立多模型控制器[3，4]：方法需要運用到數學理論中的分割定理，根據每個獨立模型的權重比例，運用概率加權的方法，得出最終的控制器。

2） 根據某種切換策略建立多模型控制器：保證控制器切換時的穩定性是此種方法的首要前提，由于該方法相對第一種方法較為直接，設計難度也不大，所以各類研究成果層出不窮[5，6]。

本文的研究過程中，運用到的就是上文介紹的第二種多模型研究方法，即模型切換的控制策略。

2.3三自由度直升機多模型LQR控制器設計

圍繞研究對象三自由度直升機模型實驗系統，根據模型的實際變化特性來建立多個模型，組成一個合理的多模型集合，盡量逼近直升機系統在飛行過程中的真實動態性能，再基于此多模型集合設計出多模型控制器集合，最后根據真實飛行狀態的不同選取最逼近當前狀態的模型，用其對應的也就是最適合當前直升機狀態的控制器來實施控制策略，從而實現對復雜系統進行更有效控制的目的。

由此，結合直升機模型飛行過程中的實際情況，采用模型切換的思想，而不是模型加權理論，根據直升機飛行過程中的具體位置，建立適合當前系統的模型參數，同時設計多組LQR控制器，每組控制器都分別設定符合當前情況的 和 矩陣取值，得到最直接最有效的控制量，使得直升機跟蹤給定信號既快速又準確。控制方法結構框圖如圖2所示。

2.3.1 多模型集合的建立

在多模型控制理論的實現過程中，首當其沖的難題就在于如何針對控制過程建立清晰明確的數學模型，在實際研究過程中，只能把系統的輸入輸出作為切入點，采用一些常見的辨識方法，例如非線性自回歸滑動平均模型等。先分解再合成的多模型控制策略就可以對這個問題有一定程度的解決，有些結構復雜的對象系統，無法得出能夠包含整個控制域的模型，所以采用分段方法，對每個分段區域建立恰當的模型，然后將這些分段模型進行數學處理，無論是加權還是切換，都是可行的手段。這種方法主要包括兩個大的方面：一是將問題進行分解；二是運用恰當方法進行合成。詳細步驟可以按以下操作：

1） 引入一種恰當的規則，對整個控制域進行分解，分成符合要求并且結構較為簡單的幾個部分；

2） 針對每個部分建立數學模型和控制器；

3） 終極目標則是選取一種合適的方法，將之前分解的分段模型和控制器進行有效組合，得出最終結果。

通過查閱大量相關文獻，了解到在多模型方法建立模型集合的領域內，非線性系統的線性化[7]、T-S型模糊多模型[8-10]、神經元網絡多模型[11]、即時學習算法[12-16]等手段應用較為廣泛，效果也很明顯。

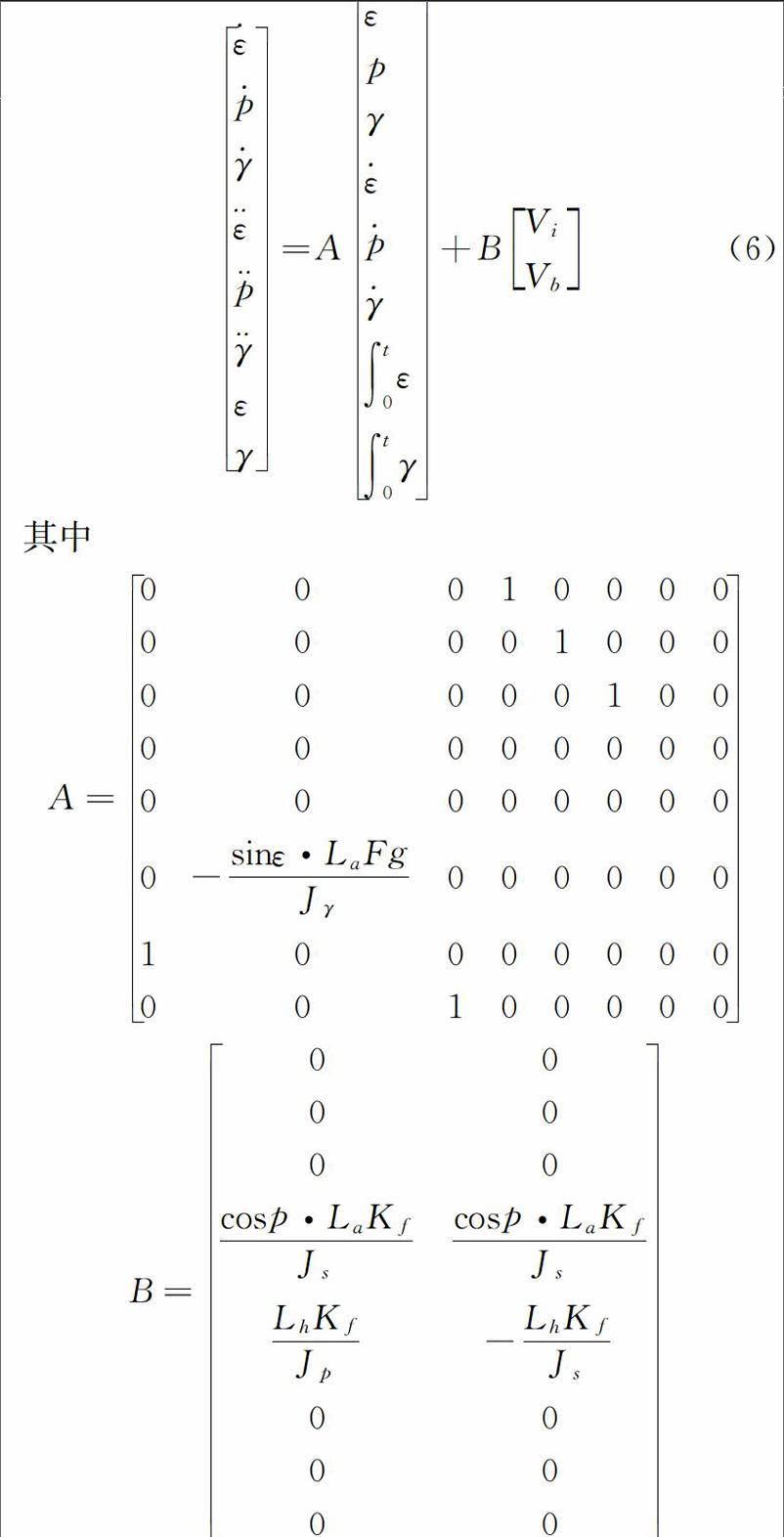
針對Quanser公司三自由度直升機模型實驗系統的結構特點，再在原有數學建模的基礎上，加深對實驗系統物理特性的分析，將之前的近似和線性化重新考慮起來，建立其更為準確的數學模型。將直升機的高度角 和俯仰角 作為多模型集合建立的切入點，得出多模型LQR控制器的多模型集合，如表1所示。

3.1直升機模型實時控制

整個實物仿真過程的實現大致可以分成以下三個部分：

1） 控制算法的編寫和控制器的搭建，這一步的完成與我們之前的仿真控制器設計是類似的，都是利用了Matlab中的.m文件和Simulink工具包，使得研究人員可以方便直觀地調用Matlab中強大的模塊庫來簡化整個設計過程；

2） 在將控制算法的編寫和控制器的設計完成之后，可以直接通過Matlab-RTW實時工作空間自動完成從便于研究人員設計的模塊化程序化的框圖語言向便于機器識別和運行的語言的編譯轉化過程；

3） 最后，通過Quanser公司自己研發的基于Matlab中Simulink軟件包和TCP/IP技術的控制軟件Wincon，將編譯好的控制語句作用在通過編碼器和數據傳輸線連接在數據采集卡和電源模塊上的三自由度直升機機體上，實現控制直升機模型實物的最終目的。

3.2 LQR控制器和多模型LQR控制器仿真及實物控制效果對比

單一模型LQR控制器和多模型LQR控制器在Simulink仿真以及后續實物平臺的控制效果進行對比和分析。

首先在Matlab中用單一模型LQR控制器對直升機模型進行仿真實驗，在仿真的初步階段，采用較為簡單的函數曲線作為給定信號。

將一個周期為100秒幅值為20的正弦信號作為高度軸的給定信號，單一模型的LQR控制器跟蹤效果如下圖3所示。

同樣的，將相同的周期100秒幅值20的正弦信號作為給定信號，用所設計的多模型LQR控制器來進行高度軸的飛行跟蹤控制，結果如圖4所示。

通過上面的圖3和圖4的對比，可以非常清晰地發現，單一模型LQR控制器在跟蹤正弦函數曲線的過程中超調量較大，調節時間較長，在兩個周期也就是仿真時間到達200秒的時候才能達到較好的跟蹤效果，而多模型LQR控制器的表現就大大優于單一模型LQR控制器了，不僅在50秒左右就能夠很好地跟蹤上給定信號的變化，而且在調節的過程中超調的幅度也是遠小于單一模型LQR控制器的。

在完成對兩個控制器的初步仿真實驗之后，接下來就要進行更加復雜的實驗，將給定的函數信號變為階梯方波便是最有效最合理的方式。因為階梯方波是一組不停變化的信號，這樣就對直升機在飛行時不斷變換飛行姿態時的實際需求進行了很好的模擬。同時，階梯方波又可以在一段時間內保持平穩，恰好又符合飛機飛行過程中有大段時間平穩飛行的實際。所以，階梯方波是能夠完美模擬直升機真實飛行狀況的良好跟蹤信號源。

在實物仿真中，采用對直升機實際飛行最具有仿真性和現實意義的階梯方波作為給定信號，高度軸和旋轉軸的跟蹤效果分別如圖5和6所示。

從實物曲線可以看出，多模型LQR控制器運用在直升機實物上表現依舊讓人滿意，說明我們設計的控制器是相當成功的。

4結束語

本文首先介紹了Quanser公司三自由度直升機模型實驗平臺的結構組成，并對硬件系統和軟件系統分別進行了介紹。通過對于多模型控制的研究，將多模型LQR控制器的設計重點放在了通過模型切換思想實現多模型控制上。之后針對多模型控制建立多模型集合的需求，對之前直升機模型的數學建模進行了優化，在微分方程中恢復了之前被近似化忽略掉的角度影響因素，并針對高度角和旋轉角兩個角度變量設計多模型集合，同時對應每個模型設計LQR控制器，得到一個LQR控制器集合，完成多模型LQR控制器的設計。通過實際仿真的效果對比，多模型控制器的優勢得到很大發揮，控制效果明顯優于單一模型的LQR控制器。而在隨后的直升機實物控制中，多模型LQR控制器的表現仍然很好。

參考文獻

[1] 劉廣磊，申濤. 三自由度直升機多模型LQR控制方法[J]. 濟南大學學報（自然科學版），2014，28（1）：45-49.

[2] 吳森堂，費玉華. 飛行控制系統[M]. 北京：北京航空航天大學出版社，2010：105-136.

[3] 周煥銀，劉開周，封錫盛. 基于權值范圍設置的多模型穩定切換控制研究[J]. 控制與決策，2012，27（3）：349-354.

[4] Erin M. Aylward， Pablo A. Parrilo， Jean-Jacques E. Slotine. Stability and robustness analysis of nonlinear systems via contraction metrics and SOS programming[J]. Automatica，2014，44： 2163–2170.

[5] Mitsuaki Ishitobi， Masatoshi Nishi . Nonlinear Model following control with parameter identification for a 3dof model helicopter[J]. Advanced intelligent mechatronics，2009，32：253-267.

[6] Zhivoglyadov PV， Richard HM， Fu MY. Further results on localization-based switching adaptive control[J]. Automatica，2011，37：257-263.

[7] 馬娟麗. LQR系統最優控制器設計的MATLAB實現及應用[J]. 石河子大學學報（自然科學版），2013，23（4）：519-521.

[8] Patton R J. Synchronization of decentralized multiple-model systems by market-based optimization[J]. IEEE Trans. Systems， Man and Cybernetics， Part B， 2004， 34（1）： 665-671.

[9] Patton R J， Lopez Toribio C J， Simani S. Robust fault diagnosis in a chemical process using multiple-model approach[C]. Proceedings of the 40th IEEE Conference on Decision and Control. Orlando Florida USA， Expert Systems with Applications .2010： 349-354.

[10] Yang Haiqing， Yu Li， Xu Chi. Multiple model adaptive control of automatic quasi-synchronization for 500 kW hydropower generator[C]. Intelligent Control and Automation， 2004. WCICA. Fifth World Congress on， Hangzhou， P.R. China， Automation in Construction . 2004：5112-5115.

[11] Jonas Witt， Sudchai Boonto. Approximate model predictive control of a 3dof helicopter[C]. Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans， SPIE .2007：1243-1251.

[12] Konstantin K. Starkov， Luis T. Sliding Mode control synthesis of a 3dof helicopter prototype using position feedback[J]. Variable Structure Systems， 2008， 8：233-237.

[13] Bontempi G， Birattari M， Bersini H. Lazy learning for local modelling and control design[J]. Int. J Control， 2009， 72 （7/8）： 643-658.

[14] Zheng Q B， Kimura H. Just-in-time modeling for function prediction and its applications[C]. Proceedings of the 3rd Asian Control Conference， Shanghai， China， Fluid Dynamics Research .2008：1816-1821.

[15] 尹秀云，李擎. 基于LQR最優控制系統的設計[J]. 微計算機信息.2012，23（1）：55-57.

[16] 孫維，王偉，朱瑞軍. 即時學習算法在非線性系統迭代學習控制中的應用[J]. 控制與決策，2003， 18（3）：263-266.

聯系方式

聯系作者：孫莉

地址：濟南市歷城區七里河小區35號樓4單元601

郵編：250100

E-mail： sunli2005sd@163.com

手機：13583113227

備注：開發票

發票抬頭：山東協和學院