基于主元相似度的間歇過程操作曲線遞推優化

仇力，欒小麗，劉飛

（江南大學輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122）

基于主元相似度的間歇過程操作曲線遞推優化

仇力，欒小麗，劉飛

（江南大學輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122）

針對一類較長周期的間歇過程操作優化問題，提出了一種基于正常運行批次的數據驅動型操作曲線遞推優化方法。首先采用分段離散化方法將原非線性優化問題轉化為線性優化問題，再利用主元分析對離散化后的高維時段變量進行降維處理，然后在降維后的主元平面中，基于時段變量與最終產品指標間的余弦相似度，實現對原操作曲線的攝動優化。考慮到時段變量方差和相似度隨批次會發生變化，建立了遞推算法以實現操作曲線的遞推更新。最后將該方法應用于某化工產品的間歇結晶過程中，結果驗證了所提方法的有效性。

間歇過程；操作軌跡優化；主元分析；余弦相似度；遞推算法

引 言

隨著現代社會對多品種、多規格和高質量產品需求的提高，以小批量、精細化和高附加值為主要特征的間歇生產過程得到快速發展。相比于連續過程，間歇過程沒有穩定的靜態工作點，過程操作的基本方式是確保批次過程跟蹤設定操作曲線[1-2]。間歇過程的優化目標通常為縮短運行周期或提高終端產品產量和質量[3]。在完成有效的動態控制基礎上，間歇過程操作曲線的優化成為提高經濟效益的關鍵。

間歇過程的操作優化概括分為機理驅動型優化和數據驅動型優化[4]。機理驅動型優化需要過程精確的機理模型，要求對過程有深入的理解[5-9]，而間歇過程是復雜的動態非線性過程，其建模相當困難，這限制了機理驅動型優化的發展。數據驅動型優化分為基于經驗模型的優化，實驗設計以及無模型優化。常用的經驗模型有人工神經網絡[10-12]、偏最小二乘[13-16]、支持向量機[17-19]等。由于經驗模型精度受限于樣本數，一般而言模型外推性差；實驗設計[20-23]通過有目的的試驗獲得過程響應與輸入間的數值關系，但基于實驗設計的優化基于實際運行裝置進行，成本高且效率低。結合基于模型優化的高效性和實驗設計的可行性，Kong等[24-26]提出了無模型優化方法。無模型優化通過一系列迭代點的在線試驗來實現，它避免了模型失配，提高了優化效率，該方法在注塑成型過程中取得成功的應用。無模型優化方法適用于快速、低成本的間歇過程，它要求過程單批次成本低，用于優化的少數試驗批次在經濟上可以接受。對于較長工作周期的間歇過程，該方法的實施成本將會顯著提高。

針對上述問題，提出一種基于時段變量相關性分析的數據驅動型操作曲線優化方法。基于分段離散化方法將原非線性優化問題簡化為線性優化問題，在降維的基礎上，利用離散化后的各時段變量對指標變量的作用強弱和方向，通過遞推修正算法實現對操作軌線的遞推更新。該方法突破了文獻[24-26]中無模型優化方法對于間歇過程操作周期快速，批次實驗成本要低等假定和要求。優化算法完全基于正常生產運行數據而不是迭代點的在線試驗，實施成本低，能解決長周期、實驗成本高的間歇過程操作優化問題。最后該方法被成功用于某化工產品的間歇結晶過程溫度操作曲線優化中。

1 問題描述

間歇過程操作優化的目的是在一個批次過程結束時，產品的產量或質量得到提高、過程操作的周期能夠縮短。在間歇過程直接控制層已經實現對給定曲線的動態跟蹤基礎上，優化層的目標是如何確定最優的操作曲線，其數學描述如下：

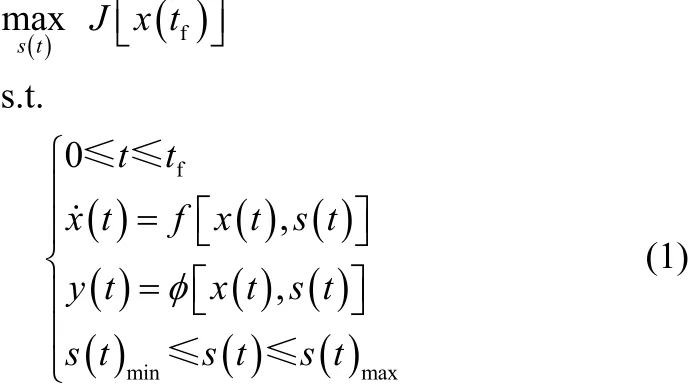
其中tf為間歇過程周期，J是性能指標，s(t)為設定操作曲線，x(t)是狀態變量, 即按設定操作曲線控制時，被控過程可測量狀態的當前測量值，y(t)是輸出變量，s(t)min和s(t)max分別是操作曲線的下界和上界。上式意義為在滿足約束的條件下尋找一條合適的操作曲線，使得間歇過程結束時性能指標最優或次優。以下討論中，性能指標的終值J[x(tf)]，稱之為批次的指標變量。

2 優化策略及算法

2.1 分段離散化和時段變量的構造

間歇過程的操作優化本質上是一個非線性優化問題。一方面為了將原非線性優化問題轉化為線性優化問題，可采用分段離散化方法將非線性過程區間劃分為多個線性子區間；另一方面考慮到控制系統設計實施的可行性，最優操作軌線往往是以分段方式進行[24]。因此首先采用分段離散化方法[27-28]將原操作曲線以及狀態變量曲線用m-1個分段點等時間間隔分成了m段（圖1），即：

其中sl為離散化后的操作曲線設定值，xl為離散化后的狀態變量，記為時段變量。由此非線性優化問題（1）轉化為離散化形式如下：

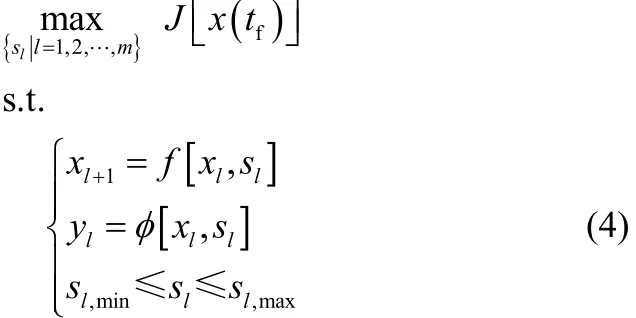
其中 sl,min和 sl,max分別是操作曲線離散化后的下界和上界，yl是離散化后的輸出變量。優化的目標為找出合適的操作曲線設定值集合{sl|l=1, 2,…, m}使性能指標最優。

圖1 分段離散化Fig.1 Discretization with segmentation

n個批次的時段變量構成了 n×m維矩陣 X，X=[x1, x2,…, xm]；相應的n個批次指標變量，構成n×1維矩陣Q，并令Z=[X Q]。為敘述方便，下文所用矩陣均為標準化后的矩陣。

注：當m趨向于無窮大時，分段后的軌線可以以任意精度逼近原動態曲線。為保證離散化后優化命題與原優化命題的等價性，m應該取一個較大的值。m取值的大小，一般要根據整個過程的周期和動態特性快慢，既要滿足對動態系統的采樣頻率要求（即滿足香濃采樣定理），也要考慮到不使數據維數過高。

2.2 基于時段變量降維和重構的優化策略

考慮到Z為高維矩陣，為了用較少的變量更直觀地反映間歇過程各時段操作條件對指標變量的影響，可使用主元分析對其進行降維處理，因此將Z∈Rn×(m+1)可分解為m+1個向量外積和：

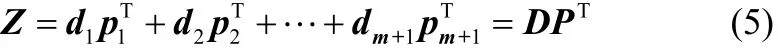
其中di∈Rn(i=1, 2,…,m+1)為得分向量（主元變量），pi∈Rm+1為載荷向量，Dn×(m+1)為得分矩陣，P(m+1)×(m+1)為載荷矩陣，PT為 P的轉置矩陣。各得分向量之間相互正交，各載荷向量之間也為正交關系，且每個載荷向量均為單位長度。

為了將優化控制量施加到具體過程操作中，必須將原時段變量表示成主元變量的線性組合，即對主元分解后的數據進行重構。考慮由前 r(r≤m+1)個主元張成的r維平面，做原變量zi關于d1, d2,…,dr的線性回歸，即求回歸方程：

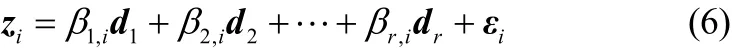
其中εi是回歸誤差，Z=[z1, z2,…, zm+1]，記回歸系數 βi=[β1,i, β2,i,… , βr,i]T，記 d=[d1, d2,…, dr]，則：

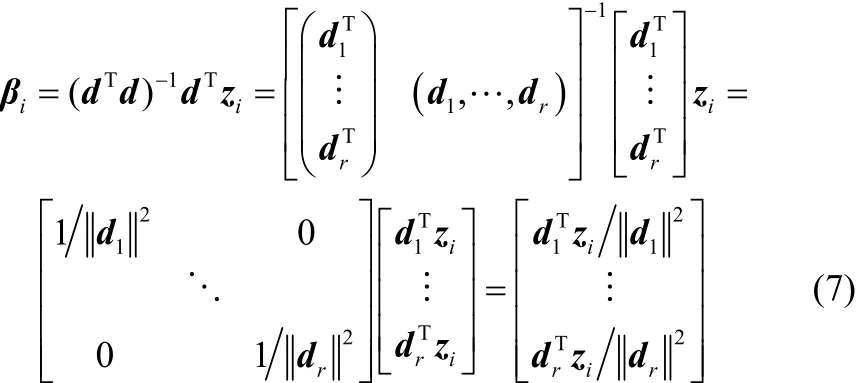
所以：

通常根據累計方差貢獻率確定主元的個數。一方面由于操作曲線離散化后各時段變量間時序相關性較大，因而前兩個主元可以包含過程數據大部分信息；另一方面二維平面可以更直觀地得出各時段變量對指標變量的懾動量大小和方向，因此考慮主元個數r=2時的特殊情形，此時式（9）簡化為：

圖2為前兩個主元d1和d2構成的二維載荷平面，x?l是重構后的時段變量，?Q是重構后的指標變量，θl是重構后時段變量與指標變量間的夾角，它直觀地表達了各時段變量對指標變量的拉動力量強弱關系。換言之，夾角越小，則相關性或貢獻強度越大。物理意義是該時段的控制對最終指標變量有更顯著的影響。為此在每個時段上，依據時段變量對指標變量的作用強弱和方向，對原操作曲線進行攝動，即：

上面的方法意味著，攝動后的操作曲線是在原曲線的基礎上加上矯正量，使得每個時段都對指標變量產生正的貢獻。特別指出的是，每一時段的最大攝動量沒有超過各批的一個標準差，從而依然滿足原來優化問題（4）的約束條件。

2.3 遞推算法

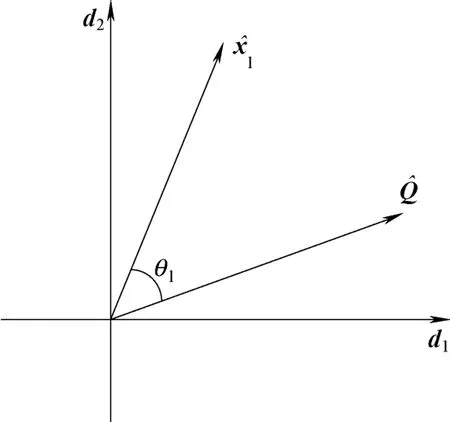
圖2 前兩個主元載荷圖Fig.2 Loading plot with first two principal components

間歇過程時段變量與指標變量間的關系隨著批次的變化而變化，因而需要用新批次數據修正變量間的相關關系。基于遞推PCA算法[29-30]導出操作曲線的滾動修正算法。

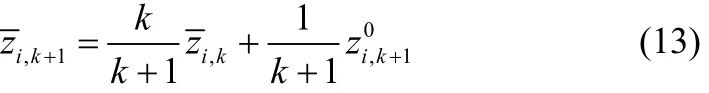
其方差的遞推式為：

其中 σi,k是離散化后前 k批次數據的標準差，

前k批次數據矩陣Zk×(m+1)的自相關矩陣Rk的遞推式為：

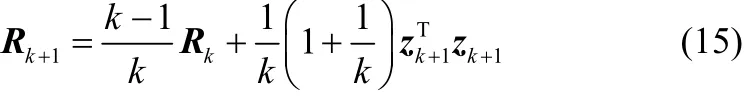
因為Rk為實對稱矩陣，可對其進行正交分解，即為更新前主元的載荷矩陣，Λk對角矩陣，為P的轉置矩陣，則自相關矩陣可k化簡為：

對實對稱矩陣(E+εuu)T進行正交分解：

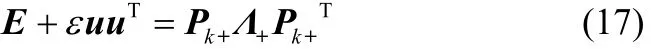
其中Pk+為新的正交矩陣，Λ+為新的對角矩陣，為Pk+的轉置矩陣，則：

由式（18）知，載荷矩陣的遞推式為：

由式（12）結合式（19）中遞推后的載荷矩陣的前兩列可求出遞推后時段變量與指標變量間的余弦，并進一步得出操作曲線的更新方法。

對操作曲線的攝動優化式（11）兩邊求差分得：

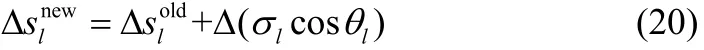
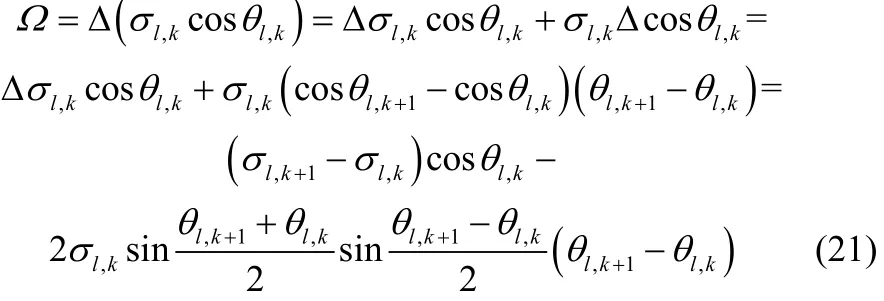
其中 θl,k是前 k批數據重構后時段變量與指標變量間的夾角，式（21）中后一項的變化相對于前一項可忽略不計，則操作曲線的遞推式可表示為：

上述遞推優化方案的意義是，在上一批次操作曲線優化結束后，利用下一批次采集的新數據，對上一批次的優化結果做修正處理，以形成下一個批次新的操作曲線，從而實現操作曲線的滾動優化。為便于理解，圖3給出如下間歇過程優化算法流程圖。

圖3 優化算法流程Fig.3 Flow chart of optimization algorithm

3 實例研究

以某化工產品間歇結晶過程為研究對象，其原理如圖4所示。在預結晶階段，保持設定溫度為定值，讓進料從結晶罐上方流入結晶器，然后降低設定溫度，使得目標產品和部分雜質從進料溶液中以晶體的形式析出附著在結晶器換熱管的外表面，升高溫度使得雜質以液態形式流進儲料罐并排出，最后再次升高溫度使得目標產品達到熔融溫度，以液態的形式流入儲料罐。由結晶的原理知：當設定溫度不同時，最終得到的目標產品濃度也不同。

圖4 間歇結晶過程原理Fig.4 Schematic diagram of batch crystallization processes

間歇結晶過程是一種多維的動態非線性過程，其操作周期為120 min左右。為了確保分段后的軌線盡可能逼近原來的操作曲線，同時分段不至于太密集導致時段變量維數過高，文中取1 min為時段間隔，時段變量的取值為每1 min內溫度的平均值，指標變量為結晶后的產品濃度。采集結晶過程正常運行時81批的數據，選擇其中最短的長度（m=107）作為標準，其余批次采用截尾的方法與最短長度對齊。初始優化曲線可以使用原設定操作曲線，或用一定量的歷史操作數據，用離線方法進行先期優化，從而得到一個更好的優化初始曲線。事實上先期離線優化計算方式，可以大大加快優化速度，使得操作曲線在很少的批次后，達到對過程的優化和跟蹤。為說明本方法的算法步驟，文中用70批數據離線計算以獲取遞推優化的初始值，剩余的11批數據作為實時操作數據用作操作曲線的遞推更新。

對前 70批數據 X70×107進行標準化處理，對處理后的矩陣X主元分解，并采用前兩個主元重構原時段變量，得出各時段的溫度對最終目標產品濃度的作用關系后，利用剩余的11批數據基于式（19）對時段變量與指標變量間的相關關系進行遞推更新，最終得出遞推更新后各時段的溫度對最終目標產品濃度的作用關系。

然后，再分別利用式（11）與式（23）對溫度操作曲線進行更新，結果如圖5所示。圖中實線為優化前操作曲線，點虛線為由81批數據攝動優化得到的操作曲線，虛線為采用81批數據遞推優化得到的操作曲線。

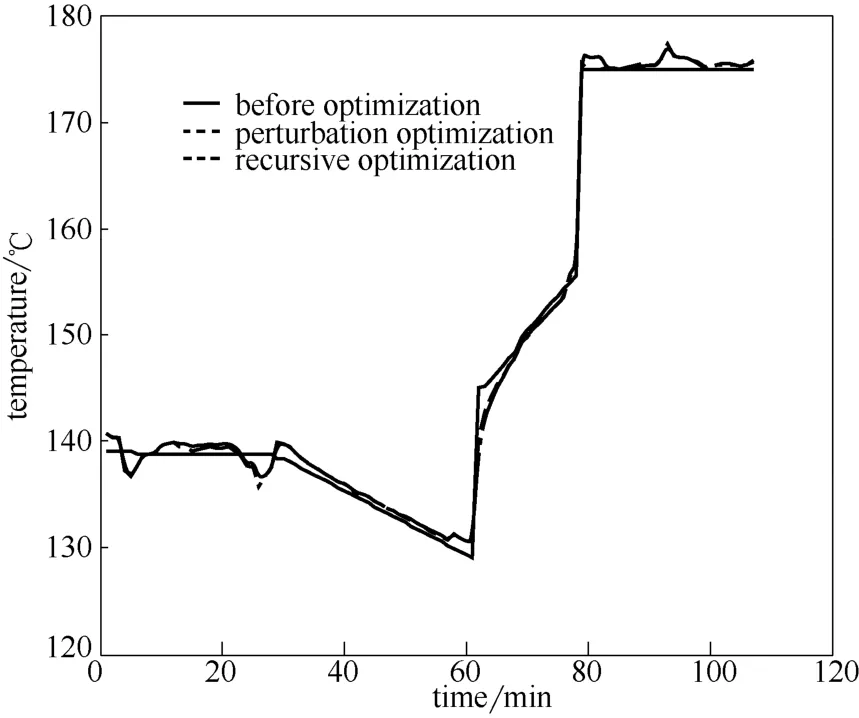
圖5 優化前后操作軌線比較Fig.5 Trajectory before and after optimization

為驗證優化后操作曲線的有效性，需建立目標產品濃度Q關于分段后溫度X的偏最小二乘預測模型：

其中ω為回歸系數矩陣。

由預測模型可以算出，優化前的操作曲線對應的產品濃度為97.46%，采用81批數據攝動優化后對應的預測濃度為97.58%，采用81批數據遞推優化對應的預測濃度為97.68%。優化前所有批次的產品濃度標準差為0.361%，本遞推算法可使產品濃度均值提高0.22%，即0.61個標準差。經過顯著性檢驗，此均值提高是顯著性的。實際效益方面，批次產品平均濃度的提高，相當于在相同濃度規格下提高了生產裝置產能約0.2個百分點（產品按有效濃度定價）。同時操作曲線的滾動遞推更新，能夠充分利用新批次操作帶來的信息，降低計算量，減少存儲空間，同時滿足原有操作約束條件。

4 結 論

針對一類較長周期的間歇過程操作優化問題，提出了一種數據驅動型操作曲線遞推優化方法。基于分段離散化將原非線性問題簡化，在主元降維后的平面中，結合各時段變量與指標變量間的余弦相似度和標準差對原操作曲線進行攝動。針對間歇過程中變量相關性隨批次而變化的特性，建立了操作曲線遞推算法，實現了操作曲線的滾動更新。將該方法應用到某化工產品間歇結晶過程中，產品預測濃度的提升驗證了該方法的有效性。

[1] 史洪巖, 苑明哲, 王天然. 間歇過程動態優化方法綜述 [J]. 信息與控制, 2012, 41 (1)： 75-82.SHI H Y, YUAN M Z, WANG T R. A survey on dynamic optimization methods of batch process [J]. Information and Control,2012, 41 (1)： 75-82.

[2] BONVIN D, SRINIVASAN B, HUNKELER D. Control and optimization of batch processes： improvement of process operation in the production of specialty chemicals [J]. IEEE Control Systems Magazine, 2006, 26 (6)： 34-45.

[3] 陳治綱, 許超, 邵惠鶴. 間歇過程優化與先進控制綜述 [J]. 化工自動化及儀表, 2003, 30 (3)： 1-6.CHEN Z G, XU C, SHAO H H. Batch process optimization and advanced control — a survey [J]. Control and Instruments in Chemical Industry, 2003, 30 (3)： 1-6.

[4] CHRISTOS G. Design of dynamic experiments： a data-driven methodology for the optimization of time-varying processes [J].Industrial and Engineering Chemistry Research, 2013, 52 (35)：12369-12382.

[5] DAI W, WORD P D, HAHN J. Modeling and dynamic optimization of fuel-grade ethanol fermentation using fed-batch process [J].Control Engineering Practice, 2014, 22 (1)： 231-241.

[6] ROSSI F, COPELLI S, COLOMBO A. Online model-based optimization and control for the combined optimal operation and runaway prediction and prevention in (fed-) batch systems [J].Chemical Engineering Science, 2015, 138： 760-771.

[7] 楊國軍, 李秀喜, 陳赟, 等. 間歇過程實時優化 [J]. 化工學報,2011, 62 (10)： 2839-2844.YANG G J, LI X X, CHEN Y, et al. Real-time optimization for batch process [J]. CIESC Journal, 2011, 62 (10)： 2839-2844.

[8] WANG J L, XUE Y Y, YU T, et al. Run-to-run optimization for fed-batch fermentation process with swarm energy conservation particle swarm optimization algorithm [J]. Chinese Journal of Chemical Engineering, 2010, 18 (5)： 787-794.

[9] YANG G J, LI X X, QIAN Y. A real-time updated model predictive control strategy for batch processes based on state estimation [J].Chinese Journal of Chemical Engineering, 2014, 22 (3)： 318-329.

[10] SINGHA B, BAR N, DAS S K. The use of artificial neural network(ANN) for modeling of Pb (Ⅱ) adsorption in batch process [J].Journal of Molecular Liquids, 2015, 211： 228-232.

[11] CHEN F D, LI H, XU Z H. User-friendly optimization approach of fed-batch fermentation conditions for the production of iturin A using artificial neural networks and support vector machine [J]. Electronic Journal of Biotechnology, 2015, 23 (4)： 273-280.

[12] 賈立, 施繼平, 邱銘森, 等. 基于無約束迭代學習的間歇生產過程優化控制 [J]. 化工學報, 2010, 61 (8)： 1889-1893.JIA L, SHI J P, CHIU M S, et al. Nonrestraint-iterative learning-based optimal control for batch processes [J]. CIESC Journal, 2010, 61 (8)：1889-1893.

[13] ZHANG Y W, FAN Y P, ZHANG P C. Combining kernel partial least-squares modeling and iterative learning control for the batch-to-batch optimization of constrained nonlinear processes [J]. Industrial and Engineering Chemistry Research, 2010, 49 (16)： 7470-7477.

[14] GE Z Q, SONG Z H, ZHAO L P. Two-level PLS model for quality prediction of multiphase batch processes [J]. Chemometrics and Intelligent Laboratory Systems, 2014, 130 (2)： 29-36.

[15] 賈潤達, 毛志忠, 王福利. 基于KPLS模型的間歇過程產品質量控制 [J]. 化工學報, 2013, 64 (4)： 1332-1339.JIA R D, MAO Z Z, WANG F L. KPLS model based product quality control for batch processes [J]. CIESC Journal, 2013, 64 (4)：1332-1339.

[16] ZHAO L P, ZHAO C H, GAO F R. Phase transition analysis based quality prediction for multi-phase batch processes [J]. Chinese Journal of Chemical Engineering, 2012, 20 (6)： 1191-1197.

[17] JIN H P, CHEN X G, YANG J W. Multi-model adaptive soft sensor modeling method using local learning and online support vector regression for nonlinear time-variant batch processes [J]. Chemical Engineering Science, 2015, 131： 282-303.

[18] ZHANG S N, WANG F L, HE D K, et al. Real-time product quality control for batch processes based on stacked least squares support vector regression models [J]. Computers and Chemical Engineering,2012, 36 (1)： 217-226.

[19] 劉毅, 王海清, 李平. 局部最小二乘支持向量機回歸在線建模方法及其在間歇過程的應用 [J]. 化工學報, 2007, 58 (11)： 2846-2851.LIU Y, WANG H Q, LI P. Local least squares support vector regression with application to online modeling for batch processes [J].Journal of Chemical Industry and Engineering (China), 2007, 58 (11)：2846-2851.

[20] FIORDALIS A, CHRISTOS G. Data-driven, using design of dynamic experiments, versus model-driven optimization of batch crystallization processes [J]. Journal of Process Control, 2013, 23 (2)：179-188.

[21] NIKOLAI K, CHRISTOS G. Dynamic response surface models： a data-driven approach for the analysis of time-varying process outputs[J]. Industrial and Engineering Chemistry Research, 2016, 55 (14)：4022-4034.

[22] ALBADARINA A, YANG Z Y, MANGWANDIA C. Experimental design and batch experiments for optimization of Cr (Ⅵ) removal from aqueous solutions by hydrous cerium oxide nanoparticles [J].Chemical Engineering Research and Design, 2014, 92 (7)： 1354-1362.

[23] 孫偉, 周智, 陸寧云, 等. 基于實驗設計與偏最小二乘逆模型的產品設計方法 [J]. 化工學報, 2010, 61 (1)： 109-115.SUN W, ZHOU Z, LU N Y, et al. A product design strategy based on combination of design of experiment and inversion of partial least square model [J]. CIESC Journal, 2010, 61 (1)： 109-115.

[24] KONG X S, YANG Y, CHEN X. Quality control via model-free optimization for a type of batch process with a short cycle time and low operational cost [J]. Industrial and Engineering Chemistry Research, 2011, 50 (5)： 2994-3003.

[25] ZHU S Q, YANG Y, YANG B, et al. Model-free quality optimization strategy for a batch process with short cycle time and low operational cost [J]. Industrial and Engineering Chemistry Research, 2014,53 (42)： 16384-16396.

[26] ZHAO F, LU N Y, LU J H. Quality control of batch processes using natural gradient based model-free optimization [J]. Industrial and Engineering Chemistry Research, 2014, 53 (44)： 17419-17428.

[27] 葉凌箭, 宋執環, 馬修水. 間歇過程的批間自優化控制 [J]. 化工學報, 2015, 66 (7)： 2573-2580.YE L J, SONG Z H, MA X S. Batch-to-batch self-optimizing control for batch processes [J]. CIESC Journal, 2015, 66 (7)： 2573-2580.

[28] 葉凌箭, 馬修水, 宋執環. 基于輸入軌跡參數化的間歇過程迭代學習控制 [J]. 化工學報, 2016, 67 (3)： 743-750.YE L J, MA X S, SONG Z H. Iterative learning control of batch process with input trajectory parameterization [J]. CIESC Journal,2016, 67 (3)： 743-750.

[29] LI W H, YUE H, CERVANTES S, et al. Recursive PCA for adaptive process monitoring [J]. Journal of Process Control, 2000, 10 (5)：471-486.

[30] 程龍, 王桂增. 改進的遞推主元分析及遞推主元回歸算法 [J]. 控制工程, 2010, 17 (1)： 5-8.CHENG L, WANG G Z. Improved recursive PCA and recursive PCR algorithms [J]. Control Engineering of China, 2010, 17 (1)： 5-8.

A recursive optimization method for batch process trajectories based on similarity of principal components

QIU Li, LUAN Xiaoli, LIU Fei
(Key Laboratory of Advanced Process Control for Light Industry of the Ministry of Education, Jiangnan University,Wuxi 214122, Jiangsu, China)

A recursive optimization method for data-driven operating trajectory, which was based on daily normal operation batches, was proposed for long cycle batch processes. First, original nonlinear optimization was simplified to a high dimensional linear optimization by segmented discretization and high dimensional segmented variables were transformed into lower dimensional one by PCA (principal component analysis) algorithm. Then,snapshot optimization for original operating trajectory was performed according to cosine similarity between time-segmented variables in dimensionality-reduced principal element plane and performance index of the final products. Finally, recursive algorithm for trajectory optimization was developed by consideration of changes in square errors and similarity of time-segmented variables between batches. Application to a batch crystallization process has illustrated effectiveness of this method.

batch processes; trajectory optimization; PCA; cosine similarity; recursive algorithm

date：2016-12-23.

Prof. LUAN Xiaoli, xlluan@jiangnan.edu.cn

supported by the National Natural Science Foundation of China (61473137).

TP 273

A

0438—1157（2017）07—2859—07

10.11949/j.issn.0438-1157.20161797

2016-12-23收到初稿，2017-03-30收到修改稿。

聯系人：欒小麗。

仇力（1992—），男，碩士研究生。

國家自然科學基金項目（61473137）。