ASYMPTOTIC PROPERTIES OF A CLASS OF NONLINEAR STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY
WANG Lin,SUN Lin,HUANG Dong-sheng,WEN Wen-hao
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)
ASYMPTOTIC PROPERTIES OF A CLASS OF NONLINEAR STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY
WANG Lin,SUN Lin,HUANG Dong-sheng,WEN Wen-hao
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)
In this paper,the existence and uniqueness and moment boundedness of solutions to stochastic functional di ff erential equations with in fi nite delay are studied.By using the method of Lyapunov functions and the introduction of probability measures,a new condition which assures that the equations have a unique solution and at the same time the moment boundedness,the moment average in time boundedness of this solution is obtained.Relevant results about the Khasminskii-Mao theorems are generalized.
moment boundedness;Itformula;Brownian motion;in fi nite delay
1 Introduction
Stochastic di ff erential equations are well known to model problems from many areas of science and engineering,wherein quite often the future state of such systems depends not only on the present state but also on its past history(delay)leading to stochastic functional di ff erential equations with delay.In recent years,there was an increasing interest in stochastic functional di ff erential equations with in fi nite delay(ISFDEs in short)under less restrictive conditions.The existence and uniqueness of solutions to ISFDEs were discussed(see[1-4]).Some stabilities such as robustness,attraction,pathwise estimation of solutions to ISFDEs were studied(see[5-13]).It is well known that,in order for a stochastic di ff erential equation to have a unique global solution for any given initial value,the coefficients of the equation are generally required to satisfy the linear growth condition and the local Lipschitz condition or a non-Lipschitz condition and the linear growth condition.In the above two classes of conditions,the linear growth condition plays an important role to suppress thegrowth of the solution and avoid explosion in a fi nite time.However,such results are limited on applications since the coefficients of many important systems which do not satisfy the linear growth condition.It is therefore important to fi nd conditions to guarantee the existence of global solutions under the nonlinear growth coefficients.
Motivated by some results such as[3]and[9],this paper considers a class of stochastic functional di ff erential equations with in fi nite delay whose coefficients are polynomial or controlled by the polynomial functions.We mainly examine the existence and uniqueness of the global solutions of such equations,moment boundedness and moment average boundedness in time.
In this paper,we consider the stochastic functional di ff erential equation with in fi nite delay
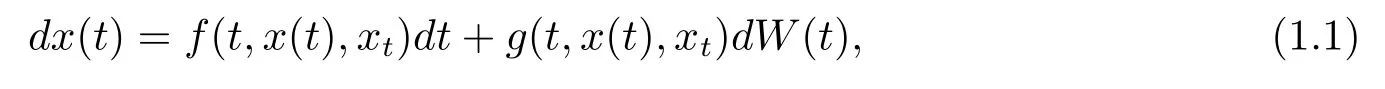
where
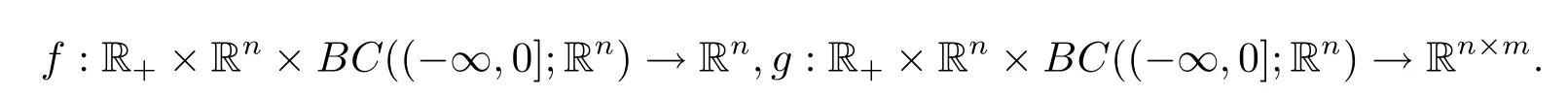
Assumption 1.1Bothfandgare locally Lipschitz continuous.
Denote a solution to eq.(1.1)byx(t).Ifx(t)is defined on(-∞,+∞),we call it a global solution.To show the dependence on the initial dataξ,we writex(t)=x(t,ξ).This paper hopes to fi nd some conditions on the coefficients under which there exists a unique global solutionx(t,ξ)to eq.(1.1)and this solution has properties

and
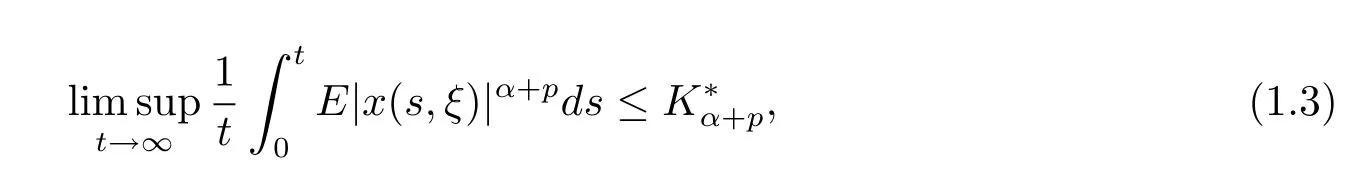
whereα ≥0 andp>0 are proper parameters,Kpandare positive constants independent ofξ.
In order to examine the above problems,a general result is given in Section 3.In Section 4 the general result is discussed in details and two classes of conditions assuring a unique global solution to eq.(1.1)and moment of this solution boundedness are provided in this paper.
2 Preliminaries
First,we give some concepts,notations and stipulations which will be used in this paper.Let{ Ω,F,P}be a complete probability space with a fi ltration{Ft}t≥0satisfying the usual conditions(i.e.,it is right continuous andF0contains allP-null sets).LetW(t)(t≥0)be anm-dimensional Brownian motion defined on the probability space.Denote byC((-∞,0];Rn)the family of continuous functions from(-∞,0]to Rn.Denote byBC((-∞,0];Rn)the family of bounded continuous functions from(-∞,0]to Rnwith the norm

which forms a Banach space,which forms a Banach space.IfAis a vector or matrix,its transpose is denoted byAT.IfAis a matrix,denote its trace norm and operator norm by|A|and‖A‖respectively.Denote the Euclidean norm ofx∈Rnby|x|.Letfor everyi=1,···,n}and0 for everyi=1,···,n}.For any,define
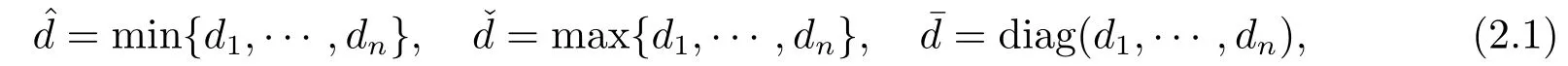
where diag(d1,···,dn)represents then×nmatrix with all elements zero except those on the diagonal which ared1,···,dn.For the positive de fi nite matrixQ,letλmin(Q)be the smallest eigenvalue ofQ.Denoteh(x)byo(|x|α)if for anyα>0,Throughout this paper,when we use the notationo(|x|α),it is always under the condition|x|→+∞.LetLp((-∞,0];Rn)denote all functionsl:(-∞,0]→Rnsuch that
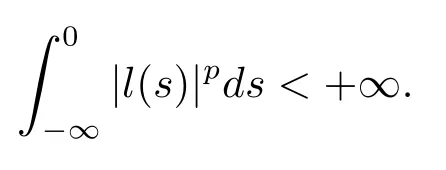
The sign function sgn(x)will be used several times in this paper,and therefore,we provide the de fi nition of the function sgn(x)as follows

For the convenience of reference,several elementary results(see[14])are given as lemmas in the following which will be used frequently.
Lemma 2.1For anyx,y,α≥ 0,β,ε>0,
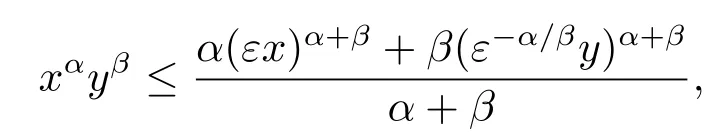
in particular,whenε=1,
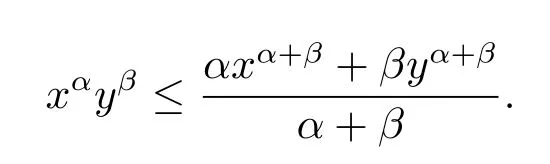
Lemma 2.2For anyx,y∈Rn,0<δ<1,
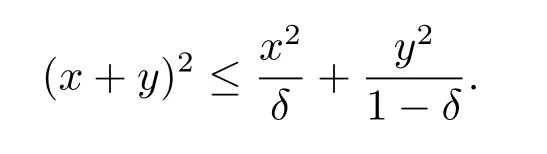
Lemma 2.3For anyh(x)∈C(Rn;R),α,a>0,when|x|→∞,h(x)=o(|x|α),then
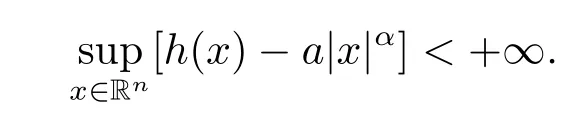
When we use the notationo(|x|α)in this paper,it is always under the condition|x|→+∞.
In addition,throughout this paper,const represents a positive constant,whose precise value or expression is not important.I(x)≤const always implies that I(x)(x∈Rn)has the bounded above.Hence Lemma 2.3 can be rewritten as

Note that the notationo(|x|α)includes the continuity.
Lemma 2.4(see[9])Let
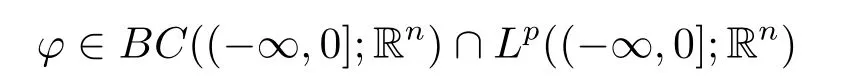
for anyp>0.Then for anyq>p,φ∈Lq((-∞,0];Rn).
LetM0denote all probability measuresμon(-∞,0].For anyε≥0,define
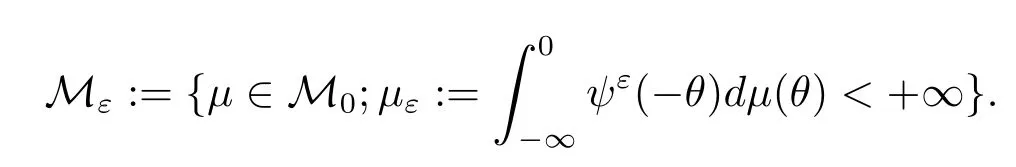
Lemma 2.5(see[9])Fixε0>0.For anyε∈[0,ε0],μεis continuously nondecreasing and satis fi esμε0≥με≥μ0=1 andMε0?Mε?M0.
LetC1,2(R+×Rn;R+)denote the family of all nonnegative functionsV(t,x)on R+×Rnwhich are continuously di ff erential intand twice di ff erential inx,define
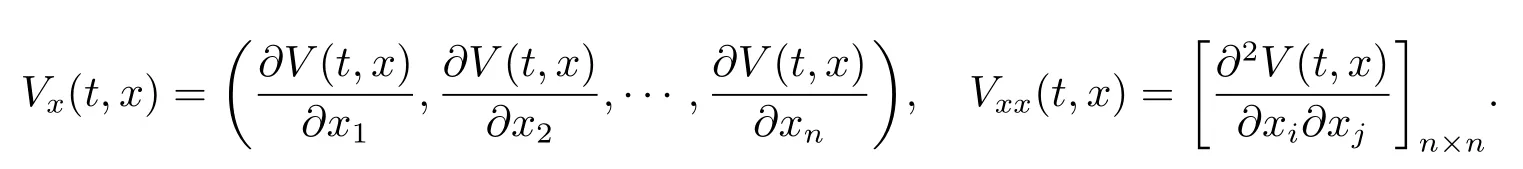
For eq.(1.1),define an operatorLVfromto R by
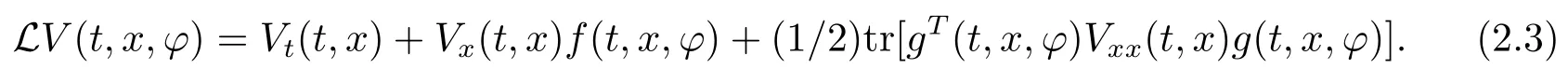
Ifx(t)is a solution to eq.(1.1),then by the Itformula(see[15]),we have
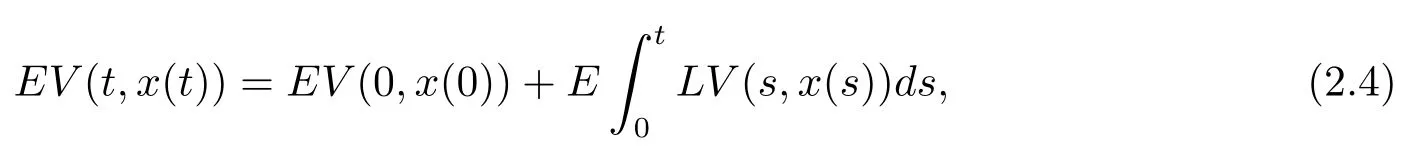
whereLV(t,x(t))=LV(t,x(t),xt).
In this paper,let
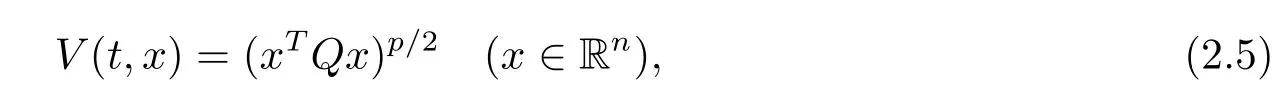
whereQ∈Rn×nare positive de fi nite matrices andp>0.De fi ne

Clearly,we have
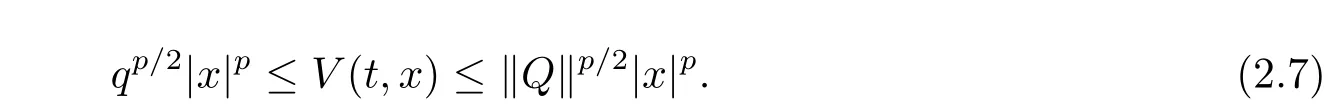
By(2.3),
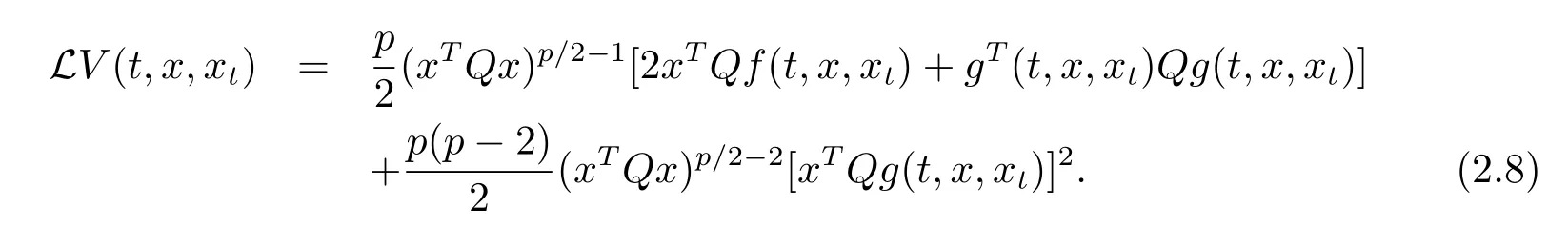
3 An Elementary Lemma
The following lemma plays a key role in this paper.
Lemma 3.1Under Assumption 1.1,if there exist constantsα≥ 0,a,ε,p,K0,Kj,αj>0,probability measuresμj∈Mε(1≤j≤N,j∈N),and a positive de fi nite matrixQ,such that for the functionVdefined in(2.5),φ∈BC((-∞,0];Rn),
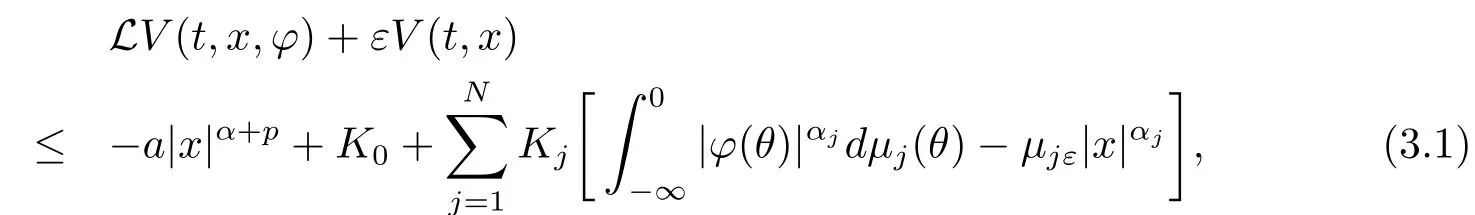
then for any initial data
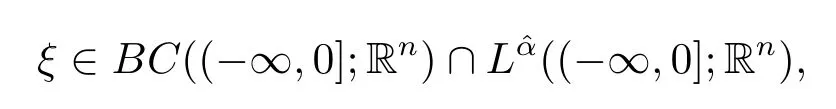
ProofFirst,note that condition(3.1)includes the following three inequalities
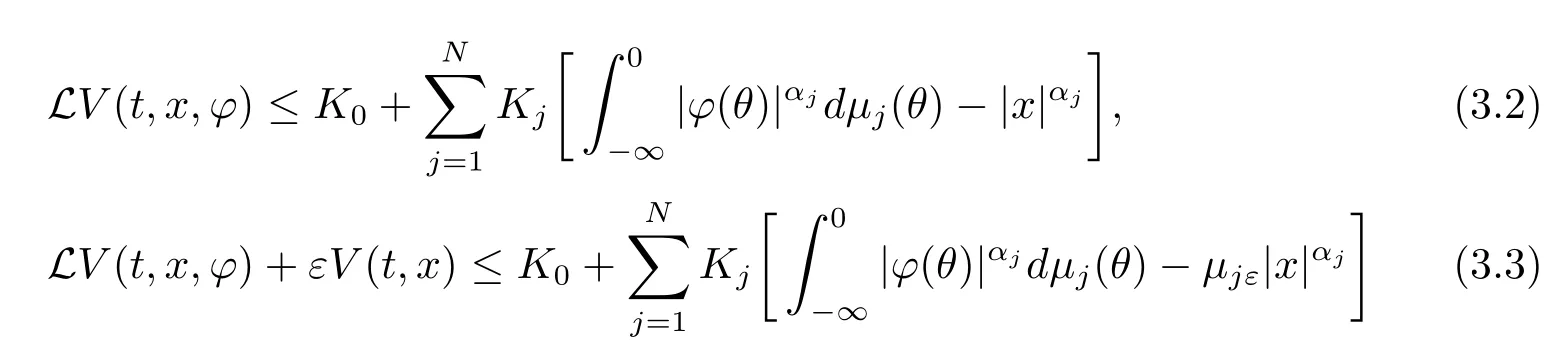
and
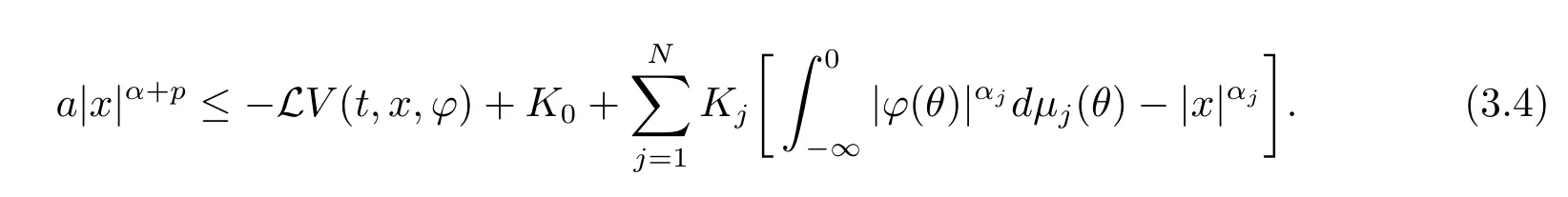
For any given initial dataξ∈BC((-∞,0];Rn)∩L?α((-∞,0];Rn),we will divide the whole proof into three steps.
Step 1Let us fi rst show the existence of the global solutionx(t,ξ).Under Assumption 1.1,eq.(1.1)admits a unique maximal local solutionx(t)for-∞<t<σ,whereσis the explosion time.De fi ne the stopping time
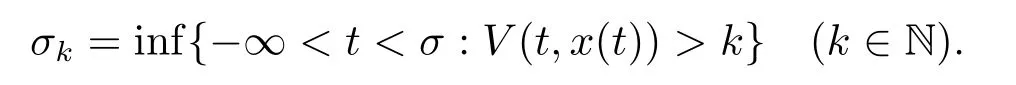
Sinceξis bounded,whenkis sufficiently large such thatV(θ,x(θ))≤kfor-∞<θ≤0,thusσk≥ 0.Ifσ<+∞,whent→σ,x(t)may explode.Hence
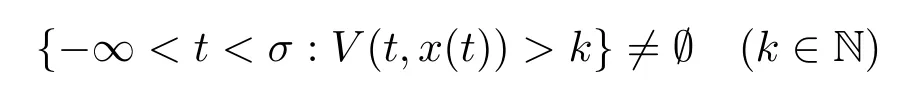
shows thatσk≤σ.Thus,we may assume 0≤σk≤σ(?k∈N).Obviously,σkis increasing andσk→σ+∞≤σ(k→+∞)a.s..If we can showσ+∞=+∞,thenσ=+∞a.s.,which implies thatx(t)is a global solution.This is also to prove that,for anyt>0,P(σk≤t)→0 ask→+∞.
Fixt>0.Now we prove thatP(σk≤t)→0(k→+∞).First note that ifσk<+∞,then by the continuity ofx(t),V(σk,x(σk))≥k.Hence,by(2.4)and(3.2),Lemmas 2.4 and 2.5,we can compute that
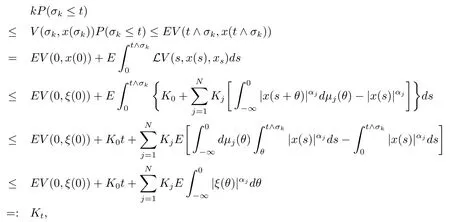
whereKtis a positive constant independent ofk.Therefore we have
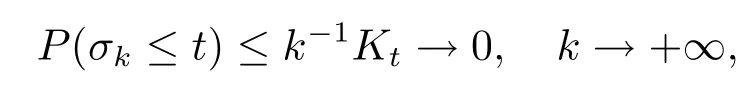
which shows thatx(t)=x(t,ξ)is a global solution to eq.(1.1).
Step 2Let us now show inequality(1.2).Applying the Itformula toeεtV(t,x(t)),by(2.4)and(3.3),Lemmas 2.4 and 2.5,yields

wherecis a positive constant independent oftandK=ε-1K0is a positive constant independent ofξ.Hence,we have.Then the required assertion(1.2)follows from(2.7).
Step 3Finally,let us show assertion(1.3).Using(3.4),Lemmas 2.4 and 2.5,we obtain that
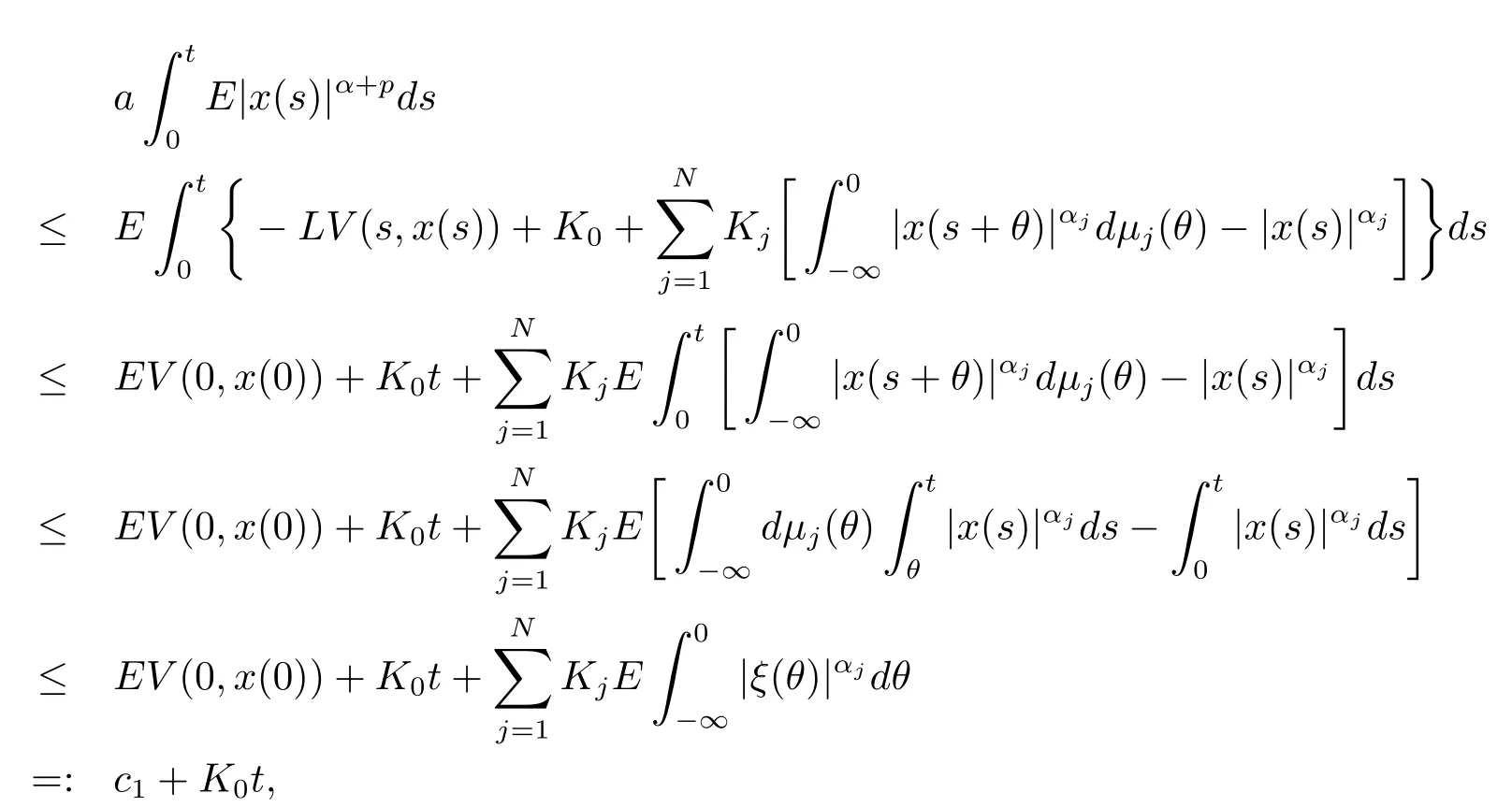
wherec1is a positive constant independent oft.Assertion(1.3)follows directly.The proof is therefore completed.
Denote the left hand of(3.1)by Φ and establish the inequality
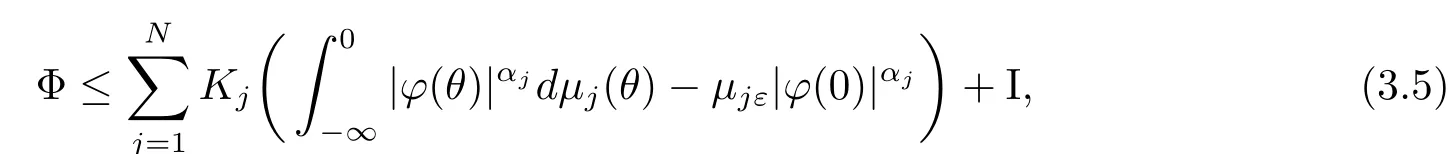
where

andα≥ 0,Kj,αj,a,p>0.By Lemma 2.3,
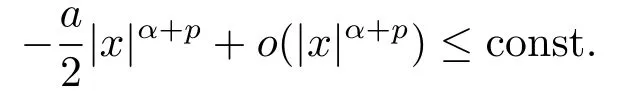
This,together with(3.6),yields
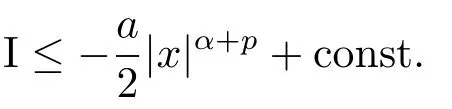
Substituting this into(3.5)shows that condition(3.1)is satis fi ed.To get(3.5)and(3.6),some conditions are imposed on the coefficientsfandg.These conditions are considered in the next section.
4 Main Results
Recall Φ to denote the left hand of(3.1).By(2.8),
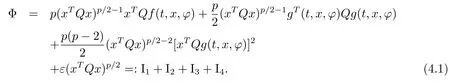
We fi rst list the following conditions that we will need
(H1)There existα,κ,>0,the probability measureμ ∈Mεon(-∞,0],a positivede fi nite matrixQ,h(x)∈C(Rn;R),such that
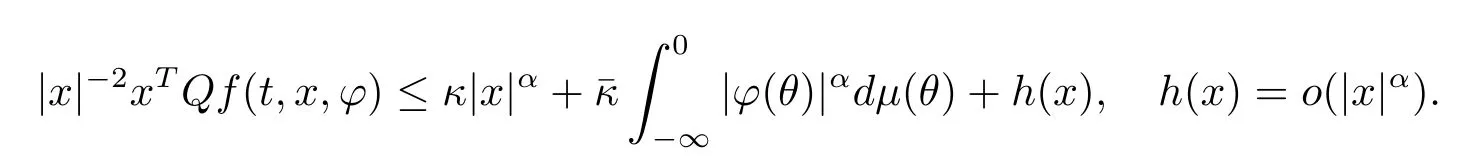
(H2)There existβ,λ,>0,the probability measureν ∈Mεon(-∞,0],h(x)∈C(Rn;R),such that
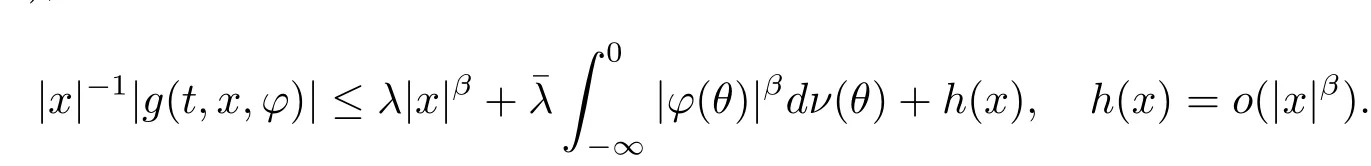
(H3)There exista,β,σ>0,the probability measure∈Mεon(-∞,0],a positivede fi nite matrixQ,h(x)∈C(Rn;R),such that
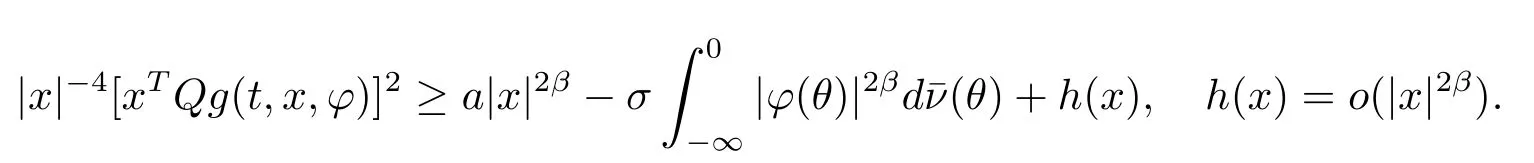
(F1)There exista,α,σ>0,the probability measure∈Mεon[-∞,0],a positivede fi nite matrixQ,h(x)∈C(Rn;R),such that
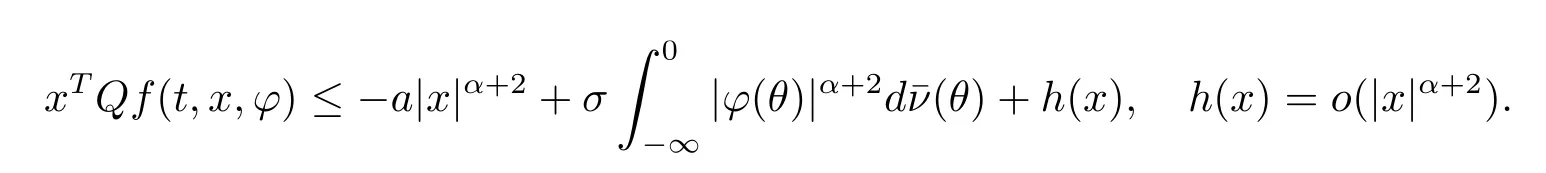
(F2)There existβ,λ,>0,the probability measureν ∈Mεon[-∞,0],h(x)∈C(Rn;R),such that
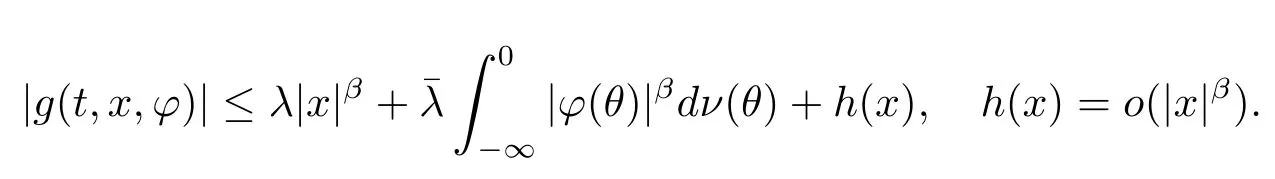
The continuity ofh(x)is important in all these conditions.
Now we can state one of our main results in this paper.
Theorem 4.1Under Assumption 1.1,if conditions(H1)-(H3)hold,α ≤2βand

whereqandRare as defined in(2.6),then for any given initial dataξ∈BC((-∞,0];Rn)∩L?α((-∞,0];Rn),there exists a unique global solutionx(t,ξ)to eq.(1.1).Ifp∈(0,2)satis fi es
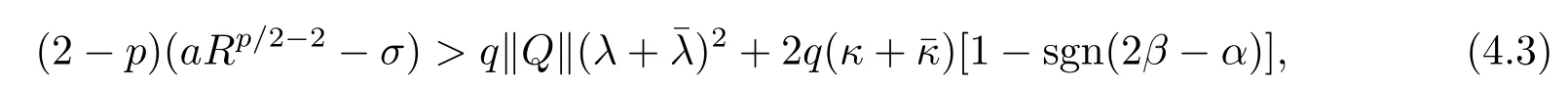
then the solutionx(t,ξ)has properties(1.2)and(1.3),except thatαis replaced by 2β.
ProofLetVbe as defined in(2.5),p∈(0,2),andε>0 be sufficiently small.Now we estimate I1-I4,respectively.First,by condition(H1)and Lemma 2.1,
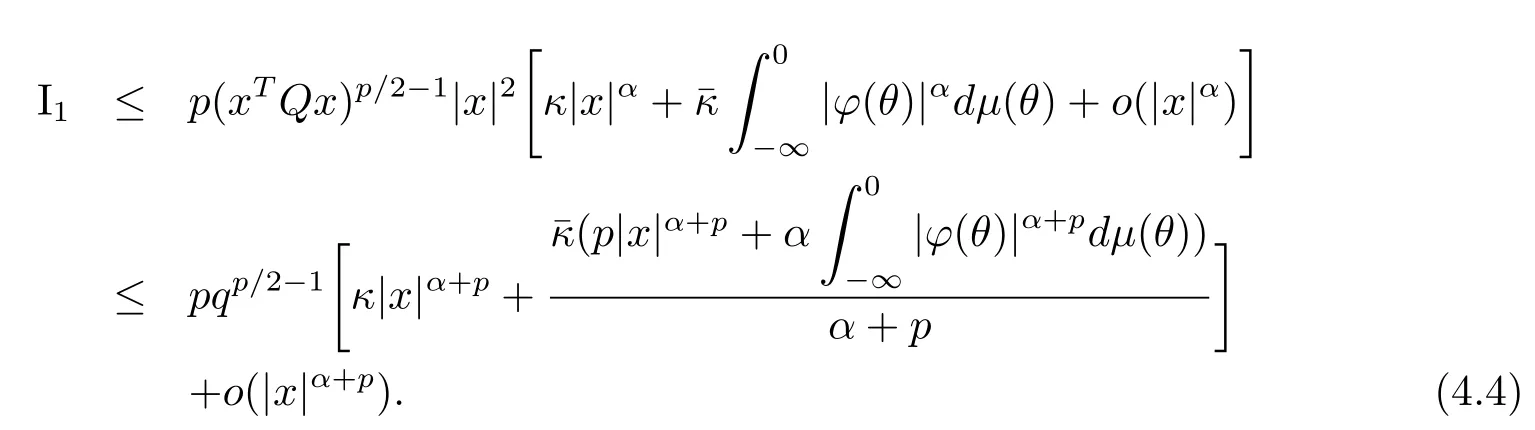
Next,by condition(H2)and Lemma 2.2,for anyu,δ∈(0,1),
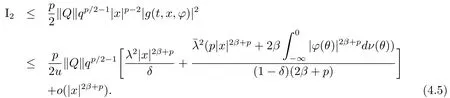
Noting thatp<2 and by condition(H3),we have
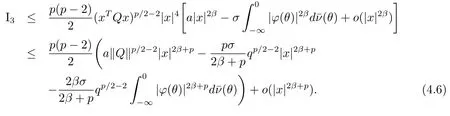
It is easy to see thatI4=o(|φ(0)|2β+p).Then substituting(4.4)-(4.6)into(4.1)yields
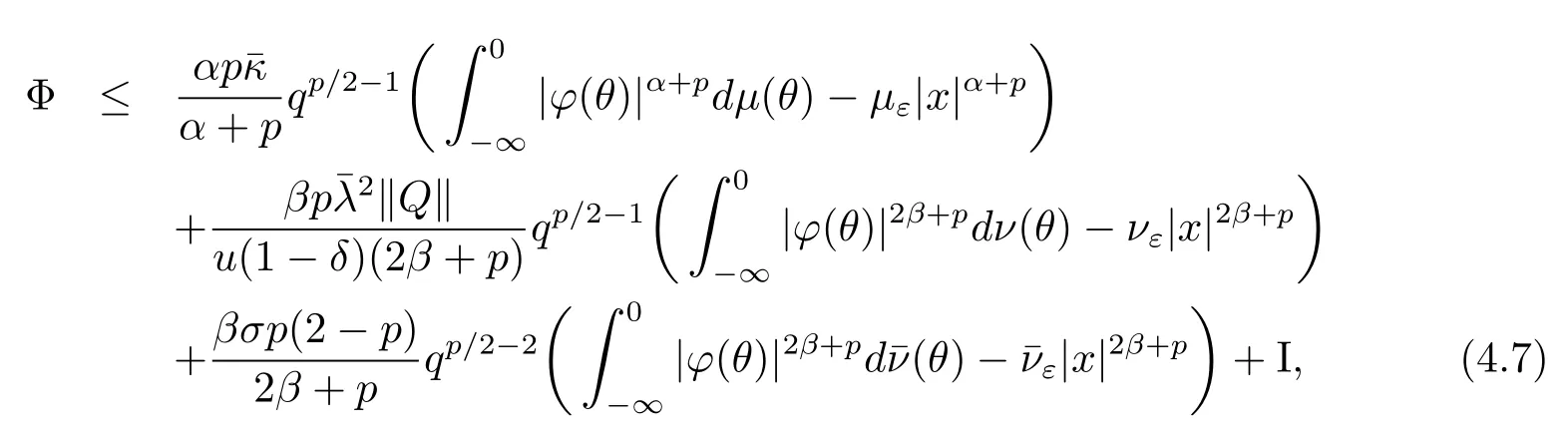
whose form is similar to(3.5),where
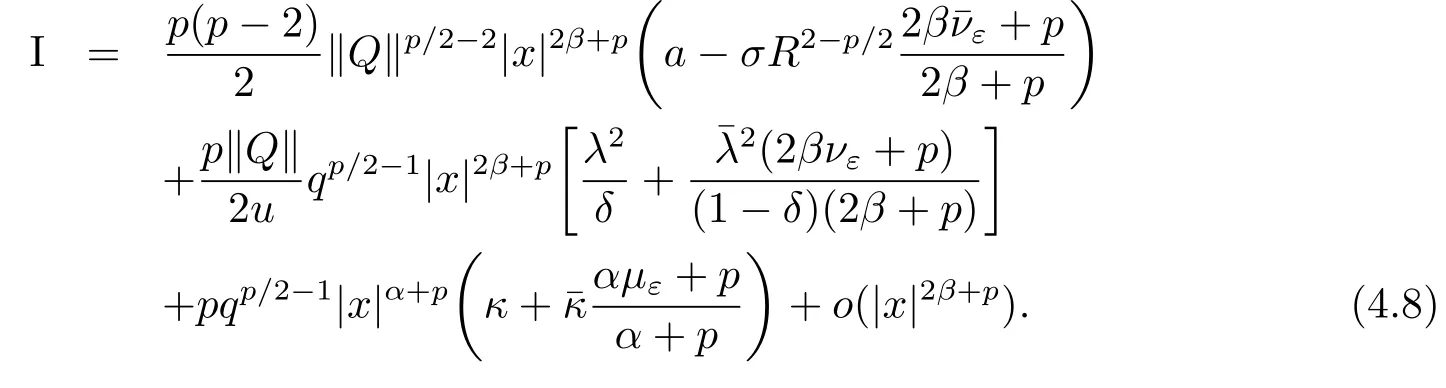
Then we consider(4.8)under di ff erent cases.First,let condition(4.3)hold.Ifα<2β,then by(4.8),
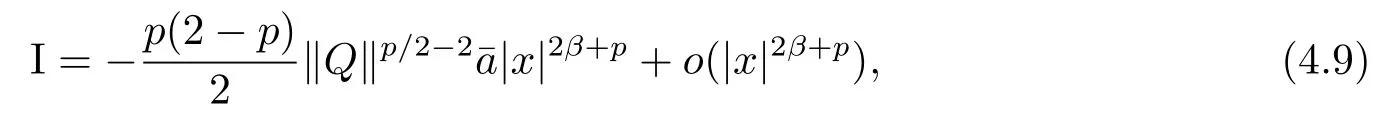
where
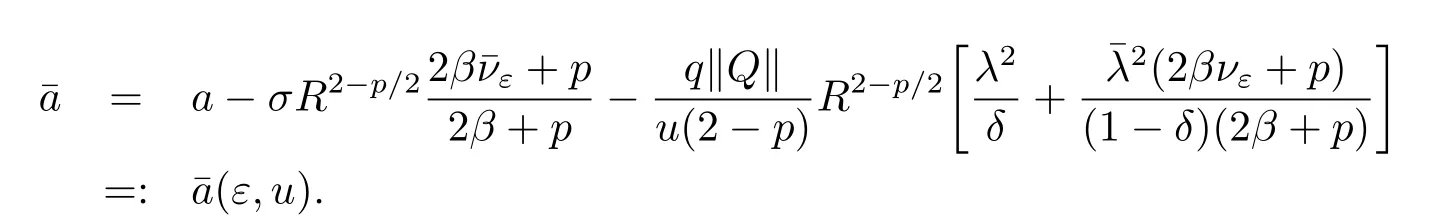
Therefore
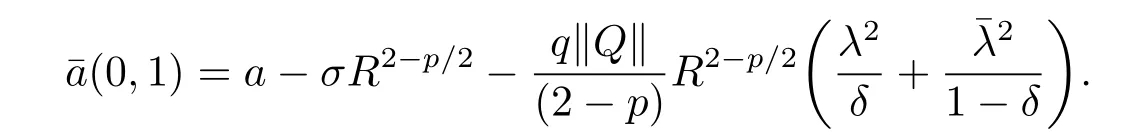
Letλ,>0(otherwise,we can compute directly).Choosingδ=λ/(λ+)∈(0,1),minimizing the right hand of the above formula and by(4.3),we obtain
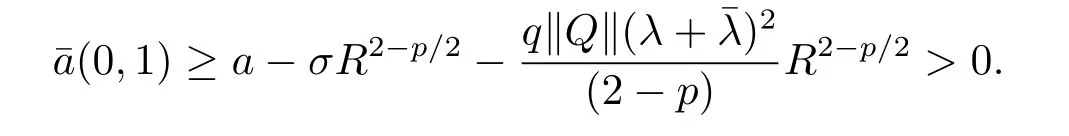
Sinceεis sufficiently small,letuapproach to 1 adequately such that>0.Therefore,the form of(4.9)is similar to(3.6).
Ifα=2β,then by(4.8),

where
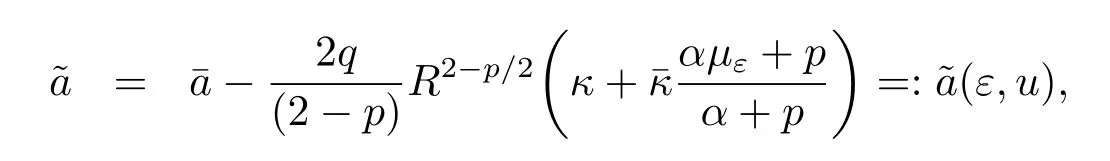
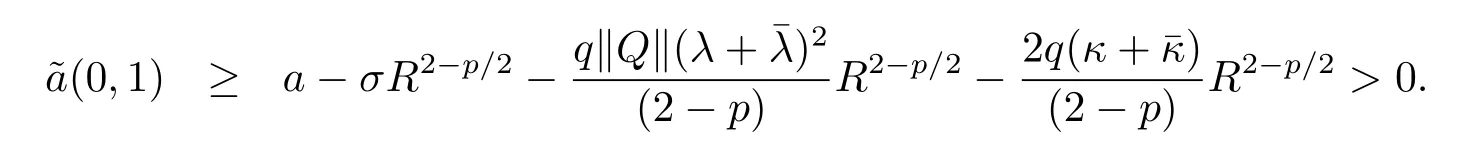
If condition(4.2)holds andp>0 is sufficiently small,then condition(4.3)holds.Therefore,there exists a unique global solutionx(t,ξ)(?ξ∈BC((-∞,0];Rn)∩L?α((-∞,0];Rn)to eq.(1.1)).The proof is completed.
If we impose condition(F1)on functionf,we have
Theorem 4.2Under Assumption 1.1,if conditions(F1)and(F2)hold,p≥2,α≥2β-2 and
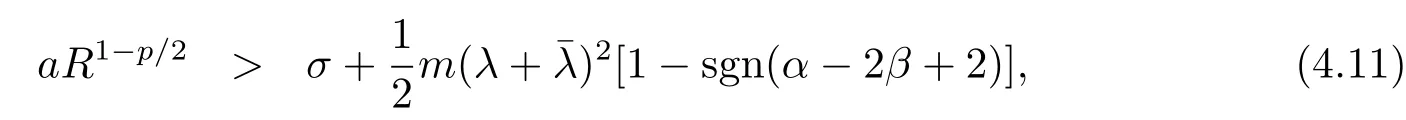
whereRis as defined in(2.6),m=‖Q‖[1+R(p-2)],then for any initial dataξ∈BC((-∞,0];Rn)∩L((-∞,0];Rn),there exists a unique global solutionx(t,ξ)to eq.(1.1)and this solution satis fi es(1.2)and(1.3).
ProofThe proof is similar to that of Theorem 4.1,so we omit it.
[1]Wei Fengying,Wang Ke.The existence and uniqueness of the solution for stochastic functional di ff erential equations with in fi nite delay[J].J.Math.Anal.Appl.,2007,331:516-531.
[2]Ren Yong,Lu Shiping,Xia Ningmao.Remarks on the existence and uniqueness of the solutions to stochastic functional di ff erential equations with in fi nite delay[J].J.Comput.Appl.Math.,2008,220(1):364-372.
[3]Wang Lin,Wu Fuke.Existence,uniqueness and asymptotic properties of a class of nonlinear stochastic di ff erential delay equations with Markovian switching[J].Stoc.Dyns.,2009,9(2):253-275.
[4]Xu Yong,Hu Shigeng.The existence and uniqueness of the solution for neutral stochastic functional di ff erential equations with in fi nite delay in abstract space[J].Acta.Appl.,2009,doi:10.1007/s 10440-009-9465-x.
[5]Hu Yangzi,Wu Fuke,Huang Chengming.Robustness of exponential stability of a class of stochastic functional di ff erential equations with in fi nite delay[J].Auto.,2009,45:2577-2584.
[6]Wu Fuke,Xu Yong.Stochastic Lotka-Volterra population dynamics with in fi nite delay[J].SIAM J.Appl.Math.,2009,70:641-657.
[7]Zhou Shaobo,Wang Zhiyong,Feng Dan.Stochastic functional di ff erential equations with in fi nite delay[J].J.Math.Anal.Appl.,2009,357:416-426.
[8]Liu Yue,Meng Xuejing,Wu Fuke.Some stability criteria of stochastic functional di ff erential equations with in fi nite delay[J].J.Appl.Math.Stoc.Anal.,2010,doi:10.1155/2010/875908.
[9]Wu Fuke,Hu Shigeng,Huang Chengming.Robustness of general decay stability of nonlinear neutral stochastic functional di ff erential equations with in fi nite delay[J].Sys.Contr.Lett.,2010,59:195-202.
[10]Meng Xuejing,Hu Shigeng,Wu Ping.Pathwise estimation of stochastic di ff erential equations with unbounded delay and its application to stochastic pantograph equations[J].Acta.Appi.Math.,2011,113:231-246.
[11]Wu Fuke,Hu Shigeng.Attraction,stability and robustness for stochastic functional di ff erential equations with in fi nite delay[J].Auto.,2011,47:2224-2232.
[12]Yue Chaohui.Neutral stochastic functional di ff erential equations with in fi nite delay and Poisson jumps in the Cg space[J].Appl.Math.Comp.,2014,237:595-604.
[13]Guo Ying,Su Huan,Ding Xiaohua,Wang Ke.Global stochastic stability analysis for stochastic neural networks with in fi nite delay and Markovian switching[J].Appl.Math.Comp.,2014,245:53-65.
[14]Beckenbach E F,Bellman R.Inequalities[M].Berlin:Springer-Verlag,1961.
[15]Mao Xuerong.Stochastic di ff erential equations and applications[M].Chichester:Ellis Horwood,1997.
無限時滯的隨機(jī)泛函微分方程解的漸近性質(zhì)
王 琳,孫 琳,黃冬生,溫文豪
(廣東工業(yè)大學(xué)應(yīng)用數(shù)學(xué)學(xué)院,廣東廣州 510520)
本文研究了無限時滯隨機(jī)泛函微分方程解的存在唯一性,矩有界性的問題.利用Lyapunov函數(shù)法以及概率測度的引入得到了確保方程解在唯一、矩有界、時間平均矩有界同時成立的一個新的條件.推廣了Khasminskii-Mao定理的相關(guān)結(jié)果.
矩有界;伊藤公式;Brown運(yùn)動;無限時滯
O211.63
on:34K50;60H10
A
0255-7797(2017)04-0769-12
date:2015-06-04Accepted date:2015-11-18
Supported by National Natural Science Foundation of China(11201083);Natural Science Foundation of Guangdong Province(S2013010016270);Foundation of College Students Innovation Project(XJ201511845094).
Biography:Wang Lin(1980-),female,born at Xinyang,Henan,lecturer,major in the theories of stochastic dynamic system.
- 數(shù)學(xué)雜志的其它文章
- THE GROWTH ON ENTIRE SOLUTIONS OF FERMAT TYPE Q-DIFFERENCE DIFFERENTIAL EQUATIONS
- A MODIFIED BIC TUNING PARAMETER SELECTOR FOR SICA-PENALIZED COX REGRESSION MODELS WITH DIVERGING DIMENSIONALITY
- FINITE GROUPS WHOSE ALL MAXIMAL SUBGROUPS ARE SMSN-GROUPS
- GLOBAL BOUNDEDNESS OF SOLUTIONS IN A BEDDINGTON-DEANGELIS PREDATOR-PREY DIFFUSION MODEL WITH PREY-TAXIS
- ON PROJECTIVE RICCI FLAT KROPINA METRICS
- 態(tài)R0代數(shù)

