態(tài)R0代數(shù)

秦玉靜,辛小龍,賀鵬飛

(1.西北大學數(shù)學學院,陜西西安710127)

(2.陜西師范大學數(shù)學與信息科學學院,陜西西安710119)

態(tài)R0代數(shù)

秦玉靜1,辛小龍1,賀鵬飛2

(1.西北大學數(shù)學學院,陜西西安710127)

(2.陜西師范大學數(shù)學與信息科學學院,陜西西安710119)

本文研究了R0代數(shù)上有關態(tài)算子的問題.利用MV-代數(shù)上內(nèi)態(tài)的引入方法引入了態(tài)算子,定義了態(tài)R0代數(shù),它是R0代數(shù)的一般化.給出了一些非平凡態(tài)R0代數(shù)的例子并討論了態(tài)R0代數(shù)的一些基本性質.在此基礎上給出了態(tài)濾子和態(tài)局部R0代數(shù)的概念,并利用態(tài)濾子刻畫了態(tài)局部R0代數(shù).推廣了局部R0代數(shù)的相關理論.

R0代數(shù);態(tài)R0代數(shù);態(tài)濾子;態(tài)局部

1 引言

多值邏輯系統(tǒng)是20世紀30年代Lukasiewicz提出的.隨著20世紀70年代模糊集概念的提出,模糊邏輯與模糊推理理論得到了發(fā)展.基于對模糊邏輯與經(jīng)典邏輯本質區(qū)別的分析,1997年,王國俊[1]提出了模糊命題的一種形式演繹系統(tǒng)￡?,為了系統(tǒng)研究￡?,王國俊[2]引入了一種新的邏輯代數(shù)-R0代數(shù).這為這類演繹系統(tǒng)的研究提供了代數(shù)模型.隨后,很多學者[3-5]都對R0代數(shù)進行了研究.

作為多值邏輯中命題真值的平均度,1995年Mundici[6]提出了MV代數(shù)上態(tài)的概念.近年來,國內(nèi)外很多學者致力于邏輯代數(shù)上態(tài)理論的研究.例如,2008年,劉練珍[14]研究了R0代數(shù)上的態(tài)存在問題.2007年,Flaminio和Montagna[7]用一種新的方法研究了MV代數(shù)上的態(tài).他們在MV代數(shù)上定義了一個一元運算σ(稱為內(nèi)部態(tài)或者態(tài)算子),它是態(tài)的推廣.隨后,態(tài)算子在其他代數(shù)結構中進行了研究.例如,2011年Ciungu等[8]提出了態(tài)BL代數(shù),它是態(tài)MV代數(shù)的推廣.2015年,賀鵬飛、辛小龍[13]提出了態(tài)residuated lattices并研究了其相關性質.本文提出了態(tài)R0代數(shù)的定義,研究了它的性質,又定義了態(tài)濾子和態(tài)局部R0代數(shù)的概念,并利用態(tài)濾子刻畫了態(tài)局部R0代數(shù).

2 預備知識

定義2.1[2]設L=(L,∧,∨,′,→,0,1)是 (2,2,1,2,0,0) 型代數(shù),若

(1)(L,∧,∨,0,1)是一個有界分配格;

(2)′是關于序≤而言的逆序對合對應;

(3)對于L中的任意元素x,y,z,有

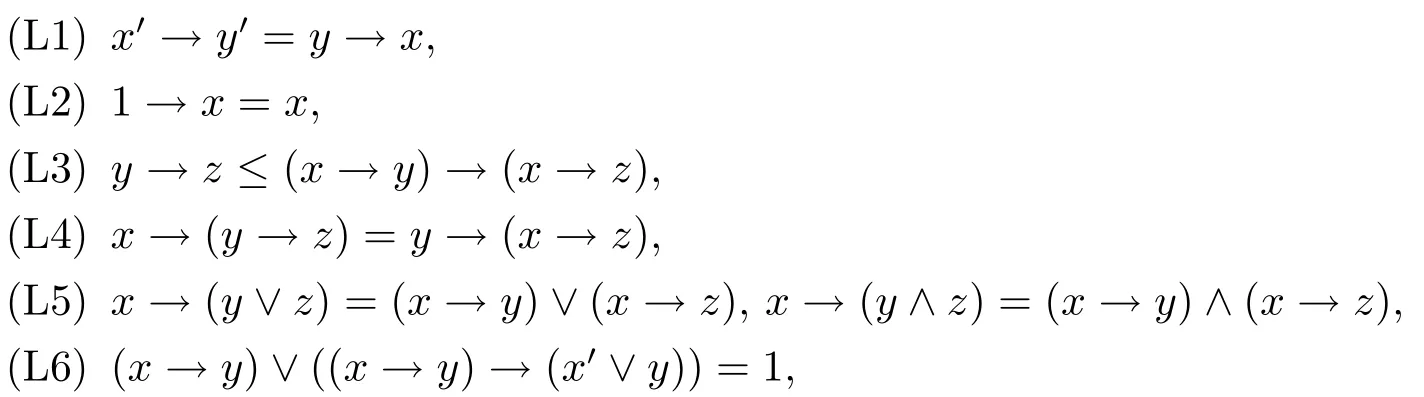
則稱(L,∧,∨,′,→,0,1)為R0代數(shù).以下簡記為L.

在R0代數(shù)L中定義序關系”≤”為x≤y當且僅當x→y=1.

性質2.2[2]設L是R0代數(shù),則以下結論成立：對任意的x,y,z∈L,

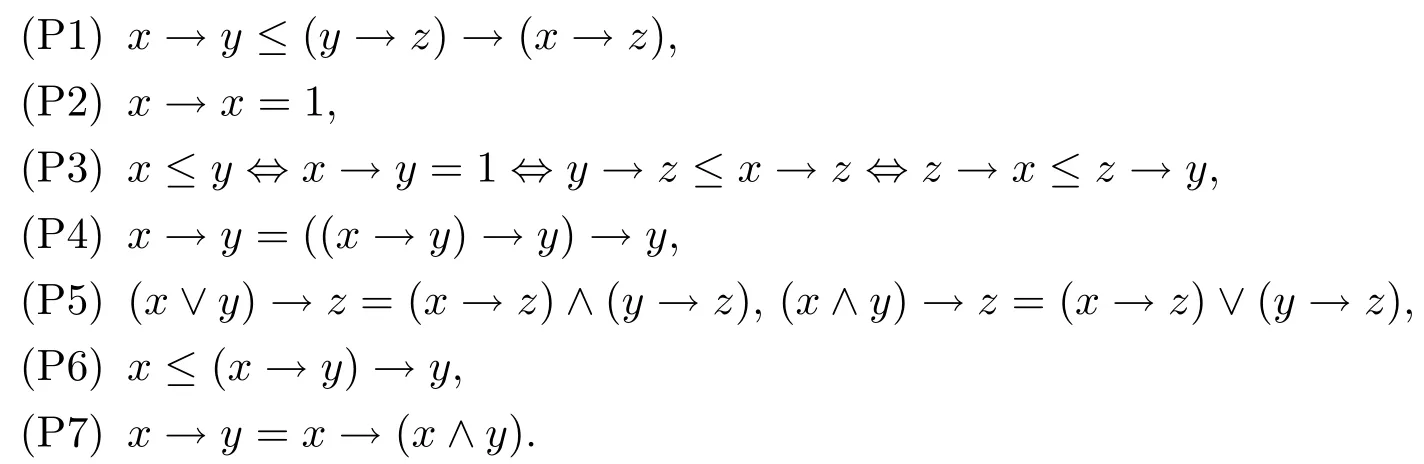
性質2.3[2]設L是R0代數(shù),在L上定義x?y=(x→y′)′,則有對任意的x,y,z∈L,

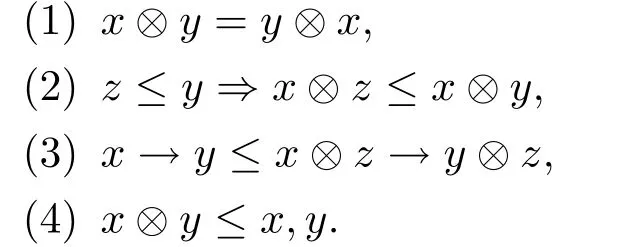
定義2.4[9]設L是R0代數(shù),F是L的非空子集,若以下條件成立：對任意的x,y∈F,

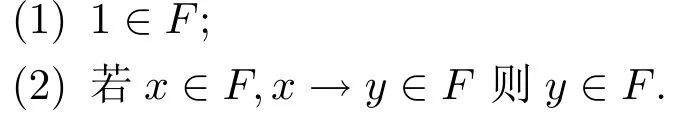
則稱F為L的濾子.

設L是R0代數(shù),F為L的濾子.若,則稱F為真濾子.顯然,F是真濾子當且僅當0當且僅當對任意的x∈L,x和x′不能同時屬于F.若E是任意一個濾子,且F?E,有E=F或E=L,則稱真濾子F為極大濾子.

引理2.5[10]設L是R0代數(shù),F是L的非空子集,則F是L的濾子以下條件成立：對任意的x,y∈F,

(1)1∈F,

(2)若x∈F,x≤y,則y∈F,

(3)若x,y∈F,則x?y∈F.

推論2.6[10]設L是R0代數(shù),F是L的濾子,定義二元關系RF為xRFy當且僅當x→y∈F和y→x∈F.則

(1)RF為L上的同余關系,

(2)L/F為一個R0代數(shù),這里[x]表示x所在的RF等價類并且L/F={ [x]|x∈L}.

定義2.7[9]設L是R0代數(shù),x∈L,使xm=0成立的最小自然數(shù)m叫做元素x的階,記為ord(x).若這樣的m不存在,則稱x的階為無限,即ord(x)=∞.

引理2.8[11]設L是R0代數(shù),X是L的非空子集,稱包含X的最小濾子為由X生成的濾子,記為〈X〉,則〈X〉={x∈L|x≥x1?x2? ···?xn,存在x1,x2···xn∈X}.記L的所有濾子集為F(L),且F(L)(關于包含關系)可構成完備格.

引理2.9[9]設L為R0代數(shù),F為L的任意一個真濾子,則F可延拓為一個極大濾子.

定義2.10[12]設L為R0代數(shù),若L有唯一的極大濾子,則稱L為局部的.

3 態(tài)R0代數(shù)

定義3.1設L是R0代數(shù),σ：L→L為L上的自映射.若σ滿足：對任意的x,y∈L,

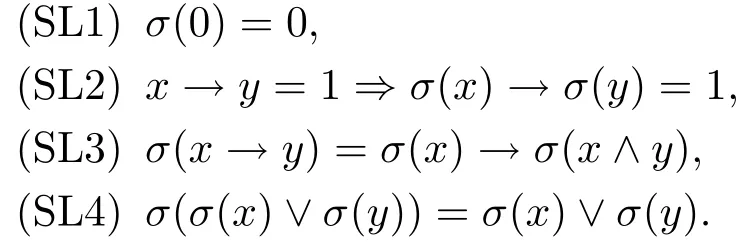
則稱σ為L上的態(tài)算子,此時稱(L;σ)為態(tài)R0代數(shù).

設σ為L上的任意的態(tài)算子,Ker(σ)={x∈L|σ(x)=1}.若Ker(σ)={ 1},則稱σ為忠實的.

例3.2設L為R0代數(shù),由性質2.2可知,idL為L上的態(tài)算子.因此(L;idL)為態(tài)R0代數(shù),即一個R0代數(shù)L可以看成是一個態(tài)R0代數(shù).

例3.3設L={ 0,a,b,c,d,e,f,g,1},L上的偏序關系為0≤a≤c,d≤f≤1,0≤b≤d,e≤g≤1,其上的二元運算→和一元運算′的定義如下表所示

→ 0 a b c d e f g 1 0 1 1 1 1 1 1 1 1 1a g 1 g 1 1 g 1 1 1b f f 1 f 1 1 1 1 1c e g e 1 g e 1 g 1d d f g f 1 g 1 1 1e c c f c f 1 f 1 1f b d e f g e 1 g 1g a c d c f g f 1 1 1 0 a b c d e f g 1x 0 a b c d e f g 1x′ 1 g f e d c b a 0

容易驗證(L,∧,∨,′,→,0,1)是R0代數(shù).在L上定義σ如下

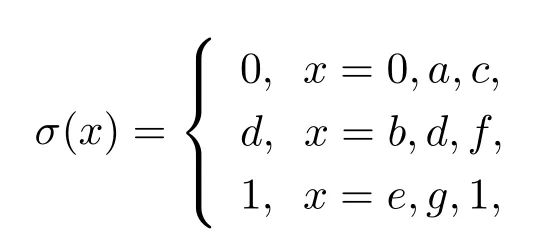
則容易驗證σ是L上的態(tài)算子,即(L;σ)是態(tài)R0代數(shù).

性質3.4設(L;σ)為態(tài)R0代數(shù),則以下結論成立：對任意的x,y∈L,

(1)σ(1)=1,

(2)x≤y?σ(x)≤σ(y),

(3)σ(x′)=(σ(x))′,

(4)σσ(x)=σ(x),

(5)σ(σ(x)∧ σ(y))=σ(x)∧σ(y),

(6)σ(σ(x)→σ(y))=σ(x)→σ(y),

(7)σ(σ(x)? σ(y))=σ(x)? σ(y),

(8)σ(x→y)≤σ(x)→σ(y).特別地,若x,y可比較,則σ(x→y)=σ(x)→σ(y),

(9)若σ是忠實的,則x＜y?σ(x)＜σ(y),

(10)σ(L)=Fix(σ),這里 Fix(σ)={x∈L|σ(x)=x},

(11)σ(x?y)≥σ(x)?σ(y).特別地,若x,y可比較,則σ(x?y)=σ(x)?σ(y),

(12)Ker(σ)是L的濾子,

(13)σ(L)是L的子代數(shù).

證 (1)由(SL2)可得σ(0→1)=σ(0)→σ(0∧1),即σ(1)=σ(0)→σ(0)=1.

(2)由x≤y可得x→y=1,又由(SL2)可知σ(x)→σ(y)=1即σ(x)≤σ(y).

(3) 由 (SL3)可知σ(x′)=σ(x→0)=σ(x)→σ(x∧0)=σ(x)→σ(0)=(σ(x))′.

(4) 由(SL1)和(SL4)可得σ(σ(x)∨ σ(0))=σ(x)∨σ(0),即σσ(x)=σ(x).

(5)由(SL4)和(3),

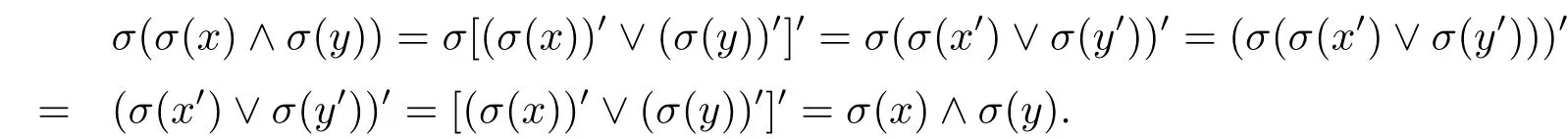
(6)由(SL3),(4)和(5)可得

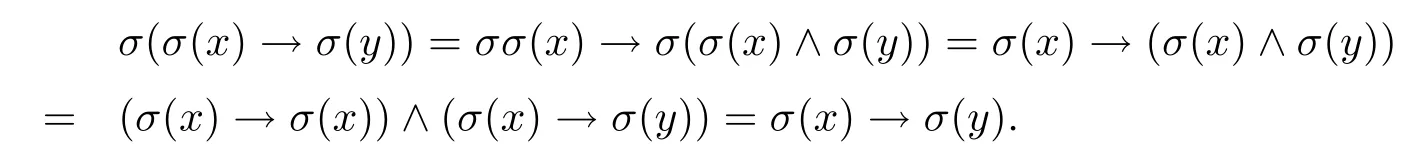
(7)由(3)和(6)可得

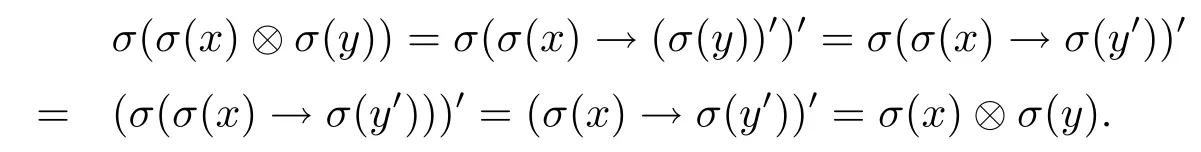
(8)由于x∧y≤y,即(x∧y)→y=1,由(SL2)可得σ(x∧y)→σ(y)=1即σ(x∧y)≤σ(y).由(P3)可知σ(x)→σ(x∧y)≤σ(x)→σ(y),又根據(jù)(SL3),σ(x→y)=σ(x)→σ(x∧y)≤σ(x)→σ(y).

若x≤y,則σ(x)≤σ(y)即σ(x)→σ(y)=1,σ(x→y)=σ(1)-1,所以σ(x→y)=σ(x)→σ(y).

若y≤x,則x∧y=y.由(SL3)可知,σ(x→y)=σ(x)→σ(x∧y)=σ(x)→σ(y).

(9)由x＜y可得σ(x)≤σ(y).假設σ(x)=σ(y),由 (SL3),σ(y→x)=σ(y)→σ(y∧x)=σ(y)→σ(x)=1即y→x∈Ker(σ)={ 1},則y→x=1,即y≤x,與條件矛盾.所以σ(x)＜σ(y).

(10)若對任意y∈ σ(L),則存在x∈L使得y=σ(x),σ(y)=σσ(x)=σ(x)=y,即y∈Fix(σ).若對任意y∈Fix(σ),即σ(y)=y,則y∈σ(L).所以σ(L)=Fix(σ).

(11) 由 (P3),(3)和 (8)可得σ(x?y)=σ(x→y′)′=(σ(x→y′))′≥ (σ(x)→σ(y′))′=σ(x)?σ(y).特別地,若x,y可比較,則由(3)和(8)得σ(x?y)=σ(x→y′)′=(σ(x→y′))′=(σ(x)→σ(y′))′=σ(x)?σ(y).

(12)由σ(1)=1可知1∈Ker(σ).任意x,y∈L,若x,x→y∈Ker(σ),則有σ(x)=1,σ(x→y)=1.σ(x)→σ(y)=1→σ(y)=σ(y),由 (7),σ(y)=σ(x)→σ(y)≥σ(x→y)=1,即σ(y)=1,所以y∈Ker(σ).則Ker(σ)為L的濾子.

(13)由(L1),(L4)和(1),(3),(5),(6)知σ(L)對運算∧,∨,′,→且對0,1封閉.所以σ(L)為L的子代數(shù).

4 態(tài)R0代數(shù)上的態(tài)濾子

定義4.1設(L;σ)是態(tài)R0代數(shù),F為L的濾子.若對任意的x∈F,有σ(x)∈F,則稱F為(L;σ)的態(tài)濾子.設F為真態(tài)濾子,E是任意一個態(tài)濾子,若F?E,有E=F或E=L,則稱F為(L;σ)的極大態(tài)濾子.記SF[L]為(L;σ)的所有態(tài)濾子的集合.

例4.2設F1={e,g,1},F2={c,f,1}為例3.2中L的子集,顯然,F1,F2都是L的濾子.容易驗證F1是(L;σ)的態(tài)濾子.而在F2中,c,f∈F2但σ(c)=0/∈F2,σ(f)=2,所以F2不是(L;σ)的態(tài)濾子.

設(L;σ)是態(tài)R0代數(shù),X是L的非空子集,稱包含X的最小態(tài)濾子為由X生成的態(tài)濾子,記為〈X〉σ.

定理4.3 設(L;σ)為態(tài)R0代數(shù),X是L的非空子集.則〈X〉σ={x∈L|x≥(x1?σ(x1))n1?···?(xk?σ(xk))nk,xi∈X,ni≥ 1,k≥ 1}.

證證明和文獻[8]中定理5.4的證明類似.

引理4.4設(L;σ)是態(tài)R0代數(shù),F為(L;σ)的真態(tài)濾子,則F為極大態(tài)濾子當且僅當對任意的x/∈F,存在正整數(shù)n≥1使得(σ(x)n)′∈F.

證證明和文獻[8]中定理5.4的證明類似.

定義4.5設(L;σ)為態(tài)R0代數(shù),若(L;σ)有唯一的極大態(tài)濾子,則稱(L;σ)為態(tài)局部的.

設(L;σ)是態(tài)R0代數(shù),定義D(L;σ)={x∈L|?n≥ 1,(σ(x))n＞0}.

注?x∈L,x∈D(L;σ)當且僅當ord(σ(x))=∞.

引理4.6設(L;σ)為態(tài)R0代數(shù),F是(L;σ)的真態(tài)濾子,則F?D(L;σ).

證任意x∈F,有σ(x)∈F,則對任意的n≥1,(σ(x))n∈F,又0/∈F,所以(σ(x))n/0即x∈D(L;σ).所以,F?D(L;σ).

引理4.7設(L;σ)為態(tài)R0代數(shù),則下列結論等價.

(1)D(L;σ)是 (L;σ)的態(tài)濾子.

(2)對任意x,y∈L和n≥1,由(σ(x))n,(σ(y))n0能推出(σ(x?y))n/0.

證(1)?(2)任意x,y∈L,對任意的n≥1,若(σ(x))n,(σ(y))n0即x,y∈D(L;σ),則x?y∈D(L;σ).所以(σ(x?y))n0.

(2)?(1)顯然1∈D(L;σ).設x,x→y∈D(L;σ),則對任意n≥ 1,有(σ(x))n,(σ(x→y))n＞0,由(2)可知[σ(x?(x→y))]n＞0.由于y≥x?(x→y),即σ(y)≥σ(x?(x→y)),所以(σ(y))n≥ [σ(x?(x→y))]n＞0.因此y∈D(L;σ)即D(L;σ)為濾子.設任意x∈D(L;σ)則對任意n≥1,有

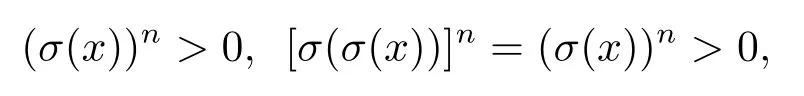
所以σ(x)∈D(L;σ).因此D(L;σ)為態(tài)濾子.

定理4.8設(L;σ)為態(tài)R0代數(shù),則下列條件等價.

(1)D(L;σ)是態(tài)濾子;

(2)〈D(L;σ)〉σ是真態(tài)濾子;

(3)D(L;σ)是(L;σ)的唯一極大態(tài)濾子;

(4)(L;σ)是態(tài)局部的.

證(1)?(2)顯然〈D(L;σ)〉σ=D(L;σ).由于0(L;σ),故〈D(L;σ)〉σ是真態(tài)濾子.

(2)?(3) 設〈D(L;σ)〉σ是真態(tài)濾子,由引理 4.6 知〈D(L;σ)〉σ?D(L;σ),又D(L;σ)?〈D(L;σ)〉σ,因此〈D(L;σ)〉σ=D(L;σ) 即D(L;σ) 為真態(tài)濾子. 假設F為 (L;σ) 的極大態(tài)濾子,即F?D(L;σ),由F的極大性知F=D(L;σ).因此D(L;σ)是(L;σ)的唯一極大態(tài)濾子.

(3)?(4)顯然.

(4)?(1)設F為(L;σ)的唯一極大態(tài)濾子.設x∈D(L;σ),則〈x〉σ是真態(tài)濾子,〈x〉σ可以延拓為極大態(tài)濾子Fx,由唯一性知Fx=F,因此x∈F,所以D(L;σ)?F.又F?D(L;σ),故D(L;σ)=F.因此D(L;σ)為態(tài)濾子.

定理4.9設(L;σ)為態(tài)R0代數(shù),(L;σ)是態(tài)局部的充要條件是對任意的x∈L,

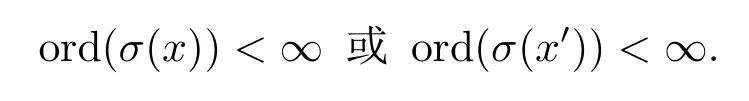
證?設(L;σ)是態(tài)局部,由定理4.8知,D(L;σ)是態(tài)濾子.假設存在x∈L使得對任意n≥ 1,(σ(x))n＞0 且(σ(x′))n＞0,由引理4.7,(σ(x?x′))n＞0,而x?x′=0,(σ(x?x′))n=0矛盾.所以,任意的x∈L,

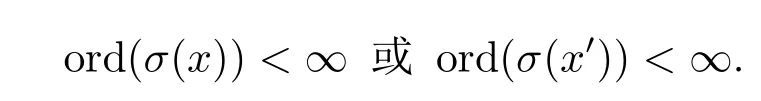
?顯然 1∈D(L;σ). 設x,x→y∈D(L;σ),則有 (x?y′)′=x→y∈D(L;σ)即 ord(σ(x?y′)′)=∞, 由條件可得 ord(σ(x?y′))＜∞. 設 ord(σ(x?y′))=m1, 即(σ(x?y′))m1=0,又

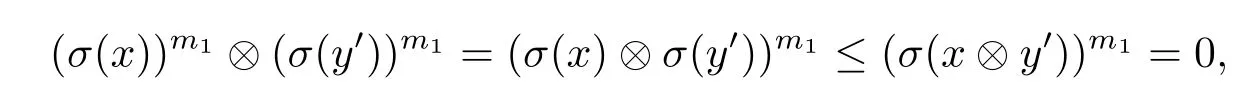
因此 (σ(y′))m1≤[(σ(x))m1]′.x∈D(L;σ), 即對任意n≥ 1,(σ(x))n＞0, 從而對任意m＞1,[(σ(x))m1]m＞0,即 ord(σ(x))m1=∞,所以 ord[(σ(x))m1]′=m2＜∞,即[((σ(x))m1)′]m2=0,因此

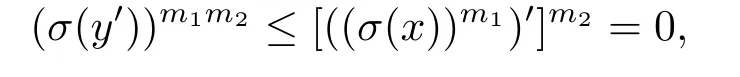
有 (σ(y′))m1m2=0,ord(σ(y′))＜∞,所以 ord(σ(y))=∞,即y∈D(L;σ). 設x∈D(L;σ),即 (σ(x))n＞0,(σ(σ(x)))n=(σ(x))n＞0,則σ(x)∈D(L;σ). 因此D(L;σ)為態(tài)濾子,由定理4.9知,(L;σ)是態(tài)局部的.

引理4.10設(L;σ)為態(tài)R0代數(shù),F是(L;σ)的態(tài)濾子,σ′：L/F→L/F上的映射且σ′(x/F)=σ(x)/F,則 (L/F;σ′) 為態(tài)R0代數(shù).

證由推論2.6可知L/F為R0代數(shù).又σ′(0/F)=σ(0)/F=0/F,當x→y=1時,

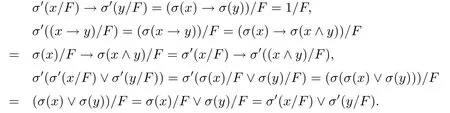
因此由定義3.1可知σ′為L/F上的態(tài)算子,所以(L/F;σ′)為態(tài)R0代數(shù).

定理4.11設(L;σ)為態(tài)R0代數(shù),F是(L;σ)的態(tài)濾子,則以下條件是等價的.

(1)(L/F;σ′)是態(tài)局部R0代數(shù),

(2)若對任意x,y∈L,x?y′∈F,則存在正整數(shù)n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

證(1)?(2)設(L/F;σ′)為態(tài)局部R0代數(shù)且x?y′∈F,即y→x′∈F,因此

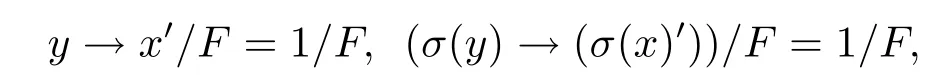
即σ(y)/F≤(σ(x))/F.假設對任意n≥1有((σ(x))n)′/∈F,(σ(x))n)′/F/=1/F,即(σ(x))n/F/=0/F,由定理4.9,ord(σ′(x′/F))＜∞,即存在m≥ 1 使得

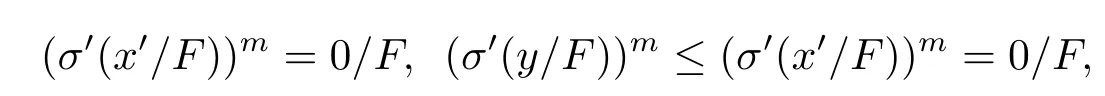
即 (σ(y))m/F=0/F,所以 ((σ(y))m)′/F=1/F,即 ((σ(y))m)′∈F.

(2)?(1) 由于(x?x′)′=1∈F,故存在n≥ 1 使得 ((σ(x))n)′∈F或 ((σ(x′))n)′∈F,即σ(x)n/F=(σ′(x/F))n=0/F或 (σ′(x′/F))n=0/F. 由定理 4.9 知 (L/F;σ′) 為態(tài)局部R0代數(shù).

定理4.12設(L;σ)為態(tài)R0代數(shù),F為(L;σ)的一個態(tài)濾子,則以下條件等價.

(1)(L;σ)為態(tài)局部的,

(2)對任意x,y∈L,若x?y′∈F,則存在正整數(shù)n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

證(1)?(2) 設(L;σ)為態(tài)局部的且F為(L;σ)的真態(tài)濾子.由引理4.6知,F?D(L;σ).由定理4.8知,D(L;σ)為態(tài)濾子.若x?y′∈F?D(L;σ),則對任意n≥ 1,(σ(x?y)′)n＞0即ord(σ(x?y))＜∞,因此存在n≥ 1使得(σ(x?y))n=0,即(σ(x))n=0 或 (σ(y))n=0,從而 ((σ(x))n)′=1∈F或 ((σ(y))n)′=1∈F.

(2)?(1)注意到{ 1}是(L;σ)的態(tài)濾子,σ′為上述所定義的映射,由定理4.10知(L/{1};σ′) 為態(tài)局部R0代數(shù). 又 (L;σ)(L/{1};σ′),所以 (L;σ)為態(tài)局部R0代數(shù).

由定理4.11和定理4.12,有以下推論.

推論4.13設(L;σ)為態(tài)R0代數(shù),F是(L;σ)的態(tài)濾子,σ′：L/F→L/F上的映射且σ′(x/F)=σ(x)/F,則以下條件是等價的.

(1)(L;σ)為態(tài)局部的,

(2)(L/F;σ′)是態(tài)局部R0代數(shù),

(3)對任意x,y∈L,若x?y′∈F,則存在正整數(shù)n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

[1]王國俊.模糊命題演算的一種形式演繹系統(tǒng)[J].科學通報,1997,42(10)：1041-1045.

[2]Wang G J.Non-classcal mathematical logic and approximate reasoning[M].Beijing：Science Press,2000.

[3]馬學玲,詹建明.模糊參數(shù)模糊軟R0代數(shù)[J].模糊系統(tǒng)與數(shù)學,2013,25-29.

[4]Ma X L,Zhan J M,Xu Y.Generalized fuzzy filters ofR0algebras[J].Soft Comput.,2007,1079-1087.

[5]李志偉,李桂華.模糊蘊涵代數(shù)的結構特征[J].數(shù)學雜志,2008,28(6)：701-705.

[6]Mundici D.Averaging the truth-value in Lukasiewicz logic[J].Studia Logica,1995,55(1)：113-127.

[7]Flaminio T,Montagna F.An algebraic approach to state on MV-algebras[J].Fuzzy Logic,2007：201-206.

[8]Ciungu L C,Dvurecenskij A.State BL-algebras[J].Soft Comput.,2011,15：619-634.

[9]裴道武,王國俊.形式系統(tǒng)￡?的完備性及其應用[J].中國科學(E輯),2002,32(1)：56-64.

[10]裴道武.R0代數(shù)的MP濾子與同余關系[J].模糊系統(tǒng)與數(shù)學,2002,16(專輯)：2002,16：22-25.

[11]張家錄.R0代數(shù)上的MP濾子格[J].模糊系統(tǒng)與數(shù)學,2006：26-33.

[12]劉練珍,李開泰.局部R0代數(shù)[J].數(shù)學研究與評論,2005：538-542.

[13]He P F,Xin X L.On state residuated lattices[J].Soft Comput.,2015,19(8)：1-12.

[14]Liu L Z,Zhang X Y.State onR0-algebras[J].Soft Comput.,2008,12：1099-1104.

ON STATER0-ALGEBRAS

QIN Yu-jing1,XIN Xiao-long1,HE Peng-fei2
(1.School of Mathematics,Northwest University,Xi’an 710127,China)(2.School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China)

In this paper,we study the problems of state operators.By using the method of introducing internal states on MV-algebras,we introduce the state operators onR0-algebras and define the stateR0-algebras,which are generalization ofR0-algebras.We give some non-trivial examples of stateR0-algebras and study some basic properties of them.Based on the above arguments we define the state filters and state localR0-algebras.We characterise the state localR0-algebras by the state filters,which generalizes the theory of localR0-algebras.

R0-algebra;stateR0-algebra;state fi lter;state local

on：06F25

O141.1

A

0255-7797(2017)04-0881-08

2015-07-09接收日期：2016-01-06

國家自然科學基金資助(11571281).

秦玉靜(1991-),女,河南焦作,碩士,主要研究方向：邏輯代數(shù).