Hom-弱Hopf代數(shù)上的Hom-smash積

鄭乃峰

(寧波大學(xué)理學(xué)院,浙江寧波 315211)

Hom-弱Hopf代數(shù)上的Hom-smash積

鄭乃峰

(寧波大學(xué)理學(xué)院,浙江寧波 315211)

本文研究了在Hom-Hopf代數(shù)上引入Hom-弱Hop代數(shù)的問題.通過建立弱左H-模Hom-代數(shù)的方法,構(gòu)造Hom-smash積,證明Hom-smash積是Hom-代數(shù),且給出使之成為Hom-弱Hopf代數(shù)的充分條件,推廣了由Bohm等人定義的弱Hop代數(shù).

Hom-弱Hopf代數(shù);弱左H-模Hom-代數(shù);Hom-smash積

1 引言

代數(shù)形變理論現(xiàn)在已是代數(shù)學(xué)的重要分支之一.近年來作為代數(shù)另一類形變代數(shù)-Hom-代數(shù)的引入,引起了許多代數(shù)學(xué)者的關(guān)注.Hom-代數(shù)的概念是由Makhlouf和Silvestrov于2006年在研究擬李代數(shù)時引入的(見文獻(xiàn)[1]).Hom-代數(shù)的引入實際上是推廣了結(jié)合代數(shù)的概念,把結(jié)合代數(shù)中的結(jié)合性法則作了形變,將其變成了線性變換α結(jié)合性條件,即α(a)(bc)=(ab)α(c).隨著Hom-代數(shù)研究的深入,一些學(xué)者在文獻(xiàn)[2-5]中又陸續(xù)引入了Hom-余結(jié)合余代數(shù)、Hom-雙代數(shù)和Hom-Hopf代數(shù)等,并給出了一些重要的性質(zhì).在文獻(xiàn)[6,7]中,作者定義了Hom-ω-smash積和Hom-ω-smash余積,并分別研究了它們的擬三角結(jié)構(gòu)和辮化結(jié)構(gòu).

弱Hopf代數(shù)是由Bohm 和Nill等人定義的(見文[8]),作為Hopf代數(shù)(見文[9])的推廣,弱Hopf代數(shù)與Hopf代數(shù)有著相似的構(gòu)成,只是用更弱的條件去代替余乘法運算的保單位性和余單位運算的保乘法性.因此,弱Hopf代數(shù)的結(jié)構(gòu)遠(yuǎn)比Hopf代數(shù)復(fù)雜.

綜合上述討論,在弱Hopf代數(shù)上引入Hom-代數(shù)的結(jié)合性條件成為自然的問題,這也是寫這篇文章的動機(jī).在Hom-弱Hopf代數(shù)和模結(jié)構(gòu)的基礎(chǔ)上,建立弱左H-模Hom-代數(shù)的結(jié)構(gòu)并通過它構(gòu)造Hom-smash積,證明Hom-smash積是Hom-代數(shù),且給出使之成為Hom-弱Hopf代數(shù)的充分條件.

2 Hom-弱Hopf代數(shù)

本文的所有工作都在域k上進(jìn)行的.所討論的張量積和線性映射均指域k上的.文中將使用Sweedler關(guān)于余代數(shù)余乘法的記號,即對于H中的任意元關(guān)于Hom-代數(shù)和Hom-余代數(shù)的概念請參閱文獻(xiàn)[1-3].

定義 2.1[10]如果(H,μ,η,α)是一個Hom-代數(shù),(H,△,ε,α)是一個Hom-余代數(shù),且代數(shù)和余代數(shù)結(jié)構(gòu)滿足下列相容性

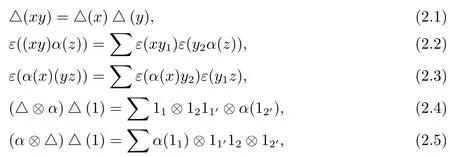
則稱六元組 (H,μ,η,△,ε,α)為一個 Hom-弱雙代數(shù),并簡記為 (H,α).

定義2.2[10]設(shè)(H,α)是一個Hom-弱雙代數(shù),S：H→H是一個線性映射,如果滿足

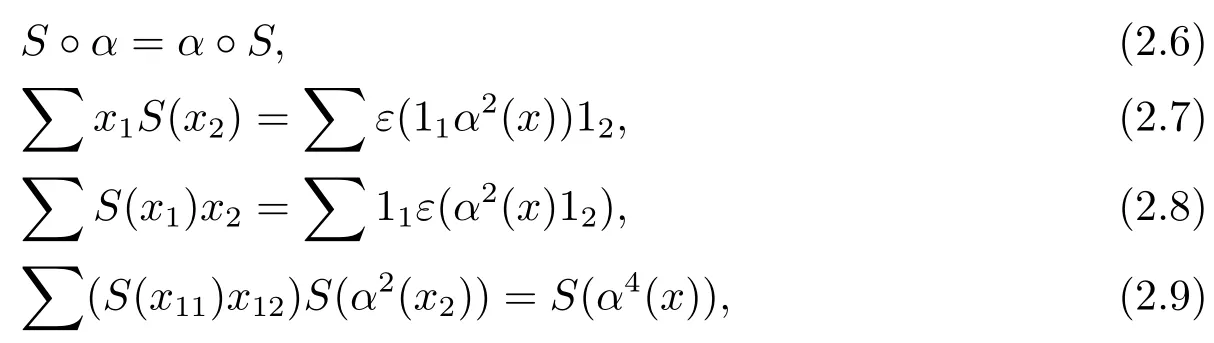
則稱(H,α)是一個Hom-弱Hopf代數(shù),并稱S是Hom-弱Hopf代數(shù)(H,α)的對極映射.

注2.3由(2.7)和(2.8)式,容易得到∑(x11S(x12))α2(x2)=α4(x)和∑α2(x1)(S(x21)x22)=α4(x).對于(2.9)式的合理性證明如下

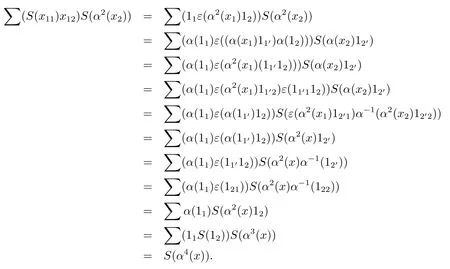
注2.4Hom-弱Hopf代數(shù)既不滿足結(jié)合律也不滿足余結(jié)合律,但當(dāng)扭曲映射α=Id時,它就是弱Hopf代數(shù).但當(dāng)余單位ε是代數(shù)映射時,Hom-弱Hopf代數(shù)就是Hom-Hopf代數(shù).相對于(余)結(jié)合性,Hom-弱Hopf代數(shù)也有Hom-(余)結(jié)合性,即μ?(α?μ)=μ?(μ?α)和(α?△)?△=(△?α)?△.因此Hom-弱Hopf代數(shù)的非(余)結(jié)合性的程度是由扭曲映射α偏離恒等映射的距離決定的.關(guān)于Hom-弱Hopf代數(shù)的相關(guān)性質(zhì)請參閱文獻(xiàn)[10].

命題2.5設(shè)(H,α)是一個Hom-弱Hopf代數(shù),且滿足條件ε?S=ε,則有如下結(jié)論

證對任意x∈H,有

同理可證=成立.

上面的命題說明S(HL)?HR和S(HR)?HL.由于α(1)=1,因此有∑α(11)?α(12)=∑11?12,所以有α(HL)?HL和α(HR)?HR.

命題2.6設(shè)(H,α)是一個Hom-弱Hopf代數(shù),則有如下結(jié)論

證對任意x,y∈H,有

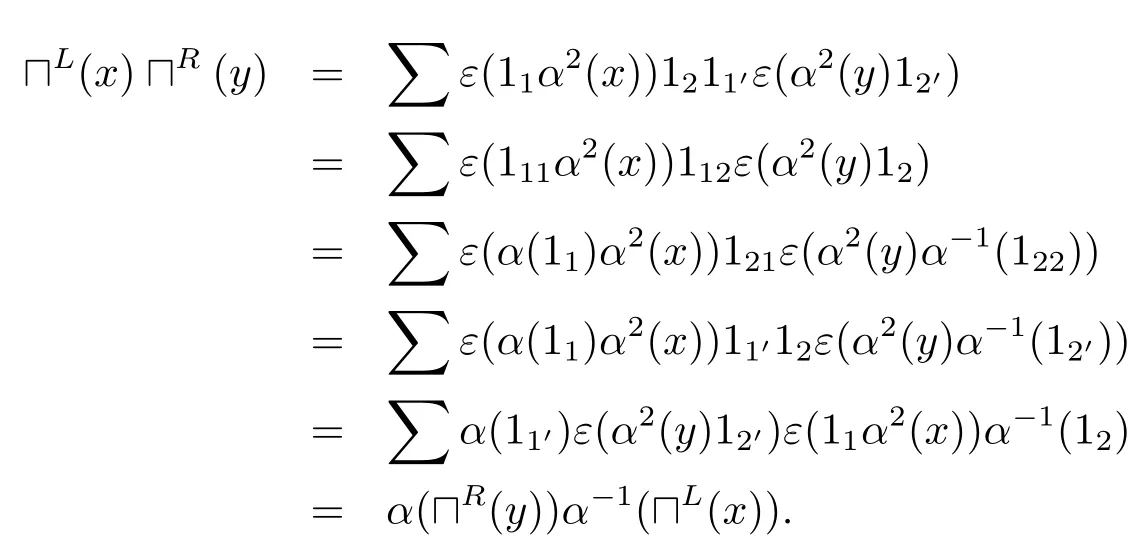
3 Hom-弱Hopf代數(shù)上的smash積

關(guān)于Hom-模、Hom-余模、Hom-模代數(shù)和Hom-模余代數(shù)的相關(guān)概念可參閱文獻(xiàn)[5].下面,給出弱左H-模Hom-代數(shù)的概念.

定義3.1設(shè)(H,α)是Hom-弱Hopf代數(shù),(A,β)是Hom-代數(shù).如果有一個線性映射ρ：H?A→A,ρ(h?a)=h·a,使得對任意h,g∈H和a,b∈A,有下面條件成立

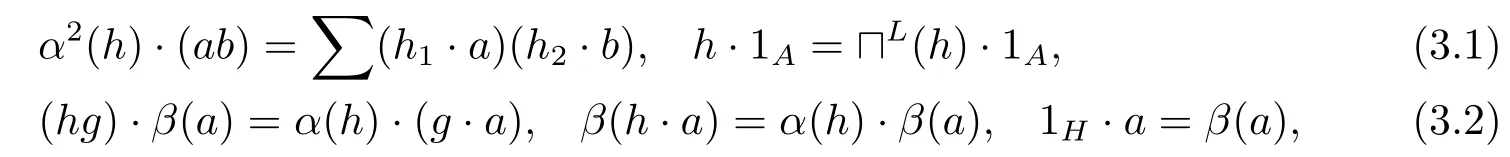
則稱Hom-代數(shù)(A,β)是一個弱左H-模Hom-代數(shù).若α=Id和β=Id,則弱左H-模Hom-代數(shù)是文獻(xiàn)[11]中的一個弱左H-模代數(shù).若(H,α)是Hom-Hopf代數(shù),則弱左H-模Hom-代數(shù)是文獻(xiàn)[5]中的一個左H-模Hom-代數(shù).

本節(jié)設(shè)(H,α)是Hom-弱Hopf代數(shù),其弱對極S是雙射,(A,β)是弱左H-模Hom-代數(shù),設(shè)=β?α.為方便,分別記1H為1,1A為.

(A,β)在(H,α)上的Hom-smash積(A#H,γ)是指帶有下面乘法運算的向量空間A?HLH,運算規(guī)定如下

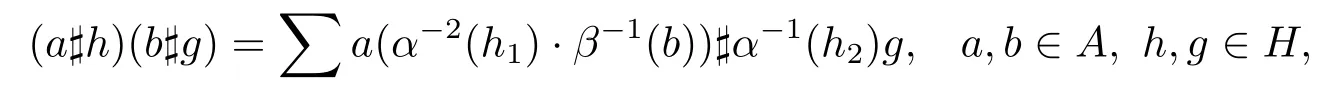
H通過乘法構(gòu)成左HL模,A通過下面作用構(gòu)成右H-模

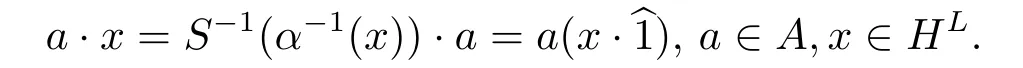
引理3.2(A,β)在(H,α)上的Hom-smash積是一個帶有單位元的Hom-代數(shù).

證 對任意a,b,c∈A和h,g,k∈H,有

注3.3若α=Id和β=Id,則Hom-smash積是文獻(xiàn)[12]中的smash積;若(H,α)是Hom-Hopf代數(shù),則Hom-smash積是文獻(xiàn)[6]中的Hom-smash積.

引理3.4設(shè)是一個Hom-smash積,則對任意a,b∈A和h,g∈H,下面關(guān)系式成立

證對任意a,b∈A和h,g∈H,有

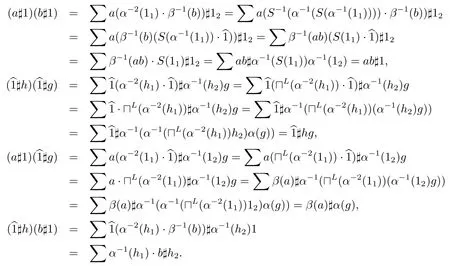
定理3.5設(shè)(H,α)是Hom-弱Hopf代數(shù),其弱對極為S,(A,β)是Hom-弱雙代數(shù).如果(A,β)是弱左H-模Hom-代數(shù),并且對于任意h∈H,a∈A,下面條件成立

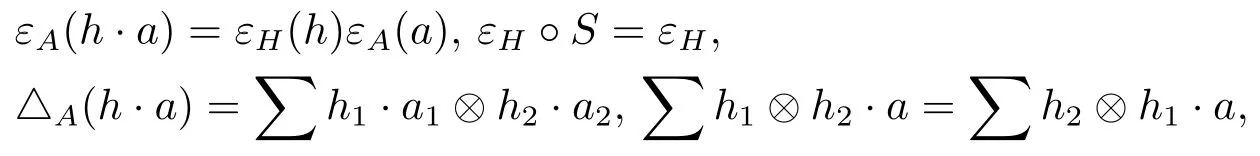
若此時(A,β)又是Hom-弱Hopf代數(shù),其弱對極為SA,滿足性質(zhì),則Hom-smash積也是Hom-弱Hopf代數(shù),其弱對極為

證顯然,Hom-smash積是Hom-代數(shù)和Hom-余代數(shù).假設(shè)定理條件成立,證明Hom-smash積滿足定義2.1的(2.1)-(2.5)項.對任意a,b∈A和h,g∈H,有

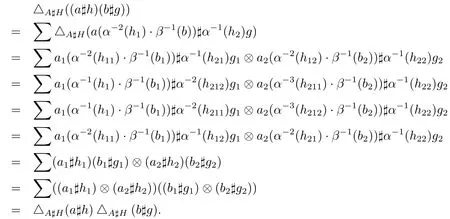
運用定理中的條件,可得如下關(guān)于余單位的弱乘運算

同理可得

由于對于任意的a∈A,x∈HL,有,因此有,又由于εH?S=εH成立,因此由命題 2.5 可知S(HL)?HR和S(HR)?HL成立,所以有

同理可得

最后,設(shè)(H,α)和 (A,β)是Hom-弱 Hopf代數(shù)且由于

對于定義2.2中的(2.9)式,利用定義3.1中的(3.1)、(3.2)式和引理3.3及定理中的條件,有

注3.6如果線性映射α和β是恒等映射,即對任意的a∈A和h∈H,有γ(a?h)=a?h,則Hom-smash積是由文獻(xiàn)[8]定義的弱Hopf代數(shù),并可得文獻(xiàn)[13]中的例1.8或文獻(xiàn)[16]中的定理2.2.如果(H,α)和(A,β)是Hom-Hopf代數(shù),則Hom-smash積是Hom-Hopf代數(shù),并可得文獻(xiàn)[6]中的例2.2.

[1]Makhlouf A,Silvestrov S.Hom-algebras structures[J].J.Gen.Lie Theory Appl.,2008,2：51-64.

[2]Caenepeel S,Goyvaerts I.Monoidal Hom-Hopf algebras[J].Comm.Alg.,2011,39(6)：2216-2240.

[3]Makhlouf A,Silvestrov S.Hom-algebras and Hom-coalgebras[J].J.Alg.Appl.,2010,9：553-589.

[4]Makhlouf A,Silvestrov S.Hom-Lie admissible Hom-coalgebras and Hom-Hopf algebras[A].Silvestrov S,Paal E,Abramov V,Stolin A,eds.Generalized lie theory in mathematics,physics and beyond[C].Berlin：Springer-Verlag,2009,189-206.

[5]Yau D.Hom-bialgebras and comodule Hom-algebras[J].Inter.Elect.J.Algebra,2010,8：45-64.

[6]鄭乃峰.Hom-ω-smash積Hopf代數(shù)的擬三角結(jié)構(gòu)[J].數(shù)學(xué)年刊,2013,34(6)：689-708.

[7]鄭乃峰.Hom-ω-smash余積Hopf代數(shù)上的辮化結(jié)構(gòu)[J].數(shù)學(xué)物理學(xué)報,2013,33(6)：1068-1088.

[8]Bohm G,Nill F,Szlachanyi K.Weak Hopf algebras I：Integral theory andC?-structure[J].J.Alg.,1999,221：385-438.

[9]Sweedler M.Hopf algebra[M].New York：Benjamin,1969.

[10]鄭乃峰.Hom-弱Hopf代數(shù)上的Hom-Smash余積[J].數(shù)學(xué)雜志,2016,36(2)：393-402.

[11]Nikshych D,Vainerman L.Finite quantum groupoid and their applications[J].Math.Sci.Res.Inst.Publ.,2002,43：211-262.

[12]Nikshych D.A duality theorem for quantum groupoids[J].Contemp.Math.,2000,267：237-243.

[13]鄭乃峰.弱Hopf代數(shù)上的Smash雙積[J].數(shù)學(xué)進(jìn)展,2009,38(5)：553-565.

[14]鄭乃峰.弱Hopf代數(shù)上的混合積[J].數(shù)學(xué)年刊,2010,31(6)：757-768.

[15]鄭乃峰.弱Hopf代數(shù)上的ω-交叉積[J].數(shù)學(xué)年刊,2012,33(1)：77-90.

[16]侯波,王志璽.弱Hopf代數(shù)作用與沖積[J].數(shù)學(xué)學(xué)報,2007,50A(1)：89-96.

HOM-SMASH PRODUCTS OVER HOM-WEAK HOPF ALGEBRAS

ZHENG Nai-feng
(College of Science,Ningbo University,Ningbo 315211,China)

In this paper,we study the concept of weak Hopf algebras over Hom-Hopf algebras. Using the method of establishing weak leftH-module Hom-algebras,we construct Hom-smash product and demonstrate that Hom-smash product is a Hom-algebra and Hom-weak Hopf algebra,which generalizes weak Hopf algebra introduced by Bohm etc..

Hom-weak Hopf algebra;weak leftH-module Hom-algebra;Hom-smash product

on：16W30;16E10

O153.3

A

0255-7797(2017)04-0871-10

2015-7-31接收日期：2015-11-25

國家自然科學(xué)基金資助(60873267);寧波自然科學(xué)基金資助(2011A610172).

鄭乃峰(1968-),男,浙江慈溪,副教授,主要研究方向：Hopf代數(shù)及量子群.