鋼筋混凝土塑性鉸的理解及應用
許肖卓


摘 要:鋼筋混凝土梁已經成為了混凝土房屋結構中必不可少的構件,為了鋼筋混凝土梁承載能力的充分發揮與利用,同時為了施工的方便與滿足質量要求,本文從塑性鉸的理解及應用的角度 ,著重闡述了塑性鉸的工作原理,詳細地分析了具體實例中塑性鉸在提高結構的極限承載能力方面的作用,有利于讀者深入認識、理解和應用塑性鉸。
關鍵詞:鋼筋混凝土梁;塑性鉸;超靜定結構;極限彎矩
1 鋼筋混凝土塑性鉸的理解
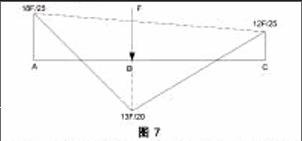
如圖1所示,當鋼筋混凝土梁受到集中荷載F的作用時,跨中截面內部的受拉鋼筋應力逐漸增大而達到屈服,在屈服階段應變持續增加而應力卻基本保持不變。混凝土受拉區裂縫不斷向受壓區發展,受壓區高度h0不斷減小,導致梁的曲率增加,當發展到一定程度時,受壓區的混凝土達到受壓極限強度,混凝土被壓碎而導致破壞。從這整個過程來看,由于鋼筋屈服階段的存在,梁的跨中截面形成了一個“鉸”,讓截面發生了很大的相對轉動,即圖2中的B點所示,我們稱這個 “鉸”為“塑性鉸”。對于普通鉸而言,塑性鉸的特點是能夠承受一定的彎矩,這是它們最本質的區別。
對于靜定結構而言,塑性鉸的出現只是結構延性破壞的一種體現,當靜定結構出現了塑性鉸之后,變成了機動體系,便不能再繼續承載,標志著結構達到破壞。但是,對于超靜定結構而言,當結構出現第一個塑性鉸之后,結構不會立即發生破壞,由于塑性鉸可以傳遞一定的彎矩使得結構可以繼續承載,只是減少了一個超靜定次數,整個結構的內力出現重分布,繼續加載,一直到下一個薄弱點出現塑性鉸,結構再一次減少一個超靜定次數,繼續加載,一直到結構最后變成機動體系,才算作最終破壞。超靜定結構中塑性鉸的存在讓結構承載力的提高以及控制破壞截面成為了可能。
但是,塑性鉸的產生必須要滿足一定的條件。塑性鉸的特性說到底是截面的轉動能力,可是卻要在一定的范圍內轉動,才能保持截面的穩定,以及彎矩的傳遞。條件的限制主要是體現在相對受壓區高度的大小上面,ξ是影響截面塑性轉動能力的主要因素,ξ值越小,則塑性鉸的轉動能力越大,故要求ξ≤0.35;同時如果截面配筋太小,會導致裂縫寬度太大,不能滿足正常使用的要求,所以還要求ξ≥0.1。在配有受壓鋼筋的雙筋截面中,要考慮受壓鋼筋的作用,因為受壓鋼筋能提高截面的塑性轉動能力。
2 超靜定結構中塑性鉸提高結構的承載力與控制破壞截面的原理
超靜定結構內的塑性鉸就像閘門,當結構承受外部荷載作用時,結構承載能力最薄弱的地方首先達到極限,打開閘門,將水疏導到承載能力高一級的大蓄水池當中,自身維持平衡、穩定。依次重復,最后最大的蓄水池也達到極限,整個結構最終遭到破壞。
如圖3所示,一端固定、一端鉸支的鋼筋混凝土梁,受到跨中集中荷載F作用。由結構力學知識我們可以求得此一次超靜定結構的各截面彎矩值大小(已經在圖3中標明),由于A截面所受的彎矩值大于C截面的彎矩值,在受到外荷載F作用時,A截面首先達到承載極限,受拉鋼筋達到屈服,截面上部混凝土開裂,梁會在A截面發生小幅度轉動,但是由于塑性鉸1(圖4)的形成,結構并不會立即失去承載能力,整個結構變成最簡單的簡支結構,并且結構的A端附加了A截面的極限彎矩Mu(具體數值由配筋決定)。
結構繼續承載,此時A截面所受到的彎矩的大小已經不會改變,已經達到A截面的承載能力最大值Mu,并且保持本身的平衡,增加的荷載由經過調幅到了C截面,當荷載值達到C截面的承載最大值時,鋼筋達到屈服,混凝土開裂,形成圖5中的塑性鉸2。最后結構變成機動體系,不能繼續承載。
從圖3各截面彎矩值可知,對于整個結構來說,A截面才是彎矩最大值的截面,也就是計算時的控制截面,但是由于塑性鉸的出現,將計算控制截面轉移到了C截面(跨中截面),并且可以通過控制C截面的極限彎矩Mu來達到提高整體結構承載極限的目的。
3 超靜定結構實例分析
兩端固定的鋼筋混凝土梁,bxh=200x400mm,采用C30混凝土(fc=14.3MPa,α1=1.0),HRB400鋼筋(fy=360MPa),配筋如下圖(單筋截面)。通過研究圖中鋼筋混凝土梁的集中極限荷載Fu,我們可以更加清楚地認識塑性鉸的作用。
當薄弱截面出現塑性鉸之后,截面還能承受彎矩值,即該截面的極限彎矩,所以第一步,我們必須求每個薄弱截面的極限彎矩Mu。
A截面:As=308mm2
X=(fyxAs)/(fcxbxα1)=(360x308)/(14.3x200x1.0)=38.77mm (0.1h0=36.5mm MuA=fyxAsx(h0-0.5X)=360x308x(365-0.5x38.77)=38.32kN.m 同理可得:B截面:As=402mm2 X=50.60mm MuA=49.16kN.m C截面:As=763mm2 X=96.04mm MuA=87.07kN.m 求得每個截面的極限彎矩之后,根據下圖所示彎矩圖,判斷截面出現塑性鉸的先后順序。 對于A、B、C三個截面來說, A截面所受彎矩是最大的,所以A截面才是控制截面,但是現在通過改變A、B、C截面的配筋,使得A截面所承受的彎矩值最早達到A截面的極限彎矩來改變整體結構的控制截面。 截面開始受力,A截面逐漸達到極限彎矩值38.32KN.m,形成第一個塑性鉸。此時,B、C截面所承受的彎矩值離極限彎矩值還差很多,還能繼續承載。F逐漸增大,B截面達到極限彎矩值49.16kN.m,再次形成一個塑性鉸,此時,A截面彎矩值保持38.32 KN.m 不變,C截面的彎矩值為66.57KN.m,依然未達到截面極限彎矩值。繼續加載,最后C截面達到極限彎矩87.07kN.m,截面徹底破壞。此時結構所承受的荷載即為極限荷載Fu。 可以通過以下簡單的計算求得Fu等于108.11KN,這個極限彎矩的值比未調幅之前同等配筋情況下的A截面極限彎矩值對應的Fu=53.22KN的2倍,可見塑性鉸具有很明顯的作用。 4 鋼筋混凝土梁塑性鉸在建設施工中的優點 通過彎矩調幅,可以將原本控制截面的支座處彎矩減少,調幅到跨中,人為地通過計算配筋來改變整體結構破壞的位置。這樣做還有以下優點: 減少梁支座處的配筋,增加跨中截面的配筋,有利于現場施工。支座處一般承受負彎矩,在截面上部配筋,但考慮到保護層的存在,實際施工并不好控制保護層厚度,但是跨中截面承受正彎矩,配筋在截面下方,有利于工人施工,并且質量也能得到保證。 在實際使用過程中,可以通過支座處或其他截面形成的塑性鉸來判斷結構的受力大小的情況,荷載過大時還能達到提前預警的效果。 梁的跨中截面便于及時的加固或修復。在跨中截面,承受正彎矩,可以在跨中截面底部通過粘貼鋼板加固的方法來施工作業,但是如果在支座處,破壞點位于截面上部,就需要通過錨固等方法來加固,然而錨固作業即不易操作也不經濟。 參考文獻 [1]上官子昌,經東風,王新明.混凝土結構設計原理[M].北京:機械工業出版社,2012. [2]樊友景,高洪波.結構力學(上冊)[M].鄭州:鄭州大學出版社,2012. [3]沈蒲生.混凝土結構設計原理(第四版)[M].北京:高等教育出版社,2013.

