利用函數思想巧解等差數列問題

張志鵬

數列是特殊的函數，而等差數列更是具備良好的函數性質，要是我們能夠利用好這些性質，不僅能夠使我們加深對數列的理解，更能使我們解決相應問題時更加得心應手.

一、等差數列中特定項的問題

我們假設數列{an}為等差數列，其公差為d，首項為a1.則易知其通項公式為an=a1+（n-1）dan=nd+（a1-d），若將an看成n的函數，我們會發現an是形如“kn+b”的關于n的線性函數，其中k等于公差d.既然是線性函數，我們知道其上任意的點都是“共線”的，利用這條性質我們便可以方便、高效地解決相應的類型問題.

例1已知數列{an}為等差數列，且a3=7，a15=31，則a17的值為.

常規解法由于{an}為等差數列，所以有a15=a1+14d；a3=a1+2d.求得首項a1=3，公差d=2，故a17=a1+16d=35.

巧妙解法由于{an}為等差數列，則易知（3，a3），（15，a15），（17，a17）三點共線，故其“斜率”相等，因而，我們得a15-a3115-3=a17-a15117-15，代入相應的值后我們解得a17=35.

點評：對于常規思路，要解決等差數列通項類的問題，我們一般需要轉換為首項a1和公差d來進行求解，需要兩個方程來解出這兩個參數，而我們從函數視角來解決此類問題時巧妙利用通項公式的函數特征，只需一步便可求得答案，無疑降低了計算量.

二、等差數列中前n項和的問題

設數列{an}為等差數列，其公差為d，首項為a1，則其前n項和sn=n（a1+an）12=d12n2+a1-d12n.若我們將sn看成n的函數，當公差d≠0時我們會發現sn是形如“an2+bn”的關于n的二次函數，并且其函數圖像過定點（0，0）.于是我們在解題時若能通過對二次函數圖像的解讀，并利用數形結合的思想來考慮問題，我們便可以快速找到相應的突破口.而函數g（n）=sn1n則是關于n的一次函數，既然是線性函數，我們知道其上任意的點都是“共線”的，利用這條性質我們也可以方便、高效地解決相應的類型問題.

例2已知等差數列{an}的前m項和為30，前2m項的和為100，求數列前5m項的和s5m的值.

常規解法由于{an}為等差數列，所以sm，s2m-sm，s3m-s2m，s4m-s3m，s5m-s4m仍為等差數列，故由題目可知sm，s2m-sm，s3m-s2m，s4m-s3m，s5m-s4m的值依次為30，70，110，150，190，所以s5m=30+70+110+150+190=550.

巧妙解法構造函數g（n）=sn1n，易知g（n）是關于n的一次函數.既然是線性函數，我們知道其上任意的點都是“共線”的，所以我們有：m，sm1m，2m，s2m12m，5m，s5m15m三點共線，因而，有s2m12m-sm1m12m-m=s5m15m-s2m12m15m-2m，代入解得s5m=550.

點評：常規解法利用了等差數列依次k項和仍為等差數列這一重要性質，但是當求和項太多時，例如，此題中求s100m，這類辦法便顯得不那么高明了，而我們創造性地構造g（n）=sn1n這一函數，利用其線性特征，便可以直接求出所需的前5m項之和，且此類方法不受求和項數量影響.

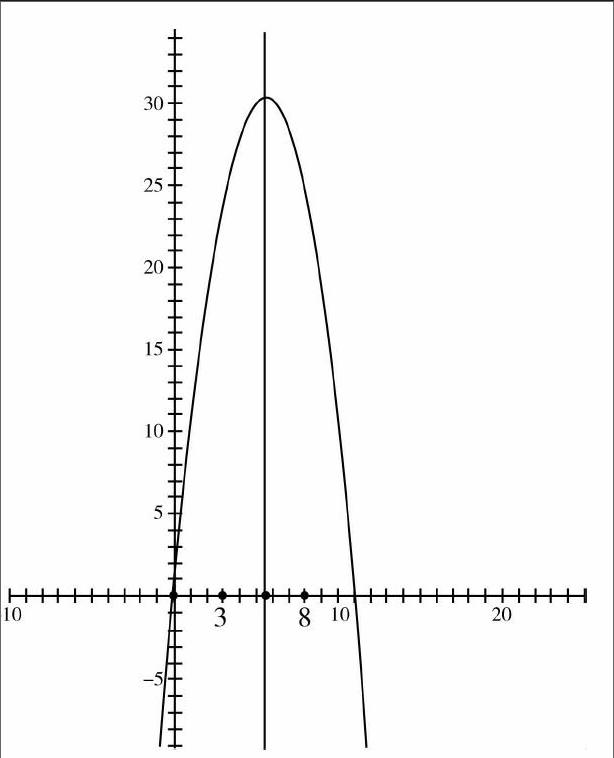
例3首項為正數的等差數列，前n項和為sn，并且s3=s8則當sn取得最大值時，n的值為.

常規解法由題可知公差d<0并有3a2=4（a4+a5），所以a2=-4d，故an=（n-6）d，所以a6=0.因此，前5項或者前6項的和最大，因此，答案為5或6.

巧妙解法由題可知s1=a1>0，并且公差d<0，因此，數列sn=d12n2+a1-d12n所對應的點所在函數的圖像如下圖所示.

由于s3=s8，所以對稱軸為n=3+812=5.5，又因為n為正整數且|5-5.5|=|6-5.5|，所以，前5項或者前6項的和相等，此時均取得最大值，因此，答案填5或6.

點評：題目直接告訴了我們sn中特定兩項的關系，而常規解法是將sn轉化為an來進行求解的，這不免走了一些彎路，而從函數視角出發，直接利用題目所給已知條件，抓住二次函數這一我們非常熟悉的函數的特征來解決問題，直奔主題，簡潔明了.