基于模糊神經網絡的光伏發電系統發電量的預測

徐新衛++滕翔++邵瑞瑞++丁敬安

[摘 要] 光伏系統的輸出電量由于受太陽日照量、氣候、光伏組件材料等多種因素影響而是一個非線性的變化量，因此對其輸出電量的準確預測可以提高光伏系統并網后電網的穩定性及安全性。在模擬實驗中，將模擬數據按春、夏、冬三季進行劃分從而確定了規則層的節點數為三，進而推導出模糊化層和去模糊化層的節點數，在訓練過程中通過梯度下降法來更新模糊神經網絡各層的參數，得到一個符合要求的預測網絡。將用于測試的數據輸入到訓練好的神經網絡中，用來驗證該方法的有效性。

[關鍵詞] 光伏系統；發電量預測；模糊神經網絡

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2017. 13. 077

[中圖分類號] TM615 [文獻標識碼] A [文章編號] 1673 - 0194（2017）13- 0180- 04

0 引 言

目前光伏發電量預測的方法主要有神經網絡法、灰色預測法、多元線性分析法這三種方法，通過對這三種預測模型進行比較，發現多元線性回歸和灰色理論雖然方法較為簡單，但是預測誤差也較大，而神經網絡法預測則可以比較準確但是預測過程較為繁雜。在基于神經網絡的預測中，多是以傳統的BP神經網絡為基礎模型，在此基礎上采用一些新的方法對BP網絡加以改進。例如在BP網絡的學習過程中采用Fletcher-Reeves共軛梯度算法，可以提高學習率，部分地簡化了預測過程，但輸入量過多，且預測的局限性較大。

在對比了眾多方法的優缺點之后，發現BP神經網絡普遍存在中間隱層數難以確定、輸入數據量過多，且學習時間過長等劣勢。因此本文提出了一種基于模糊神經網絡的預測模型，所選取的輸入量是和當天的發電量相關程度比較大的當天的平均氣溫以及當天的總日照量，模糊神經網絡的結構是由大量的先驗知識而設計出來的。在不影響預測精度的情況下，為了降低整個網絡的復雜程度，對整個網絡的模糊化層中的隸屬度函數及去模糊化層的輸出函數都做了適當的變化，解決了傳統神經網絡收斂速度慢的問題，從而使整個神經網絡結構簡潔，訓練速度較快，且預測精度較高。

1 模糊神經網絡

模糊神經網絡是在神經網絡和模糊系統的基礎上發展起來的，在模糊神經網絡出現之前，神經網絡與模糊系統都已有了多年的研究歷史，都有著較完備的理論基礎。

模糊神經網絡是一種將模糊邏輯推理的知識性結構和神經網絡的自學習能力結合起來的一種局部逼近網絡，融合彌補了神經網絡在數據處理方面的不足和模糊邏輯在學習方面的缺陷，是一個集語言計算、邏輯推理、分布式處理和非線性動力學過程為一身的系統。因此，它具有處理不確定信息的模糊推理能力和依據樣本數據進行學習的能力。模糊神經網絡主要利用神經網絡結構來實現模糊推理，從而使神經網絡的權值具有在模糊邏輯中推理參數的物理意義。

常見的模糊神經網絡有基于Mamdani推理的和基于Takgai-Sugeno推理的這兩種模糊神經網絡。基于Mamdani推理的模糊神經網絡多用于模糊邏輯控制器、模糊邏輯決策系統、模糊邏輯辨識系統等方面；基于Takgai-Sugeno推理的模糊神經網絡則是一種非線性模型，宜于表達復雜系統的動態特性。光伏系統的發電量由于受日照量、溫度、濕度、材料轉換率等多方面因素的影響，因此，光伏系統的輸出是一個不穩定的非線性變化的動態工程，所以本文所采用的就是基于Takgai-Sugeno推理的模糊神經網絡（簡稱TS模糊神經網絡）。

2 TS模糊神經網絡

2.1 TS模糊邏輯

在TS模糊邏輯系統中，模糊規則有著如下的特殊形式：

R（1）：if x1 is F1l，…，if xnis Fnl then

y l=P0l+P1lx1+…+Pnlxn

3 預測模型的建立

3.1 輸入量的確定

光伏電池之所以能發電，是由于當陽光照射到半導體材料的太陽能電池板上時，光能被吸收在太陽能電池內，并且產生電子（-）和空穴（+），而負價的電子多向n型聚集，正價的空穴多向p型聚集，因此，將太陽能電池的正面和背面接上電極與燈泡等負荷連接，就能產生電流。因此，日照量是影響光伏發電發電量的重要因素之一，所以日照量應作為輸入量之一。此外光伏發電的發電量還受溫度、濕度、安裝角度、材料轉換率等眾多因素的影響，在這眾多因素中，溫度對光伏發電量的影響是較大的，因此將溫度作為另一個輸入量輸入到預測模型中。

本文的輸入量為日照量與溫度組成的一個2×1的列向量，因為本文所預測的是晴天一整日的發電量（單位kW·h/日），因此，日照量取一整日的日照量（單位kW·h/日），溫度取一整日的平均溫度（單位℃）。若輸入向量用x表示，一整天的日照量用h表示，溫度用t表示，則輸入量可表示為下面的形式：

x=[h，t]T

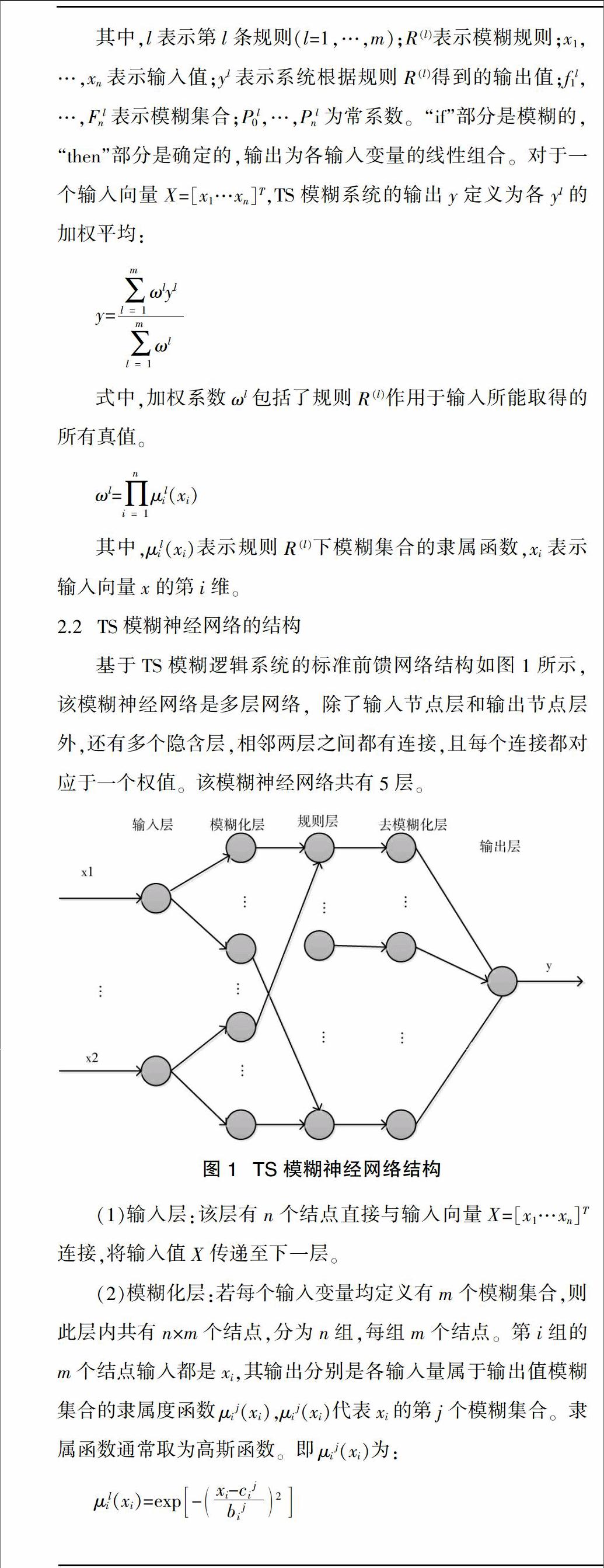
3.2 TS型模糊神經網絡結構與初始參數的確定

本文是針對全年晴天的當天發電量做出預測的，所以按季節劃分將全年的數據劃分成了春、夏、冬，由于秋天的日照量與溫度和春天的接近，所以在本文中并沒有單獨列出秋季，而是只按春、夏、冬三季的數據來建模預測。

由已有的先驗知識，可將數據按照春、夏、冬三季進行劃分，所以模糊神經網絡的規則層的隱層節點數也就為三，由于規則層已經確定，故可以知道模糊化層與去模糊化層的隱層節點數均為三個，因此可知本文的模糊神經網絡的預測模型結構如圖2所示。

3.3 TS型模糊神經網絡學習算法

設有輸入、輸出樣本為{（xl，dl），l=1，2，…，L}，在這里L表示訓練樣本的數量，為輸入向量，在本文中表示由當天日照量與當天平均溫度組成的一個2×1的列向量。將網絡誤差E設為：

E=■（yl-dl）2-||y-d|22

其中，y=[y1，y2，…，yL]T，表示神經網絡的實際輸出；d=[d1，d2，…dL]T，表示神經網絡的期望輸出；||.|2表示向量的2范數。

本文中，在不影響結果的前提下，為了降低神經網絡學習算法的復雜度，故將隸屬度函數變為：

ωij=exp-■（bij（xil-cij））2

將神經網絡的輸出函數變為：

yl =■ωij=（p0j+p1jx1l+…+pnjxnl）

因為本文是在MATLAB中進行編程預測，所以將各種數據都表示成矩陣的形式，通過對矩陣的處理，使模糊神經網絡的理解難度和操作難度都大大降低，因此，規定X=[x1，x2，…，xL]表示輸入樣本組成的n×L維矩陣；Ω=[ω1，ω2，…，ωL]表示輸入樣本X的隸屬度函數值ωl j所組成的m×L維矩陣；P=[p0，p1，…，pn]表示線性系數pi j所組成的m×（n+1）維矩陣；C=[c1，c2，…，cm]表示中心ci j所組成的n×m維矩陣；B=[b1，b2，…，bm]表示中心寬度bi j所組成的n×m維矩陣。

在訓練神經網絡時，首先計算隸屬度函數值ωl j所組成的矩陣Ω=[ω1，ω2，…，ωL]，在此基礎上計算神經網絡的輸出y及相應的誤差E；然后計算誤差E對系數矩陣P，B，C的偏導數，根據梯度下降法更新P，B，C；最后利用P，B，C來更新Ω，E等參數。如果未達到退出條件，則繼續迭代，達到了，則退出整個迭代過程，最終，就可以完成整個模糊神經網絡的訓練。在MATLAB中矩陣P和B的初始值可以由normrnd函數隨機生成，而矩陣C則可以由kmeans函數得到相應的初始聚類中心，通過訓練數據的學習過程，得到一個符合要求的模糊神經網絡。

4 預測模型的訓練與結果分析

為了使模糊神經網絡的訓練有較高的精度，需要大量的數據對模型進行評估訓練，本次模擬采用了120組數據進行預測，其中90組作為訓練樣本，30組作為測試樣本，所用的數據均是隨機模擬5kW光伏逆變器日發電量數據， 在訓練過程中，共取了90組數據來訓練，因此L=90；而規則數共有3條，因此這里m=3；而輸入的是有溫度與日照量組成的兩行一列的列向量，因此n=2；為了使訓練結果更加精確化，這里設置的最大迭代步數為1 000，迭代步長為0.001，圖3是訓練預測結果與實際結果的折線圖。

在圖中，實線表示預測輸出，用“+”表示實際輸出，而用虛線表示實際輸出與預測輸出之間的差值，從圖中可以明顯看出訓練好的模糊神經網絡符合要求。隨后，再將用于測試的數據帶入已訓練好的模糊神經網絡中，結果如圖4所示。

圖4是用于測試的數據的實際輸出與預測輸出的比較，“+”表示實際輸出，實線表示預測輸出，虛線表示實際輸出與預測輸出的差值。從預測的結果來看，相較于傳統的預測方法來說，本文所提出的模糊神經網絡的預測方法，不論是在預測精度上還是在訓練收斂速度上，都有一定程度的提高，雖說本文的原始數據并非實測數據，但是本文所用的數據皆是參考了大量資料之后擬合出的數據，所以有實際參考價值。

5 結 語

為了提高光伏并網系統的穩定性與安全性，本文提出了一種基于模糊神經網絡的電量預測模型。根據光伏系統的發電原理與大量的研究資料，確定了以每一天的日照量與平均溫度為整個系統的輸入量，來對這一整天的光伏系統的發電量做出預測，并且根據已有的先驗知識與相關理論，確定了本文所用的模糊神經網絡的結構。再通過擬合的符合實際的數據來訓練整個模型，最后通過一組測試數據來測試本預測模型是否達到要求。實驗結果表明，本模型能較為準確地預測出光伏發電系統一整天的發電量，具有一定的工程應用價值。

主要參考文獻

[1]李光明，廖華，李景天，等.并網光伏發電系統發電量預測方法的探討[J].云南師范大學學報：自然科學版，2011，31（2）：33-38.

[2]楊柳寧，孫以澤，孟婥，等.基于改進的BP神經網絡的光伏組件發電量預測模型設計[J].水電能源科學，2013，31（9）：243-246.