農產品供應鏈雙價值超網絡動態均衡分析

曹慧英+何亞輝+彭若愚+李昌兵

摘要：考慮經濟價值和信譽價值，構建由農產品生產商、分銷商和零售商構成的農產品供應鏈雙價值超網絡模型，利用變分不等式描述不同決策者的獨立行為以及決策者之間相互影響的競爭行為，確定供應鏈每層競爭成員達到均衡以及整個超網絡系統達到動態均衡的條件，在此基礎上，利用改進的投影梯度算法確定農產品交易中合理的冷鏈水平和交易量，以此促進物流在供應鏈成員間的有效性流動，降低整個供應鏈系統的不確定性，為提高整個農產品供應鏈網絡的利益均衡與長期穩定發展提供科學的分析依據。

關鍵詞：冷鏈水平；超網絡；變分不等式；雙價值；動態均衡

中圖分類號： F252.2文獻標志碼： A

文章編號：1002-1302（2017）10-0291-05

長期以來，我國的農產品在從生產者至消費者過程中，腐損率嚴重，果蔬產品的腐損率達到20%～30%，帶來的損失每年近4 807萬t，而發達國家農產品的腐損率卻低于5%，造成這種現象的主要原因是較低的農產品冷鏈流通率。目前，我國農產品的冷鏈流通率為10%左右，遠低于發達國家。2013年2月7日，國務院發布了《關于落實中共中央國務院關于加快發展現代農業進一步增強農村發展活力若干意見有關政策措施分工的通知》，其中，多項政策涉及農產品的冷鏈物流問題，這表示農產品供應鏈的冷鏈交易受到重視。與此同時，各個電商和傳統物流企業開始加速布局農產品的冷鏈物流，2013年，菜鳥物流牽手鄭明物流打造冷鏈物流平臺，順豐優選啟動華東華南冷鏈物流布局，京東冷鏈物流業也開始生鮮和農產品的冷鏈配送布局，故農產品供應鏈的冷鏈交易研究對我國農產品的安全效益和經濟效益具有重要的現實意義。

對于農產品供應鏈的冷鏈物流研究，冷志杰等建立了農產品供應鏈四維網絡模型，并對其進行了分析[1]。趙霞等利用混合粒子群算法來優化農產品網絡模型[2]。但斌等針對農產品供應鏈網絡的整鏈協調問題，考慮價值損耗條件下，集中決策是否有效的研究[3]。廖莉在農產品供應鏈分銷網絡中考慮了變質率、服務水平等因素，并對其進行了優化研究[4]。黃純輝則研究了食品冷鏈單鏈與跨鏈網絡的優化問題[5]。

以上大多研究農產品供應鏈企業的經濟價值，忽視了農產品交易中相對重要的信譽價值，有些電商物流企業甚至犧牲其前期的經濟利益而追求信譽價值最大化，以便占領市場實現最終盈利，對于鮮活度直接影響銷售水平和顧客滿意度、忠誠度的產品，企業的信譽價值更是其長期追求的目標。以上大部分研究也忽視了農產品供應鏈中各個企業的具體目標價值，更多的是從整鏈或者單個鏈點企業的利潤最大化來研究，而實際中各個企業都是追求其自身價值最大化。本研究首先選以超網絡模型來分析農產品供應鏈中各個企業追求的經濟價值和信譽價值最大化，構建了存在內在邏輯關聯的經濟價值網絡和信譽價值網絡，對各個企業進行2個網絡的分析，并給出最終的網絡均衡理論。

考慮冷鏈水平和合理的交易量對農產品供應鏈中各個企業總價值的影響，對于農產品供應鏈中的企業而言，冷鏈水平的提高一方面意味著其配送成本和固定成本的提高，針對城郊或城市內短途農產品配送，非冷鏈配送不會影響農產品的外觀，故不影響其交貨，但會影響農產品的保質期，另一方面，冷鏈水平的提高意味著產品高鮮活度帶來的信譽價值提高，合理的冷鏈水平和交易量是影響農產品供應鏈企業價值最大化的重要因素。

1雙價值超網絡模型的構建與供應鏈各成員行為分析

1.1超網絡簡介

美國學者Nagurney等提出，考慮供應鏈網絡中各層成員的各自行為與其他成員決策的相互影響，建立一個網絡均衡模型，第一次提出超網絡的概念[6]。超網絡作為一種可以有效解決多層次多目標且具有聯系的復雜系統的工具，在計算機[7]、組織知識分析[8]、價格決策[9]、電力[10]、生態[11]、運輸[12]等領域得到了廣泛應用。王眾托院士將超網絡概念引入中國，并指出了超網絡是具有多層性、多屬性、多準則的“高于而又超于現存網絡”的一種網絡[13]。浠玉虎等對超網絡的基本概念、特點和常見模型進行了總結和探討，給出了超網絡均衡的一般解法[14]。

1.2雙價值農產品供應鏈超網絡模型的構建

本研究構建的農產品供應鏈雙價值超網絡模型（圖1），由經濟價值網絡和信譽價值網絡組成，經濟價值網絡即實際農產品供應鏈帶來的經濟收益，與之相應是在農產品交易時所同時產生的信譽價值網絡；每個網絡都包括3層網絡結構，第一層代表生產商集合，第二層代表分銷商集合，第三層代表零售商集合，同層之間的虛線表示相關影響關系，是一種競合關系，各分層之間的實線代表非冷鏈運輸方式，虛線代表冷鏈運輸方式。

[FL（2K2]由于交易過程中的各個企業的交易是一個相互影響、相互交織的整體系統，上游企業和下游企業的交易量和冷鏈水平會繼續對下游企業與更下一級企業的交易造成影響。另一方面，對于理性的企業，經濟價值是其追求的目標，在面臨市場競爭時，又會注重其信譽的高低，即其信譽價值。考慮各層之間和各個企業價值之間的協調，應用超網絡能求得整體供應鏈的流量均衡和價值均衡的特征，構建超網絡模型，能保證整個供應鏈中各層企業之間交易量協調和冷鏈水平的協調。

模型滿足以下假設：H1：農產品在生產商分銷商零售商運輸時的成本（冷鏈或非冷鏈）均由上游企業承擔。H2：各個企業都是理性的，都追求其自身的經濟價值和信譽價值最大化。H3：農產品選擇非冷鏈運輸方式時，不會發生影響交貨的重大變質，僅僅在影響其鮮活度。H4：假設模型中農產品為同質產品。H5：各層之間為非合作競爭的關系。H6：信譽價值只考慮于交易雙方中的賣方，即在交易過程中買方處于較高地位。H7：相關成本函數和價值函數均為連續可微的凸函數。模型中的各個符號見表1。

1.3模型中各層企業雙重價值目標分析

1.3.1農產品供應鏈超網絡中各生產商的目標分析

生產商m在與分銷商n的農產品冷鏈配送交易中，其經濟收益為pmnqmn，經濟成本包括3部分，農產品的生產成本cm（qm）；冷鏈帶來的額外成本cmmn（lmn，qmn，rmn）（如冷鏈設施的購置成本、冷鏈配送中額外的油氣費用等），此成本與冷鏈水平lmn、交易量qmn、運輸距離rmn相關；與分銷商n的交易成本cmbmn（qmn，hmn）（如搬運裝卸費用、信息溝通費用、押金預付款等），此成本與交易量qmn、信譽度hmn有關。故其經濟價值最大化即為：

[JZ][HT6，6"]maxU1=∑[DD（]Nn=1[DD）]pmnqmn-cm（qm）-∑[DD（]Nn=1[DD）]cmmn（lmn，qmn，rmn）-∑[DD（]Nn=1[DD）]cmbmn（qmn，hmn）；

[JZ（]s.t. qm=∑[DD（]Nn=1[DD）]qmn，qmn≥0，0≤lmn≤1，rmn≥0，hmn≥0，pmn≥0。[JZ）][JY]（1）

在交易過程中其獲得的信譽價值與冷鏈水平、到貨時間（假設冷鏈與非冷鏈配送速度相同，故此項可變為運輸距離）、交易頻率有關。故其信譽價值最大化即為：

[JZ（][JB（]maxU2=∑[DD（]Nn=1[DD）]hmn（lmn，rmn，fmn）；

s.t. 0≤lmn≤1，rmn≥0，fmn≥0。[JB）][JZ）][JY]（2）

生產商的多目標雙價值最大化問題通常采取標準權函數來解決，本研究采用常數權重為1的標準權函數[15]，即企業認為在交易和配送過程中經濟價值和信譽價同等重要。故生產商的雙價值最大化決策為：

maxUm=U1+U2=∑[DD（]Nn=1[DD）]pmnqmn-cm（qm）-∑[DD（]Nn=1[DD）]cmmn（lmn，qmn，rmn）=∑[DD（]Nn=1[DD）]cmbmn（qmn，hmn）+∑[DD（]Nn=1[DD）]hmn（lmn，rmn，fmn）；

s.t. qm=∑[DD（]Nn=1[DD）]qmn，qmn≥0，0≤lmn≤1，rmn≥0，hmn≥0，pmn≥0，fmn≥0。[JY]（3）

根據假設H7，上式（3）為連續可微函數和變分不等式等價性，故公式（3）的解（q*mn，l*mn）等價于如下變分不等式的解：

∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]-pmn[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmmnlmn[SX）]+[SX（]cmmnlmn[SX）]-[SX（]hmnlmn[SX）][JB））]（lmn-l*mn）≥0。[JY]（4）

1.3.2農產品供應鏈超網絡中各分銷商的目標分析

分銷商n與零售商k交易過程中，其收益為pnkqnk，分銷商n的成本包括從生產商m處購買農產品的成本pmnqmn，與生產商m的交易成本cnbmn（qmn，hmn），與零售商z交易配送時的冷鏈成本cnnk（lnk，qnk，rnk），與零售商z的交易成本cnbnk（qnk，hnk）。故cnbnk（qnk，hnk）其經濟價值最大化即為：

maxV1=∑[DD（]Kk=1[DD）]pnkqnk-∑[DD（]Mm=1[DD）]pmnqmn-∑[DD（]Xm=1[DD）]cnbmn（qmn，hmn）-∑[DD（]Kk=1[DD）]cnnk（lnk，qnk，rnk）-∑[DD（]Kk=1[DD）]cnbnk（qnk，hnk）；

s.t. ∑[DD（]Mm=1[DD）]qmn≥∑[DD（]Kk=1[DD）]qnk，qmn≥0，qnk≥0，0≤lmn≤1，rnk≥0，hmn≥0，hnk≥0，pmn≥0，pnk≥0。[JY]（5）

在交易過程中其獲得的信譽價值為hnk，信譽度與農產品的鮮活度、到貨時間（假設冷鏈與非冷鏈配送速度相同，故此項可變為運輸距離）、交易頻率有關。故其信譽價值最大化即為：

[JZ（][JB（]maxV2=∑[DD（]Kk=1[DD）]hnk（lnk，rnk，fnk）；

s.t. 0≤lnk≤1，rnk≥0，fnk≥0。[JB）][JZ）][JY]（6）

分銷商的多目標雙價值最大化問題通常采取標準權函數來解決，采用常數權重為1的標準權函數[15]。故分銷商的雙價值最大化決策為：

maxVn=V1+V2=∑[DD（]Kk=1[DD）]pnkqnk-∑[DD（]Mm=1[DD）]pmnqmn-∑[DD（]Xm=1[DD）]cnbmn（qmn，hmn）-∑[DD（]Kk=1[DD）]cnnk（lnk，qnk，rnk）-∑[DD（]Kk=1[DD）]cnbnk（qnk，hnk）+∑[DD（]Kk=1[DD）]hnk（lnk，rnk，fnk）。[JY]（7）

根據假設H7，上式（7）為連續可微函數和變分不等式等價性，故公式（7）的解（q*mn，q*nk，l*mn，l*nk，β*）等價于如下變分不等式的解：

[JP4]∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（]pmn+[SX（]cnbmnqmn[SX）]-β[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]nn=1[DD）][JB（（][SX（]cnbmnlmn[SX）][JB））]（lmn-l*mn）+[JP3]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（]β-pnk+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）][JB））]（qnk-q*nk）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（][SX（]cnnklnk[SX）]+[SX（]cnbnklnk[SX）]-[SX（]hnklnk[SX）][JB））]（lnk-l*nk）+∑[DD（]Nn=1[DD）][JB（（]∑[DD（]Mm=1[DD）]qmn-∑[DD（]Kk=1[DD）]qnk[JB））]（β-β*）≥0。[JY]（8）

式中，β為拉格朗日乘子。

1.3.3農產品供應鏈超網絡中各零售商的目標分析

零售商是否決定從分銷商處購買農產品，取決于農產品的購買價格、其他成本和銷售價格，即下式成立[16]：

[JZ（]pnk+ckdete（lmn，lnk，qnk）[JB（{]=p*k，qnk>0≥p*k，qnk=0[JB）]。[JZ）][JY]（9）

[JZ（]d*k=[JB（{]=∑[DD（]Nn=1[DD）]q*nk，p*k>0≤∑[DD（]Nn=1[DD）]q*nk，p*k=0[JB）]。[JZ）][JY]（10）

公式（9）說明零售商從分銷商購買農產品的價格pnk，與單位變質成本ckdete（lmn，lnk，qnk）之和不能超過市場對產品的需求價格（即零售價格），此時零售商才會從分銷商處購買產品出售給零售市場上的需求者（其中單位變質成本與農產品到達零售商時的鮮活度有關，即與農產品從生產商到分銷商的冷鏈水平、從分銷商到零售商的冷鏈水平和交易數量有關）。公式（10）說明在均衡狀態下，如果零售市場中的消費者愿意購買此種農產品，則此時需求量恰好等于供給量，當供給大于需求時，市場中產品的價格為零。說明了農產品的零售市場為完全競爭市場，這與經濟學中對農產品市場的說明一致。

由變分不等式互補形式的等價性，可將零售商的決策條件公式（9）、公式（10）轉化為最優的（q*nk，p*k），即下式成立：

[HT6，6"][JZ（]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）]（pnk+ckdete-pk）（qnk-q*nk）+∑[DD（]Kk=1[DD）][JB（（]∑[DD（]Nn=1[DD）]qnk-dk[JB））]（pk-p*k）≥0。[JZ）][JY]（11）

2農產品供應鏈雙價值超網絡模型均衡分析

由以上分析可知，農產品供應鏈的雙價值超網絡模型的均衡狀態是存在唯一最優解（q*mn，l*mn，q*nk，l*nk，β*，p*k）滿足公式（4）、公式（8）、公式（11）3式之和，即下式：

∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]-pmn[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmmnlmn[SX）]+[SX（]cmbmnlmn[SX）]-[SX（]hmnlmn[SX）][JB））]（lmn-l*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（]pmn+[SX（]cnbmnqmn[SX）]-β[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cnbmnlmn[SX）][JB））]（lmn-l*mn）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（]β-pnk+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）][JB））]（qnk-q*nk）+[JP4]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（][SX（]cnnklnk[SX）]+[SX（]cmbnklnk[SX）]-[SX（]hnklnk[SX）][JB））]（lnk-l*nk）+∑[DD（]Nn=1[DD）][JB（（]∑[DD（]Mm=1[DD）]qm-∑[DD（]Kk=1[DD）]qnk[JB））]（β-β*）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）]（pnk+ckdete-pk）（qnk-q*nk）+∑[DD（]Kk=1[DD）][JB（（]∑[DD（]Nn=1[DD）]qnk-dk[JB））]（pk-p*k）≥0。[JY]（12）

證明：

必要性：將公式（4）、公式（8）、公式（11）3式相加即得到式（12）。

充分性：將證明必要性時消掉的項加入到式（12），得到公式（4）、公式（8）、公式（11）加總后的公式，再將其分開為公式（4）、公式（8）、公式（11）式即可。

從公式（12）中可以得到農產品雙價值超網絡模型整體均衡的條件，即在3層交易模型中，各個企業在尋求各自經濟價值和信譽價值最大化時，整體網絡能在合理的冷鏈水平和交易量時達到均衡穩定狀態，這時各個企業的雙價值都達到了盡可能的最大化，而且交易網絡也達到穩定的狀態。

在對公式（12）進行求解變分不等式時，梯度投影算法可以求解連續凸函數的變分不等式的解，由于假設的函數都是凸函數且是利普希茨連續的，故使用一種改進后的投影梯度算法來求解[17]。

此算法經過確定初值、計算、改進、收斂保證4個步驟后得到變分不等式的解為：

qTmn=max[JB（[]0，qT-1mn-θ[JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]+[SX（]cnbmnqmn[SX）]-βT-1n[JB））][JB）]]；

lTmn=min[JB（{]1，max[JB（[]0，lT-1mn-θ[JB（（][SX（]cmmnlmn[SX）]+[SX（]cmbmnlmn[SX）]-[SX（]hmnlmn[SX）]+[SX（]cnbmnlmn[SX）]）[JB））][JB）]][JB）}]；

qTnk=max[JB（[]0，qT-1nk-θ[JB（（]βT-1n+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）]+ckdete-pT-1k[JB））][JB）]]；

lTnk=max[JB（[]0，lT-1nk-θ[JB（（][SX（]cnnklnk[SX）]+[SX（]cnbnklnk[SX）]-[SX（]hnklnk[SX）][JB））][JB）]]；

pTK=max[0，pT-1k-θ（∑[DD（]Nn=1[DD）]qT-1nk-dk）]；

βTn=max[0，βT-1n-θ（∑[DD（]Mm=1[DD）]qT-1mn-∑[DD（]Kk=1[DD）]qT-1nk）]。

其中T為迭代次數。

3數值仿真案例

本研究選擇了上面的改進投影梯度算法來對超網絡模型所得的變分不等式來進行優化求解。為便于分析，將模型簡化，簡化生產商、分銷商和零售商個數都為2，即M=2、N=2、K=2。其余各個成本函數和交易函數為：

c1（q1）=2.1（q211+q212）-1 500（q11+q12），c2（q2）=2.1（q221+q222）-1 500（q21+q22）。

[JZ]hmn=2l2mn-0.1rmn+fmn，hnk=2l2nk-0.1rnk+fnk。

[JZ]cmbmn=0.3qmn-50hmn，cnbnk=0.3qnk-50hnk。

[JZ]cmmn=100lmn+0.1qmn，cnnk=100lnk+0.1qnk。

[JZ]dk=600-20pk。

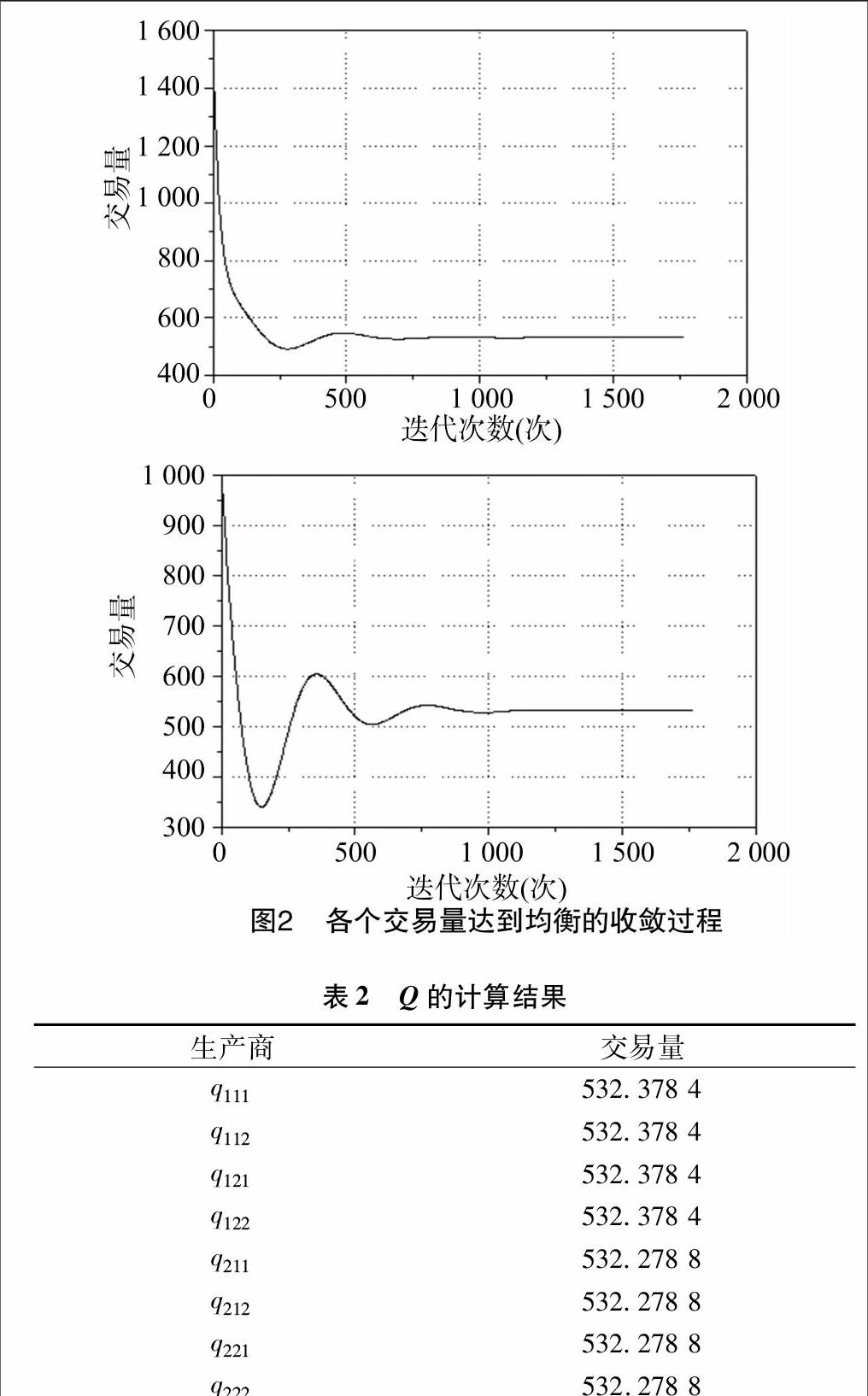
應用Matlab R2010b實現改進的投影梯度算法對模型進行求解，令收斂精度為0.001，將上面各函數求梯度帶入變分不等式的解可得均衡解。花費3 s，迭代1 763步實現收斂，從圖2可以看出，各個交易量隨著迭代次數的增大而逐步收斂到一個不動點，即模型中各層企業交易量在收斂到不動點時，各方的競合過程達到均衡，此時模型得到了均衡解。故此模型的均衡解為：lmn=lnk=1，p1=p2=3。在設計價值函數時，假設企業對其經濟價值和信譽同等看重，則其冷鏈水平均為1，即在企業認為經濟價值和信譽價值同等重要時，最優冷鏈水平為1。企業會盡可能提高自己的冷鏈配送水平，以達到經濟價值和信譽價值最大化。各企業間的均衡交易量見圖2（橫軸為迭代次數，縱軸為交易量）。

從圖2可以看出，超網絡各層交易量不斷振蕩直到達到均衡的過程，表明了交易量在本仿真試驗中可以逐漸收斂并達到最終穩定，證明了仿真試驗中各式的正確性和數據的合理性。

從表2可以看出，q111、q112、q121、q122分別代表2個生產商M=1，2與2個分銷商N=1，2的交易量，q211、q212、q221、q222分別代表2個分銷商N=1，2與2個零售商K=1，2的交易量。

供應鏈同層企業存在競合關系，各層企業的交易流量應該是基本相同的，從分析結果可以看出，生產商與分銷商的交易量和分銷商和零售商的交易量大致相同，證明了模型的正確和有效。各層企業的雙價值函數都包括經濟價值和信譽價

[值，且假設各個企業2個價值函數權重都相同，在這種情況下，冷鏈水平為1時，此模型達到均衡，證明在企業認為經濟價值和信譽價值同等重要的情況下，冷鏈水平達到1時，雙價值能達到最大。對于新興的冷鏈配送企業，當其認為信譽價值比經濟價值重要時，均衡的冷鏈水平和交易量即會發生變化。因此對于不同的企業，當其有不同的雙價值權重時，相應的均衡交易量和冷鏈水平也會隨之變化。

4結論

本研究構建了農產品供應鏈超網絡雙價值模型，探討了農產品冷鏈運輸物流網絡中各個企業在追求雙價值最大化時，整個供應鏈模型的動態均衡條件，并對模型進行了仿真試驗和數值分析。即構建了3層冷鏈網絡均衡模型，利用變分不等式求得各層企業各自雙價值最大化時的決策，并最終得到整個網絡模型均衡條件，隨后利用改進后的投影梯度算法對仿真模型進行求解分析。結果表明，合理的冷鏈水平和交易量能使整個農產品冷鏈物流配送網絡達到均衡狀態，給農產品冷鏈物流配送網絡中的各個企業和整體網絡的長期均衡發展提供了科學的分析方法和指導意義。

今后研究中，需要繼續優化模型使其與實際冷鏈配送情況更加一致，進一步放開假設條件和完善限制條件，并結合現實冷鏈配送情景，求出更符合現實的均衡條件，提供更好的決策建議。

參考文獻：

[1]冷志杰，唐煥文. 大宗農產品供應鏈思維網絡模型及應用[J]. 系統工程理論與實踐，2005，3（3）：39-45.

[2]趙霞，竇建平. 求解農產品供應鏈網絡設計問題的混合粒子群算法[J]. 管理工程學報，2013，27（4）：169-177.

[3]但斌，陳軍. 基于價值損耗的生鮮農產品供應鏈協調[J]. 中國管理科學，2008，16（5）：42-49.

[4]廖莉. 農產品供應鏈網絡模型及優化策略研究[D]. 濟南：山東大學，2011.

[5]黃純輝. 食品冷鏈物流運輸服務網絡優化研究[D]. 武漢：武漢理工大學，2012.

[6]Nagurney A，Dong J，Zhang D. A supply chain network equilibrium model[J]. Transportation Research Part E Logistics & Transportation Review，2002，38（5）：281-303.

[7]Low S H，Paganini F，Doyle J C.Internet congestion control[J]. IEEE Control Systems Magazine，2002，22（1）：28-43.

[8]席運江，黨延忠，廖開際. 組織知識系統的知識超網絡模型及應用[J]. 管理科學學報，2009，12（3）：12-20.

[9]Bautu E，Kim S，Bautu A，et al. Evolving hypernetwork models of binary time series for forecasting price movements on stock markets[C]. IEEE Congress on Evolutionary Computation，2009：166-173.

[10]Matsypural D，Nagurney A，Liu Z. Modeling of electric power supply network with fuel suppliers viavariational inequalities[J]. International Journal of Emerging Electric Power Systems，2007，8（1）：1-5.

[11]Sonntag M，Teichert H M. Competition hypergraphs[J]. Discrete Applied Mathematics，2004，143（1/2/3）：324-329.

[12]Emmerink R H M，Axhausen K W，Nijkamp P，et al. Effects of information in road transport networks with recurrent congestion[J]. Transportation，1995，22（1）：21-53.

[13]王眾托，王志平. 超網絡初探[J]. 管理學報，2008，5（1）：1-8.

[14]漆玉虎，郭進利. 超網絡研究[J]. 上海理工大學學報，2013，35（3）：227-239.

[15]Nagurney A，Ke K. Financial networks with electronic transactions：modelling，analysis and computations[J]. Quantitative Finance，2003，3（2）：71-87.

[16]Bertsekas D P，Tsitsiklis J N. Parallel and distributed computing[M]. New Jersey：Prentice-Hall，1989.

[17]Korpelevich G M. The extragradient method for finding saddle points and other problems[J]. Matecon，1976，12：747-756.