基于EMD-HMM的轉(zhuǎn)盤軸承故障診斷方法

孫炎平，陳捷，洪榮晶，封楊

（南京工業(yè)大學(xué) 機(jī)械與動(dòng)力工程學(xué)院，南京 210009）

作為核心回轉(zhuǎn)連接部件，轉(zhuǎn)盤軸承常用于工程機(jī)械、風(fēng)力發(fā)電、煤礦機(jī)械、港口機(jī)械、軍用裝備等領(lǐng)域［1］。與普通軸承相比，轉(zhuǎn)盤軸承的尺寸大（0.5～5 m）、轉(zhuǎn)速低（＜25 r／min）、承載工況復(fù)雜（需同時(shí)承受軸向力、徑向力和傾覆力矩）；而且工作環(huán)境惡劣，安裝、潤(rùn)滑及維修都非常不便；這就要求轉(zhuǎn)盤軸承運(yùn)行平穩(wěn)、安全、壽命長(zhǎng)，否則一旦發(fā)生故障將造成嚴(yán)重?fù)p失，因此對(duì)轉(zhuǎn)盤軸承進(jìn)行監(jiān)測(cè)和故障診斷意義重大。

近幾年，智能故障診斷方法得到了越來越多的應(yīng)用，但這些方法大多忽略了故障發(fā)生前后的連續(xù)性信息，僅僅停留在靜態(tài)觀測(cè)基礎(chǔ)上，比如通過對(duì)比分析某時(shí)刻的幅值譜來判斷是否發(fā)生故障，而忽略了故障變化發(fā)展的動(dòng)態(tài)信息。隱馬爾可夫模型（Hidden Markov Model，HMM）是一種時(shí)間序列的概率模型［2］，能夠有效描述隨機(jī)過程的統(tǒng)計(jì)特性，并對(duì)觀測(cè)序列進(jìn)行有效地模式識(shí)別和分類，挖掘出潛在的故障發(fā)生前后的上下文信息并加以利用，在機(jī)械設(shè)備狀態(tài)監(jiān)測(cè)和故障診斷領(lǐng)域引起了廣泛的關(guān)注［3-6］。

由于轉(zhuǎn)盤軸承轉(zhuǎn)速低，振動(dòng)信號(hào)微弱，故障特征難以提取，對(duì)大型轉(zhuǎn)盤軸承的故障診斷研究較少，大多數(shù)故障診斷研究的對(duì)象都是高速軸承［7-9］，也沒有文獻(xiàn)對(duì)HMM進(jìn)行深刻的探討和分析。因此，以轉(zhuǎn)盤軸承為研究對(duì)象，利用經(jīng)驗(yàn)?zāi)B(tài)分解（Empirical Mode Decomposition，EMD）對(duì)故障信號(hào)進(jìn)行特征提取［10-11］，通過HMM對(duì)特征參數(shù)進(jìn)行建模分析，并從HMM診斷精度與訓(xùn)練樣本數(shù)的關(guān)系、故障類型數(shù)目對(duì)HMM診斷精度的影響等方面對(duì)HMM進(jìn)行探討。

1 基于EMD-HMM的轉(zhuǎn)盤軸承故障診斷流程

1.1 EMD算法

EMD算法的目的是通過對(duì)非線性、非平穩(wěn)信號(hào)進(jìn)行分解獲得一系列表征信號(hào)特征時(shí)間尺度的固有模態(tài)函數(shù) （Intrinsic Mode Function，IMF），分解后原始信號(hào)由若干個(gè)IMF分量ci（t）和1個(gè)余項(xiàng)rn（t）構(gòu)成，即

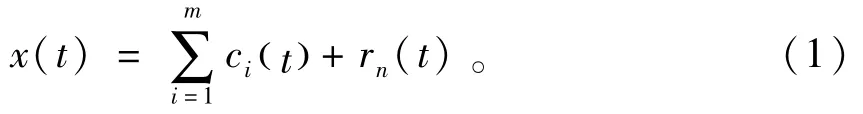
1.2 HMM的基本原理

HMM可以用5個(gè)元素進(jìn)行描述，包括2個(gè)狀態(tài)集合和3個(gè)概率矩陣：

1）模型的狀態(tài)數(shù)目N。記N個(gè)狀態(tài)為S＝｛S1，S2，…，SN｝，t時(shí)刻模型所處的狀態(tài)為qt。

2）每一狀態(tài)下對(duì)應(yīng)的觀測(cè)值數(shù)目M。記M個(gè)觀測(cè)值為V＝｛v1，v2，…，vM｝，t時(shí)刻的觀測(cè)值為Ot。

3）狀態(tài)轉(zhuǎn)移概率矩陣A，A＝｛aij｜i，j＝1，2，…，N｝，此處僅考慮一階HMM，當(dāng)前所處狀態(tài)qi僅與前一時(shí)刻所處狀態(tài)有關(guān)，即

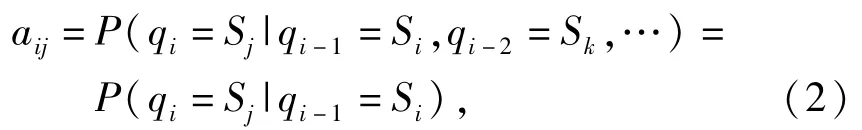
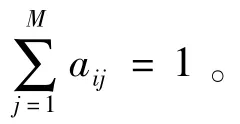
4）觀測(cè)值概率矩陣B，B＝｛bjk｜j＝1，2，…，N；k＝1，2，…，M｝，其中

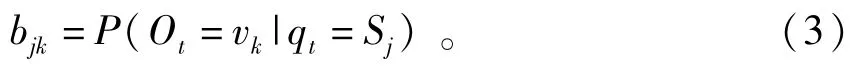
5）初始狀態(tài)概率向量π，π＝［π1，π2，…，πN］，用于描繪觀測(cè)序列O在t＝1時(shí)刻所處狀態(tài)q1的概率分布，即

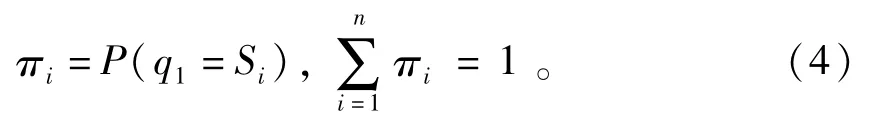
綜上，HMM的參數(shù)可以簡(jiǎn)化為λ＝（A，B，π）。

1.3 故障診斷流程

基于EMD-HMM的轉(zhuǎn)盤軸承故障診斷步驟如下［12］：

1）采集振動(dòng)信號(hào)。

2）根據(jù)轉(zhuǎn)盤軸承的故障狀態(tài)將信號(hào)分為I類，每類中包含J組同種故障數(shù)據(jù)。由于轉(zhuǎn)盤軸承轉(zhuǎn)速慢，故障頻率主要集中在低頻，因此先對(duì)各組信號(hào)進(jìn)行小波降噪，濾除高頻部分，然后進(jìn)行EMD處理，得到若干個(gè)IMF分量，選取每組中包含主要故障信息的前K個(gè)IMF分量。

3）提取各IMF分量的能量。

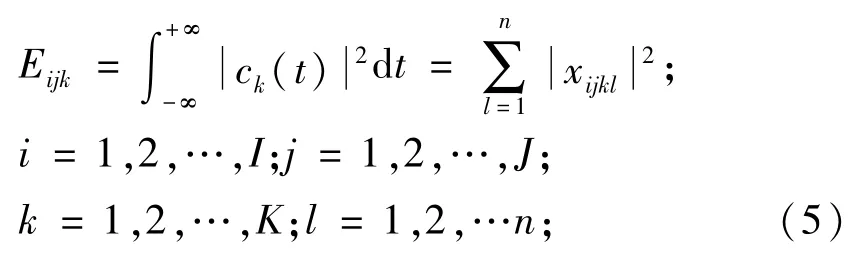
式中：xijkl為各點(diǎn)幅值；i為轉(zhuǎn)盤軸承第i種故障狀態(tài)；j為第j組數(shù)據(jù)；k為第k個(gè)IMF分量，l為第l點(diǎn)。

4）將各組中IMF分量的能量組成特征向量

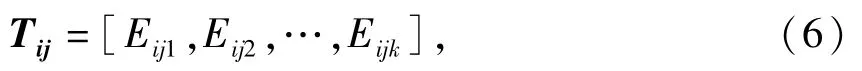
然后將特征向量組成特征向量矩陣T＝［T11，T12，…，T1J；T21，T22，…T2J；…；TI1，TI2，…，TIJ］T。

5）對(duì)特征向量矩陣T進(jìn)行歸一化處理，得到新的特征矢量矩陣T′。

6）初始化HMM模型的狀態(tài)轉(zhuǎn)移概率矩陣A，觀測(cè)值概率矩陣B和初始狀態(tài)概率向量π，然后將歸一化后的特征矢量矩陣輸入到HMM模型中進(jìn)行訓(xùn)練，訓(xùn)練完成后得到由I個(gè)HMM組成的分類器HMMs。

7）將測(cè)試樣本同樣進(jìn)行上述處理，然后輸入至訓(xùn)練好的HMMs，計(jì)算每次輸入的lg P（O｜λ），產(chǎn)生最大的對(duì)數(shù)似然函數(shù)輸出值所對(duì)應(yīng)的HMM，即為轉(zhuǎn)盤軸承當(dāng)前的運(yùn)行狀態(tài)，即

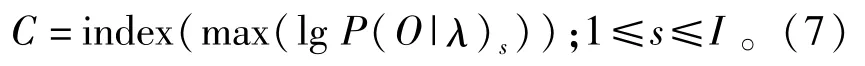
診斷過程如圖1所示。

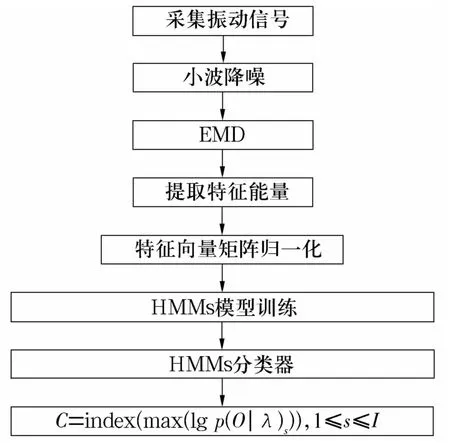
圖1 診斷方法流程圖Fig.1 Flow chart of diagnosis method

2 轉(zhuǎn)盤軸承加速疲勞壽命試驗(yàn)

試驗(yàn)所用轉(zhuǎn)盤軸承的型號(hào)為QNA730-22，試驗(yàn)臺(tái)結(jié)構(gòu)如圖2所示，按照J(rèn)B／T 2300—2011《回轉(zhuǎn)支承》進(jìn)行加速疲勞壽命試驗(yàn)［13］。

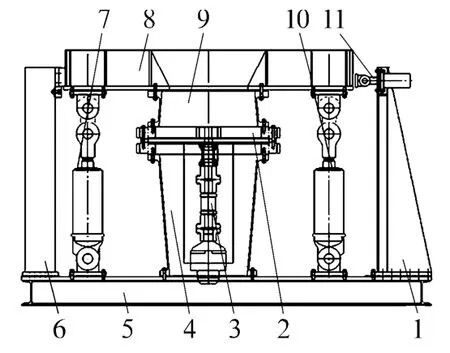
圖2 轉(zhuǎn)盤軸承試驗(yàn)臺(tái)結(jié)構(gòu)示意圖Fig.2 Schematic of test rig for slewing bearing

試驗(yàn)結(jié)束后拆機(jī)檢查，發(fā)現(xiàn)外圈溝道出現(xiàn)嚴(yán)重破損，內(nèi)圈出現(xiàn)了點(diǎn)蝕，部分鋼球產(chǎn)生了疲勞破損，多根螺栓也出現(xiàn)斷裂，如圖3所示。

圖3 轉(zhuǎn)盤軸承損傷零件Fig.3 Damage parts of slewing bearing

3 試驗(yàn)結(jié)果分析

3.1 方法驗(yàn)證

根據(jù)試驗(yàn)結(jié)果，將故障狀態(tài)分為外圈故障、內(nèi)圈故障、鋼球故障、單個(gè)螺栓斷裂故障、多個(gè)螺栓斷裂故障5種，并結(jié)合正常狀態(tài)各采集60組數(shù)據(jù)，采樣頻率為2 048 Hz，每組數(shù)據(jù)長(zhǎng)1 s，共2 048個(gè)點(diǎn)。整個(gè)試驗(yàn)過程中采集到的加速度信號(hào)如圖4所示。

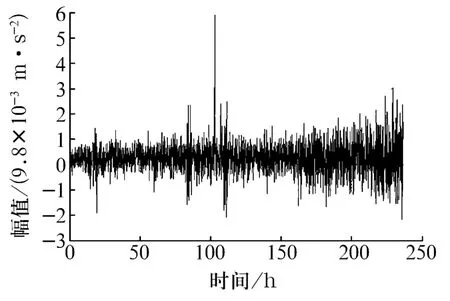
圖4 全壽命試驗(yàn)加速度信號(hào)趨勢(shì)圖Fig.4 Trend of acceleration signal during full-life experiment

在此，選取外圈故障、單個(gè)螺栓斷裂故障、多個(gè)螺栓斷裂故障以及正常狀態(tài)4個(gè)狀態(tài)進(jìn)行討論，每種狀態(tài)取5組樣本作為訓(xùn)練樣本，取20組樣本作為測(cè)試樣本。

3.1.1 特征提取

由于轉(zhuǎn)盤軸承轉(zhuǎn)速慢、其故障特征頻率一般位于5 Hz之內(nèi)［14］。因此，首先對(duì)采集到的振動(dòng)信號(hào)進(jìn)行小波消噪，濾除10 Hz以上的頻率部分；然后對(duì)其進(jìn)行EMD處理，求取前7個(gè)IMF分量的能量；最后依據(jù)診斷流程得到歸一化的特征矢量矩陣 T′。

3.1.2 故障診斷

數(shù)據(jù)處理完畢后，將訓(xùn)練樣本導(dǎo)入到HMM模型中進(jìn)行訓(xùn)練，訓(xùn)練時(shí)的收斂誤差為10-4，即當(dāng)輸出相似概率的變化小于10-4時(shí)訓(xùn)練終止。訓(xùn)練時(shí)選取最大迭代步數(shù)為50。

模型訓(xùn)練結(jié)束得到轉(zhuǎn)盤軸承正常狀態(tài)、外圈故障、單個(gè)螺栓斷裂故障、多個(gè)螺栓斷裂故障的HMMs分類器。然后將測(cè)試樣本輸入分類器，得到各狀態(tài)的輸出概率，對(duì)數(shù)似然概率值反映了特征向量與各個(gè)HMM的相似程度，對(duì)數(shù)似然概率值越大，特征向量越接近該狀態(tài)HMM，特征向量屬于使輸出對(duì)數(shù)似然概率值最大的模型所對(duì)應(yīng)的故障類型，選取似然概率最大的故障狀態(tài)類型作為輸出結(jié)果。診斷結(jié)果如圖5所示。

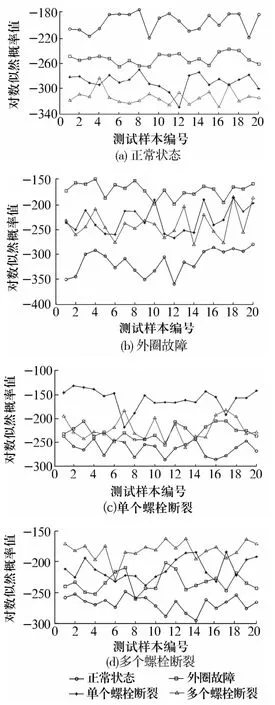
圖5 轉(zhuǎn)盤軸承各故障狀態(tài)的HMM模型測(cè)試結(jié)果Fig.5 HMM model test results of slewing bearing under various states

從圖5中可以看出：正常狀態(tài)HMM模型的分類比較清晰，而外圈故障、單個(gè)螺栓斷裂和多個(gè)螺栓斷裂狀態(tài)均存在個(gè)別交叉現(xiàn)象，具體診斷結(jié)果見表1。由表可知：利用較少的樣本訓(xùn)練HMM模型基本可以識(shí)別出不同的故障狀態(tài)，平均識(shí)別率達(dá)到92.5%，診斷精度尚可。

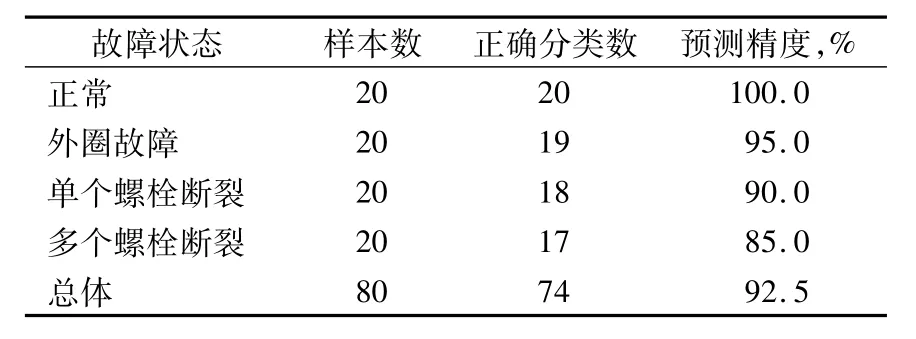
表1 轉(zhuǎn)盤軸承各故障狀態(tài)的HMM診斷結(jié)果（20組樣本）Tab.1 HMM diagnostic results under four states of slewing bearing（20 groups samples）

3.2 訓(xùn)練樣本數(shù)與診斷精度的關(guān)系

訓(xùn)練樣本只有5組時(shí)，診斷精度并不是很高，于是嘗試通過增加訓(xùn)練樣本數(shù)來研究HMM模型診斷精度的變化情況。考慮到轉(zhuǎn)盤軸承試驗(yàn)困難、成本較高、周期長(zhǎng)，利用現(xiàn)有條件開展了小樣本數(shù)下HMM診斷精度變化的研究，訓(xùn)練樣本數(shù)變化范圍為5～40，測(cè)試樣本數(shù)為20。具體分析步驟與3.1相同，統(tǒng)計(jì)結(jié)果見表2，訓(xùn)練樣本數(shù)與HMM診斷精度的關(guān)系如圖6所示。

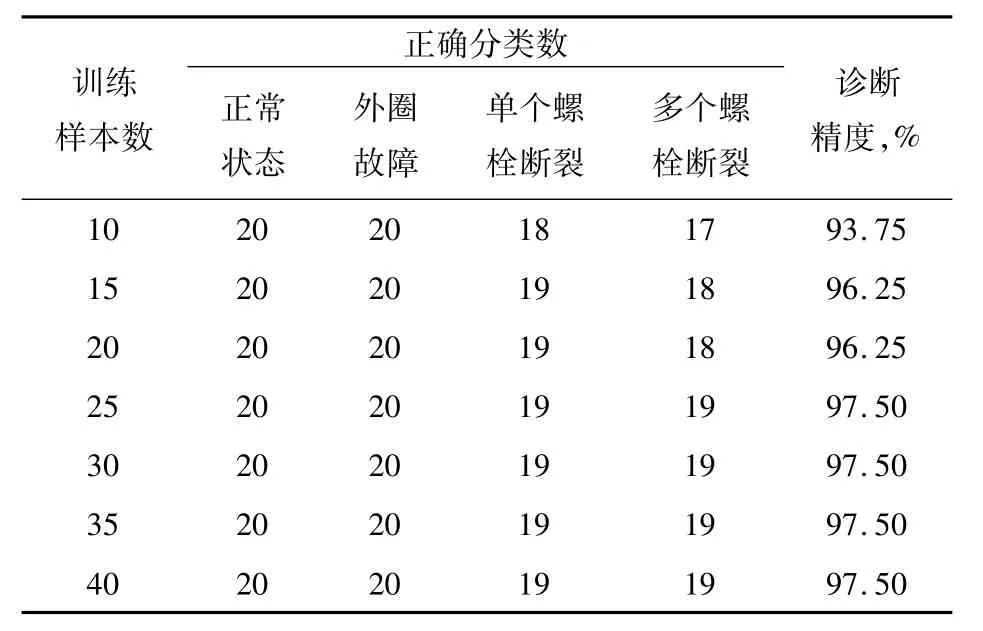
表2 不同訓(xùn)練樣本數(shù)下轉(zhuǎn)盤軸承的HMM診斷結(jié)果Tab.2 HMM diagnostic results of slewing bearing under different training samples

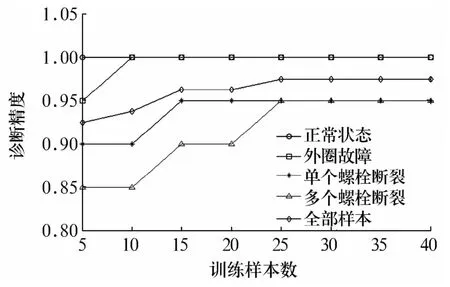
圖6 訓(xùn)練樣本數(shù)與HMM診斷精度的關(guān)系Fig.6 The relationship between HMM diagnosis accuracy and training samples

試驗(yàn)表明：HMM模型的診斷精度隨著樣本數(shù)的增加而提高，當(dāng)訓(xùn)練樣本數(shù)增加到25組時(shí)，總體精度達(dá)到97.50%，再增加訓(xùn)練樣本時(shí)，診斷精度不再增加，說明訓(xùn)練樣本數(shù)增加到一定數(shù)量時(shí)，HMM診斷精度趨于平穩(wěn)。

3.3 故障類型數(shù)對(duì)HMM診斷精度的影響

根據(jù)采集到的振動(dòng)信號(hào)，在之前研究的基礎(chǔ)上，分別增加1種故障類型（內(nèi)圈故障）和2種故障類型（內(nèi)圈故障和鋼球故障），對(duì)不同故障類型下HMM診斷精度的變化進(jìn)行研究，統(tǒng)計(jì)結(jié)果如圖7所示。

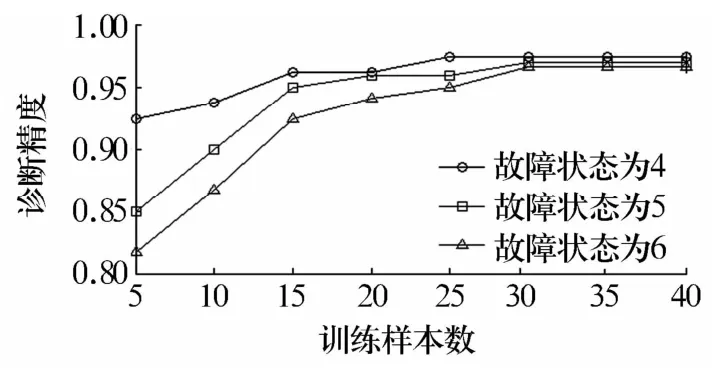
圖7 HMM診斷精度與故障類型數(shù)目的關(guān)系Fig.7 The relationship between HMM diagnosis accuracy and number of fault types

從圖7可以看出：在相同的訓(xùn)練樣本數(shù)下，故障類型越多，診斷精度越低；而當(dāng)訓(xùn)練樣本增加到一定數(shù)量時(shí)，3種故障類型的診斷精度都趨于平穩(wěn)，且診斷精度都較高。說明故障類型的數(shù)目對(duì)HMM診斷精度有比較大的影響，也就是說，要達(dá)到同一精度，故障類型越多，所要求的訓(xùn)練樣本數(shù)越多。

4 結(jié)論

針對(duì)轉(zhuǎn)盤軸承故障信號(hào)非線性、非平穩(wěn)性的特點(diǎn)，采用EMD提取特征向量并使用HMM進(jìn)行模式識(shí)別，并經(jīng)試驗(yàn)分析得到以下結(jié)論：

1）該方法能夠及時(shí)穩(wěn)定地對(duì)轉(zhuǎn)盤軸承進(jìn)行分析，很好地識(shí)別轉(zhuǎn)盤軸承的故障狀態(tài)，適用于低速重載轉(zhuǎn)盤軸承的故障診斷。

2）HMM的診斷精度隨著樣本數(shù)的增加而提高，而當(dāng)訓(xùn)練樣本增加到一定數(shù)量時(shí)，診斷精度趨于平穩(wěn)，接近100%。

3）故障類型的數(shù)目對(duì)HMM的診斷精度有較大影響，若要達(dá)到同一精度，故障類型越多，所要求的訓(xùn)練樣本數(shù)越多。當(dāng)訓(xùn)練樣本增加到一定數(shù)量時(shí)，不同故障類型數(shù)目的診斷精度都趨于平穩(wěn)并接近100%。