基于雙模量理論的高強度鋼環肋圓柱殼總體穩定性塑性修正方法

張海寬，邱昌賢，陸 波

（1.海軍駐431廠軍代表室，遼寧 葫蘆島 125004；2.中國船舶科學研究中心，江蘇 無錫 214082）

基于雙模量理論的高強度鋼環肋圓柱殼總體穩定性塑性修正方法

張海寬1，邱昌賢2，陸 波2

（1.海軍駐431廠軍代表室，遼寧 葫蘆島 125004；2.中國船舶科學研究中心，江蘇 無錫 214082）

文章基于矩形截面壓桿的雙模量理論和高強度鋼的材料彈塑性本構關系，建立了環肋圓柱殼結構總體穩定性塑性修正曲線及修正方法，結果表明，模型的計算結果與靜水外壓試驗測得的塑性失穩壓力值及有限元結果符合情況較好，壓桿雙模量理論模型雖然和環肋圓柱殼實際結構存在差異，但由此得到的塑性修正方法仍具有較好的工程精度，在應用于高強度鋼環肋圓柱殼總體穩定性計算時適應性好，且形式簡單，便于運用。

總體穩定性；塑性修正；雙模量理論；環肋圓柱殼

0 引 言

在現代潛艇、潛水器的結構設計參數范圍內，以環肋圓柱殼為代表的耐壓殼體在靜水外壓下的失穩破壞往往發生在材料的塑性階段，彈性穩定性計算結果一般僅具有理論意義，可用于波形分析及結構初步評估，但不足以指導工程實際，同時，塑性穩定性的直接計算方法（包括有限元法）往往需要進行多次迭代，求解較為繁瑣、耗時，工程應用的便利性偏弱，因此，建立精度能滿足工程要求且較為簡便、實用的結構塑性穩定性修正方法是十分必要的。

近年來，隨著潛水器極限深度不斷加大，以及新型高強度鋼材及配套焊材、相關工藝的日益成熟和廣泛應用，高強度鋼耐壓結構的穩定性計算問題逐漸成為理論研究和工程實際面對的主要方向，為了解決新的問題，需要在傳統塑性修正方法基礎上，根據高強度鋼的材料力學特性進行推導并建立新的修正曲線。

殼體結構塑性失穩壓力的計算方法可以通過在薄殼彈塑性穩定性理論中引入材料本構關系來建立，但形式大多較為復雜。Timoshenko等[1-2，4-5]簡單地采用折算模量Er（Reduced Modulus）代替彈性模量E來求解臨界載荷，這是一種基于矩形截面壓桿彈塑性穩定性的雙模量理論，長期用于蘇俄潛艇耐壓圓柱殼結構的穩定性設計計算，也是國內現有規范方法的理論基礎，這種修正方法使用簡單，便于手算，且多年來經過了許多模型的試驗驗證，具有較好的工程精度，本文在對環肋圓柱殼的總體穩定性進行塑性修正時也將繼續采用這一理論。

折減模量Er是一個材料常數，與結構各點的空間坐標無關，但由其推導過程（見后文）可以看出，Er顯然與壓桿的截面形狀有關，唐家祥[3]計算了不同截面形狀對應的Er，其偏差約為5%，從而得到了Er對壓桿截面形狀并不敏感的結論，這成為本文利用雙模量理論對高強度鋼環肋圓柱殼結構的總體失穩壓力進行塑性修正的重要依據。同時，環肋圓柱殼結構發生總體失穩時，失穩形態對應的周向整波數通常為n=2或3，縱向半波數通常為m=1，塑性加載區和彈性卸載區并存，這和臨界失穩壓桿的微彎狀態十分相似，因此將環肋圓柱殼簡化為與軸心壓桿相同的物理模型是有一定合理性的。

本文將考慮高強度鋼的材料彈塑性本構關系，基于傳統的矩形截面壓桿雙模量理論進行推導，以期建立工程上方便應用的環肋圓柱殼結構總體穩定性塑性修正曲線，并對若干高強度鋼大尺度模型進行彈塑性計算、修正，將相關計算值和規范解、有限元解和試驗結果進行對比驗證，以檢驗該塑性修正方法的工程適用性和可靠性。

1 雙模量理論的塑性修正方法

環肋圓柱殼結構的實際失穩壓力往往顯著低于其彈性理論值，原因之一在于結構應力超過材料的比例極限后，應力—應變關系不再呈線性增長，彈性模量E迅速降低，因此需要針對材料的物理非線性特征對彈性失穩壓力進行塑性修正。材料的塑性應力—應變關系往往比較復雜，會給結構穩定性計算帶來很大困難，工程上一般的做法是：根據彈性穩定性理論得到結構的彈性失穩臨界壓力，再基于幾何修正系數Cg和物理修正系數Cs進行修正，得到實際的失穩壓力，其中幾何修正系數Cg可由具有初始形狀缺陷柱殼的大撓度彈性失穩臨界壓力和形狀完善柱殼的小撓度彈性失穩臨界壓力之比得到，而物理修正系數Cs可由形狀完善柱殼的小撓度彈性失穩臨界壓力和塑性失穩臨界壓力之比得到，也可根據雙模量理論、切線模量理論或薄殼彈塑性穩定性理論得到，本文將利用高強度鋼的拉伸性能參數，基于雙模量理論對穩定性塑性修正系數Cs進行推導，并開展模型試驗結果的對比驗證。

雙模量理論（Double Modulus Theory）首先由Considere等[2，7]提出，他們認為，壓桿除了直線形式的平衡外，還存在微彎狀態下的平衡，外力與內力的平衡是隨遇的（Neutral Equilibrium）。對處于臨界失穩狀態的微彎壓桿，隨著彎曲的發展，其凹側應力按材料切線模量Et增大（塑性加載），而凸側應力則按彈性模量E減小（彈性卸載），在此基礎上，Engesser[2，7]于1895年提出了雙模量理論，Von Karman[2，7]于1910年在其博士論文中推導了矩形截面壓桿的折減模量Er，用于計算粗短柱子在塑性狀態下的Euler載荷。

雙模量、切線模量等理論均建立在以下主要假設基礎上[3]：

（1）彎曲應力與彎曲應變之間的關系與材料單向拉、壓的應力、應變關系相同；

（2）壓桿的各橫截面在彎曲前后保持為平面，忽略截面翹曲。

在計算折減模量Er時，認為壓桿的軸向載荷在彎曲過程中不變，即彎曲拉、壓應力在橫截面上的合力為0，此外還需利用彎曲應力與外力矩之間的物理方程及壓桿應變與彎曲曲率之間的幾何關系（曲率計算式可根據微彎狀態的小變形假設進行簡化）。由于壓桿各點的彎曲變形由兩個模量確定，在材料的塑性階段，E與Et并不相等，因此截面中和軸與形心軸不重合。

對于微彎壓桿，將應力均取為絕對值，則附加的彎曲拉、壓應力σ1（凸側）和σ2（凹側）為：

對于矩形截面壓桿，彎曲應力的合力R1、R2分別為：

由于壓桿的軸向力在彎曲過程中不變，因此合力R1=R2，得到：

代入h=h1+h2，得到：

壓桿矩形截面上的彎矩為：

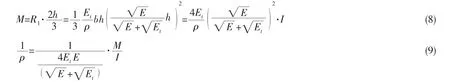
對于微彎狀態（小變形），近似認為y’=0，則有：

從而得到矩形截面壓桿的折減模量和基于Euler公式的塑性穩定性修正系數：

2 高強度鋼材料本構關系及塑性修正曲線

對于高強度鋼，在塑性階段，材料的單向拉伸應力—應變關系同樣可用三參數方程（Ramberg-Osgood模型）來描述[5]，如（13）式所示，則其割線模量Es和切線模量Et可由應力—應變的彈塑性本構關系推導得到，如（14）、（15）式所示，在材料的彈性階段，Es和Et均與彈性模量E相等。

根據參考文獻[5]，對高強度鋼可取E=1.96×105MPa，m=6.811 8，K=557.89，則其材料的彈塑性本構關系如圖1～3中相關曲線所示。

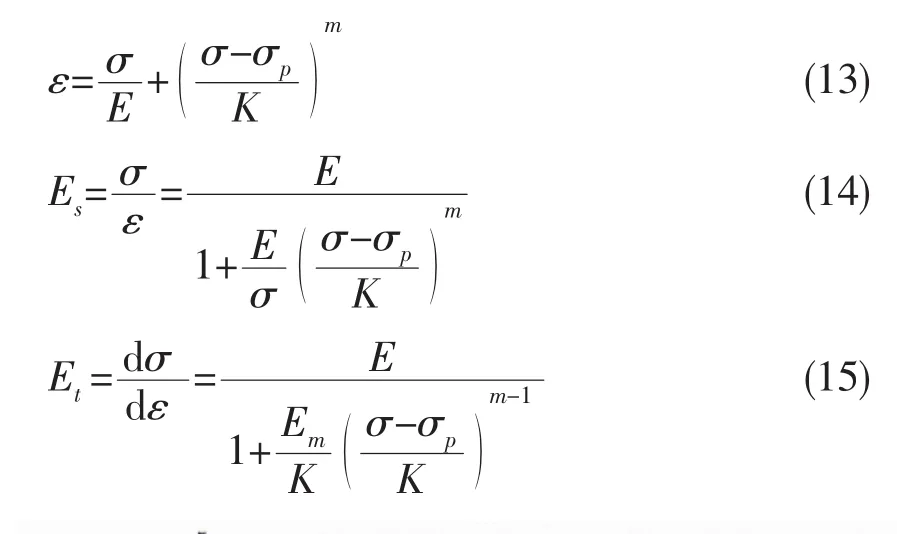
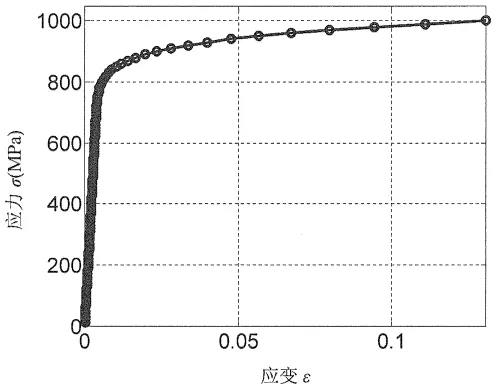
圖1 高強度鋼單向拉伸應力—應變關系曲線Fig.1 Stress vs strain curve for high strength steel under axial tension

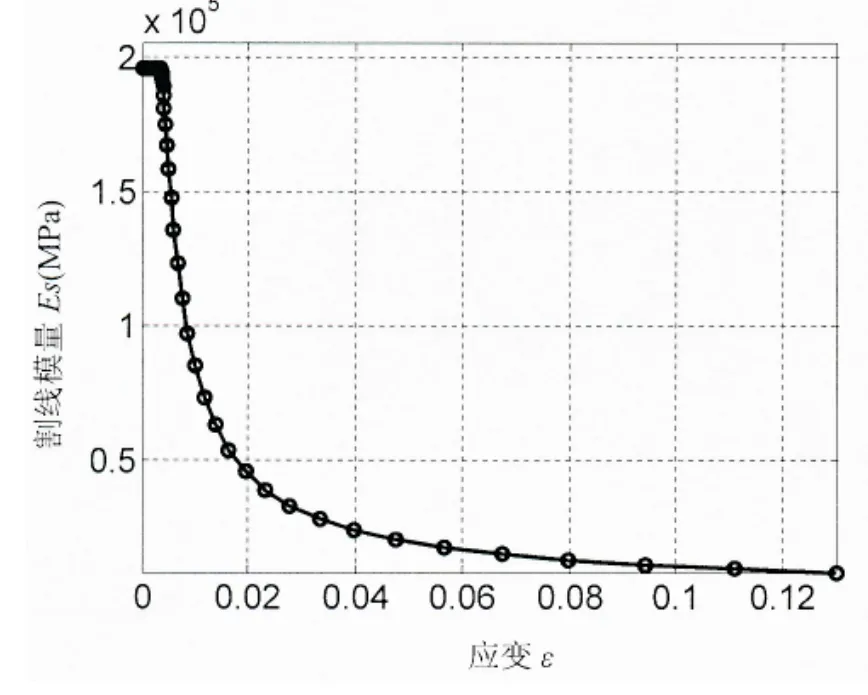
圖2 高強度鋼割線模量—應變關系曲線Fig.2 Secantmodulus vs strain curve for high strength steel

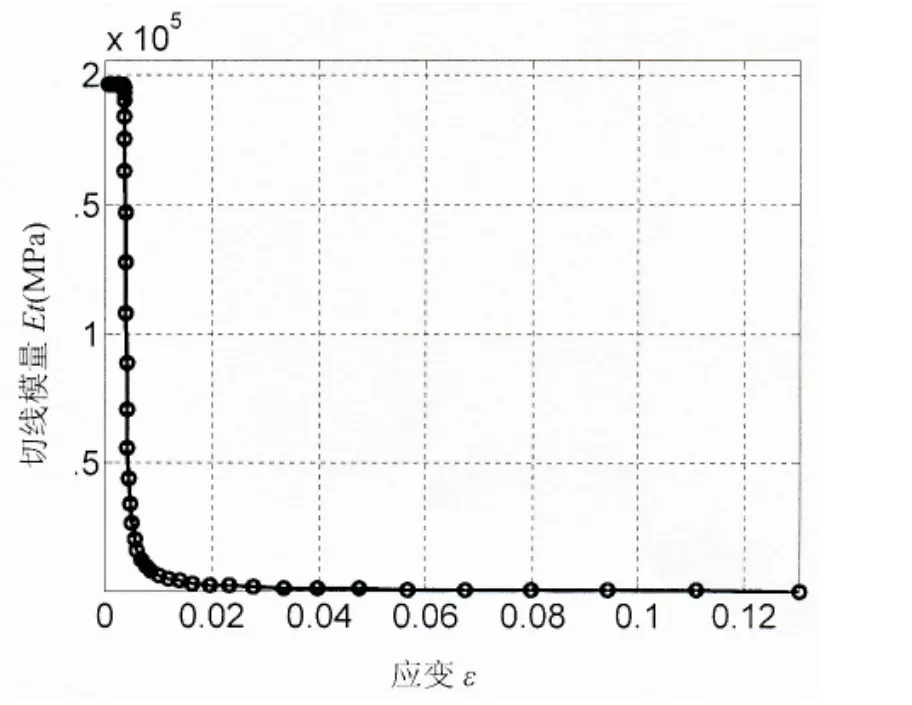
圖3 高強度鋼切線模量—應變關系曲線Fig.3 Tangentmodulus vs strain curve for high strength steel

利用高強度鋼拉伸曲線的特征參數求得折算模量Er、塑性穩定性修正系數Cs與結構應變的相對關系后，再經過由塑性應變向彈性等效應力σe的轉換，即可得到雙模量理論的環肋圓柱殼總體失穩臨界壓力的塑性修正曲線，如圖4所示，在等效應力σe低于比例極限σp時，取修正系數Cs=1。

為簡化穩定性的計算過程，假定失穩前環肋圓柱殼在靜水外壓作用下處于無矩狀態，計算周向應力時將肋骨截面積平均分配到殼板上：

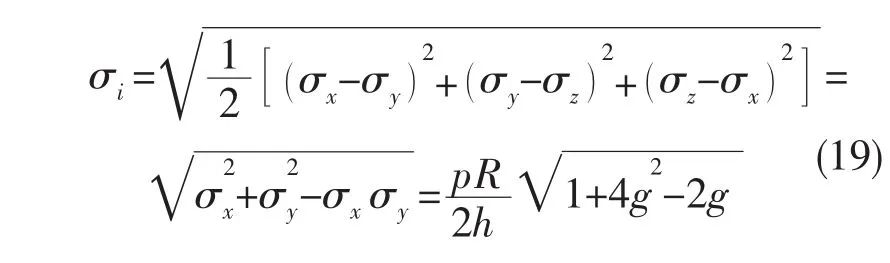
應注意到，規范中修正彈性總體穩定性時近似周向中面應力取為：

而本塑性修正曲線對應的彈性應力為等效應力，與現行規范方法有所不同：

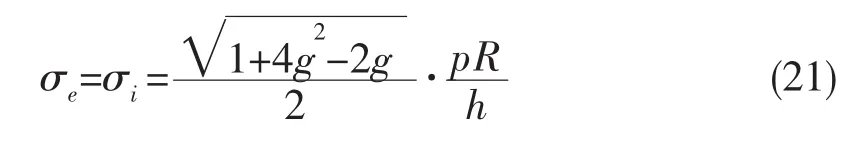
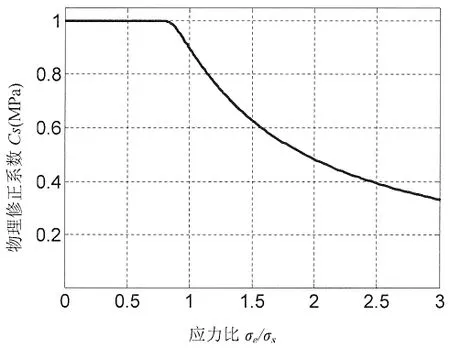
圖4 基于雙模量理論的高強度鋼穩定性塑性修正系數Cs曲線Fig.4 Plastic stability modification factor Csvs strain curve for high strength steel based on Double Modulus Theory

3 計算結果對比分析

為了考驗相關方法的可靠性，本文對CSSRC完成的若干高強度鋼環肋圓柱殼大尺度模型的總體穩定性進行了計算—在求得計及肋骨偏心的彈性總體失穩壓力后，利用所建立的高強度鋼環肋圓柱殼結構總體穩定性的物理非線性Cs曲線進行塑性修正，并將計算結果相比較，如表1所示。為了便于對比，所選擇的模型在靜水外壓試驗中均發生總體失穩，為了具有一定代表性，各模型的設計壓力、結構參數等均拉開一定差別，圓柱殼中面半徑與厚度之比R/t到在55到120之間。計算時取材料的彈性模量E=1.96×105MPa；泊松比μ=0.3，屈服強度Rp0.2為800MPa級。

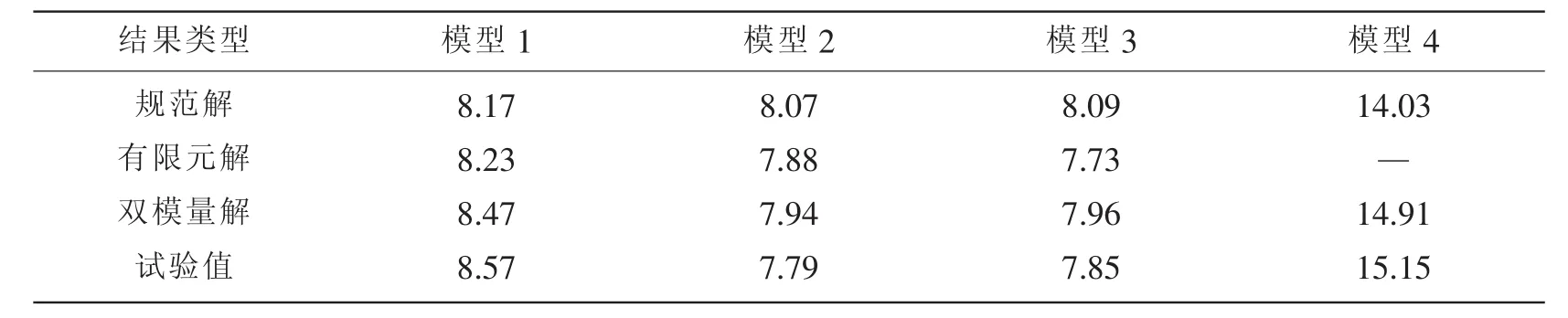
表1 高強度鋼模型塑性總體失穩壓力結果對比（MPa）Tab.1 High strength steel models’calculated critical pressure of plastic general stability(MPa)

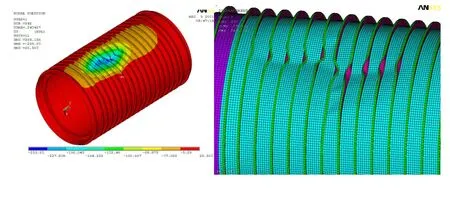
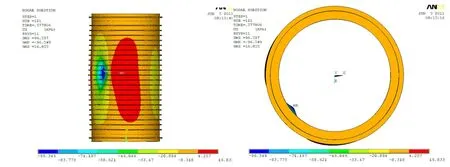
圖5 有限元分析得到的高強度鋼環肋圓柱殼靜水外壓總體失穩破壞形態及位移云圖Fig.5 FE buckled forms of ring-stiffened cylindrical shell models of high strength steel under external hydrostatic pressure

由表1可知，雙模量理論的塑性修正結果與規范解、有限元解和試驗值基本上相差不大，但雙模量解與規范解之間的差別依然存在一定差別，說明現行規范提供的修正方法對高強度鋼確實有適用性問題，方法的偏保守或是偏危險將決定耐壓結構的設計是否優化或安全儲備是否足夠，初步對比情況表明，雙模量計算值比規范解更接近于模型靜水外壓試驗結果，因而本文的塑性修正方法在應用于高強度鋼環肋圓柱殼結構總體穩定性計算時適應性更好。

4 結 語

為了研究采用高強度鋼制造的環肋圓柱殼結構在靜水外壓下的塑性總體穩定性，本文基于傳統的雙模量理論（DMT）研究并建立了工程上方便應用的穩定性塑性修正方法。為考驗相關方法的可靠性，本文采用現有的規范公式和ANSYS有限元程序對環肋圓柱殼結構模型的總體穩定性進行對比計算，主要工作及結論如下：

（1）基于矩形截面壓桿雙模量理論（DMT）和高強度鋼的材料彈塑性本構關系，建立了工程上方便應用的環肋圓柱殼結構總體穩定性塑性修正曲線及修正方法，該Cs修正曲線可針對材料具體的拉伸性能參數進行擬合及調整。

（2）在求得計及肋骨偏心的彈性總體失穩壓力的前提下，利用所建立的環肋圓柱殼結構總體穩定性的物理非線性Cs曲線進行塑性修正，相關計算值和模型靜水外壓試驗測得的塑性失穩壓力值、有限元結果符合情況較好。雖然矩形截面壓桿雙模量理論模型和環肋圓柱殼實際結構存在差異，但比較粗略的雙模量理論仍具有較好的工程精度，且形式簡單，便于運用。

（3）雙模量解與規范結果之間的有所差別，說明現行規范提供的修正方法對高強度鋼確實存在一定的適用性問題，方法的偏保守或是偏危險將決定耐壓結構的設計是否優化或安全儲備是否足夠，初步對比表明，雙模量計算值比規范解更接近于模型試驗結果，因而本文的塑性修正方法在應用于高強度鋼環肋圓柱殼總體穩定性計算時適應性更好。

（4）經初步驗證，本文建立的高強度鋼塑性修正曲線和修正方法是合理、可行的，所得到的研究成果和相關結論可為現行規范方法的修改完善提供技術支撐和參考建議，但相關方法的可靠性還有待試驗驗證、實踐檢驗和進一步補充完善。

參考文獻：

[1]鐵摩辛柯S P,蓋萊J M.彈性穩定理論[M].北京：科學出版社,1965,2：189-191.

[2]周承倜.彈性穩定理論[M].成都：四川人民出版社,1981,1：46-50.

[3]唐家祥,王仕統,裴若娟.結構穩定理論[M].北京;中國鐵道出版社,1989,10(1)：47-54.

[4]周承倜.薄殼彈塑性穩定性理論[M].北京：國防工業出版社,1979,12(1)：178-188.

[5]徐秉漢,朱邦俊,歐陽呂偉,裴俊厚.現代潛艇結構強度的理論與試驗[M].北京：國防工業出版社,2007,6(1)：57-58.

[6]GJB/Z 21A-2001.潛艇結構設計計算方法[S].國防科學技術工業委員會,2001.

[7]曾紀杰.對中柔度壓桿的雙模量理論的修正[J].機械強度,2006,28(3)：463-464.Zeng jijie.Revision of the formula with bimodulus im intermediate column[J].Journal of Mechanical Strength,2006,28 (3)：463-464.

Plastic modification methods based on Double Modulus Theory for general stability of ring-stiffened cylindrical shell of high strength steel

ZHANG Hai-kuan1,QIU Chang-xian2,LU Bo2
(1.Naval Representative Office in NO.431 Shipyard,Huludao 125004,China; 2.China Ship Scientific Research Center,Wuxi214082,China)

Considering elastic-plastic constitutive relationship of high strength steel,a plastic modification curve method,which was based on compressed pole with rectangular section under Double Modulus Theory,was proposed for calculating the general stability of ring-stiffened cylindrical shell structure.The calculated results were validated by some examples to meet with FEM results and buckled pressure of high strength steel models under external hydrostatic pressure pretty well.The theoretical model of compressed pole under Double Modulus Theory is a little different from the true structure of cylindrical shell,however, the derived plastic modification method from DMT offered pretty good precision in engineering sense.Besides,the method has simple form and easy to use.

generalstability;plastic modification;Double Modulus Theory;ring-stiffened cylindrical shell

U674.76

A

10.3969/j.issn.1007-7294.2017.07.011

1007-7294（2017）07-0888-07

2017-03-15

張海寬（1977-），男，工程師；

邱昌賢（1981-），男，高級工程師，E-mail：qiuchangxian163@163.com。