對2017年浙江選考卷中一個磁聚焦問題的釋疑
王金聚
(浙江省溫州中學,浙江溫州 325000)
對2017年浙江選考卷中一個磁聚焦問題的釋疑
王金聚
(浙江省溫州中學,浙江溫州 325000)
針對一個對磁聚焦前后帶電粒子的密度分布的錯誤認識,本文進行了深入的剖析.關鍵詞:磁聚焦;密度分布;錯誤認知;剖析
2017年浙江省高考物理選考試卷的最后一題是一道電磁學的大題,針對題中的第3個小問題,不少考生出現了一種典型的錯誤解法,甚至有的教師也存在同樣的錯誤認知,今單獨將其列出,給予詳細剖析,供大家參考.
原題.(2017年浙江選考卷第23題)如圖1所示,在xOy平面內,有一電子源持續不斷地沿x正方向每秒發射出N個速率均為v的電子,形成寬為2b,在y軸方向均勻分布且關于x軸對稱的電子流.電子流沿x方向射入一個半徑為R,中心位于原點O的圓形勻強磁場區域,磁場方向垂直xOy平面向里,電子經過磁場偏轉后均從P點射出,在磁場區域的正下方有一對平行于x軸的金屬平行板K和A,其中K板與P點的距離為d,中間開有寬度為2l且關于y軸對稱的小孔.K板接地,A與K兩板間加有正負、大小均可調的電壓UAK,穿過K板小孔到達A板的所有電子被收集且導出,從而形成電流.已知,d=l,電子質量為m,電荷量為e,忽略電子間相互作用.
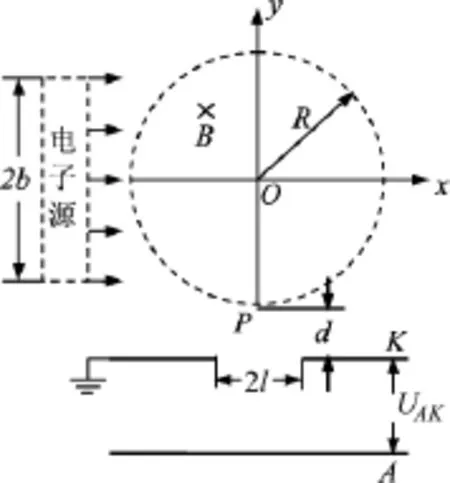
圖1
(1)求磁感應強度B的大小;
(2)求電子從P點射出時與負y軸方向的夾角θ的范圍;
(3)當UAK=0時,每秒經過極板K上的小孔到達極板A的電子數;
(4)畫出電流i隨UAK變化的關系曲線(在答題紙上的方格紙上).
(2)考慮最邊緣的電子,如圖2所示,設最上端的電子從P點射出時與負y軸的夾角為θm,由幾何關系可得
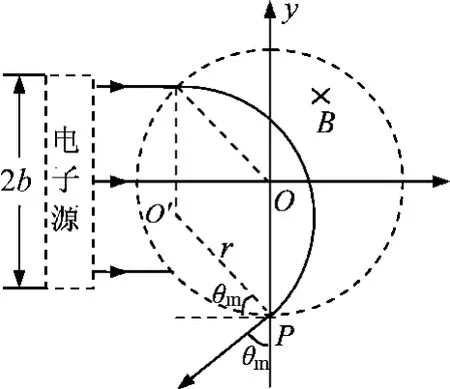
圖2
(3)如圖3所示,設P點與小孔的右邊緣的連線與豎直方向成φ角,因為d=l,所以φ=45°,所以
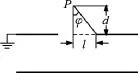
圖3
(4)略.
標準答案如下:
(2)如圖2所示,設上端電子從P點射出時與負y軸最大夾角為θm,由幾何關系得θm=60°.同理,下端電子從P點射出時與-y軸最大夾角也為60°,范圍是-60°≤θ≤60°.
矛盾及釋疑:比較可以看出,兩種解法在解答第(3)問時采取了不同的思路,且得出了不同的答案,孰是孰非?問題出在哪里呢?
帶電粒子通過磁場匯聚到一點的現象稱之為磁聚焦,題中的帶電粒子均聚焦于P點,過P點后再呈輻射狀離開磁場.從上面的解答可以看出,從P點射出時粒子的運動方向在與-y軸成60°角的左右范圍內.第一種解法的出發點是從粒子出場的角度比值來求解,這就有了一個“默認”作為前提——即認為既然粒子進場時在y軸方向上是均勻分布的,那么出場時在輻射的120°角范圍內各向的分布也應該是均勻的,這種看法對不對呢?
任取一粒子來分析,如圖4所示,設粒子從E點射入、P點射出,其軌道半徑為r,軌道的圓心為O′,連接OO′,由于O′E=OP=R,O′E=O′P=r,所以△OO′E △OO′P,所以有∠OO′E=∠OO′P,由于O′E平行于y軸,所以∠OO′E=∠O′OP,故有∠OO′P=∠O′OP,所以PO=PO′,即r=R,故四邊形OPO′E為菱形.設出場方向與-y軸方向成θ角,過P點作切線PD,由幾何關系可看出∠FOE=∠O′PD=θ,設E點的縱坐標為y,則,y與θ的取值是一一對應的關系,我們不妨等間距地取幾個y值,來對應算一下它們各自的出場角度,如表1所示.
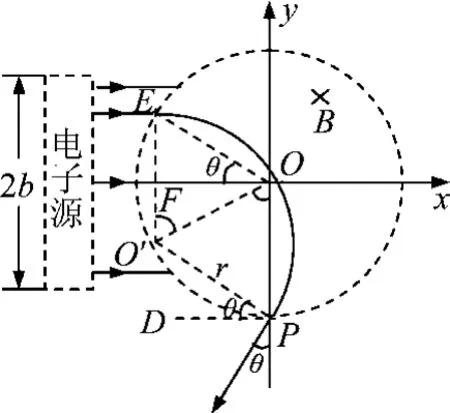
圖4

表1
依表中數據畫出粒子的對應軌跡如圖5所示.可以看出,在出場時粒子在各向的分布是非均勻的,越是靠近y軸的方向粒子分布越密集,向兩側密度逐漸減小.
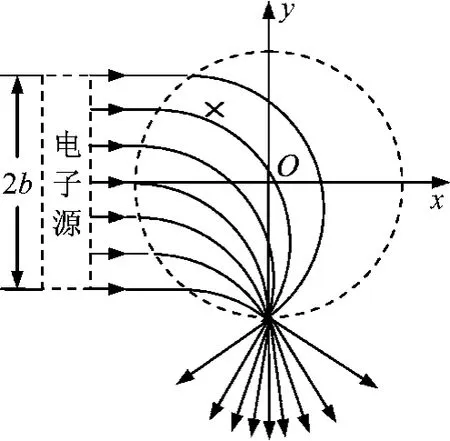
圖5
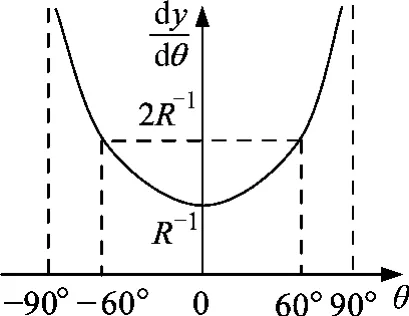
圖6
之所以會出現解法一中的錯誤認知,無非是一種想當然的思想在作祟.不仔細推導,就主觀地認為“均勻進”就似乎應該是“均勻出”,豈不知經過磁場的扭轉,不僅扭轉了粒子的方向,還同時扭轉了粒子的分布規律,使“均勻”變成了“不均勻”,所以說解題不能靠想當然,而是要靠有理有據的縝密推理.
2017-04-30)

