時滯反饋廣告模型的穩定性與分支分析"

張二麗，吳 卓

（1.鄭州財經學院信息工程學院，河南鄭州450044；2.澳洲國立大學，堪培拉2615）

時滯反饋廣告模型的穩定性與分支分析"

張二麗1，吳 卓2

（1.鄭州財經學院信息工程學院，河南鄭州450044；2.澳洲國立大學，堪培拉2615）

研究了廣告模型的時滯反饋，以時滯為參數，討論時滯對模型平衡點的穩定性和Hopf分支存在性的影響.研究發現當時滯處于一定范圍時，模型的平衡點穩定，并且會出現Hopf分支.最后，數值模擬驗證了理論結果.

時滯反饋；穩定性；Hopf分支

廣告是為了某種特定的需要，通過一定形式的媒體，公開而廣泛地向公眾傳遞信息的宣傳手段.通常是商品生產者、經營者和消費者之間溝通信息的重要手段，或企業占領市場、推銷產品、提供勞務的重要形式，主要目的是提高商品的銷量，擴大經濟效益.但并不是廣告越多，商品的銷售量就越大.當廣告超過一定限度后，消費者會對該商品產生某種逆反心理，甚至顧慮該商品是否有質量問題等等而影響顧客的購買量.當然，顧客購買該商品的速度還與該商品是否已經買足，與足夠用差多少有關系.于是文獻［1］建立了如下廣告與購物模型［1］

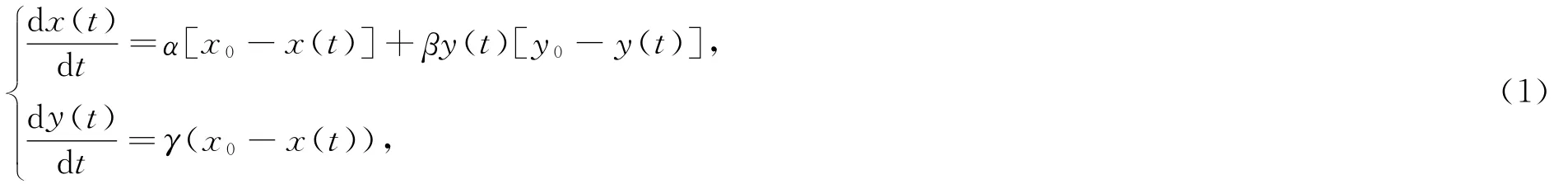
其中x（t）是對一種商品的購買水平，x0是最高需求水平，y（t）是對該商品的廣告量，y0是廣告量的最高限制，α，β，γ是正的常數，文獻［1］中給出了系統（1）平衡點的類型，并證明系統（1）不存在周期解.

為了預測商品的購買水平，在商品購買水平上增加一個時滯反饋，即在系統（1）的第一個方程上增加k［x（t）－x（t－τ）］，可得如下時滯反饋廣告模型

其中k是反饋增益，τ是正時滯.

1 平衡點的穩定性和Hopf分支存在性分析

本節將研究系統（2）的動力學行為.系統（2）有兩個平衡點P1（x0，0）和P2（x0，y0）.顯然，系統（2）與系統（1）有相同的平衡點.不失一般性，筆者研究平衡點P1，P2可做類似的研究.系統（2）在平衡點P1處的特征方程為

由RouthHuurwitz判據［2］可得引理1.

引理1 當τ＝0時，系統（2）的平衡點P1是漸近穩定的.

下面將研究時滯τ對系統（2）動力學行為的影響.即對系統（2）平衡點的穩定性與分支周期解存在性的影響.

設iω（ω＞0）是方程（3）的根.代入（3）并分離實部和虛部可得

將（4）中兩個方程平方相加可得

引理2［3］設

其中τi0（i＝1，2，…，m），p（i）j（i＝1，2，…，m；j＝1，2，…，n）是實常數.則當（τ1，τ2，…，τm）變化時，P（λ，e－λτ1，…，e－λτm）在右半開平面上的零點重數之和當且僅當有零根出現，在或穿過虛軸時才發生變化.

引理3 （i）如果α2＋4βγy0＞2kα，則方程（3）的所有根具有負實部.

（ii）如果α2＋4βγy0＝2kα，則當τ∈［0，τ00）時，方程（3）的所有根具有負實部，且當τ＝τ0j時，方程（3）有一對簡單純虛根±iω0，其中

（iii）如果α2＋4βγy0＜2kα，則當τ∈［0，τ0）時，方程（3）的所有根具有負實部，且當τ＝τ±j時，方程（3）有一對簡單純虛根±iω±，其中

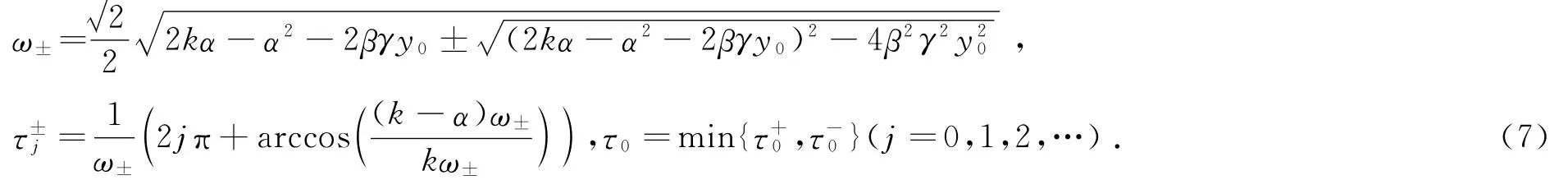
證 由方程（7）可得

當α2＋4βγy0＞2kα時，方程（5）無正實根.由引理2可得結論（i）成立.當α2＋4βγy0＝2kα時，方程（5）僅有一個正實根ω0＝.令如（6）式所定義，則（，ω0）是方程（5）的解，即λ＝±iω0是τ＝時方程（3）的一對純虛根，當τ＞0時，是使得方程（3）有根出現在虛軸上的第一個值，由引理2可得，當τ∈［0，τ00）時，方程（3）的所有根具有負實部，故結論（ii）成立.當α2＋2βγy0＜2kα時，方程（5）有兩個正根

令τj±如（7）式所定義，則（τj±，ω±）是方程（5）的解，即λ＝±iω±是τ＝τj±時方程（3）的一對純虛根，當τ＞0時，τ0是使得方程（3）有根出現在虛軸上的第一個值，由引理2可得，當τ∈［0，τ0）時，方程（3）的所有根具有負實部，故結論（iii）成立.引理2得證.

引理4 如果2kα＜α2＋2ω2＊＋2βγy0，則＞0；如果2kα＞α2＋2ω2＊＋2βγy0，則Re

證 對方程（3）兩邊關于τ求導得并注意到式（4），可得

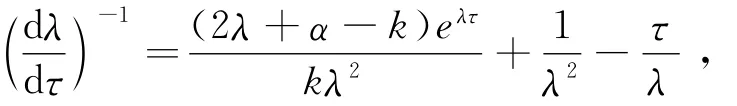
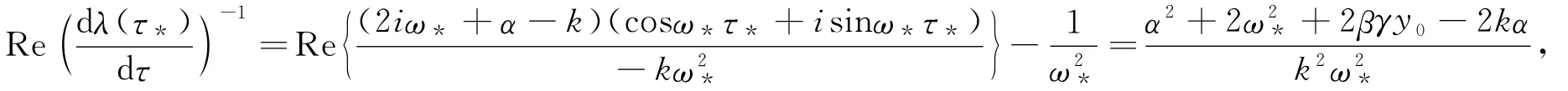
記與τ0相對應的ω±為ω0.由本文的引理1～4和文獻［4］中第11章的定理1.1，可以得到下面關于系統（2）的平衡點的穩定性與Hopf分支的存在性定理.

定理1 （i）如果α2＋4βγy0＞2kα，則當τ∈［0，＋!）時，系統（2）的平衡點P1漸近穩定.

（ii）如果α2＋4βγy0＝2kα，則當τ∈［0，τ00）時，系統（2）的平衡點P1漸近穩定；而且如果2kα≠α2＋2（ω0）2＋2βγy0，當τ＝τ0j（j＝0，1，2，…）時，系統（2）在平衡點P1處經歷Hopf分支.

（iii）如果α2＋4βγy0＜2kα，則當τ∈［0，τ0）時，系統（2）的平衡點P1漸近穩定；而且如果2kα≠α2＋2ω2±＋2βγy0，當τ＝τ±j（j＝0，1，2，…）時，系統（2）在平衡點P1處經歷Hopf分支.

2 數值模擬和結論

在系統（2）中取α＝0.28，β＝0.2，γ＝0.18，x0＝2，y0＝3.系統（2）的平衡點為P1（2，0）和P2（2，3）.由第1小節的討論可取k＝1，則α2＋4βγy0＝0.510 4＜0.56＝2kα，所以由引理3知方程（5）有兩個正根ω＋＝0.458 3和ω－＝0.235 6.再由（7）式和引理4可得

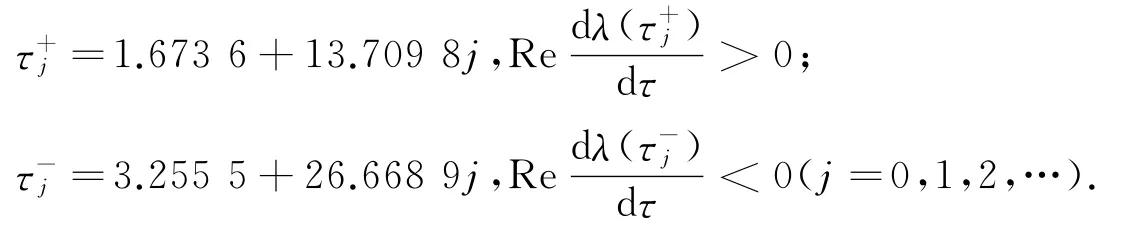
由定理1可得當τ＝0.89時，平衡點P1漸近穩定，如圖1所示；當τ＝1.673 6時，系統（2）在平衡點P1處經歷Hopf分支，如圖2所示.文獻［1］證明了系統（1）不存在周期解，而圖2表明系統（2）存在周期解，這說明時滯反饋對系統（1）的動力學行為有顯著的影響.

圖1 當τ＝0.2時，系統（2）的波圖和相圖

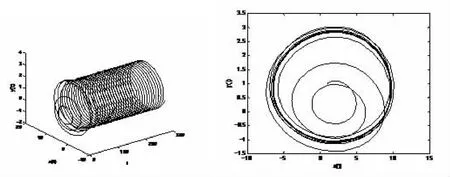
圖2 當τ＝1.673 6時，系統（2）的波圖和相圖

參考文獻：

［1］王樹禾.微分方程模型與混沌［M］.合肥：中國科學技術大學出版社，1999.

［2］馬知恩，周義倉，李承治.常微分方程定性與穩定性方法（2版）［M］.北京：高等教育出版社，2014.

［3］Ruan S G，Wei J J.On the zeros of transcendental function with applications to stability of delay differential equation with two delays［J］.Dynamics of Continuous，Discrete and Impulsive System，2003，10：863－874.

［4］Hale J K，Lunel S V.Introduction to functional differential equation［M］.New York：Springer-Verlag，1993.

Stability and Hopf bifurcation analysis of advertising model with time-delayed feedback

The advertising model with timedelayed feedback is studied.Taking the delay as parameter，we consider the effect of delay on the stability of equilibrium point and the existence of Hopf bifurcation.It is found that the equilibrium is stable and the Hopf bifurcation arises if time delay in a certain range.Finally，some numerical simulation are carried out to support the analytic results.

timedelay feedback；stability；Hopf bifurcation

ZHANG Erli1，WU Zhuo2
（1.School of Information Engineering，Zhengzhou Institute of Finance and Economics，Zhengzhou 450044，China；2.Australian National University，Canberra 2615）

O175.13

A

1671-9476（2017）02-0010-04

10.13450／j.cnkij.zknu.2017.02.003

2016-07-18；

2016-11-25

河南省高等學校重點科研資助項目（No.16A110038，No.17B110003）

張二麗（1983－），女，碩士，講師，研究方向：微分方程的穩定性與分支理論、數學建模.E－mail：isszel＠163.com.