基于終端滑模控制的情緒模型混沌同步

張 偉，周長芹

（鄭州航空工業管理學院理學院，河南鄭州450015）

基于終端滑模控制的情緒模型混沌同步

張 偉，周長芹

（鄭州航空工業管理學院理學院，河南鄭州450015）

研究了一類情緒模型的滑模控制混沌同步問題，根據Lypunov穩定性理論給出了實現同步的控制方案，仿真算例表明了方案的有效性.

混沌同步；情緒模型；滑模控制

最近30年，混沌同步引起了越來越多的關注［1－6］，例如：文獻［7］設計了一類多渦卷系統的有限時間滑模混沌同步問題，文獻［8］研究了分數階干擾觀測器的滑模控制問題，得到了系統滑模漸穩的充分條件.文獻［9］基于Terminal滑模控制研究了Duffling混沌系統的投影同步問題，文獻［10］研究了冠狀動脈高階滑模自適應混沌同步設計滑問題.文獻［11］建立了情緒的非線性動態模型，并分析了在沒有外界刺激的情況下，解所能表現的人的情緒變化過程.文獻［12］研究了受周期外界環境影響的Van der pol情緒模型.筆者研究一類三階情緒模型的滑模控制混沌同步問題，根據Lypunov穩定性理論給出了實現同步的控制方案.

1 主要結果

文獻［11］研究了二階情緒系統的穩定性問題，系統描述為：

其中x（t）表示一種情緒的變化過程，γ，k為系統參數，當表示快樂情緒的變化時，變量x（t）表示快樂的幅度隨時間推移的變化，上式等價于如下系統：

以上述系統為驅動系統，設計響應系統為

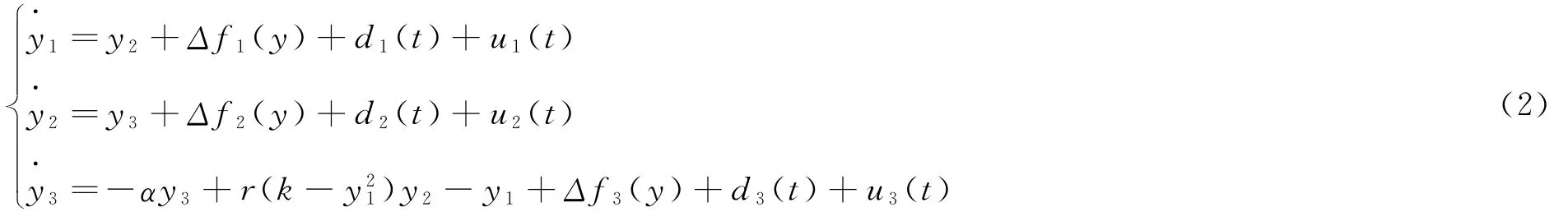
定義系統誤差ei（t）＝yi（t）－xi（t），i＝1，2，3.將（2），（1）兩式相減得：

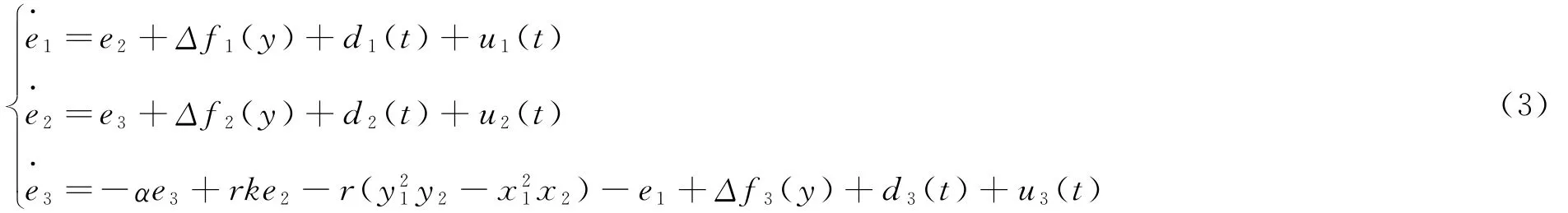
當α＝0.5，r＝5.6，k＝1時，系統出現混沌吸引子.

假設1 不確定項Δfi（y）＜mi，外部擾動di（t）＜ni；mi，ni＞0（i＝1，2，3）

假設2 mi，ni＞0（i＝1，2，3），未知.

引理1 假設存在連續的正定函數V（t）滿足微分不等式

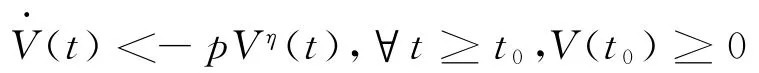
式中p＞0，0＜η＜1為兩個正常數，則對任意給定的t0，V（t）滿足如下不等式：

V1－η（t）#V1－η（t0）－p（1－η）（t－t0），t0#t#T.并且V（t）#0，tT，其中

引理2 設有實數a1，a2，…，an，0＜q＜2，則有下述不等式成立

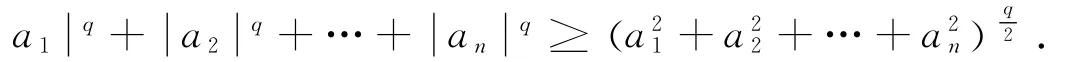
對于誤差系統（3），設計非奇異終端滑模面：

其中λi＞0，0＜λi＜1.

引理3［13］（Barbalat引理）若函數f（t）在［0，＋!）上一致連續，并且廣義積分∫＋!0f（t）dt存在，則有

定理1 誤差系統（3）在非奇異終端滑模面（4）上，系統的軌跡在有限區間ts內達到平衡點，其中：ts#

其中μ＝min｛λi｝，i＝1，2，3，μ＞0，由引理2得：

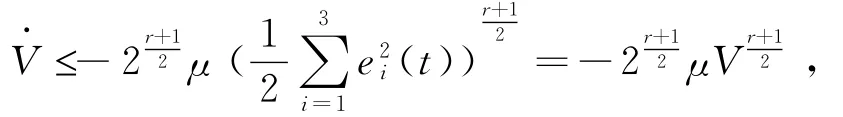
由引理1，

設計控制律：

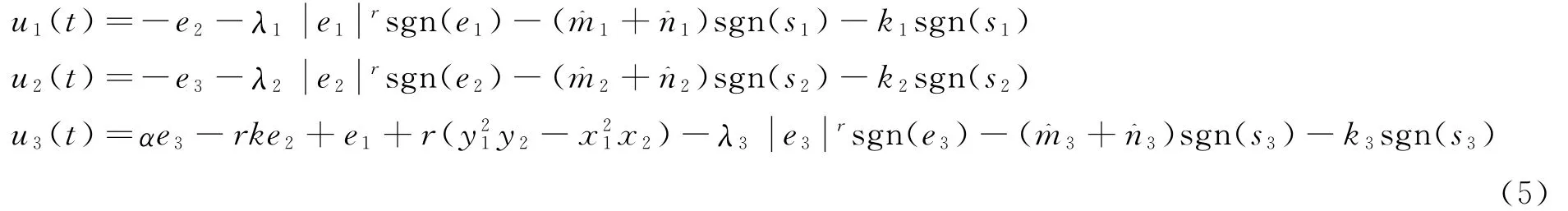
其中m＾i，n＾i為mi，ni的估計值，ki＞0為增益.

定理2 對誤差系統（3）在控制器及自適應律（6）的作用下，誤差狀態軌跡能達到滑模面.

證 選取Lyapunov函數

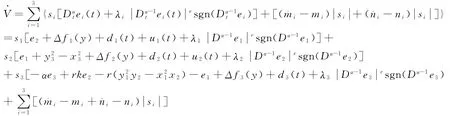
再根據假設條件1，2，很容易得到：

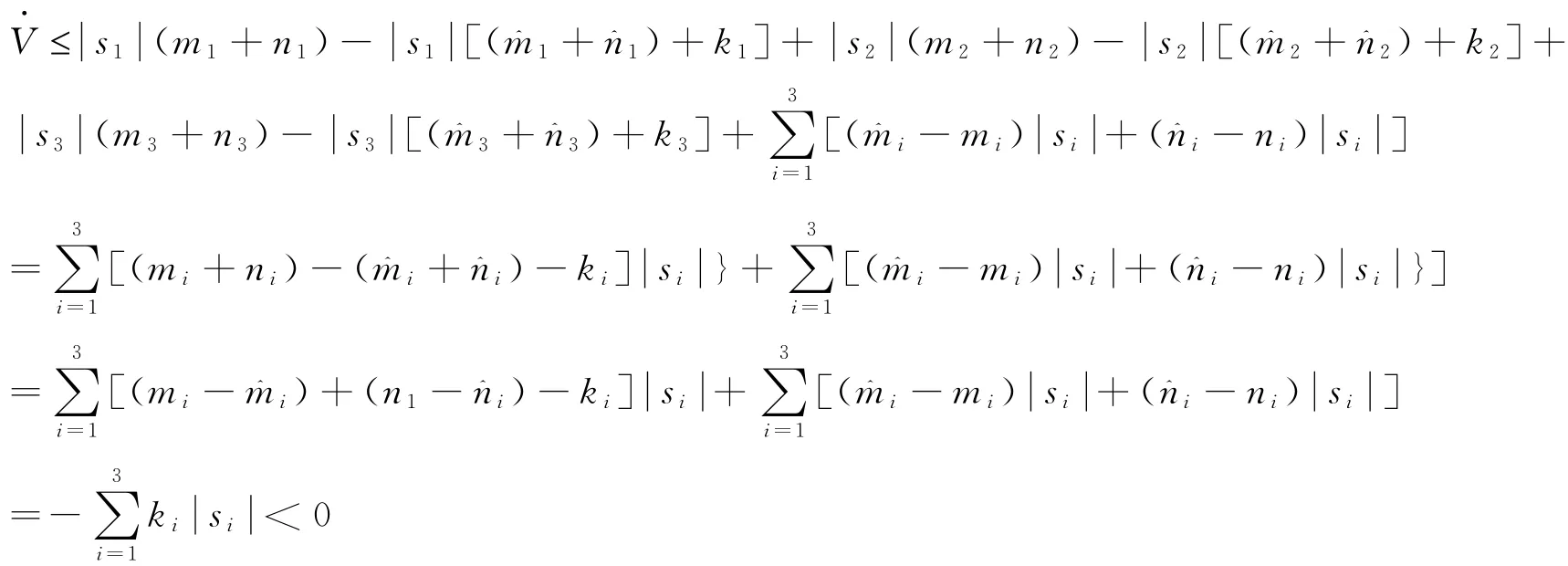
所以si（t）是可積的且有界，由于，在閉區間［0，ts］上si（t）滿足一致連續性，根據引理3（Barbalat引理）可知，si（t）→0，

2 數值仿真

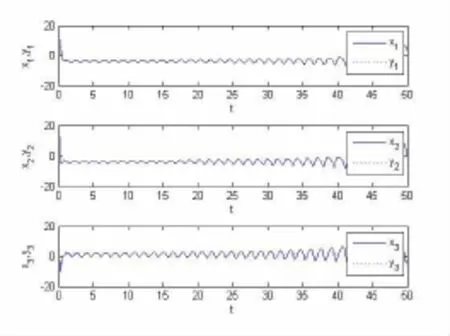
圖1 主從系統狀態

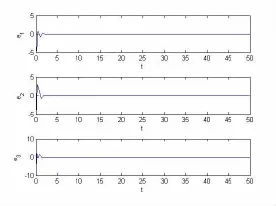
圖2 系統誤差曲線

3 結論

根據Lypunov穩定性理論研究了一類情緒模型的滑模同步問題，給出了主從系統實現同步的滑模控制方案，設計了滑模面和控制器，仿真算例表明了方案的有效性.

［1］賀尚宏，謝進，程杰鋒，等.非線性單擺動力系統多參數混沌邊緣的研究［J］.機械傳動，2015，39（8）：1－4.

［2］Bagley RL，Torvik P J.On the appearance of the fractional derivative in the behavior of real materials［J］.J Appl Mech，1984，51（4）：294－298.

［3］Bagley RL，Torvik P J.Fractional calculus in the transient analysis of viscoelastically damped structures［J］.AIAA J，1985，23（6）：918－925.

［4］Bagley RL.Power law and fractional calculus model of viscoelasticity［J］.AIAA J，1989，27（10）：1412－1417.

［5］Delavari H，Ghaderi R，Ranjbar A，et al.Fuzzy fractional order sliding mode controller for nonlinear systems［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15（4）：963－978.

［6］Lin TC，Lee T Y，Balas V E.Adaptive fuzzy sliding mode control for synchronization of uncertain fractional order chaotic systems［J］.Chaos，Solations and Fractals，2011，44（10）：791－801.

［7］李潔，黃艷賓，石丁丁，等.多渦卷系統的有限時間滑模控制［J］.科技通報，2015，31（1）：183－185.

［8］王歡，王思聰.帶有干擾觀測器的分數階滑模控制［J］.電光與控制，2015，22（5）：89－92.

［9］陳志偉，高巖波，陸國平.Duffling混沌系統基于Terminal滑模控制的投影同步［J］.南通大學學報（自然科學版），2013，12（1）：24－29.

［10］趙占山，張靜，丁剛，等.冠狀動脈系統高階滑模自適應混沌同步問題［J］.物理學報，2015，64（21）：5081－5088.

［11］李力，周昌樂.基于范德波爾方程的情緒模型［J］.廈門大學學報（自然科學版），2011，50（4）：703－706.

［12］邢偉，茅青海.受周期外界環境影響的Van der pol情緒模型［J］.數學建模及其應用，2016，5（1）：43－48.

［13］梅生偉，申鐵龍，劉志康.現代魯棒控制理論與應用［M］.北京：清華大學出版社，2003.

Terminal sliding mode chaos synchronization of emotion models systems

ZHANG Wei，ZHOU Changqin
（College of Science，Zhengzhou University of Aeronautical，Zhengzhou 450015，China）

The paper studied the sliding mode chaos synchronization of emotion models based on Lyapunov stability theory.The sufficient conditions for the emotion models systems realized sliding mode chaos synchronization is concluded.Numerical simulations verify the feasibility of the proposed method.

chaos synchronization；emotion models；sliding mode control

O482.4

A

1671-9476（2017）02-0024-04

10.13450／j.cnkij.zknu.2017.02.006

2016-10-22；

2016-11-27

國家自然科學青年基金（No.NSFC11501525）；河南省科技廳軟科學項目（No.142400411192）

張偉（1978－），男，山東菏澤人，講師，碩士，主要研究方向：混沌同步.Email：zw2211＠zzia.edu.cn