改進PCA方法在化工過程中的故障診斷研究

杜海蓮，苗詩瑜，杜文霞，劉小亮

(1.河北師范大學 職業技術學院 河北 石家莊 050024；2.北京交通大學 電氣工程學院 北京 100044；3.石家莊鐵道大學 四方學院 河北 石家莊 051132)

改進PCA方法在化工過程中的故障診斷研究

杜海蓮1，苗詩瑜2，杜文霞1，劉小亮3

(1.河北師范大學 職業技術學院 河北 石家莊 050024；2.北京交通大學 電氣工程學院 北京 100044；3.石家莊鐵道大學 四方學院 河北 石家莊 051132)

為了使化工生產中復雜系統的故障判斷更加精準、更加有說服力，采集系統正常工作和故障狀態時的數據，運用改進的主元分析(PCA)算法判斷系統是否有故障產生。改進的主元分析算法是在傳統主元分析的基礎上將平方預測誤差SPE統計量分化成與主元顯著關聯的檢測變量殘差(PVR)統計量和其余一般變量殘差(CVR)統計量，再與Hotelling’sT2統計量相配合進行系統故障的判斷，使檢測到的結果更加精準，生產過程更加安全。將此改進的主元分析方法運用到田納西—伊斯曼過程中，仿真結果驗證了該方法可以有效識別系統處于正常工況狀態還是故障狀態，是一種系統故障分析和診斷的有效方法。

主元分析；故障診斷；生產安全

現代化工生產過程日趨復雜，系統中的變量增多，如傳感器個數多，需要檢測的數據很龐大，檢測起來有一定的困難，并且不同的生產系統組成不盡相同，都有自身的特殊性，不適用同一種檢測規律進行檢測，而主元分析(principal component analysis,PCA)解決了這個問題。主元分析算法是利用系統自身的正常工作數據進行建模，之后再根據輸入的工作數據進行故障的判斷，解決了系統不同所導致的檢測規律不通用的問題，使算法的使用范圍大大擴大，并提供了便利的檢測方法[1-3]。

傳統的主元分析方法能夠成功的將一些系統中的故障信息反饋出來，是通過平方預測誤差SPE(squared prediction error)統計量(即Q統計量)和Hotelling’sT2統計量來檢測，若有工作數據超出了控制限的大小，說明該系統在這一采樣點處有故障出現，便于通知給工作人員進行檢查[4-6]。

但是這兩個統計量導致有四種檢測結果出現，其中當Hotelling’sT2統計量可以看出很顯著的變化而SPE統計量幾乎看不出變化時無法準確判斷是系統工作狀態發生了變化還是真的有故障產生，而解決這一缺陷的方法，是將SPE統計量進行分離[7-9]，這樣一來，就有四個統計量一起對系統進行檢測，準確度得到了提升，更重要的是這種方法可以準確的告訴工作人員是否確有故障發生。

文獻[7]將這種方法運用到粘菌素發酵過程中，得到了有效的故障檢測結果，并且檢測的結果更加精確，工作效率更高；文獻[8]應用改進的主元分析方法，并以β-甘露聚糖酶發酵過程為對象，得到了有效的統計量檢測圖；文獻[9]應用改進的PCA算法檢測了雙效蒸發過程的故障，同樣得到了有效的檢測結果；而文獻[10]則是運用傳統的主元分析進行鍋爐系統的故障診斷，通過比較傳統和改進的PCA兩種方法，可以看到改進后的主元分析更加可靠。

以上文獻均是將主元分析方法運用到個別的實際系統中進行檢測，但是隨著生產系統的日趨復雜繁瑣，也為了保證此方法確實可靠準確，還應該將該方法應用到更加復雜的生產系統中，如田納西—伊斯曼系統，這種系統的生產過程非常復雜繁瑣，其系統內部以及各個部分之間的數據聯系也非常龐大，將其作為評價過程控制和監測方法的基準，在此系統中進行改進的主元分析的檢驗是非常可靠的。

1 傳統主元分析方法

傳統主元分析方法的主要步驟是：首先從工程現場采集系統各個傳感器的工作數據信息建立一個m×n的矩陣X，其中：m為采樣點個數，n為傳感器個數也即該系統中所要檢測的變量個數。通過主元分析的建模算法在這些變量中得到b個主元變量，因為這b個變量對系統最終檢測到的數據變化的貢獻率>85%，它們提供的數據信息量已經達到了我們對于生產過程檢測的精度要求。之后再對這些主元數據構成的矩陣進行分解和分析，算出平方預測誤差SPE(即Q統計量)和T2兩個統計量指標，以及它們各自的控制限，通過MATLAB平臺畫出相應的圖觀察是否有故障發生。

下面介紹傳統PCA具體建模算法：將檢測到的現場數據組成m×n的矩陣X，m可以理解為在一定時間內在m個不同的時間點采集了m組數據，即為m個采樣點，每一次采集的數據中又包括了n個變量(傳感器)的信息,用下式表示：

X=(x1,x2,…,xm)T。

(1)

其中，每一個xi都是一個行向量，有n個參數，即每一個xi代表一個采樣點的數據。

但由于一般從生產現場采集過來的每一個傳感器的數據單位都不相同，所以在進行主元算法建模之前要對這些數據進行標準化處理，標準化處理的方式有很多，其中一種標準化處理方式是將原始數據矩陣中的數據減去其相應傳感器此次檢測的所有數據的均值，再除以其方差，可以得到標準化后的矩陣Y，具體公式為：

(2)

Y矩陣的協方差矩陣S為：

(3)

得到協方差S后，便可以求取主元個數了，首先求出S的特征值λi和特征向量P，并將特征值按照由大到小排列，即λ1≥λ2≥λ3≥…≥λn≥0

根據累計貢獻率得出主元個數，將特征值從大到小逐次相加，將每一次的和除以所有特征值的和，當結果達到85%及以上時的特征值個數即為主元個數b，公式為：

(4)

因b個主元對于最終的數據變化提供的貢獻達到了85%以上，提供的數據信息量可以達到精度要求。此時，矩陣Y就可以分解為主元空間和殘差空間兩部分，即：

Y=TPT+M。

(5)

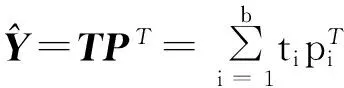
(6)

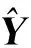
至此，主元分析的建模部分就結束了，之后計算兩個統計量的大小及其控制限，并將數據放入程序畫出圖像比較是否數據超出了控制限即可，若超出了說明有故障產生，若都在控制限以下說明系統正常運行。

首先SPE統計量Q為：

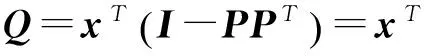
(7)

控制限為Qα：

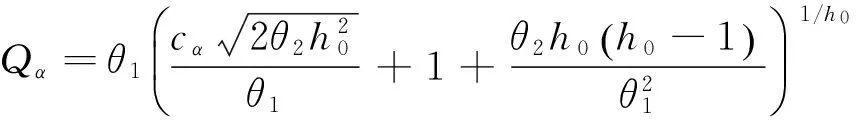
(8)

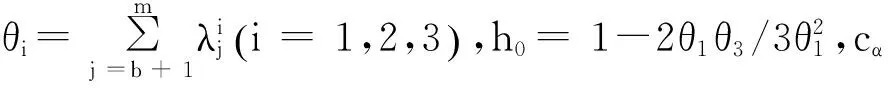
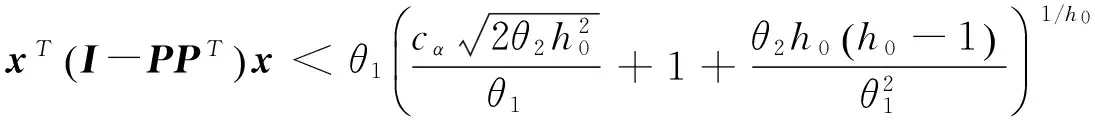
(9)

此時說明工作正常，沒有故障產生，否則說明系統工作不正常。

T2統計量為：

T2=xTPΛ-1PTx。

(10)

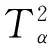
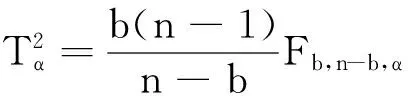
(11)

其中：Fb,n-b,α是自由度為b,n-b，置信度為α的F分布臨界值。

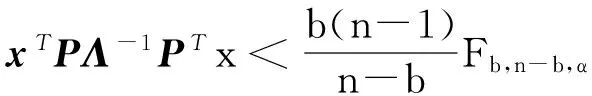
(12)

此時說明系統正常工作，否則屬于不正常狀態。

SPE統計量稱為平方預測誤差，檢測的是系統中所檢測變量的變化，SPE統計量超過控制限時說明變量之間的相關性發生了變化，有過程故障產生；只有T2統計量發生變化時說明可能有工況的變化發生，但變量之間的相關性依然滿足。所以當T2統計量有顯著變化，而SPE統計量沒有顯著變化時無法判斷是工況引起的變化還是系統確有故障產生，使得檢測效果不好，精確度不高。

通過分析得知，T2統計量檢測的是與主元顯著相關的變量的信息，而SPE統計量檢測的是被檢測數據的殘差的信息，所以我們只要把SPE統計量中與主元相關的變量分離出來就可以與T2統計量更好的相配合檢測系統故障。

2 改進的主元分析

傳統的主元分析算法中用到了SPE和T2兩個統計量，首先要指出SPE統計量統計的是正常建模數據本身內部數據之間的聯系是否遭到破壞及遭到破壞的程度，T2統計量統計的是檢測到的(噪聲)數據與主元子空間的距離，又由于T2統計量本身包括主元子空間和殘差子空間，所以T2統計量的控制限比SPE統計量的控制限要大的多。而且T2統計量檢測與主元明顯關聯的那些檢測變量的信息，SPE統計量檢測變量殘差的信息，兩種統計量的重點也并不一致。

以上兩種統計量檢測出來的結果有四種：SPE有很大變化而T2沒有明顯變化，此情況說明變量之間的相關性發生了變化，系統有故障產生；兩者都沒有明顯變化說明沒有故障產生，系統正常運行；兩者都有明顯變化說明系統有故障產生，但是當T2有明顯變化，而SPE沒有明顯變化時，就分不清是工況發生了變化還是數據之間的聯系遭到了破壞，不能準確的檢測出故障的原因，所以針對此不利因素，對傳統的主元分析按照以下的方法進行改進。

假設過程變量中與主元顯著相關的變量有s個，它們構成的殘差統計量為PVR(principal-component-related variable residual)統計量，其余的(n-s)個變量構成的殘差的統計量為CVR(common variable residual)統計量，即將SPE統計量分成了兩個統計量PVR和CVR，并有：

(13)

(14)

通過計算過程變量與主元的復相關系數可以確定s的大小，復相關系數的平方為：

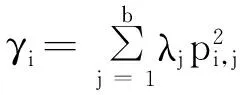
(15)

其中：pi,j是特征向量P的元素，λi是特征值。

復相關系數的平方反映某個變量被主元概括了多少信息[8]。

s的確定方法是：將算出的相關系數中大于0.85的系數相加，那么這些被加入到其中的相關系數個數即為s，通過這些系數的和可以算出wPVR，從而也可以算出wCVR的值，進而得到兩個統計量的大小，實現改進的主元分析的故障診斷。

接下來建立PVR和CVR統計量的控制限：

Qα=PVRα+CVRα=wPVRQα+wCVRQα，

(16)

PVRα=wPVRQα，

(17)

CVRα=wCVRQα，

(18)

wCVR=1-wPVR，

(19)

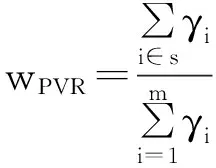
(20)

s表示與主元相關的過程的變量。由此就將SPE統計量分解成了兩個統計量，這樣使檢測的結果更加精確。最終檢測與傳統的主元分析進行比較，判斷改進的分析方法是否提高精確度。

3 改進的PCA在田納西伊斯曼過程的應用

3.1 田納西伊斯曼過程

田納西伊斯曼過程(TennesseeEastmanProcess,TEprocess),是Downs和Vogel提出的一種標準測試(Benchmark)過程。田納西伊斯曼過程包括41個測量變量和11個控制變量。這些數據包含正常狀態和21種不同的故障，每種狀態包括訓練部分和測試部分，分別為480和960組數據，可見田納西伊斯曼過程的數據非常龐大，各部分之間的聯系也是非常緊密的，正是由于田納西伊斯曼系統很強的代表性，因此可以將田納西伊斯曼過程作為評價過程控制和監測方法的基準工業過程。根據此系統提供的數據來驗證改進后的主元分析方法是否提高故障檢測的準確性，其過程如圖1所示。

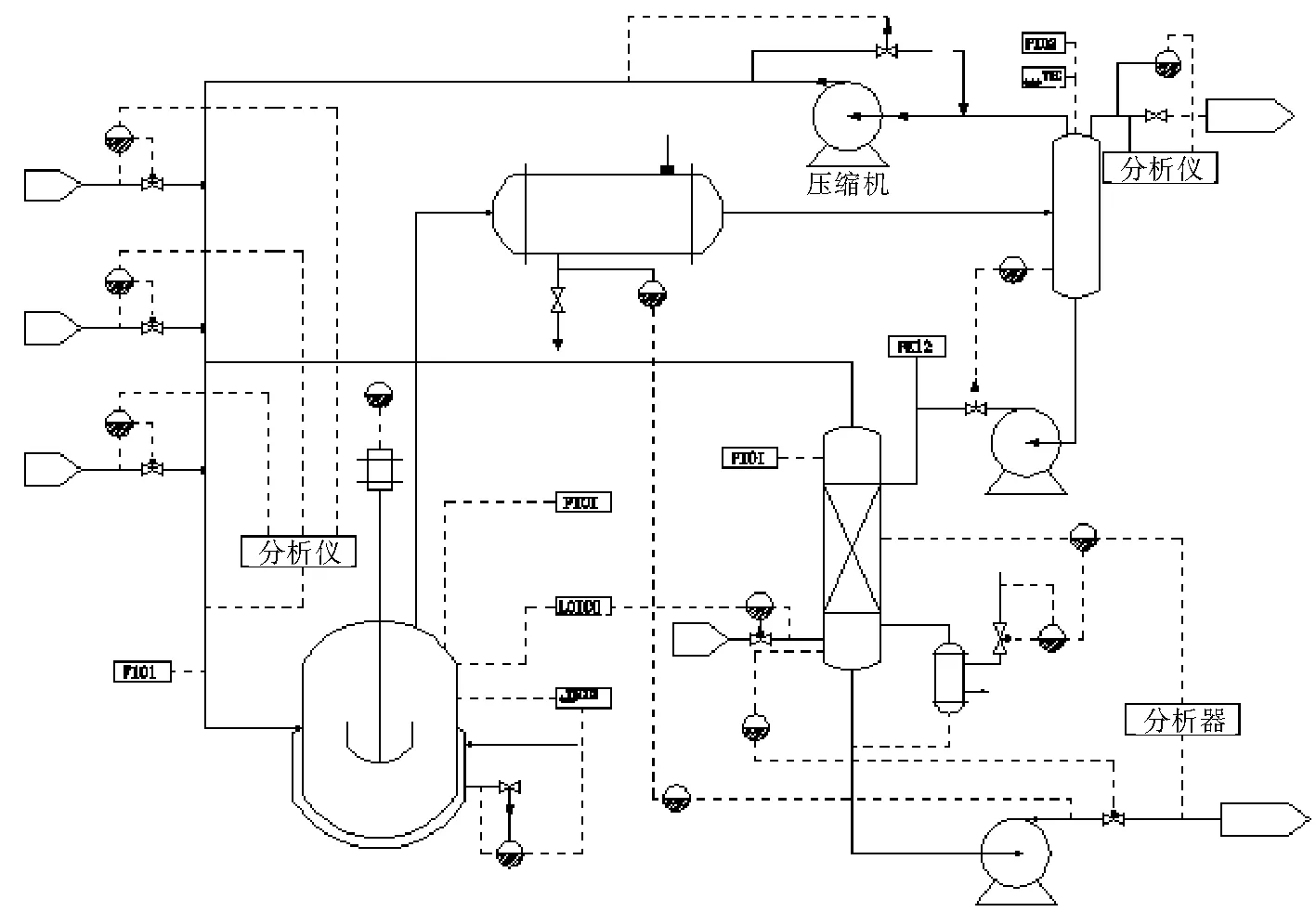
圖1 田納西伊斯曼過程示意圖

3.2 改進的PCA方法檢測故障結果分析

給該系統設置不同的故障，得到相應的故障數據，再次代入到程序中，得到的檢測結果如圖2所示：

圖2 故障4時數據檢測圖

在故障4中，故障產生的原因是田納西伊斯曼系統中的反應器冷卻水入口溫度發生階躍變化，分別用傳統主元分析和改進主元分析進行檢測的圖示如圖2所示：

在第162個采樣點之后的數據使得SPE統計量發生了顯著變化，在這一部分可以確定明過程變量之間的相關性發生了變化，且還看到PVR統計量有非常明顯的超過控制限的現象，又進一步說明了系統的過程變量發生了變化，確有故障產生。

但是在第162采樣點之前，T2統計量超過了控制限，而SPE統計量沒有明顯變化，無法判斷是工況的變化還是故障引起的變化，這時可以看到PVR統計量明顯超過了控制限，因此可以判定是這部分也有故障發生。

可見，利用改進的主元分析方法可以更加準確地判定故障產生與否。

在故障10中，故障產生的原因是物料C溫度隨機變化，同樣檢測得到的結果如圖3所示。

圖3 故障10數據檢測圖

由圖3可見，同樣在SPE統計量162個采樣點之后有明顯的變化，說明有故障產生，結合PVR統計量更加證實了這一結論，但在162采樣點之前SPE統計量的變化并不明顯，只是T2統計量有變化產生，也同樣判斷不出是否有故障產生，通過觀察PVR統計量便可以確定有故障產生，因為與主元顯著相關的過程變量有明顯的超過控制限的現象。

通過以上分析可以看出改進的主元分析方法不僅可以檢測出系統中的故障，而且結果更加準確，更加詳細，可以分清楚是工況的變化還是故障的產生，有效的保證了系統的安全性能。

4 小結

運用改進的主元分析對田納西伊斯曼過程進行檢測，用正常數據建模，之后用工作數據進行故障的判斷，并通過仿真實驗結果分析，主元分析檢測出了復雜系統的生產過程的故障問題，為復雜系統的安全性問題提供了便捷的檢測和故障診斷方式，對之前故障數據不明確的缺陷有了改進，應用改進的主元分析方法進行系統的故障檢測，結果準確度更高和效率更高。

[1]WANG Y F,MA X D,JOYCE M J.Reducing sensor complexity for monitoring wind turbine performance using principal component analysis [J].Renewable Energy,2016,97:444-456.

[2]GAO X,HOU J.An improved SVM integrated GS-PCA fault diagnosis approach of Tennessee Eastman process [J].Neurocomputing,2016,174(22):906-911.

[3]XU X Z,XIE L,WANG S Q.Multimode process monitoring with PCA mixture model[J].Computers & Electrical Engineering,2014,40:2101-2112.

[4]ZHOU B,YE H,ZHANG H F,LI M L.Process monitoring of iron-making process in a blast furnace with PCA-based methods [J].Control Engineering Practice,2016,47:1-14.

[5]PAN Y,YANG C,AN R,et al.Fault detection with improved principal component pursuit method[J].Chemometrics & Intelligent Laboratory Systems,2016,157(1):111-119.

[6]周東華，李鋼，李元.數據驅動的工業過程故障診斷技術[M].北京：科學出版社，2011:23-27,58-59.

[7]肖應旺，徐保國.改進PCA在發酵過程監測與故障診斷中的應用[J].控制與決策，2005，20(5):571-574. XIAO Yingwang,XU Baoguo.Application of improved PCA in the fermentation process monitoring and fault diagnosis [J].Control and Decision,2005,20(5):571-574.

[8]張新榮，熊偉麗，徐保國.基于Q統計量分量的故障檢測算法研究[J].計算機與應用化學，2008，25(12):1537-1542. ZHANG Xinrong,XIONG Weili,XU Baoguo.A study of approach on fault detection based on Q statistic component[J].Computers and Applied Chemistry,2008,25(12):1537-1542.

[9]王海清，宋執環，李平.改進PCA及其在過程監測與故障診斷中的應用[J].化工學報，2001，52(6):471-475. WANG Haiqing,SONG Zhihuan,LI Ping.Improved PCA with application to process monitoring and fault diagnosis[J].Journal of Chemical Industry and Engineering,2001,52(6):471-475.

[10]李傳金，王文標，花義峰，等.基于主元分析的鍋爐系統故障檢測與診斷[J].機電信息，2016(24):92-93. LI Chuanjin,WANG Wenbiao,HUA Yifeng,et al.Fault detection and diagnosis of boiler system based on principal component analysis [J].Mechanical and Electrical Information,2016(24):92-93.

(責任編輯：李 磊)

Research on Fault Diagnosis of Chemical Process Based on Improved PCA Method

DU Hailian1, MIAO Shiyu2, DU Wenxia1, LIU Xiaoliang3

(1. College of Career Technology, Hebei Normal University, Shijiazhuang, Hebei 050024, China;2. School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China;3. Sifang College, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 051132, China)

In order to further improve the accuracy and persuasiveness of the fault diagnosis of complex system in chemical production, data of the system at normal working state and failure state were collected, and the improved principal component analysis (PCA) algorithm was used to determine whether there was fault in the system. Based on the traditional PCA, the improved PCA algorithm decomposed the squared prediction error (SPE) statistic into principal-component-related variable residual (PVR) statistic and common variable residual (CVR) statistic, and it was then cooperated with Hotelling’sT2statistics to diagnose fault of the system so that the diagnostic results were more accurate and the production process was more safe. Finally, the improved PCA method was applied in Tennessee Eastman process. The results show that this method, being able to identify the normal mode state and fault state more accurately, is an effective method of fault analysis and diagnosis.

PCA； fault diagnosis； production safety

2017-03-11

國家自然科學基金項目(61673160,60974063,61175059)；河北省自然科學基金項目(F2014205115)；河北省教育廳課題(ZD2016053)

杜海蓮(1978—)，女，河北保定人，副教授，主要從事故障診斷方面的研究.E-mail： duhailian@126.com 杜文霞(1973—)，女，河北衡水人，副教授，博士，主要從事智能監測與故障診斷的研究，本文通信作者. E-mail:dwx20040513@163.com

TP206

A

1672-3767(2017)05-0016-07

10.16452/j.cnki.sdkjzk.2017.05.003