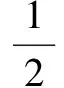妙用整體法 優(yōu)化高中物理解題教學(xué)

沈宇峰

(江蘇省吳江中學(xué),江蘇 蘇州 215200)

?

妙用整體法 優(yōu)化高中物理解題教學(xué)

沈宇峰

(江蘇省吳江中學(xué),江蘇 蘇州 215200)

在高中物理中，整體法是一個(gè)重要的解題思路，可以省略中間量的計(jì)算步驟，提升解題效率.本文在簡要分析整體法的內(nèi)涵以及結(jié)合物理力學(xué)分析其具體的解題思路的基礎(chǔ)上，結(jié)合具體教學(xué)案例，探討了整體法在研究對象、物理過程以及對象和過程的綜合整體化三方面的具體運(yùn)用，以期能幫助學(xué)生在解題過程中正確使用整體法，進(jìn)而提升解題能力.

高中物理；整體法；解題；運(yùn)用

在高中物理中，整體法是一個(gè)重要的解題思路，這種思維方式是將所涉及的多個(gè)過程、多個(gè)物體視為一個(gè)研究整體予以分析，省去了繁瑣的中間量，降低了學(xué)生的出錯(cuò)率.但是，整體法的運(yùn)用，需要仔細(xì)審題，注重方法使用的判斷標(biāo)準(zhǔn)，才能準(zhǔn)確發(fā)揮整體法解題技巧的實(shí)效性，而研究對象的選取正是解題過程中的重點(diǎn)，也是難點(diǎn)所在，如何幫助學(xué)生在解題過程中正確使用整體法，進(jìn)而提升解題能力呢？本文從如下幾方面進(jìn)行了有益探索，現(xiàn)與同行共同探討如下：

一、認(rèn)識(shí)整體法，剖析其內(nèi)涵

所謂整體法，是指物理過程的實(shí)質(zhì)在確保不會(huì)受到影響的前提下，將整個(gè)過程或多體系統(tǒng)看作為一個(gè)整體，可以忽視系統(tǒng)內(nèi)部的個(gè)體間的運(yùn)動(dòng)效果和系統(tǒng)內(nèi)部的受力情況，從整體層面把握問題，可以省略中間量的計(jì)算步驟，從而準(zhǔn)確快速的得出問題的計(jì)算結(jié)果，這樣的解題方法在高中物理中較為常見.比如，動(dòng)能定理、機(jī)械能守恒定律、動(dòng)量守恒定律、功能定律等都可以整體過程考慮，不必拘泥于局部，在整體上把握問題，可以靈活地解決問題，有效優(yōu)化解題過程.

在解題中使用整體法，不僅可以培養(yǎng)學(xué)生的整體思維，使學(xué)生能夠著眼于問題的整體結(jié)構(gòu)進(jìn)行思考問題，從整體上分析問題，也能幫助學(xué)生靈活地解決物理問題，提高學(xué)生分析和解決實(shí)際問題的能力.

二、結(jié)合物理力學(xué)，理順解題思路

首先，運(yùn)用整體法解題要確定研究對象，待研究的整體對象的確定至關(guān)重要，不僅不能違背原有的物理內(nèi)涵，同時(shí)也要結(jié)合題目中的具體情境科學(xué)選擇待研究對象.其次是對選取的研究對象進(jìn)行受力分析，這是重點(diǎn)也是難點(diǎn)，不論系統(tǒng)內(nèi)各物體是分離狀態(tài)還是聯(lián)結(jié)狀態(tài)，只要不考慮其內(nèi)部的相互作用，只需分析整體所受外力的情況下，那么就能將這個(gè)多體系統(tǒng)看成是一個(gè)整體.最后是根據(jù)平衡條件、牛頓第二定律等已知條件列方程，簡單算法.在大多數(shù)的題目中，都以求出沿某個(gè)方向的合外力、整體的加速度等情況，是很多題目的必須手段.

三、分析具體案例，內(nèi)化解題運(yùn)用

1.研究對象的整體法

案例1 如圖1所示，直角支架AOB中，AO表面粗糙，OB表面光滑，將AO水平放置，OB豎直向下.將一質(zhì)量為m的小環(huán)P套于AO上，相同質(zhì)量的小環(huán)Q套于OB上，將一根不可伸長、質(zhì)量可忽略的細(xì)繩將兩環(huán)相連，并在某一位置平衡.現(xiàn)將P環(huán)向左移一小段距離，兩環(huán)再次達(dá)到平衡，請判斷：移動(dòng)后的平衡狀態(tài)和原來的相比較，AO桿對P環(huán)的支持力N不變，但細(xì)繩上的拉力T變小，是否正確？

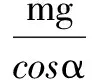
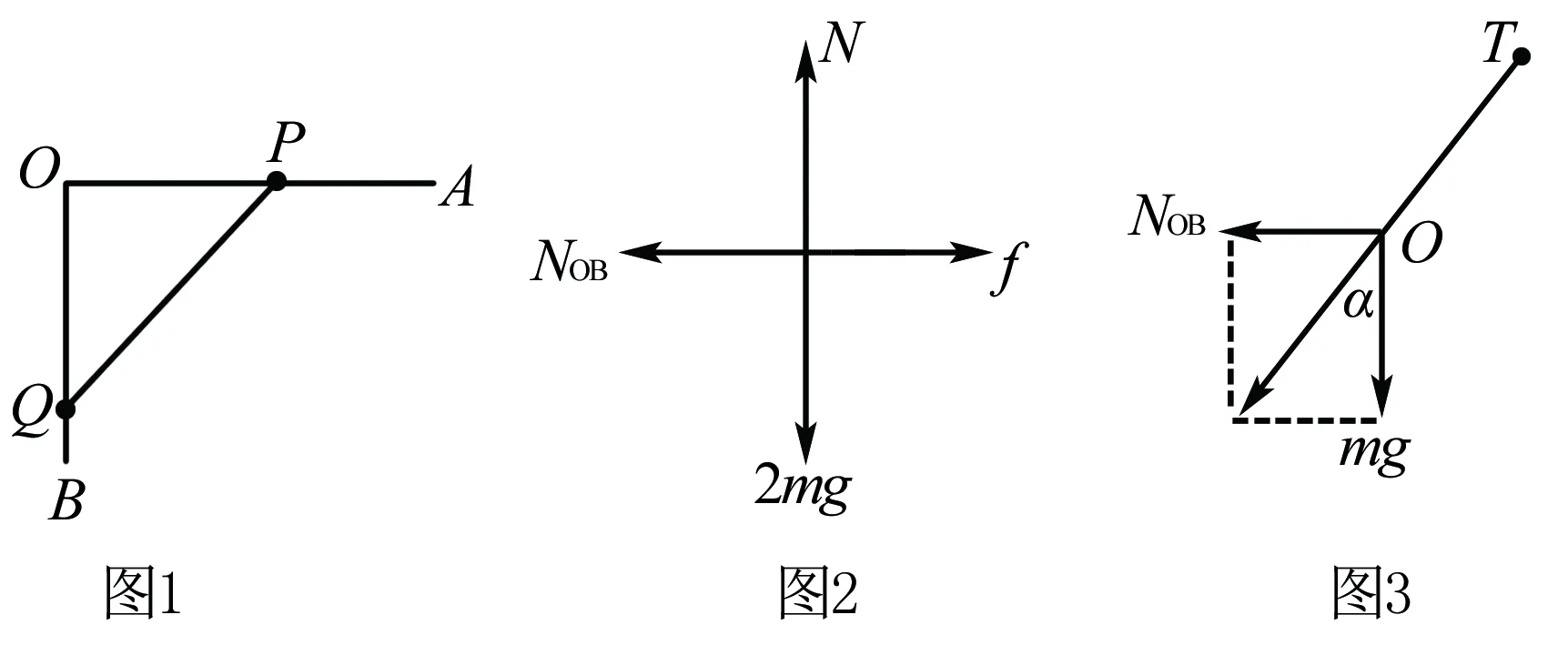
可見，靈活選擇研究對象是關(guān)鍵.在本題中，涉及的物體都處于靜止?fàn)顟B(tài)，且不涉及物體間相互作用，故而研究分析時(shí)可以看作是一個(gè)整體，簡化問題.但是，只有在研究系統(tǒng)外力的情況下，才能運(yùn)用整體法求解，

2.研究物理過程的整體法

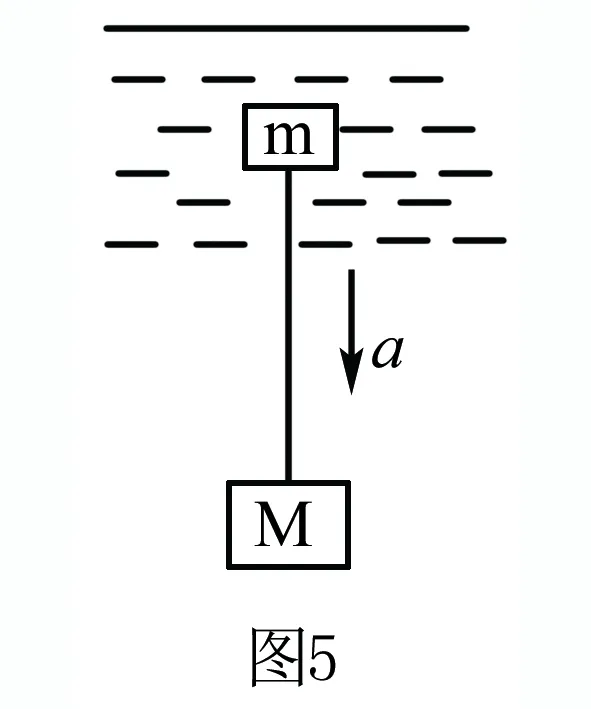
案例2 如圖4所示，在一地面上，固定一光滑平臺(tái)，長度為L.在該平臺(tái)的中央放置彼此相接觸的物體A和B.物體A的上表面是半圓形軌道，半徑為R，且R

3.研究對象和研究過程的綜合整體化分析

案例3 如圖5所示，有一質(zhì)量為m的木塊下面用一根細(xì)線連接一鐵塊，鐵塊質(zhì)量為M，一起浸沒在水中，初期都停止，之后開始以α的加速度在水中下沉，經(jīng)過時(shí)間t1以后，細(xì)線斷裂，木塊和金屬塊繼續(xù)下沉，又經(jīng)過時(shí)間t2以后木塊停止下沉，求此時(shí)金屬塊的速度.

案例分析 木塊和鐵塊一起以加速度α下沉，經(jīng)時(shí)間t1以后兩者獲得一定的速度.細(xì)線斷裂后，鐵塊向下作加速運(yùn)動(dòng)，木塊則向下作減速運(yùn)動(dòng).根據(jù)受力情況和運(yùn)動(dòng)變化的特征，即可根據(jù)力與運(yùn)動(dòng)變化的關(guān)系求解.首先將木塊和鐵塊視作一整體，其所受外力恒為總重力與總浮

力，即F=(m+M)α.經(jīng)過時(shí)間t1以后，細(xì)線斷開，但系統(tǒng)所受的合力沒有發(fā)生變化.以物體的過程作為研究對象，系統(tǒng)從開始運(yùn)動(dòng)到木塊停止，整個(gè)過程中系統(tǒng)所受的沖量為(m+M)α(t1+t2).解題過程中，設(shè)所求的鐵塊速度為V，整個(gè)系統(tǒng)動(dòng)量的增量即為MV，以整個(gè)系統(tǒng)為演技對象，運(yùn)用動(dòng)量定量，可得(m+M)α(t1+t2)=MV.

相比之下，這道題目如果運(yùn)用功與動(dòng)能變化的關(guān)系，或者根據(jù)牛頓第二定律進(jìn)行求解，雖然也能計(jì)算出來，但遠(yuǎn)不如整體法方便、快捷.

綜上所述，整體法解題技巧在高中物理解題過程中發(fā)揮著重要的作用.在平時(shí)的解題教學(xué)中，教師應(yīng)有意識(shí)地滲透整體法技巧的運(yùn)用，巧妙地選擇研究對象與研究過程，為學(xué)生提供明確的解題思路.這不僅能幫助學(xué)生合理的簡化計(jì)算過程，更能培養(yǎng)學(xué)生的學(xué)科素養(yǎng).

[1]王力.議高中物理力學(xué)解題中整體法的運(yùn)用[J].新課程導(dǎo)學(xué),2012(08):66.

[2]杜鑫.高中物理的隔離法與整體法研究[J].教育,2017(01):246.

[責(zé)任編輯：閆久毅]

2017-05-01

沈宇峰(1979.11-)，男，江蘇吳江人，大學(xué)本科，中學(xué)一級(jí)教師，從事中學(xué)物理教育研究.

G632

B

1008-0333(2017)18-0049-02