高考易錯題自測卷
——數列

江蘇 呂從軍 李 凱

高考易錯題自測卷
——數列

江蘇 呂從軍 李 凱

一、選擇題

1．已知Sn是數列｛an｝的前n項和且有Sn＝an－1（a≠0且為常數），那么數列｛an｝是 （ ）

A．等差數列

B．等比數列

C．既不是等差數列也不是等比數列

D．可能是等差數列，也可能是等比數列

2．已知數列an＝n2－tn＋2在（n≥2，n∈N＊）上是遞增數列，則實數t的取值范圍是 （ ）

A．［－5，5］ B．（－5，＋∞）

C．（－∞，5） D．（－5，5）

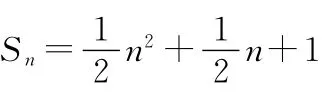
4．已知等比數列｛an｝中，a2＝1，則S3的取值范圍是（ ）

A．（－∞，－1］ B．［3，∞）

C．（－∞，－1］∪［3，∞）D．（－∞，1）∪（3，＋∞）

5．已知數列｛an｝的前n項和Sn＝n（n－40），則下列判斷中正確的是 （ ）

A．a19＞0，a21＜0 B．a20＞0，a21＜0

C．a19＜0，a21＞0 D．a19＜0，a20＞0

6．Sn是數列｛an｝的前n項和，若Sn＝3n－2，則an＝（ ）

7．已知等比數列｛an｝為遞增數列．若a1＞0，且2（an＋an＋2）＝5an＋1，則數列｛an｝的公比q＝ （ ）

A．1 B．2

C．3 D．4

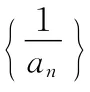
9．若數列｛an｝的前n項和，則數列｛nan｝中數值最小的項是第（ ）項．

A．5 B．4

C．3 D．2

10．已知等比數列｛an｝的公比為q，前n項和為Sn，已知2S5、S10、S20－S10構成等比數列，則S5、S15、S10構成的數列是 （ ）

A．等差數列

B．等比數列

C．既不是等差數列也不是等比數列

D．公比q≠1時構成等差數列，q＝1時不構成等差數列

二、填空題

12．已知數列｛an｝，a1＝a2＝1，an＝an－1＋2（n≥3，），則an＝________．

13．已知數列｛an｝中，a1＝1，an＋1＝2an＋3，則an＝________．

15．已知數列｛an｝滿足：），an＋1＝若a6＝1，則m所有可能的取值個數為_______．

18．已知等差數列｛an｝的前m項，前2m項，前3m項的和分別為Sm，S2m，S3m，若Sm＝30，S2m＝90，則S3m＝________．

19．在等差數列｛an｝中，an＝3n－31，記bn＝｜an｜，則數列｛bn｝的前30項和為_______．

20．設等比數列｛an｝的公比為q，前n項和，則q的取值范圍是_______．

【參考答案與提示】

1．D 【解析】由Sn－Sn－1＝（a－1）an－1（n≥2），當a≠1時，｛an｝是等比數列，當a＝1時，｛an｝是等差數列，故選D．

【易錯警示】忽視a＝1時，｛an｝是等差數列，錯選B．

2．C 【解析】依題意a2＜a3，即4－2t＋2＜9－3t＋2，故t＜5．

【易錯警示】不注意n的取值范圍，用a1＜a2列不等式求實數t的取值范圍．

當n≥2時，

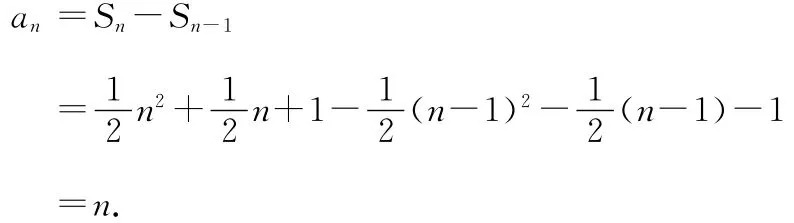
【易錯警示】使用公式an＝Sn－Sn－1時如果不注意n≥2，會錯選A．

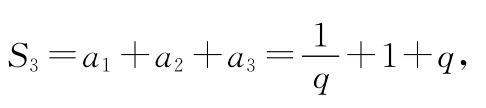
①當q＞0時S3≥3當且僅當q＝1時取等號；

②當q＜0時S3≤－1當且僅當q＝－1時取等號．

所以S3的取值范圍為（－∞，－1］∪［3，＋∞）．

【易錯警示】忽視q＞0或q＜0中一種情況，致使答案不全面．

5．C 【解析】當n＝1時，a1＝S1＝－39；當n≥2時，an＝Sn－Sn－1＝n（n－40）－（n－1）（n－41）＝2n－41．將n＝1代入滿足上式．綜上有an＝2n－41．所以a19＝2×19－41＝－3＜0，a20＝2×20－41＝－1＜0，a21＝2×21－41＝1＞0．故選C．

【易錯警示】求an去括號時出錯．

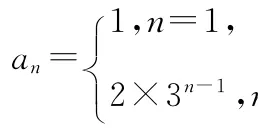
【易錯警示】當n≥2時求出an后不注意驗證a1是否滿足條件．

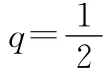
又數列｛an｝為遞增數列，且a1＞0，所以q＝2．【易錯警示】忽視數列｛an｝為遞增數列．

1＋q3＝9，所以q＝2．

所以前5項和

9．C 【解析】因為Sn＝n2－10n），所以｛an｝為等差數列，an＝2n－11，所以nan＝2n2－11n＝2，其中數值最小的項應是最靠近對稱軸的項，即n＝3，第3項是數列｛nan｝中數值最小的項．

【易錯警示】求最小值時忽視n為正整數．

10．D 【解析】應用分類討論求解：

①當q＝1時，S5＝5a1，S15＝15a1，S10＝10a1，

此時S5＋S10＝15a1，2S15＝30a1，

所以S5＋S10≠2S15，

所以S5、S15、S10不構成等差數列．

②當q≠1時，依題意，2S5、S10、S20－S10構成等比數列，所以

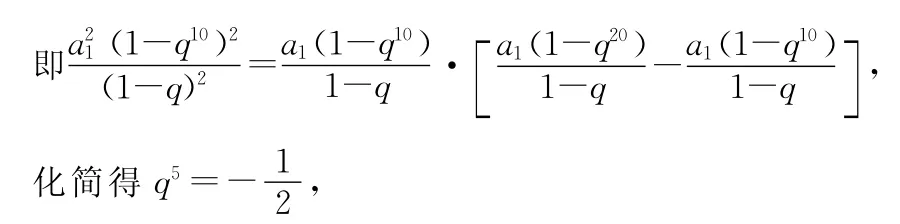
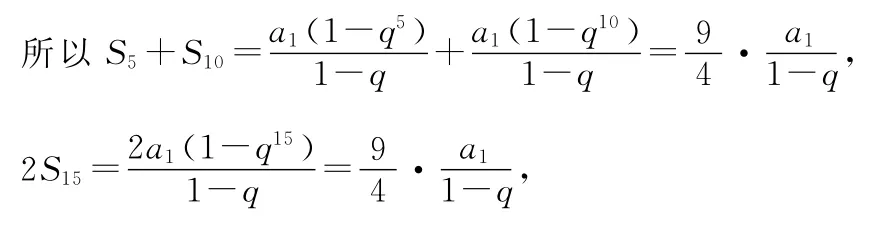
所以S5、S15、S10構成等差數列．

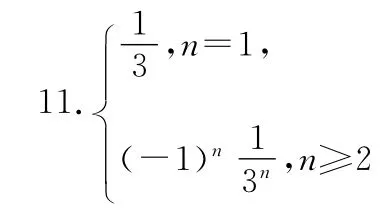
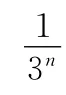
所以an＝3＋2（n－3）＝2n－3．

當n＝2時，a2＝2×2－3＝1也適合，

【易錯警示】不注意題目中n的取值范圍，結論錯寫成an＝2n－3．

13．an＝2n＋1－3【解析】設遞推公式an＋1＝ 2an＋3可以轉化為an＋1－t＝2（an－t），即an＋1＝2an－t，則t＝－3，故遞推公式為an＋1＋3＝2（an＋3），所以2．所以｛an＋3｝是以a1＋3＝4為首項，2為公比的等比數列，則an＋3＝4×2n－1＝2n＋1，所以an＝2n＋1－3．

【易錯警示】不能通過an＋1＝2an＋3這一條件構造等比數列｛an＋3｝．

14．5【解析】由等差數列的前n項和及等差中項，可得

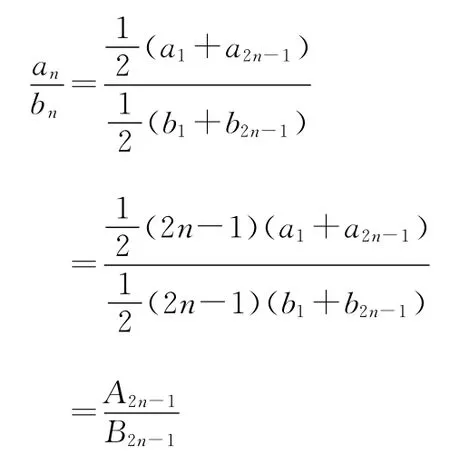
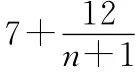
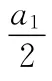
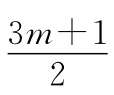
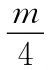
【易錯警示】分段函數的單調性判斷出錯，以致列出的不等式組不全面．

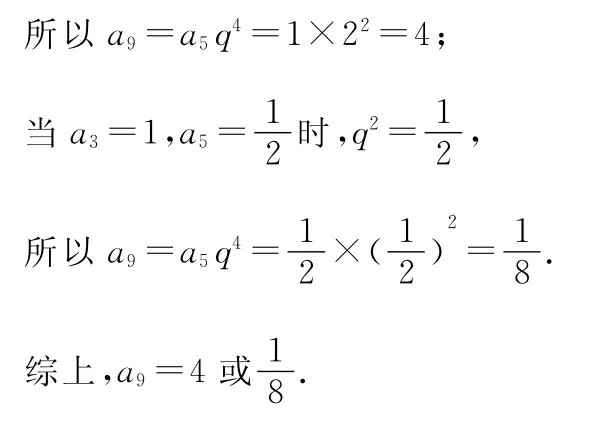
【易錯警示】a3、a5的取值注意不要漏掉一種情況．

18．180【解析】設數列的公差為d，

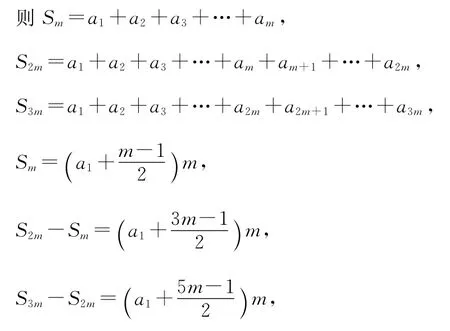
所以Sm，S2m－Sm，S3m－S2m是公差為m2d的等差數列，

所以2（S2m－Sm）＝Sm＋S3m－S2m．

即2×（90－30）＝30＋S3m－90，所以S3m＝180．

【易錯警示】不會利用等差數列的性質判斷Sm，S2m－Sm，S3m－S2m成等差數列，

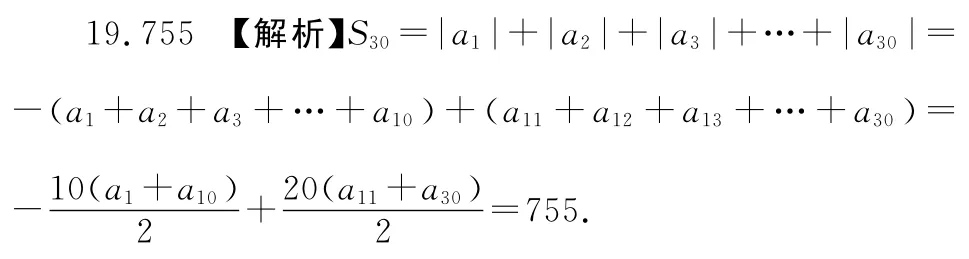
【易錯警示】忽視絕對值的意義，認為bn＝an．

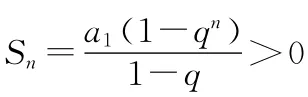
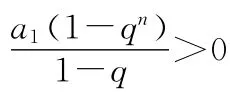
（作者單位：江蘇省贛榆縣海頭高級中學，江蘇省啟東市呂四中學）