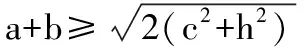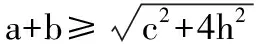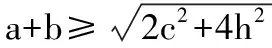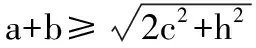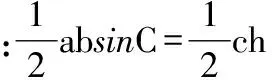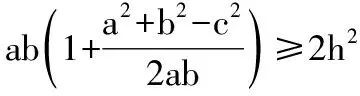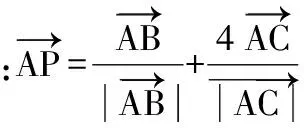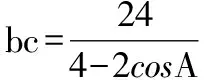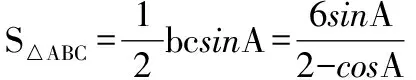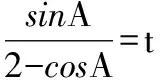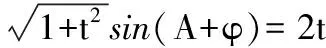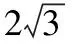三角形中的綜合問題求解策略
廣東 袁長林
(作者單位:廣東省珠海市第一中學)
三角形中的綜合問題求解策略

學生在小學就已經接觸到三角形,在初中學習了三角形的幾何性質,在高中又將該內容拓展到解三角形.從最初對圖形結構的初步了解,到定性分析,再到定量計算,三角形中的問題層出不窮,近年來受到全國高考命題老師的青睞.對于高考中的三角形綜合問題,很多學生不知如何理解問題,更不知從何下手.本文將解讀三角形中的經典的綜合問題的常見求解策略,為高三學子的復習保駕護航.
一、平面幾何背景
問題本身是平幾形式的背景:三角形、四邊形等,被輔以包裝,知識聯系到向量等內容,往往考查的是工具性的平幾運算.
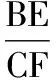
【解析】此題背景是正弦定理形式,可考慮轉化為邊的關系,進而用特殊的邊或一般形式的邊關系,依托中線的平面幾何背景或余弦定理朝目標轉化,建立函數關系,達到求解問題的目的,基于以上思路產生以下兩種解法:
解法一:由3sinC=2sinB,聯系正弦定理不妨設AB=2,則AC=3,1 又因為4BE2+9=2(4+BC2),4FC2+4=2(9+BC2), 解法二:設AB=2t,則AC=3t, 在△ACF中同理可得:CF2=10t2-6t2cosA, 其中x=cosA∈(-1,1). 兩種方法相比較,方法一融入了平面幾何關系,方法二的工具性更加明顯,本質上來說是一致的,都體現了平面幾何的工具性. 從數據本身分析,條件中的部分關系是解析幾何化的背景,因此可以聯系到圓、橢圓等曲線,利用二次曲線的幾何特征去解決問題. 【解析】a+c=4明顯是一橢圓背景,由此打開思路. 解法:∵a+c=4,∴|BA|+|BC|=4>|AC|. 故點B的軌跡是以A、C為焦點的橢圓,當△ABC面積最大時,點B在短軸的端點上, ∴(2-cosA)cosA=sin2A, 做完本題,意猶未盡,趁熱鞏固下面問題: 【變式1】(2013江蘇省數學時代杯競賽題) 在三角形ABC中,點E、F分別是邊AB、AC的中點,已知CE=6,BF=9,則三角形ABC面積的最大值為________. 對動態圖形的認識還可以從極端方向入手,從極端(特殊)到一般的思維模式會打開一個又一個懸疑,直至問題解決. 【例3】(全國卷2015年16題,壓軸填空題)在平面四邊形ABCD中,∠A=∠B=∠C=75°,BC=2,則AB的取值范圍是________. 【解析】平面四邊形是動態的,通常我們可以考慮將四邊形問題轉化為三角形處理,因此產生了如下解法: 延長BA、CD交于點E.∵∠B=∠C=75°,∴△EBC為等腰三角形,∠E=30°. 極端原理的處理方式也很廣泛,從幾何角度:平面多邊形,空間幾何體;從代數角度:不等式與等式,函數與方程等. 對于極端原理這一處理方式,你會使用了嗎? 【變式】在平面四邊形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=2,則線段AC長度的取值范圍是________. 四種數學思想是解決數學問題的法寶,應該說數學思想是數學核心素養的一部分,在解題中善于引導學生去從思想上思考,尋求問題的突破口. 【解析】既然問題是求最值,說明三角形是動態變化的,因此需要尋求變化中的變量描述,考慮到邊長關系,可以引入長度,考慮線段AB=2,或者可以引入坐標,通過代數途徑需求解決問題的方法,有以下兩種解法: 比較兩種解法,明顯方法二占優勢,計算量小,處理簡潔,究其原因挖掘了解析法——坐標化,其實這種問題屢見不鮮,因為其幾何背景是阿波羅尼斯圓,多次在高考題中出現,值得高三教師關注. 有些問題本身帶有朦朧色彩,即有一定的迷惑性,如果考慮不周會陷入誤區,這也算是思維嚴謹性訓練吧!請看下面問題. 【解析】條件簡單,若做直接運算,利用內角和及誘導公式有如下解法: 如果單純地考慮問題,題目算解決了,但兩個答案總感覺有點不對勁,問題出現在哪里呢?想不通,那就嘗試算一下sinC吧,可能有人問為什么呢?至少和問題有關吧,這是其一,其二是它是正數,那就繼續: 為什么出現增根呢?這時我們仔細排查,發現三角形中有大小關系,漸漸地認識到:∵sinA 想一想:你能否做出幾何方面的解釋? 有些問題綜合性很強,很大程度上體現在運算上,需要抽絲撥繭式地分析運算的途徑與方式,從而培養靈活的分析問題與解決問題的能力. 【例6】在三角形ABC中,a,b,c分別為三角A,B,C的對邊,若過點C作垂直于AB的垂線CD,且CD=h,則下列給出的關于a,b,c,h的不等式中正確的是 ( ) 【解析】本題看似眼花繚亂,無從下手,考慮到h的問題,可以聯系三角形的面積.問題是角的處理,考慮最終是求邊的關系,那就大膽使用余弦作為突破口,順藤摸瓜,產生了如下解法: ?a2b2(1-cosC)(1+cosC)=(a2+b2-2abcosC)·h2 ?a2b2(1-cosC)(1+cosC)≥(2ab-2abcosC)·h2 ?(a+b)2≥c2+4h2. 確實,本題需要過強的三角變形與計算能力,還有化等為不等關系,借助于基本不等式這一工具,不過,仔細斟酌,似乎想起來什么,課本中有一道復習參考題也是類似的變形:證明海倫公式!(人教A版,第20頁B組第2題第一問) 應該說,源于課本,超于課本,是一種命題的很好思路. 【變式】 (1)在三角形ABC中,點M為BC的中點,且BC=4,AM=c-b,求三角形ABC的面積的最大值. 【解析】(1)中線的問題可以考慮建立向量或平行四邊形之等價關系,如下:2(b2+c2)=(2c-2b)2+16?b2+c2-4bc+8=0,下面怎么辦呢? 看問題,面積可以聯系到角,試一下: (2)考慮垂直關系使用坐標系容易入手,又有長度關系,那就嘗試一下: (作者單位:廣東省珠海市第一中學)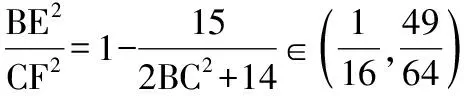
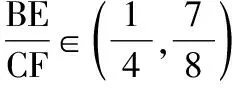
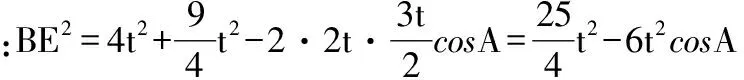
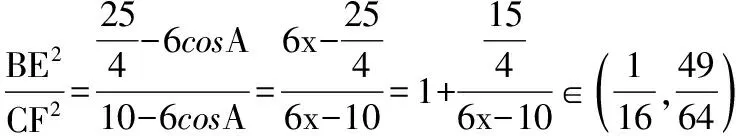
二、解析幾何化背景
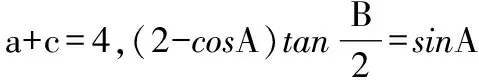
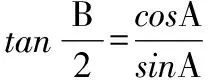
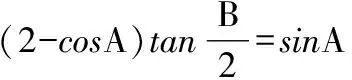

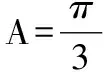

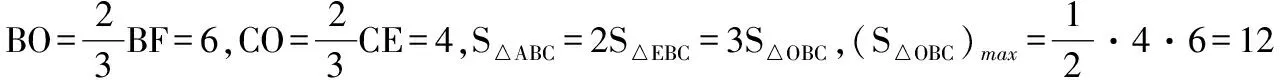
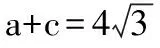
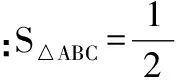
三、極端原理
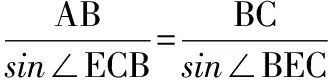
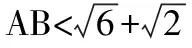
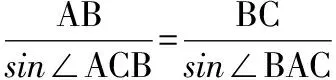
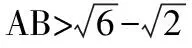

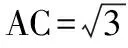
四、思想化處理
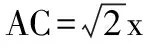
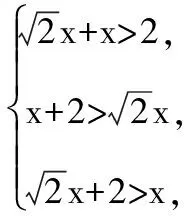
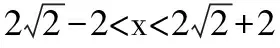
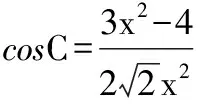
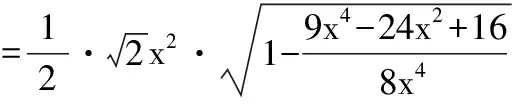
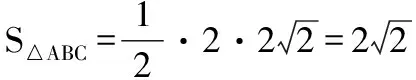
五、易錯性問題
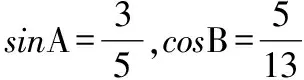
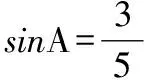
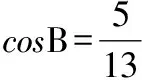
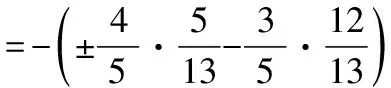

六、綜合運算問題