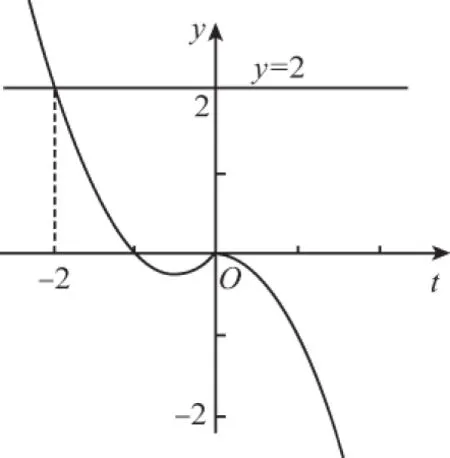
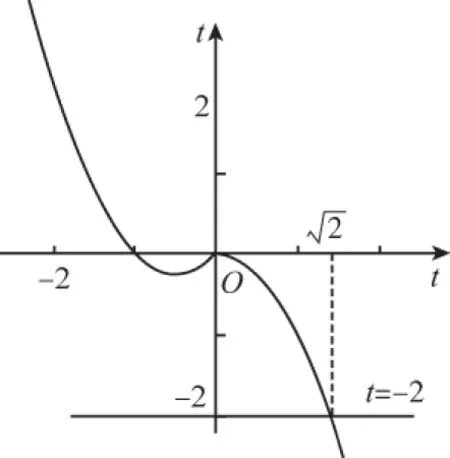
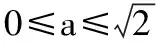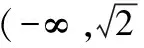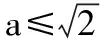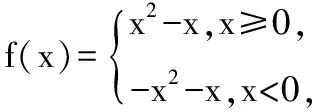復合函數的零點問題
福建 黃清波
(作者單位:福建省南安市國光第二中學)
復合函數的零點問題

復合函數的零點問題是高考和模擬考試中的一個熱點問題,備受命題人青睞.復合函數涉及內外兩層函數,這本來就是學生的一個難點,問題的解決往往涵蓋函數方程、數形結合、分類討論和化歸轉化四種重要數學思想,所以復合函數零點問題具有關系復雜、綜合性強、難度大等特點,對考生的思維能力、運算能力和耐心細致、處變不驚的心理素質都有較高的要求,可以說是小題中的大題.這類問題大多作為選擇題或填空題的最后一題把關壓軸. 本文以福建省廈門市2016屆普通中學高中畢業班質量檢查文科卷第12題為例對復合函數零點問題的解法進行剖析,希望對大家有所幫助.
( )
A.(-1,0)∪(0,+∞) B.(-∞,0)∪(0,1)
C.(-1,0)∪(0,1) D.(-∞,-1)∪(1,+∞)
【命題意圖】本題主要考查函數與方程的應用,利用換元法將條件轉化為兩個函數的交點個數問題是解決本題的關鍵.利用數形結合以及分類討論的數學思想,綜合性較強,難度較大,學生得分率低.
一、解法探究
1.直譯法
【解法1】由選項知k≠0.當k>0時,
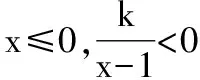
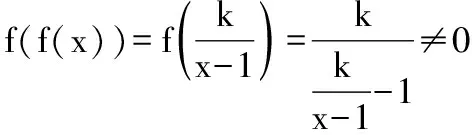
所以f(f(x))=0無解.
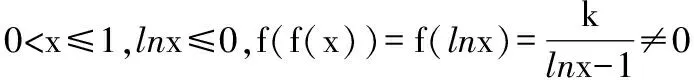
所以f(f(x))=0無解.
若x>1,lnx>0,f(f(x))=f(lnx)=ln(lnx),
則f(f(x))=0,得x=e.符合題意.
當k<0時,
若x>1,lnx>0,f(f(x))=f(lnx)=ln(lnx),
則f(f(x))=0,得x=e.
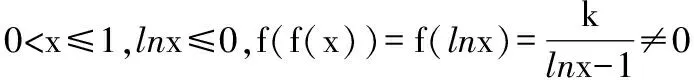
所以f(f(x))=0無解.
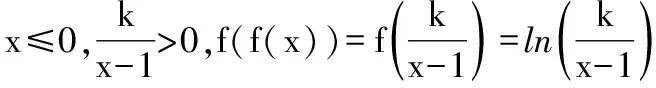
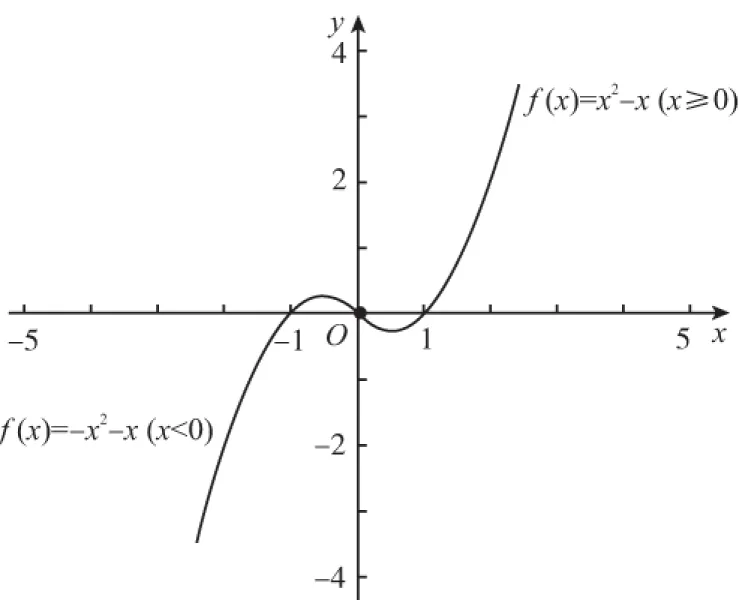
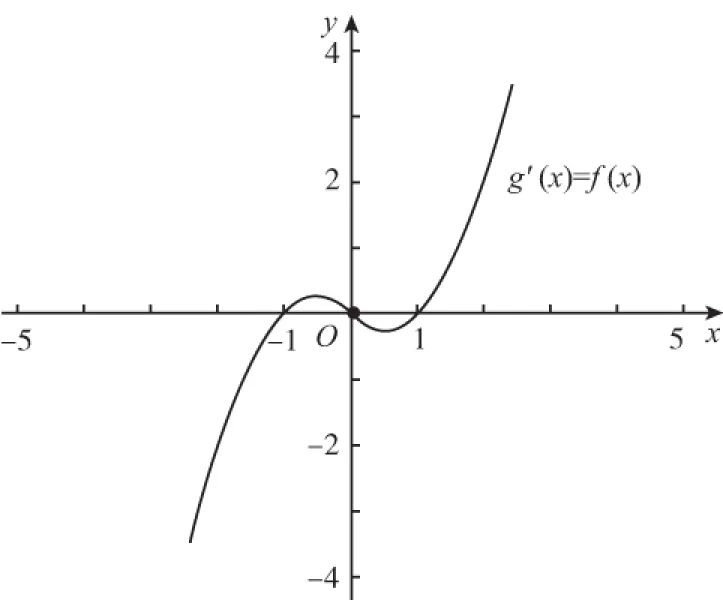
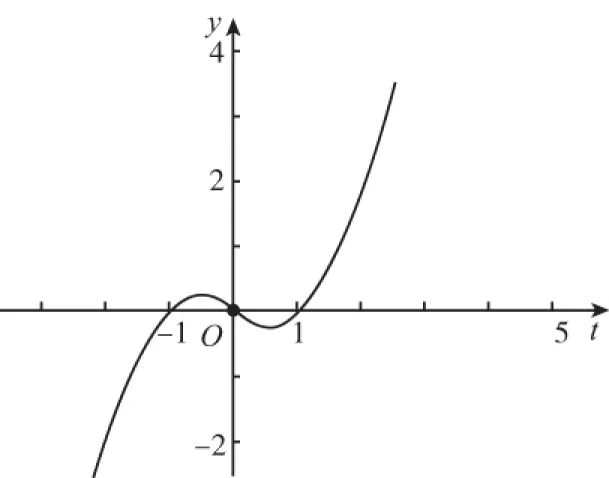
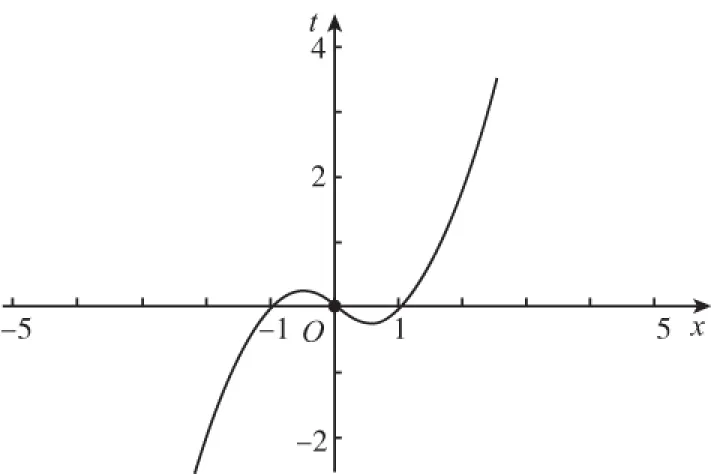
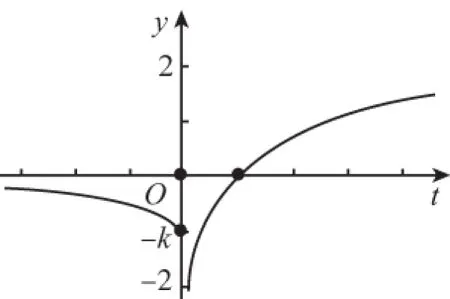
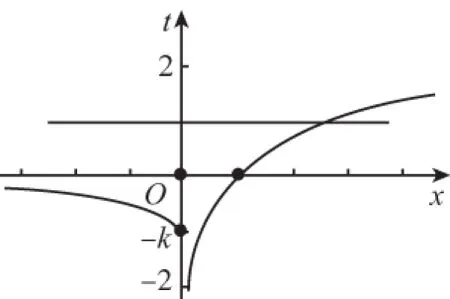
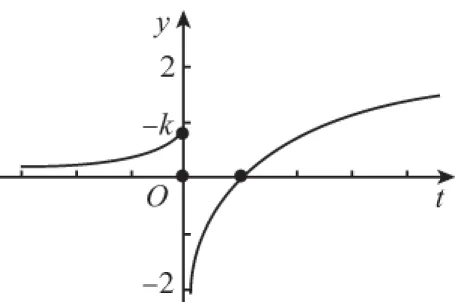
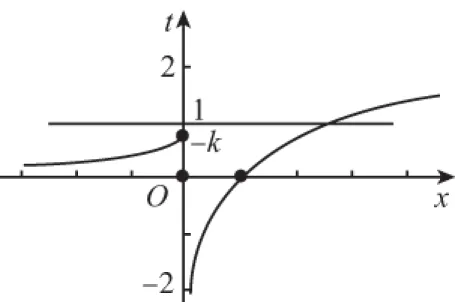
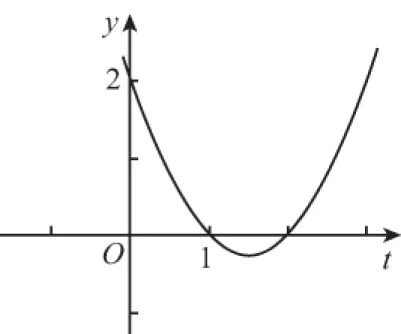
又因為關于x的方程f(f(x))=0有且只有一個實數解,則x≤0時,f(f(x))=0無解.則-1 綜上,實數k的取值范圍是(-1,0)∪(0,+∞),故選 A. 2.換元法 【解法2】由選項知k≠0. 設t=f(x),則由f(f(x))=0,得f(t)=0. 若關于x的方程f(f(x))=0有且只有一個實數解,則其等價為f(x)=1有唯一解. 又當x>0時,f(x)=lnx=1,得x=e. 此時只要滿足-k<1,即-1 綜上,實數k的取值范圍是(-1,0)∪(0,+∞),故選A. 3.圖象法 【解法3】由選項知k≠0. 當k>0時,分別作出y=f(t),t=f(x)的圖象. 如圖1,f(t)=0,得唯一解t=1.如圖2,f(x)=1,得唯一解x=e.即k>0符合題意. 圖1 圖2 當k<0時,分別作出y=f(t),t=f(x)的圖象. 如圖3,f(t)=0,得唯一解t=1.如圖4,若f(x)=1有唯一解,只需-k<1,即-1 圖3 圖4 綜上,實數k的取值范圍是(-1,0)∪(0,+∞),故選A. 【點評】解法1(直譯法)采用直譯的方式確定函數解析式,繼而轉化為解方程問題,思路自然,貼近學生最近發展區.但分類復雜,計算煩瑣,復雜題目不易求出函數解析式.解法2(換元法)將f(x)看成一個整體t,利用t的“橋梁”作用解方程f(t)=0和方程f(x)=1.通過分解,使問題載體保持簡單,步步為營直到順利解決,體現化歸與轉化思想方法的威力,是通性通法,也是命題意圖.解法3(圖象法)將數形結合與推理論證結合起來,問題一目了然,結果不言自明,達到“秒殺”的效果. 當然,高考是限時的選拔性考試,考生必須有爭分奪秒的速度意識.所以我們提倡“小題巧做”.本題也可考慮采用特殊值法,當k=1時,符合題意,直接就排除B,C,D. 【解析】(換元法)設t=h(x),則由f(h(x))=0,得f(t)=0.即t2-3t+2=0,解得t1=1或t2=2. (1)當t=1時,h(x)=1. (2)當t=2時,h(x)=2. 【解析】(圖象法)分別作出y=f(t),t=h(x)的圖象. 圖5 圖6 如圖,若f(h(x))有5個零點,對于圖6則必須存在t1=1且t2>0(t1≠t2).即方程t2+bt+2=0必須有兩個不等實根,且一根等于1,另一根大于0.由韋達定理,t1·t2=2,得t2=2. 【解法1】(換元法)令t=f(a),則由f(f(a))≤2轉化為f(t)≤2. 當t≥0時,f(t)=-t2≤2,解得t≥0; 當t<0時,f(t)=t2+t≤2,解得-2≤t<0. 故不等式f(t)≤2的解集為[-2,+∞). 下面解不等式f(a)≥-2. 當a<0時,f(a)=a2+a≥-2,解得a<0. 【解法2】(圖象法)分別作出y=f(t),t=f(a)的圖象. 圖7 圖8 如圖7,f(t)≤2,得t≥-2. 【變式】已知函數f(x)是定義在R上的奇函數,當x≥0時,f(x)=x(x-1). (Ⅰ)求函數f(x)的解析式,并畫出函數f(x)的圖象; (Ⅱ)設函數g(x)的導函數g′(x)=f(x),求函數g(x)的極值點; (Ⅲ)設函數h(x)=f(f(x)),求函數y=h(x)的零點個數. 【命題意圖】此題主要考查二次函數、分段函數、復合函數、導數、函數奇偶性、單調性、極值點、零點等基礎知識,考查推理論證能力、運算求解能力,考查函數與方程思想、分類與整合思想、化歸與轉化思想、數形結合思想等.其中第(Ⅲ)問h(x)=f(f(x))的解析式不好求,且次數將達到4次,較難判斷零點,會導致不少學生放棄.須對函數h(x)的重新構造、轉化、分析.對學生要求較高. 【解析】(Ⅰ)因為函數f(x)是定義在R上的奇函數, 令x<0,則-x>0. 有f(x)=-f(-x)=-[(-x)(-x-1)]=-x2-x. 作出函數f(x)的圖象的圖象,如圖9. 圖9 (Ⅱ)由(Ⅰ)得函數g(x)的導函數g′(x)的圖象,如圖10. 圖10 由圖可知,x∈(-∞,-1),g′(x)<0;x∈(-1,0),g′(x)>0;x∈(0,1),g′(x)<0;x∈(1,+∞),g′(x)>0; 由極值點的定義可知,函數g(x)的極小值點為x=-1和x=1,極大值點為x=0. (Ⅲ)函數h(x)的零點為f(f(x))=0的根. 設t=f(x),則f(t)=0. 分別作出y=f(t)、t=f(x)的圖象,如圖11,12. 圖11 圖12 由圖11易得f(t)=0有三個根,分別為t1=-1,t2=0,t3=1. 對應圖12,當t1=-1時,t=f(x)=-1有一解, 即對應y=h(x)有1個零點, 當t1=0時,t=f(x)=0有三解, 即對應y=h(x)有3個零點, 當t1=1時,t=f(x)=1有一解, 即對應y=h(x)有1個零點. 綜上,函數y=h(x)有5個零點. (作者單位:福建省南安市國光第二中學)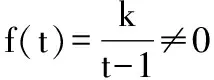
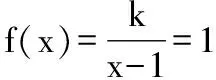
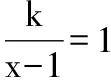
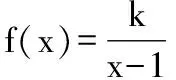
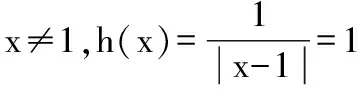
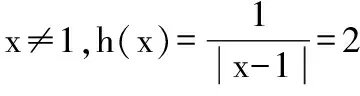
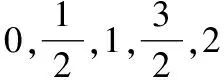

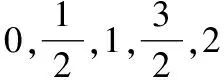
二、高考鏈接