二輪復習要重視教材
——以平面向量數量積為例

浙江 劉志昌 李承法

(作者單位：浙江省開化中學)

二輪復習要重視教材
——以平面向量數量積為例

二輪復習要重視教材，能幫助同學們跳出題海、高效復習的唯有教材.平面向量的數量積是每年高考的重點和熱點內容，且常與三角函數、數列、解三角形、解析幾何等交匯命題，常考常新.解答此類問題或轉化為代數運算，或利用其幾何意義，其轉化途徑主要是利用平面向量數量積的公式和性質，而這些解題思路，其實就在教材中！

一、橫看成嶺側成峰，遠近高低各不同——重視平面向量數量積之投影形式

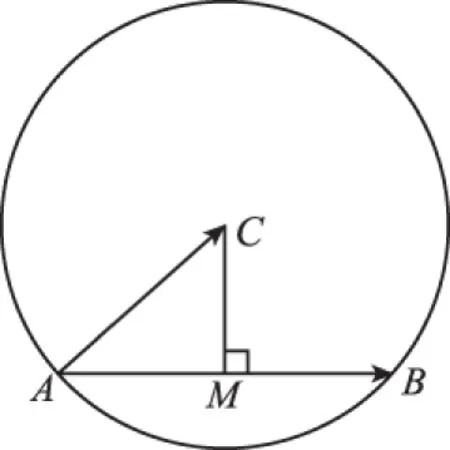
圖1

( )

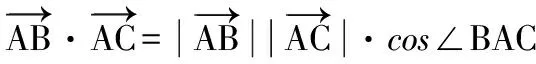
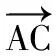
A.只與圓C的半徑有關

B.只與弦AB的長度有關

C.既與圓C的半徑有關，又與弦AB的長度有關

D.是與圓C的半徑和弦AB的長度均無關的定值

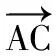
【評注】本例是教材習題的改編，而教材中的這道習題本身就是平面向量數量積的幾何意義的直接應用，這是一道直接源于課本的試題.在二輪復習過程中多關注研究課本習題、思考題，進行歸類，那么就能很好地幫助同學們整合知識.

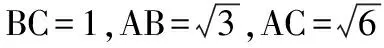
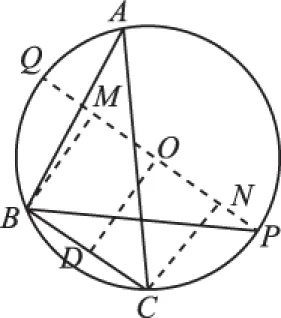
圖2

圖3

【評注】方法二，運用代數運算，解三角形，結合運用特殊化思想，取B,C為特殊點，然后進行數量積的坐標運算，解決問題；而方法一，則按照平面向量數量積的投影意義思路來求解就比較簡捷.由此可知，當數量積中有一個向量的模長為定值(或投影與另一向量的模長關系確定)時可以用平面向量數量積的投影形式解決問題.

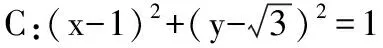
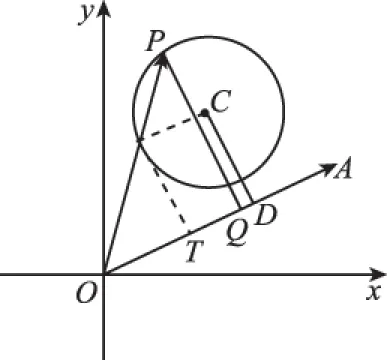
圖4

( )

A.4 B.5 C.7 D.9

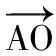
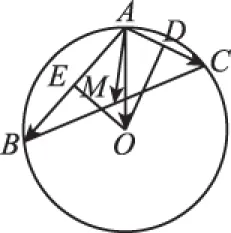
圖5

( )

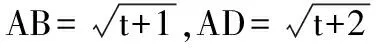
A.1 B.2 C.tD.2t

圖6

二、不識廬山真面目，只緣身在此山中——善用平面向量數量積之余弦定理形式

圖7

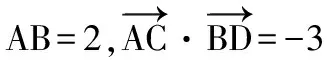
圖8

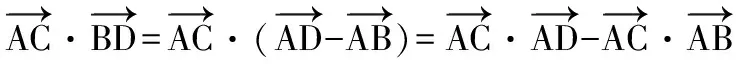
在△ABC中，由平面向量數量積余弦定理形式知：

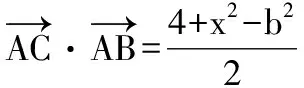
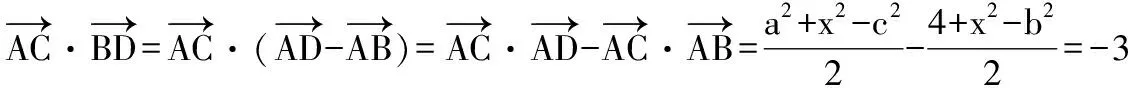
即c2=a2+b2+2.

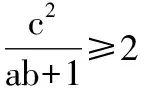
【評注】利用平面向量數量積之余弦定理形式較快地解決了這個問題.正如教科書108習題B組第5題所說,利用好向量數量積可以容易地推導關于三角形、四邊形、圓等平面圖形的一些性質.從此例可以發現常用的一些技巧方法，結論，其實很多的都來源于課本，只要我們能真正地理解課本，挖掘課本中的隱含知識、延伸知識，很多的問題的解決方法都可以在課本上找到.因此高三二輪復習時，不但不要完全的脫離課本，而且要多與課本相聯系，多多關注到課本例習題.

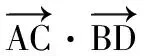
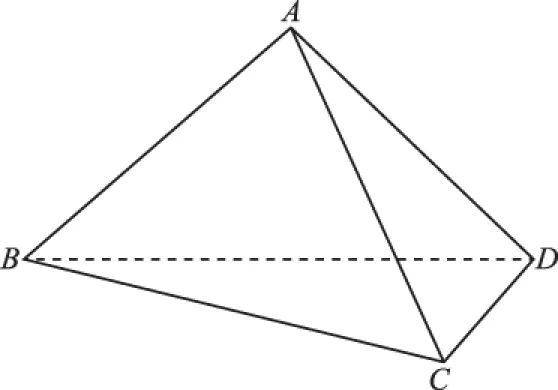
圖9

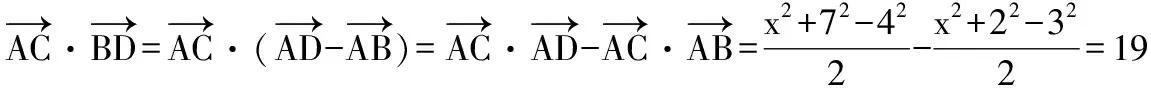
三、輕沙走馬路無塵——巧用平面向量數量積之極化恒等式形式

人教版必修四教材第109頁平面向量應用舉例中有此例：如圖10，你能發現平行四邊形的對角線長度和兩條鄰邊長度之間的關系嗎？

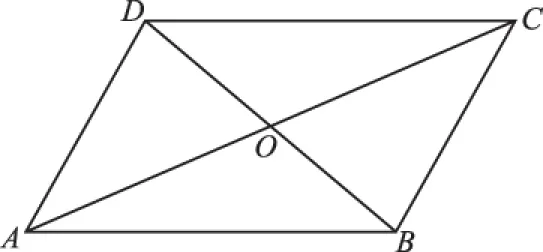
圖10

( )

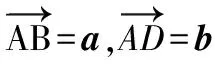
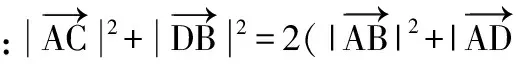
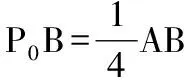
圖11

A.∠ABC=90°

B.∠BAC=90°

C.AB=AC

D.AC=BC

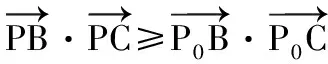
∴Δ=(1+a)2-4a≤0，得a=1，

∴H為AB的中點，∴AC=BC，故選D.

圖12

方法二：(利用平面向量數量積之極化恒等式)

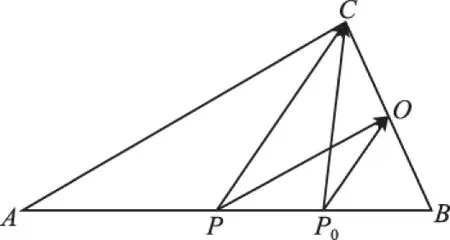
圖13

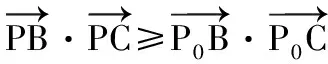
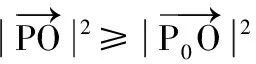
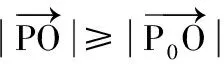
∴OP0⊥BC，即有：當AP⊥BC時，P為BC的中點.

∴AC=BC，故選D.

【評注】此題方法一、二分別利用了平面向量數量積的幾何意義(投影形式)和極化恒等式，轉化為可借助圖中平面幾何知識就可以解決問題，解法顯得快捷簡潔.

( )

A.C0M⊥AB

B.C0M⊥l，其中l是拋物線過C0的切線

C.C0A⊥C0B

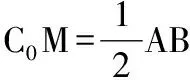
答案：B

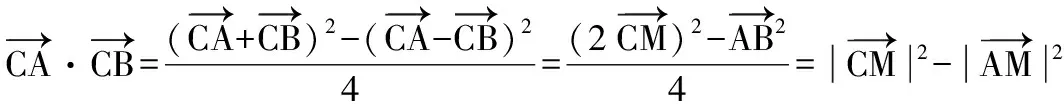
∴C0M⊥l，其中l是拋物線過C0的切線.

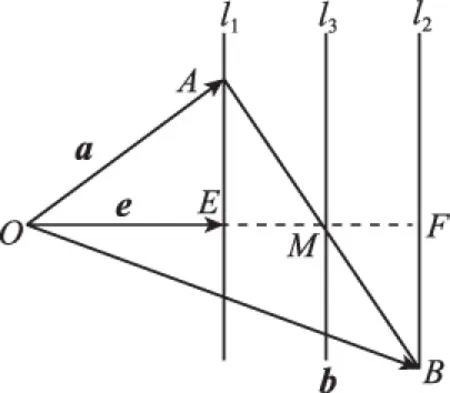
圖14

(作者單位：浙江省開化中學)