基于格的前向安全無證書數字簽名方案

徐 潛 譚成翔 馮 俊 樊志杰 朱文燁

(同濟大學電子與信息工程學院計算機科學與技術系 上海 201804)

?

基于格的前向安全無證書數字簽名方案

徐 潛 譚成翔 馮 俊 樊志杰 朱文燁

(同濟大學電子與信息工程學院計算機科學與技術系 上海 201804)

(1062842783@qq.com)

無證書簽名方案利用密鑰生成中心與用戶共同生成簽名密鑰的方式，解決了傳統的基于身份的數字簽名方案中存在的密鑰托管問題.目前，針對無證書簽名方案的研究還存在3點可以改進的地方:1)已有的基于隨機格構建的無證書簽名方案，雖然具有后量子安全性，但都是建立在隨機預言模型下，尚無針對標準模型的相關研究；2)已有的格基無證書簽名方案大多只考慮外部敵手，缺乏抵御不誠實用戶攻擊的能力；3)已有的無證書簽名方案均需要保證用戶密鑰是絕對安全的，無法解決密鑰泄露問題.針對這3點不足，在隨機預言模型下的前向安全的無證書格基簽名方案的基礎上，首次提出了標準模型下可證明安全的基于隨機格的前向安全無證書數字簽名方案，并在不引入第三方代理的前提下同時解決了密鑰泄露和密鑰托管問題.在面對不誠實的用戶和惡意密鑰生成中心2類強敵手的情況下，利用小整數解SIS假設證明了所提出的方案具有適應性選擇消息、選擇身份攻擊下的前向安全強不可偽造性.

格基數字簽名；無證書；前向安全；隨機預言模型；標準模型

傳統的基于公鑰基礎設施(public key infrastr-ucture, PKI)的公鑰密碼系統通過引入證書管理機構CA為用戶頒發數字證書，并鑒權用戶身份.然而，證書的更新、撤銷等管理操作給系統帶來較大的運行負荷.為了消除證書管理帶來的昂貴開銷，Shamir[1]于1984年提出了身份基加密的思想，利用用戶唯一的公共標識ID作為用戶的公鑰，由密鑰生成器(private key generator, PKG)為用戶生成密鑰.目前已有很多高效的身份基簽名方案[2-5]，如Yao等人[2]利用拉格朗日插值公式，在隨機格的基礎上構建了允許模糊身份驗證的身份基簽名方案.以及Wei等人[3]提出的門限身份基簽名方案等.然而，由于用戶密鑰完全由PKG生成，對PKG可見，一旦PKG受到污染，整個系統中的用戶都將不再安全，這就產生了密鑰托管問題(key escrow).

Al-Riyami等人[6]在2003年首次定義了無證書公鑰密碼學的概念，用來解決密鑰托管問題并消除證書管理的開銷.無證書密碼學的核心思想為：密鑰生成中心(key generation centre, KGC)為用戶派發部分密鑰，用戶自己負責剩余密鑰，即私密值的生成，用戶完整的簽名密鑰由部分密鑰和私密值共同組成.由于KGC無法獲取用戶的私密值，也就無法知曉用戶的完整密鑰，從而消除了惡意KGC帶來的安全隱患，解決了密鑰托管問題.無證書密鑰方案可以用于移動環境下用戶敏感數據的保護或者高效的授權認證等領域.

基于Al-Riyami的思想，很多無證書數字簽名方案被陸續提出[7-15].這些方案的安全性都是基于傳統數論難題，如離散對數和大整數分解等.然而隨著量子計算機的發展，基于傳統數論難題的密碼方案的安全性受到了挑戰.事實上，早在1997年，Shor[16]就提出了多項式時間內解決離散對數和大整數素分解的量子算法.因此，構建能夠抵御量子攻擊的后量子安全的無證書簽名方案就具有十分重要的意義.為此，Kim等人[17]和Tian等人[18]設計了基于格的無證書簽名方案，并通過小整數解(short integer solution, SIS)問題證明了方案的安全性.但是他們的方案以及安全證明都是基于隨機預言模型，在實際應用中，很難保證諸如Hash函數等對象可以按照在隨機預言證明中所假設的那樣，實現完全的隨機化，從而難以保證系統的實際安全性[19].同時，他們的方案只考慮外部敵手，忽視了來自于內部不誠實簽名用戶的威脅.

更進一步地，在移動環境下特別是隨著手機等移動端的大量使用，由于用戶的不安全行為，一旦移動設備被攻擊，存儲在設備中的用戶簽名密鑰將很容易被竊取，即存在密鑰泄露問題.目前后量子安全的無證書簽名方案[17-18]等均假設用戶密鑰是絕對安全的，缺乏有效解決密鑰泄露問題的能力.同時，基于傳統數論難題的無證書簽名方案雖然考慮了密鑰泄露問題，但主要通過引入第三方代理來更新用戶密鑰，不僅增加了系統的復雜度，而且，由于第三方代理的安全性無法保證，系統的安全隱患也隨之增加.

綜上所述，目前無證書簽名方案存在3個問題：

1) 已有基于格的后量子安全的無證書簽名方案僅僅基于隨機預言模型，無法保證實際應用中的系統安全性；

2) 已有無證書簽名方案的安全證明主要考慮外部敵手和惡意密鑰生成中心，而對來自于不誠實的簽名用戶的威脅抵抗能力不足；

3) 目前無證書簽名方案還無法在不引入第三方代理的前提下解決密鑰泄露問題.

針對這3個主要問題，本文利用格基委派技術，基于隨機格理論，首先在隨機預言模型下引入了前向安全的無證書數字簽名方案RO_LFC_SIG，并在此基礎上，設計了第1個標準模型下可證安全的前向安全無證書ST_LFC_SIG方案.

本文的主要貢獻有4個方面：

1) 針對不誠實的用戶和內部惡意KGC攻擊者，首次形式化定義了前向安全強不可偽造性的安全模型.與文獻[8，18，20-21]中的安全模型相比，不僅增加了針對密鑰泄露的前向安全性部分，而且將外部敵手增強為不誠實的簽名用戶，使得方案安全性更高.

2) 首次具體實現了基于格的前向安全無證書簽名方案，將前向安全與無證書方案基于隨機格結合，在不引入第三方代理的條件下同時解決密鑰泄露和密鑰托管問題，且具有后量子安全性.

3) 提出的ST_LFC_SIG無證書簽名方案不僅具有前向安全性，也是首個在標準模型下可證安全的格基無證書簽名方案，與文獻[17-18]中的格基簽名方案相比，安全性更高.

4) 分別在隨機預言模型和標準模型下，利用隨機格的小整數解SIS難題，證明了提出的2個簽名方案在面對2類強敵手時，具有適應性選擇消息、選擇身份攻擊的前向安全強不可偽造性(forward secure and strongly existentially unforgeable against adaptive chosen message and adaptive chosen identity attack, FSU-AMAIA)；通過與已有的格基簽名方案和無證書簽名方案進行安全性和效率的對比，證明本文方案在保證較低的漸近性復雜度的同時，達到了更好的安全性.

1 相關工作

無證書數字簽名方案的研究目前已有很多，例如Yu等人[7]就是利用雙線性對構造了無證書簽名方案；Guan等人[8]通過應用公鑰替換攻擊證明了Yu等人[7]方案并不是存在不可偽造的；Yeh等人[9]通過橢圓曲線設計了無證書簽名方案，但是只考慮了第三方敵手的攻擊；陳虎等人[10]將無證書簽名與群簽名結合，基于雙線性對設計了高效的無證書群簽名方案，實現了群成員的動態更新；Choi等人[12]基于計算性Diffie-Hellman假設(computational Diffie-Hellamn, CDH)構造了高效的無證書簽名方案，但主要實現了存在不可偽造性而非強不可偽造；Huang等人[13]構造了能夠抵御2類強敵手的無證書簽名方案，并基于提出的簽名方案設計了身份鑒權協議；Tso等人[14]基于CDH假設并針對公鑰替換攻擊問題設計了強不可偽造的無證書簽名方案；同樣基于CDH假設的還有Chen等人[15]的方案.以上的無證書簽名方案[7-15]都是基于傳統數論難題的，不具備后量子安全性；Kim等人[17]和Tian等人[18]設計了基于格的隨機預言模型下可證安全的無證書簽名方案，并通過小整數解SIS問題證明了方案的存在不可偽造性；文獻[17-18]的方案實現了后量子安全的無證書簽名方案，但是隨機預言模型無法保證方案的實際安全性，其安全證明也只考慮了外部敵手，沒有針對不誠實用戶的安全性分析.同時，文獻[17-18]的簽名方案依賴于絕對安全的用戶密鑰，因此存在密鑰泄露問題.

解決密鑰泄露問題的一種有效的方法是構建前向安全的公鑰密碼系統.針對密鑰泄露的前向安全性是指，某一個時刻用戶密鑰的泄露不會危及之前任意時刻的方案的安全性.在前向安全的數字簽名研究方面，目前采用的主要思想是構建不可逆的密鑰更新算法.已有很多前向安全的簽名方案[22-25]，例如Yu等人[22]的方案；Ebri等人[23]賦予用戶指定密鑰更新時間的能力；文獻[24]則將前向安全與門限簽名相結合，利用周期性密鑰更新和群組門限同時保證密鑰的安全性；文獻[25]中利用時間序列樹等實現了前向安全的細粒度屬性控制.但同很多無證書密碼方案一樣，這些前向安全的簽名方案仍然是基于雙線性對等數學難題，不具有抗量子計算攻擊的能力；Zhang等人[20]設計了首個基于格的前向安全的簽名方案FSIBS，其主要的思路是建立在Rückert[26]的分層的身份基簽名方案的基礎上，利用格基委派算法實現密鑰的前向更新；然而同文獻[17-18]中的方案一樣，Zhang等人[20]的方案也僅僅實現了隨機預言模型下的證明；而且Zhang等人[20]的方案只考慮了外部敵手，不具備抵抗惡意KGC攻擊的能力，安全模型也僅考慮了存在不可偽造性而缺乏針對前向安全性的形式化定義；Li等人[27]仍然基于雙線性對考慮了前向安全與無證書方案的結合問題，沒有給出安全模型的形式化定義，而且文獻[27]通過引入第三方代理實現前向安全性，增加了方案復雜度，也沒有證明當第三方代理受到攻擊時方案的可靠性.

2 預備知識

標識與記號：設q為正素數，q表示]范圍內的整數.表示向量v的l2范數.本文中使用標準的O記號表示函數的復雜度上界，即g(n)=O(f(n))當且僅當存在正常數c和n0，使得對任意的n≥n0有成立.相應地，定義下界復雜度記號ω，即g(n)=ω(f(n))當且僅當存在正常數c和n0，使得對任意的n≥n0有成立.定義關于n的可忽略函數negl(n)，使得對任意多項式g(n)，當n足夠大時都有.如果概率p=1-negl(n)則稱概率是壓倒性成立的，若p=negl(n)，則稱概率是可忽略的.

定義1. 小整數解問題SIS[28]：給定一個正整數q，隨機矩陣A∈q，實數β，定義(q,m,β)上的SIS問題PSIS(q,m,β)是：找到非0向量v∈m，使得Av=0 modq并且≤β.Micciancio等人[29]已經證明，對任意多項式有界的，平均情況下的PSIS(q,m,β)問題與解決最壞情況下格上的近似獨立向量問題是同等困難的.

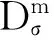
引理2[28]. 無抽樣技術：若簽名人從某個隨機分布中抽取y，簽名的目標分布為f(x)，與簽名人私鑰sk無關，實際分布為g(x)，可能與sk有關，且對于任意x及某個正實數M有f(x)≤Mg(x).則以概率f(y)Mg(y)輸出簽名y將使得y服從分布f(x).

由引理1，若設M=e，以(y)輸出簽名y，則y服從于分布且以壓倒性的概率滿足.

引理3. 陷門生成算法[30]：設q≥3，m≥5nlbq，存在有效的多項式時間算法TrapGen在多項式時間內生成統計接近于n×mq上隨機分布的矩陣A以及整數格Λ⊥(A)的短基TA∈m×m，設Gram-Schmidt正交化后為A，則以壓倒性概率成立.

引理4. 原像抽樣算法[31]：設q≥3，m≥O(nlbq)，隨機矩陣A∈n×mq以及整數格Λ⊥(A)的短基TA∈m×m，設高斯參數，那么對任意的u∈，存在有效的多項式時間算法SamplePre(A,TA,s,u)，統計近似于從離散高斯分布GΛu(A),s中抽取向量v∈Λu(A).由高斯分布的性質，v將以壓倒性的概率滿足.其中Λu(A)={e∈m:Ae=umodq}.可以很容易的擴展到矩陣的原像抽樣算法，即：

對任意的矩陣U∈n×k，其余參數與基本的原像抽樣算法相同，存在擴展的多項式時間算法SamplePre(A,TA,s,U)，統計近似于從離散高斯分布GΛU(A),s中得到矩陣V∈Λu(A)，且AV=Umodq.同時以壓倒性概率成立.

引理5. 格基委派算法[32]：設q上小范數可逆矩陣(按離散高斯分布獨立抽取每一列)的集合為Dm×m，矩陣A∈n×mq，整數格Λ⊥(A)的短基TA∈m×m，高斯參數，矩陣R←Dm×m，存在多項式時間算法BasicDel(A,R,TA,s)輸出格Λ⊥(B=AR-1)的短基).且不存在多項式時間BasicDel的求逆運算.存在多項式時間算法SampleRwithBasis(A)輸出矩陣R←Dm×m以及格Λ⊥(B=AR-1)的短基).存在確定性的多項式算法ExtBasis(F=A|C,TA)輸出A|C對應的整數格Λ⊥(A|C)的基TF，且.

定義2. 本文提出的數字簽名方案包括5個多項式時間算法：

1) 系統建立Setup.由密鑰生成中心KGC運行，輸入安全參數n，輸出系統公共參數PP和主密鑰MSK.

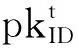
3) 密鑰更新算法Update.輸入用戶當前ID與更新的時間區間，KGC與用戶交互完成密鑰更新.

4) 簽名算法Sign.輸入系統公共參數、用戶公鑰與私鑰、待簽名消息、輸出簽名.

5) 驗證算法Verify.輸入系統公共參數、簽名消息、用戶公鑰與用戶ID以及簽名，算法判斷該簽名是否是有效簽名.

定義3. 前向安全強不可偽造性FSU-AMAIA：定義2類多項式時間強敵手：1)強敵手A1模擬內部不誠實的用戶，不誠實的用戶指在簽名過程中，會在未獲得合法部分密鑰的情況下嘗試偽造自己或其他用戶的簽名，顯然，偽造自身某一時刻的簽名需要的安全性更高；2)強敵手A2模擬惡意的密鑰生成中心KGC，在文獻[8，18]中提出的安全模型的基礎上，給出針對2類強敵手的安全游戲Game1與Game2，如果敵手A1與A2分別贏得Game1和Game2的概率是可忽略的，則稱簽名方案在適應性選擇消息、選擇身份攻擊下對強敵手是前向安全強不可偽造的，游戲Gameb,b∈{1,2}具體描述如下.

1) 系統建立Setup.輸入安全參數n，挑戰者C生成系統公共參數PP與主密鑰MSK，如果b=1，C將PP發送給敵手A1，否則，將PP和MSK一起發給A2.

2) 敵手適應性的進行如下問詢.

① 公鑰問詢：敵手提交{ID,t}，挑戰者返回相應的公鑰回答問詢.

② 密鑰問詢：敵手Ab提交{ID,t}，如果b=1，挑戰者C生成用戶的部分簽名密鑰并發送給敵手.同時，敵手可以問詢除自己之外的其他用戶的私密值.注意如果{ID,t}對應的公鑰發生過替換，挑戰者返回⊥.如果b=2，密鑰問詢只包括私密值問詢，挑戰者返回私密值給敵手.

③ 公鑰替換問詢：敵手可以替換任意身份下的公鑰.

④ 密鑰更新問詢：敵手Ab提交更新時間區間與身份，挑戰者返回更新后的密鑰作為應答.

⑤ 簽名問詢：敵手Ab問詢關于任意消息的簽名，挑戰者生成消息的簽名并返回給敵手.注意如果相應的公鑰被敵手替換過，則敵手需要提交對應的私密值.

敵手Ab可以選擇變更用戶身份或簽名時刻并問詢密鑰和簽名，也可以直接進入偽造階段.

3) 偽造Forgery.敵手Ab輸出以身份ID*，時刻t*下的關于消息μ*的簽名e*，敵手Ab贏得游戲當且僅當：

①Verify(ID*,e*,μ*,t*)=Accept；

② 若b=1，(ID*,t*)未作為密鑰問詢的輸入；若b=2，(ID*,t≤t*)未作為私密值問詢的輸入；

③ 若b=1，(ID*,ti,t*)未作為密鑰更新問詢的輸入；若b=2，(ID*,ti,tj≤t*)未作為密鑰更新問詢的輸入；

④ 若b=2，(ID*,t≤t*)未作為公鑰替換問詢的輸入；

⑤e*未作為簽名問詢的應答返回給敵手.

若敵手Ab獲勝的概率為AdvAb=Pr[Forgery(ID*,e*,μ*,t*)=Success]，則當且僅當AdvAb關于安全參數n是可忽略的時，簽名方案是適應性選擇消息、選擇身份攻擊下前向安全強不可偽造FSU-AMAIA安全的.

3 隨機預言模型下的簽名方案RO_LFC_SIG

本節給出隨機預言模型下的前向安全的格基無證書數字簽名方案RO_LFC_SIG，作為構建標準模型下前向安全無證書簽名方案的基礎.RO_LFC_SIG方案具體包括5個多項式時間的算法.

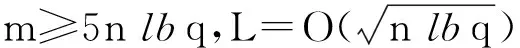
KGC運行〈A,TA〉=TrapGen(n,q,m)，得到近似隨機矩陣A∈n×mq及整數格Λ⊥(A)的基).設高斯參數，參數序列{σ0,σ1,…,σT}，其中σ0=ω(lbm)，σi≥m3i2ω(lbm)2i+1.設離散正態分布參數.隨機矩陣B∈n×mq.

KGC公布公共參數PP={A,B,H1,H2,H3}，主密鑰MSK={TA}.

2) 密鑰提取KeyExtract.給定PP、ID、密鑰生

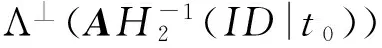
3) 密鑰更新KeyUpdate.假設密鑰更新時間區

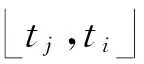
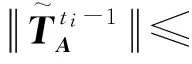
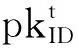
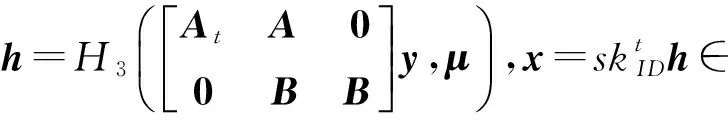
5) 驗證算法Verify.輸入(ID,(ε,h),μ,t)，算法輸出Accept當且僅當：

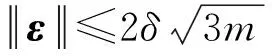
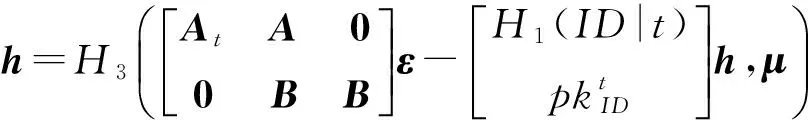
正確性：

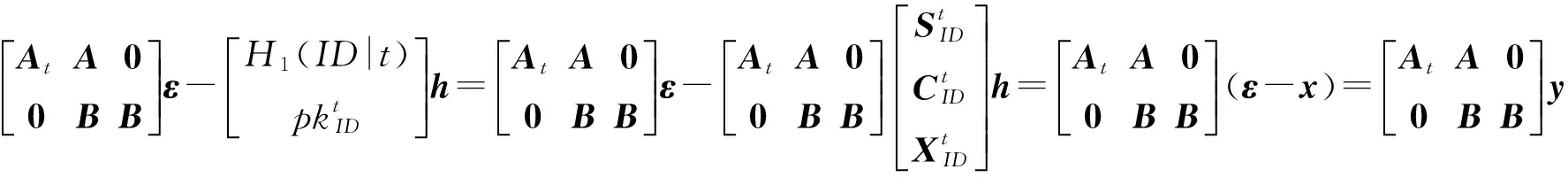
4 RO_LFC_SIG的安全性分析

本節基于SIS假設證明隨機預言模型下方案的前向安全強不可偽造性.不失一般性，設敵手的問詢時刻為[1,T]區間上的連續值，時刻t0=1.設Q為總的問詢身份數，TSam,TBas,TTrap,TSamRwithBas,TExt為算法,BasicDel,TrapGen,SampleRwithBasis以及ExtBasis運行時間，Tmul為一次m×m矩陣乘法的近似運行時間.

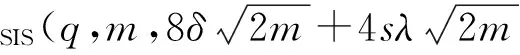
證明. 假設存在敵手A1可以偽造簽名，則可以如下構造多項式算法.

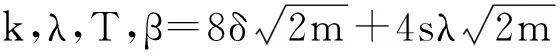
挑戰者C隨機選擇A0∈n×mq為SIS實例，隨機矩陣B∈n×mq，維護4個Hash列表LH1,LH2,LH3,Lsig.C從G逐列采樣選取t*個可逆的小范數矩陣Ri∈m×mq，并設A=A0Rt*Rt*-1…R1，γ∈[1,Q].

C將公共參數PP={A,A0,B,H3}發送給敵手A1.

2) 敵手可以適應性的進行如下問詢.

①H2問詢：敵手提交{ID,ti}，C查找列表LH2判斷是否有對應的Hash值，若有，則直接作為敵手的應答返回敵手，否則，設Dm×m為q上的小范數可逆陣集合.若ID不為第γ次問詢身份，C調用多項式時間函數〈R,TtiAR〉=SampleRwithBasis(A)生成R←Dm×m以及Λ⊥(AR-1)的基TtiAR∈m×m，C設置H2(ID|ti)=R并將其返回給敵手作為應答.同時，將{TtiAR,R}插入到列表LH2中.

若ID為第γ次問詢身份，ti≤t*，C直接令H2(ID|ti)=Rti，TtiAR=⊥，將H2(ID|ti)=Rti返回給敵手，并將{TtiAR,Rti}插入到LH2中.

若ID為第γ次問詢身份，ti=t*+1，C調用SampleRwithBasis(A0)生成R←Dm×m，TtiAR∈m×m.C設置H2(ID|t*+1)=R并將其返回給敵手作為應答.同時，將{TtiAR,R}插入到列表LH2中.

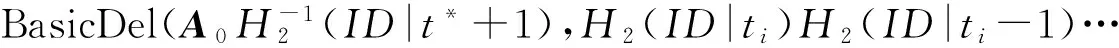
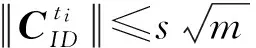
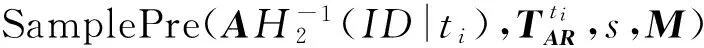
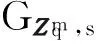
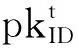
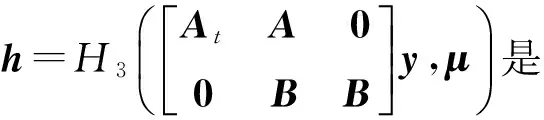
⑨ 簽名問詢：敵手A1提交{ID,t,μ}，C查找LH3,Lsig得到對應的密鑰與h，之后正常簽名并應答敵手.如果{ID,t}對應的公鑰發生過替換，則A1需要提交對應的私密值.

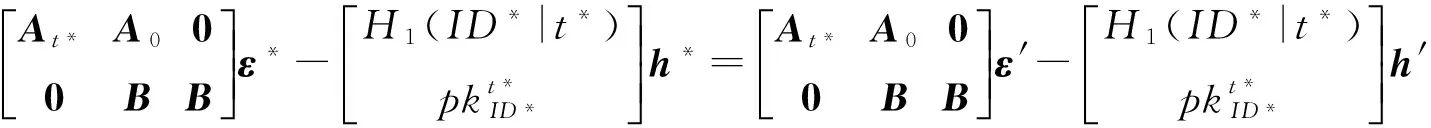
證畢.

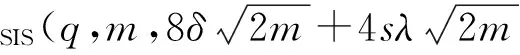
證明. 假設存在敵手A2可以偽造簽名，則構造多項式算法步驟如下.

1) 系統建立Setup.設n,k,λ,T,M,α,m,L,s,t*,γ,β,q,δ以及參數序列{σ0,σ1,…,σT}與定理1中一樣.3個抗碰撞的Hash函數H1,H2,H與RO_LFC_SIG方案中一樣.〈A,TA〉=TrapGen(n,q,m).隨機矩陣B∈n×mq為SIS實例，維護2個Hash列表LH3,Lsig，Lsig中的表項為}.

挑戰者C將公共參數PP={A,B,H1,H2,H3}與主密鑰MSK={TA}發送給敵手A2.

2) 敵手可以適應性的進行如下問詢.

敵手A2已知主密鑰MSK，因此不需要進行部分密鑰問詢.部分密鑰的更新也可以由敵手自己完成.

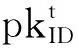
④H3問詢：與定理1相同.

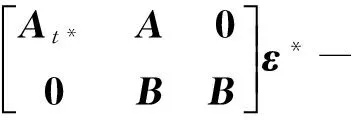
證畢.

5 標準模型下的簽名方案ST_LFC_SIG

隨機預言模型下RO_LFC_SIG簽名方案的安全性依賴于方案所采用的Hash函數的完全隨機性，這在實際應用中可能無法滿足.因此，為了增強格基前向安全的無證書簽名方案的應用性與安全性，我們在RO_LFC_SIG的基礎上，研究了基于標準模型的ST_LFC_SIG方案.本節給出方案的具體實現.

需要注意的是，本文提出的ST_LFC_SIG方案是第1個標準模型下基于格的無證書數字簽名方案，方案具體由5個多項式時間的算法構成.

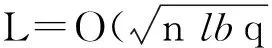
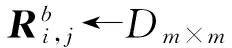
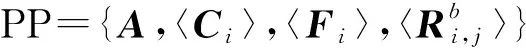
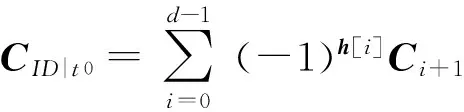
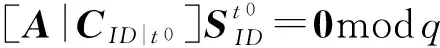
若用戶ID為第1次生成密鑰，運行〈B,TB〉=TrapGen(n,q,m)得到密鑰根矩陣〈B,TB〉.

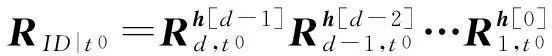
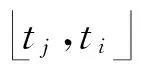
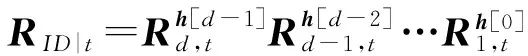
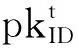
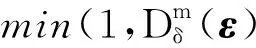
5) 驗證算法Verify.輸入(ID,(ε,h),μ,t)，算法輸出Accept當且僅當：

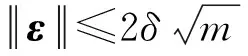
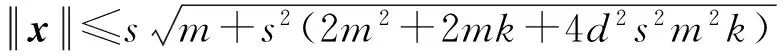
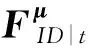
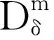
6 ST_LFC_SIG的安全性分析

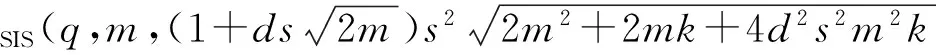
證明. 假設存在敵手A1可以偽造簽名，則構造多項式算法步驟如下.

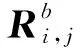
對i∈[1,d]，從分布G中逐列采樣得到小范數矩陣Di∈m×kq，且以壓倒性概率成立.設正整數pi，〈E,TE〉=TrapGen(n,q,k)，Ci=ADi+piE，其中隨機矩陣A∈n×mq為SIS實例.則Ci統計不可區分于n×kq上的隨機均勻矩陣.對i∈[1,l]，設Fi∈n×mq為隨機均勻矩陣.

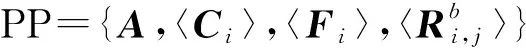
2) 敵手可以適應性地進行如下問詢.

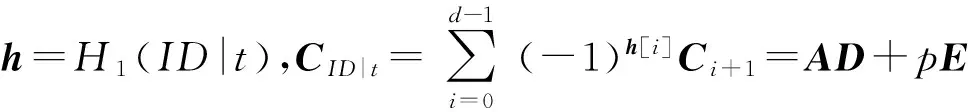
如果p=0 modq第1次出現，C隨機生成(m+k)×m上的矩陣并返回給敵手作為部分密鑰應答，設置Lsig中{ID,t}對應表項的b=1.若p=0不為第1次出現，C終止游戲.

若p≠0，挑戰者C從G中逐列采樣得到矩陣∈m×m.由于TE為Λ⊥(pE)的短基，C可由得到，從而m×m.將作為部分密鑰應答返回敵手.顯然，將保存于Lsig中.

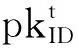
③ 密鑰更新問詢：敵手提交[tj,ti]和ID，挑戰者C調用部分密鑰問詢并以{ID,ti}作為輸入進行部分密鑰更新.如果游戲沒有終止，且ID對應于敵手之外的用戶，則挑戰者C調用KeyUpdate算法完成公鑰和私密值更新.

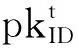
若{ID,t}表項存在，但b=1，C終止游戲.

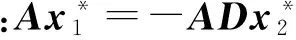
證畢.

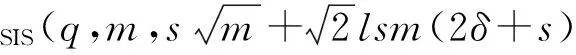
證明. 假設存在敵手A2可以偽造簽名，則構造多項式算法步驟如下.

1) 系統建立Setup.設設n,M,α,k,b,d,l,T,q,m,L,δ,H1,H2，參數序列{σ0,σ1,…,σT}，參數s,δ與定理3中一樣.〈A,TA〉=TrapGen(n,q,m).設i∈[1,d]，隨機均勻小范數矩陣Ci∈n×kq.對i∈[1,l]，逐列從G中采樣得到Di∈m×mq，則Fi=B0Di統計不可區分于n×mq上的隨機均勻分布，其中隨機矩陣B0為SIS實例.

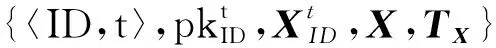
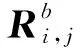
① Setγ∈[1,Q],t*∈[1,T]*ID*為第r次秘鑰問詢對應的身份*

② Foreacht≤t*do

③h=H1(ID*|t)；

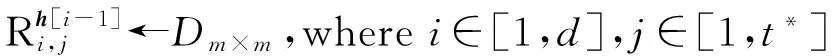
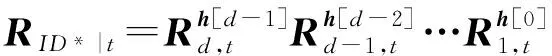
⑥ End Foreach

⑦B=B0RID*|t*RID*|t*-1…RID*|1；*B為ID*對應的秘鑰根矩陣*

⑧B′=B0；

⑨ Forj=t*+1 toT

⑩h=H1(ID*|j-1)；

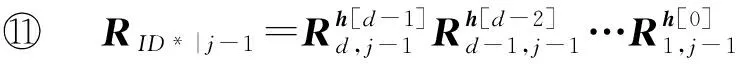
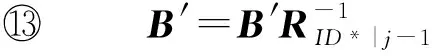
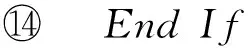
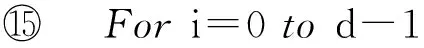
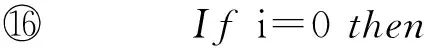
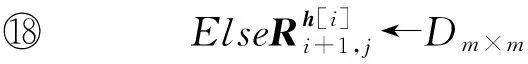
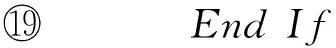
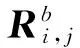
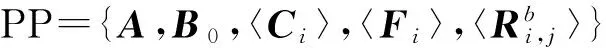
2) 敵手可以適應性地進行如下問詢.

① 公鑰問詢：敵手提交{ID,t}，若ID不為第γ次問詢身份，挑戰者C首先查詢表Lsig看是否有對應于身份ID的密鑰根矩陣.如果沒有，由SampleRwithBasis(B)得到R←Dm×m和Λ⊥(BR-1)的基TBR，C將BR-1作為當前身份ID的密鑰根矩陣，并將其和TBR一起保存到Lsig中.C調用簽名方案的KeyExtract和KeyUpdate(t>1)算法正常計算用戶的公鑰應答.

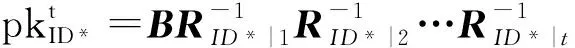
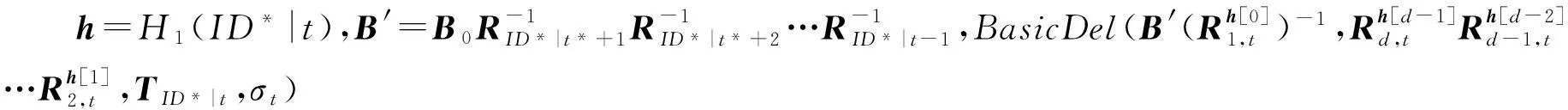
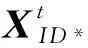
敵手A2已知主密鑰MSK，因此不需要進行部分密鑰問詢.部分密鑰的更新也可以由敵手自己完成.

③ 私密值更新問詢：若ID不為第γ次問詢身份時，敵手公鑰和私密值均正常生成，因此挑戰者C可以直接調用KeyUpdate算法完成更新.

若ID為第γ次問詢身份，設更新區間[tj,ti]，若tj≥t*或ti>t*≥tj，C可以查表Lsig得到時刻t′=max(tj,t*+1)的公鑰和私密值，之后可以調用KeyUpdate算法在[t′,ti]上完成更新.若t*≥ti，C退出.

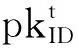
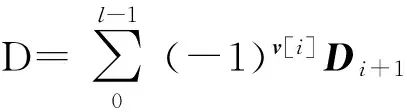
證畢.

7 方案安全性與效率對比分析

文獻[33]對無證書簽名方案的安全模型進行了分析，并依據簽名問詢與私密值問詢，對第1類強敵手和第2類強敵手分別給出了8種和4種不同能力的敵手攻擊等級，歸納如表1和表2所示.N-Sign表示在簽名問詢，若身份ID對應的公鑰發生過替換，則拒絕應答.S-Sign表示無論公鑰是否發生替換，都響應敵手的簽名問詢.

Table 1 Eight Different Attack Levels of Type 1 Adversary表1 敵手1對應的8種攻擊等級

Table 2 Four Different Attack Levels of Type 2 Adversary表2 敵手2對應的4種攻擊等級

由表1和表2可以看出，S -Type 1和S -Type 2類型的S-Type敵手具有最強的攻擊能力.表3將本文提出的隨機預言模型下的RO_LFC_SIG方案與標準模型下的ST_LFC_SIG方案，以及Kim等人[17]和Tian等人[18]的格基無證書簽名方案，和文獻[12-15]中的無證書簽名方案進行安全性對比.

由表3可以看出，本文提出的無證書簽名方案不僅具有抗量子攻擊的能力，具有前向安全性，同時所基于的敵手模型攻擊等級較高，因此方案具有較好的安全性.更進一步地，本文提出的ST_LFC_SIG方案是第1個基于格的標準模型下的無證書簽名方案，較之文獻[12-15，17-18]中以及RO_LFC_SIG隨機預言模型下的簽名方案，在實際應用中的安全性更高.

Table 3 Comparison of Security表3 方案安全性對比

在效率對比方面，本文除了選擇文獻[17-18]中的隨機預言模型下的格基無證書簽名方案外，還選擇了Yao等人[2]和Zhang等人[20]的FSIBS以及Rückert[26]的隨機格簽名方案，雖然后3種方案并不是無證書簽名方案，但由于其均基于隨機格，因此可以作為時間和空間復雜度對比的參照.

設參數與第3節方案中定義的相同，n為安全參數，m≥5nlbq，k為正整數.TSam,TBas,TTrap,TRand,TExt分別為算法SamplePre,BasicDel,TrapGen,RandBasis,ExtBasis運行時間.Tmul為一次標量乘法耗費時間.7種方案的漸近性復雜度對比如表4所示.

Table 4 Comparison of Asymptotic Complexity表4 漸近復雜度對比

設k≤n4，則由表4可以看出，在保證安全性的基礎上，本文方案的公鑰尺寸優于其他的格基或身份基簽名方案.標準模型下的ST_LFC_SIG簽名方案的簽名長度優于除文獻[20]以外的其他方案.在私鑰長度方面，本文方案優于文獻[17，26]的方案，比Yao等人[2]、Tian等人[18]和Zhang等人[20]的FSIBS方案略大.這主要是由于無證書簽名方案需要利用部分密鑰和私密值2個子部分來構造基于隨機格的2個PSIS等式，從而實現對不誠實用戶和惡意KGC的前向安全強不可偽造性，而Zhang等人[20]的方案只考慮了隨機預言模型下的外部敵手.此外，本文通過引入變量k降低了簽名長度，并通過密鑰根矩陣保證了較小的公鑰長度以及安全證明中正確的敵手視角，而文獻[20]中的安全證明由于缺少與身份綁定的密鑰根矩陣的定義，將導致敵手關于同一挑戰身份與挑戰時刻的2次公鑰問詢產生不同的應答結果.而Yao等人[2]和Tian等人[18]的方案則不具備前向安全性.因此與文獻[2,18,20]相比，本文方案的安全性更高.

時間復雜度方面，根據文獻[30-31]，有TExt

由以上分析可知，本文提出的RO_LFC_SIG和ST_LFC_SIG無證書簽名方案首次在不引入第三方代理的條件下基于隨機格實現了前向安全性與無證書的結合.同時，ST_LFC_SIG方案也是第1個基于格的標準模型下可證安全的無證書簽名方案，并解決了密鑰泄露問題.通過以上安全性與效率的對比分析可知，在保證相對較低的時空復雜度的基礎上，隨機預言模型下RO_LFC_SIG方案和標準模型下的ST_LFC_SIG方案均可以達到較好的安全性與實用性.

8 結束語

本文基于格基委派技術，針對密鑰泄露的前向安全性，在提出隨機預言模型下RO_LFC_SIG方案的基礎上，設計了標準模型下前向安全的無證書簽名方案ST_LFC_SIG，并給出了2個方案的具體構造.同時，基于隨機預言模型和標準模型，證明了所提出的方案面對2類強敵手在適應性選擇消息、選擇身份攻擊下的前向安全強不可偽造性FSU-AMAIA.本文方案的安全性建立在不誠實用戶和惡意密鑰生成中心的基礎上，較之已有方案中的外部敵手模型，安全性更高.最后，通過對比分析，證明了本文提出的前向安全無證書簽名方案具有較好的安全性與實用性.

本文提出的ST_LFC_SIG簽名方案是第1個基于隨機格的標準模型下可證安全的無證書數字簽名方案，并結合了前向安全性以抵御密鑰泄露的威脅.

由于本文提出的2個無證書簽名方案主要是基于隨機格進行方案構造，因此依然存在改進的空間，一個潛在的思路是采用理想格替代隨機格優化存儲空間，但是標準模型下基于理想格的簽名方案的安全性證明是目前一個研究難點.因此我們下一步的研究目標將集中在設計基于理想格的前向安全無證書簽名方案，以提高方案的整體效率.

[1]Shamir A. Identity-based cryptosystems and signature schemes[G]LNCS 196: Proc of the CRYPTO 1984. Berlin: Springer, 1985: 47-53

[2]Yao Yanqing, Li Zhoujun. A novel fuzzy identity based signature scheme based on the short integer solution problem[J]. Computers and Electrical Engineering, 2014, 40(6): 1930-1939

[3]Wei Baodian, Du Yusong, Zhang Huang, et al. Identity-based threshold ring signature from lattices[G]LNCS 8792: Proc of the 8th Int Conf on Network and System Security. Berlin: Springer, 2014: 233-245

[4]Tian Miaomiao. Identity-based proxy re-signatures from lattices[J]. Information Processing Letters, 2015, 115(4): 462-467

[5]Kim K S, Hong D W, Jeong I R. Identity-based proxy signature from lattices[J]. Journal of Communications and Networks, 2013, 15(1): 1-7

[6]Al-Riyami S, Paterson K G. Certificateless public key cryptography[G]LNCS 2894: Proc of the ASIACRYPT 2003. Berlin: Springer, 2003: 452-473

[7]Yu Yong, Mu Yi, Wang Guilin, et al. Improved certificateless signature scheme provably secure in the standard model[J]. Information Security IET, 2012, 6(2): 102-110

[8]Guan Chaowen, Weng Jian, Deng R H, et al. Unforgeability of an improved certificateless signature scheme in the standard model[J]. Information Security IET, 2014, 8(5): 273-276

[9]Yeh K H, Tsai K Y, Fan C Y. An efficient certificateless signature scheme without bilinear pairings[J]. Multimedia Tools and Applications, 2015, 74(16): 6519-6530

[10]Chen Hu, Zhu Changjie, Song Rushun. Efficient certificateless signature and group signature schemes[J]. Journal of Computer Research and Development, 2010, 47(2): 231-237 (in Chinese)(陳虎, 朱昌杰, 宋如順. 高效的無證書簽名和群簽名方案[J]. 計算機研究與發展, 2010, 47(2): 231-237)

[11]Du Hongzhen, Wen Qiaoyan. Security analysis of two certificateless short signature schemes[J]. Information Security IET, 2014, 8(4): 230-233

[12]Choi K, Park J H, Lee D H. A new provably secure certificateless short signature scheme[J]. Computers & Mathematics with Applications, 2011, 61(7): 1760-1768

[13]Huang X, Mu Y, Susilo W, et al. Certificateless signatures: New schemes and security models[J]. Computer Journal, 2012, 55(4): 457-474

[14]Tso R, Huang X, Susilo W. Strongly secure certificateless short signatures[J]. Journal of System & Software, 2012, 85(6): 1409-1417

[15]Chen Yuchi, Tso R, Horng G, et al. Strongly secure certificateless signature: Cryptanalysis and improvement of two schemes[J]. Journal of Information Science and Engineering, 2015, 31(1): 283-296

[16]Shor P W. Polynomial-time algorithm for prime factorization and discrete logarithm on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5): 1484-1509

[17]Kim K S, Jeong I R. A new certificateless signature scheme under enhanced security models[J]. Security and Communication Networks, 2015, 8(5): 801-810

[18]Tian Miaomiao, Huang Liusheng. Certificateless and certificate-based signatures from lattices[J]. Security and Communication Networks, 2015, 8(8): 1575-1586

[19]Bellare M, Boldyreva A, Palacio A. An uninstantiable random oracle-model scheme for a hybrid-encryption problem[G]LNCS 3027: Proc of the EUROCRYPT 2004. Berlin: Springer, 2004: 171-188

[20]Zhang Xiaojun, Xu Chunxiang, Jin Chunhua, et al. Efficient forward secure identity-based shorter signature from lattice[J]. Computers and Electrical Engineering, 2013, 40(6): 1963-1971

[21]Bellare M, Neven G. Multi-signatures in the plain public-key model and a general forking lemma[C]Proc of the 13th ACM Conf on Computer and Communications Security. New York: ACM, 2006: 390-399

[22]Yu Jia, Hao Rong, Kong Fanyu, et al. Forward-secure identity-based signature: Security notions and contribution[J]. Information Sciences, 2011, 181(3): 648-660

[23]Ebri N, Baek J, Shou F A. Forward-secure identity-based signature: New generic constructions and their applications[J]. Journal of Wireless Mobile Network, 2013, 4(1): 32-54

[24]Yu Jia, Kong Fanyu, Hao Rong, et al. A note on a forward secure threshold signature scheme from bilinear pairings[J]. Journal of Computer Research and Development, 2010, 47(4): 605-612 (in Chinese)(于佳, 孔凡玉, 郝蓉, 等. 一個基于雙線性映射的前向安全門限簽名方案的標注[J]. 計算機研究與發展, 2010, 47(4): 605-612)

[25]Wei Jianghong, Liu Wenfen, Hu Xuexian. Forward-secure ciphertext-policy attribute-based encryption scheme[J]. Journal on Communications, 2014, 35(7): 38-45 (in Chinese)(魏江宏, 劉文芬, 胡學先. 前向安全的密文策略基于屬性加密方案[J]. 通信學報, 2014, 35(7): 38-45)

[26]Rückert M. Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles[G]LNCS 6061: Post-Quantum Cryptography. Berlin: Springer, 2010: 182-200

[27]Li Jiguo, Li Yanqiong, Zhang Yichen. Forward secure certificateless proxy signature scheme[G]LNCS 7873: Proc of the 7th Int Conf on Network and System Security. Berlin: Springer, 2013: 350-364

[28]Lyubashevsky V. Lattice signatures without trapdoors[G]LNCS 7237: Proc of the EUROCRYPT 2012. Berlin: Springer, 2012: 738-755

[29]Micciancio D, Regev O. Worst-case to average-case reductions based on Gaussian measures[J]. SIAM Journal on Computing, 2007, 37(1): 267-302

[30]Alwen J, Peikert C, et al. Generating shorter bases for hard random lattices[J]. Theory of Computer Systems, 2011, 48(3): 535-553

[31]Gentry C, Peikert C, Vaikuntanathan V. Trapdoors for hard lattices and new cryptographic constructions[C]Proc of the 14th Annual ACM Int Symp on Theory of Computing. New York: ACM, 2008: 197-206

[32]Agrawal S, Boneh D, Boyen X. Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE[G]LNCS 6223: Advances in Cryptology (CRYPTO 2010). Berlin: Springer, 2010: 98-115

[33]Yu Chichen, Tso R. A survey on security of certificateless signature schemes[J]. IETE Technical Review, 2016, 33(2): 115-121

Xu Qian, born in 1986. PhD candidate. His main research interests include cryptography, cloud computing security and industrial control safety.

Tan Chengxiang, born in 1965. Professor and PhD supervisor. His main research interests include information security, cloud computing security and applied cryptography (Jerrytan@tongji.edu.cn).

Feng Jun, born in 1985. PhD candidate. His main research interests include security measure, security audit and mobile security (109056396@qq.com).

Fan Zhijie, born in 1982. PhD candidate. His main research interests include cyber security, cloud computing security and mobile security (1310898@tongji.edu.cn).

Zhu Wenye, born in 1991. PhD candidate. His main research interests include information security, security measure and mobile security (1549160994@qq.com).

Lattice-Based Forward Secure and Certificateless Signature Scheme

Xu Qian, Tan Chengxiang, Feng Jun, Fan Zhijie, and Zhu Wenye

(DepartmentofComputerScienceandTechnology,CollegeofElectronicsandInformationEngineering,TongjiUniversity,Shanghai201804)

Certificateless signature scheme has solved key escrow problems existing in traditional identity-based signature schemes. The secret key of the user in certificateless signature scheme consists of two parts, one is partial secret key, which is generated by key generation centre, and the other is secret value from user itself. However, there are still three points to be improved in such scheme. Firstly, although some lattice-based certificateless signature schemes based on the random oracle model have been proposed in order to achieve the post-quantum security, their standard model counterparts remain unrealized. Secondly, most of the existing lattice-based certificateless signature schemes only consider the outside attacker and neglect the threats from semi-trusted user. Thirdly, the existing certificateless signature schemes all rely on the security of the secret key, which cannot be satisfied due to the key exposure problem. In this paper, based on the forward secure and certificateless signature scheme in the random oracle model, we propose the first lattice-based certificateless signature scheme which is provably secure in the standard model to eliminate key exposure and key escrow problems without introducing a third party proxy. With the help of the small integer solution problem, we have proved that our schemes can guarantee the forward secure and strongly existential unforgeability against the adaptive chosen message and adaptive chosen identity attack.

lattice-based signature scheme; certificateless; forward secure; random oracle model; standard model

2016-06-13；

2016-08-23

國家重點研發計劃項目(2017YFB0802302) This work was supported by the National Key Research and Development Program of China (2017YFB0802302)

譚成翔(jerrytan@tongji.edu.cn)

TP309