雙層藥型罩形成的串聯爆炸成型彈丸速度計算模型

王哲， 蔣建偉， 王樹有， 任芮池

(北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

雙層藥型罩形成的串聯爆炸成型彈丸速度計算模型

王哲， 蔣建偉， 王樹有， 任芮池

(北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

針對典型雙層藥型罩爆炸成型彈丸(EFP)裝藥結構，基于微元爆轟驅動及碰撞理論，考慮藥型罩軸向驅動及徑向壓垮特性，建立了雙層藥型罩串聯EFP速度分析模型。計算結果表明：罩微元徑向壓垮引起的內外罩EFP軸向速度差是串聯EFP分離的核心因素；外罩EFP速度隨外罩曲率及外罩所占厚度比增加而增加；內罩EFP速度隨外罩曲率增加而減小，隨外罩所占厚度比增加而增加。結合數值模擬與脈沖X光成型試驗對所推導理論進行了驗證，三者所得到的串聯EFP速度吻合較好。

兵器科學與技術； 爆轟； 串聯爆炸成型彈丸； 雙層藥型罩； 速度

0 引言

隨著各種目標的防護能力不斷加強，新型裝甲的出現使傳統反裝甲聚能戰斗部受到嚴峻挑戰。研究人員嘗試應用新的技術途徑和措施應對這種挑戰，從而涌現出了若干新型反裝甲彈藥。串聯爆炸成型彈丸(EFP)就是其中之一。同軸放置的兩層藥型罩，通過合理設計其形狀和材料組合，在炸藥爆轟驅動下能形成兩個同軸度很高的分離EFP或是單一大長徑比EFP，可應付復合裝甲、爆炸反應式裝甲等新型防護結構的挑戰，提高對裝甲目標的侵徹能力。國內外已有不少學者開展了相關理論、數值模擬及試驗研究[1-8]，鄭宇[9]基于瞬時爆轟理論，雖建立了串聯EFP速度分析模型，但該模型忽略徑向稀疏波作用，簡化內外罩微元碰撞作用，且EFP與射流藥型罩微元壓垮過程不盡相同，尚不能很好地描述帶殼裝藥雙層藥型罩形成的串聯EFP速度。

針對典型雙層藥型罩裝藥結構，考慮徑向稀疏波對裝藥軸向驅動藥型罩微元的影響，基于藥型罩微元徑向壓垮及碰撞理論建立了雙層藥型罩形成的串聯EFP速度計算模型，并分析裝藥結構參數對雙層EFP速度影響。同時采用數值模擬及對計算模型進行驗證，計算結果與數值模擬結果吻合較好。本文的研究結果對雙層藥型罩EFP設計具有一定參考意義。

1 雙層藥型罩EFP速度理論模型

1.1 雙層藥型罩EFP裝藥結構

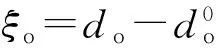
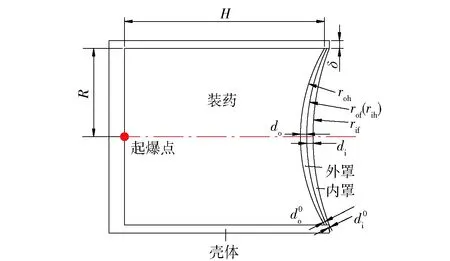
圖1 雙層藥型罩裝藥結構示意圖Fig.1 Structure of double liner shaped charge

根據文獻[9]，雙層藥型罩受裝藥爆轟驅動初期內外兩層罩始終貼合在一起，當作單層罩來考慮，等效單罩微元同時受裝藥軸向驅動及徑向壓縮作用(如圖2所示)。為推導雙層藥型罩形成的EFP速度計算模型，作如下假設：

1)假設瞬時爆轟，不考慮起爆位置影響；

2)藥型罩微元受爆轟波驅動，軸向速度未達到最大前內外雙罩不分離，按等體積原則當等效單罩處理；

3)藥型罩微元受爆轟波驅動，軸向速度達到最大后，內外罩受裝藥爆轟徑向作用徑向壓垮導致雙層藥型罩微元軸向發生碰撞和動量交換，導致內外雙罩分離；

4)藥型罩材料為剛塑性模型，動態屈服強度為定值；

5)EFP成形后徑向速度為0 m/s，軸向速度即為最終速度。

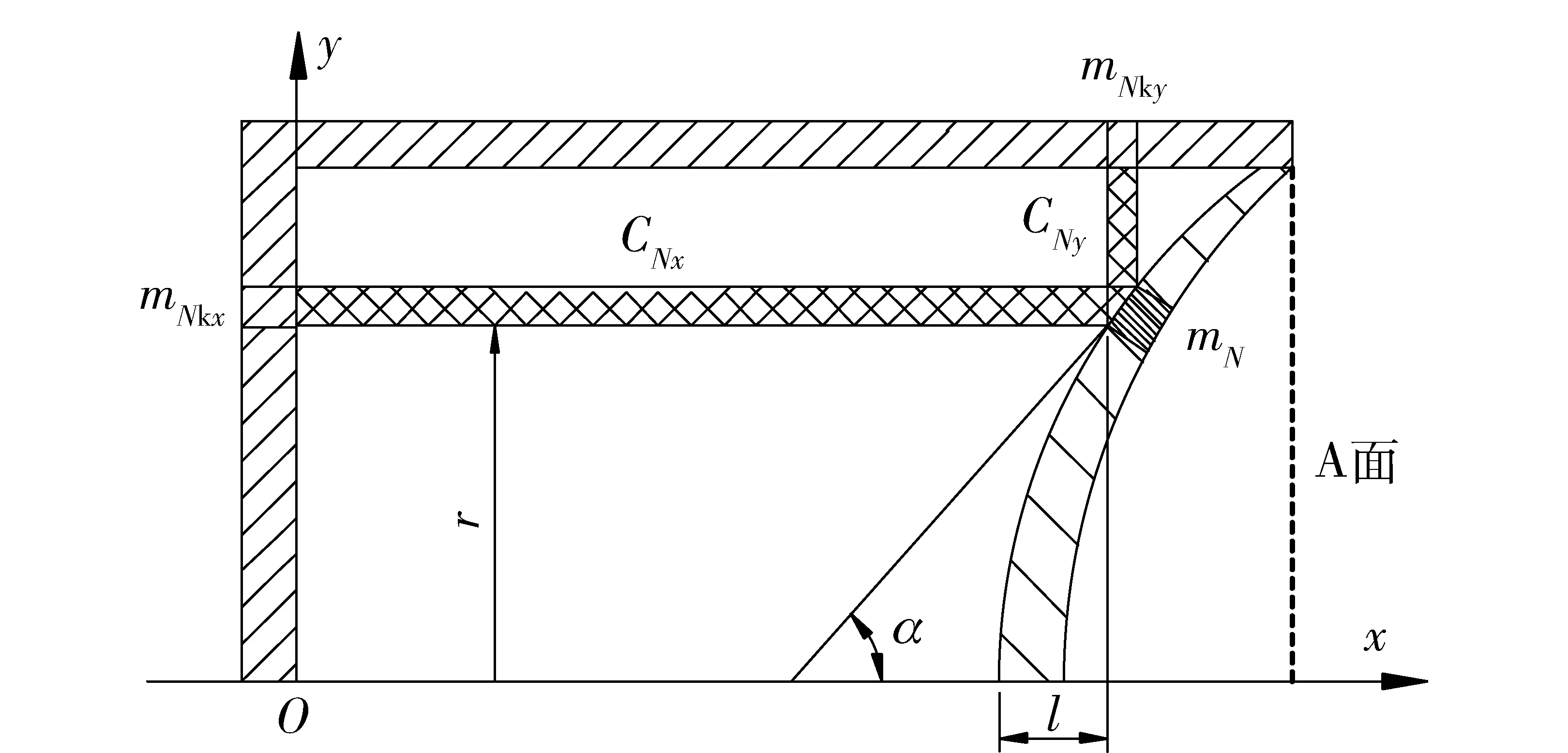
圖2 等效罩受裝藥軸向裝藥徑向裝藥作用示意圖Fig.2 Effect of explosive driving on liner element

1.2 等效單罩微元速度模型

圖2為等效單罩微元N受軸向、徑向裝藥驅動示意圖。罩微元徑向位置為r，距罩頂距離為l.CNx為罩微元所對應軸向裝藥質量，CNy為罩微元所對應徑向裝藥質量，mN為罩微元質量，mNkx為罩微元所對應軸向殼體微元質量，mNky為罩微元所對應徑向殼體微元質量。A面為罩底與裝藥軸線垂直面。

1.2.1 等效單罩微元軸向速度

經炸藥爆轟驅動平板Gurney公式[10]可得等效單罩微元N的軸向極限速度為

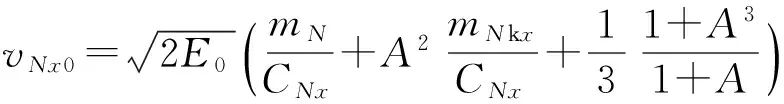
(1)

等效單罩微元質量[7]為

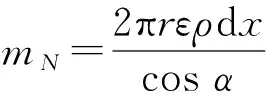
(2)

式中：ρ為等效單罩密度；ε為r處雙層藥型罩厚度；α為罩微元N切線處與x軸夾角。

根據有效裝藥理論，圓柱裝藥對大錐角、球缺罩的爆轟驅動可簡化為等效平板驅動模型[11]。考慮裝藥徑向膨脹引起的軸向能量輸出損失，藥型罩微元N的軸向速度[12]為

vNx=vNx0cos (0.766 8r/R)·

(1-0.376 1e(-0.720 7δ/(2R))(H/(2R))0.466 4).

(3)

1.2.2 等效單罩微元徑向速度

由炸藥驅動圓筒向內壓垮計算公式[13]可得藥型罩微元N的徑向極限速度為

(4)

式中：r0是炸藥內虛擬剛壁(即炸藥爆轟產物速度為0 m/s處)半徑。

對于球缺罩，罩微元被壓垮到軸線或A面處時已不受炸藥徑向壓縮作用，無法被驅動到徑向最大速度，等效罩微元徑向速度[10]為

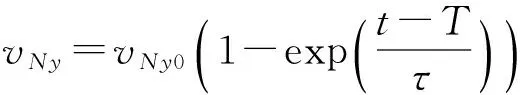
(5)

式中：T為爆轟波到達微元的時間；t為罩微元運動到軸線處時間或運動到A面處時間的最小值；τ為時間常數。

1.3 雙層藥型罩內外罩微元速度模型

根據假設3，爆轟波驅動罩微元后期，內外藥型罩微元發生碰撞和動量交換，導致內外罩分離。

1.3.1 內外罩微元徑向速度模型

藥型罩微元爆轟加載下向內壓垮，罩微元內表面壓合速度高于外表面壓合速度。等效單罩微元N內外表面徑向壓垮速度[14]為

vNyh=2vNy/(k+1),

vNyf=vNyh(1+1/((rNy/rN0)2-1))0.5,

(6)

式中：vNyh為等效單罩微元N靠近炸藥表面徑向壓垮速度；vNyf為等效單罩遠離炸藥表面徑向壓垮速度；rN0為等效單罩N壓垮到軸線后微元半徑。

等效單罩微元N對應內外罩微元徑向速度為

vNyo=(((1-n)vNyh+nvNyf+vNyh))/2，

(7)

vNyi=((1-n)vNyf+nvNyh+vNyf)/2，

(8)

式中：vNyo為外罩微元徑向壓垮速度；vNyi為內罩微元徑向壓垮速度；n為外罩微元與內罩微元厚度比。

1.3.2 內外罩微元軸向速度模型

定義藥型罩微元靠近裝藥一側為微元后端，遠離裝藥一側為微元前端。根據能量守恒定律，雙層藥型罩微元徑向動能除用于徑向壓縮塑性變形消耗外，其余全部轉化成為軸向的動能。由于罩微元徑向壓垮帶來的額外軸向速度，外罩微元前端速度大于內罩微元后端速度，內外罩微元發生碰撞而產生動量交換，從而導致內外罩所形成的EFP由于軸向速度差而發生分離。罩微元由于徑向壓縮引起的軸向速度變化[9]為

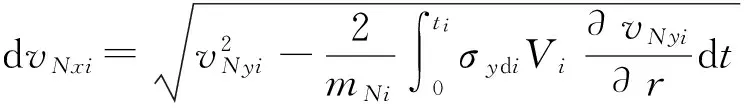
(9)

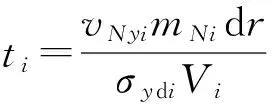
式中：i=i，o分別代表內外罩；ti為i罩微元徑向速度為0 m/s的時刻；σydi為i罩微元材料屈服強度；Vi為i罩微元體積；mNi為i罩微元質量；vNxi為i罩微元軸向速度。

罩微元前后端軸向速度為

(10)

式中：vNxih、vNxif分別為i罩微元內前后端軸向速度。

假定碰撞后外罩前端軸向速度與內罩后端軸向速度最終一致為

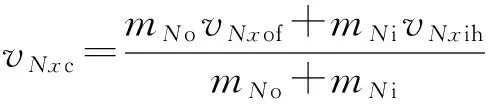
(11)

外罩、內罩微元最終軸向速度為

(12)

內外罩EFP最終速度為

(13)

由上述理論推導可知，外罩EFP與內罩EFP之間存在軸向速度差，不考慮速度衰減，常規等口徑雙層藥型罩串聯EFP飛行一定距離后會發生分離。

基于球缺藥型罩所建立的雙層EFP速度模型可擴展應用于大錐角藥型罩或球缺- 大錐角藥型罩組合雙層EFP速度計算。

2 算例及結果分析

為驗證所推導雙層EFP速度計算模型準確性，采用LS-DYNA軟件對圖1所示裝藥結構進行雙層EFP成型數值模擬。EFP結構模型為：鋼殼厚δ=0.09R，裝藥長徑比H/R=2，銅制內外罩頂總厚為0.1R，藥型罩壁厚差ξo/do=ξi/di=0.3. 裝藥選用JH-2炸藥，密度1.72 g/cm3.

數值模型中的殼體及炸藥均采用Lagrange算法。藥型罩采用自適應網格方法，并適時使用重啟動方法刪除炸藥和殼體網格。

圖3為計算模型所得等效單罩徑向速度隨外罩曲率變化示圖，圖4為計算所得等效罩微元徑向速度隨位置變化曲線圖。由圖3和圖4可知，等效罩微元徑向壓垮速度隨徑向位置增加先增加、后減小，隨罩曲率半徑增大而減小。這主要是因為隨罩微元徑向位置及罩曲率半徑增加，罩微元到罩底端距離減小，受徑向裝藥驅動時間減小，因而徑向壓垮速度發生如圖3和圖4所示變化。

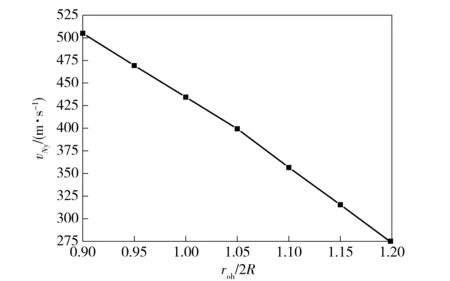
圖3 等效單罩徑向速度隨外罩曲率變化圖Fig.3 Radial velocity of equivalent liner element vs. roh/2R

圖4 等效罩微元徑向速度隨位置變化圖Fig.4 Radial velocity of equivalent liner element vs. r/R

圖5為雙層EFP軸向速度隨曲率變化計算模型與數值模擬結果對比圖。由理論分析可知，相同徑向位置處罩微元徑向壓垮帶來的額外軸向速度隨外罩曲率增加而減小。故由圖5可知，隨外罩曲率增加，外罩EFP軸向速度增加，內罩EFP軸向速度衰減，內外罩EFP軸向速度差減小，有利于形成頭尾相連大長徑比的串聯EFP. 計算模型所得結果與數值模擬結構吻合較好，最大誤差不超過5%.

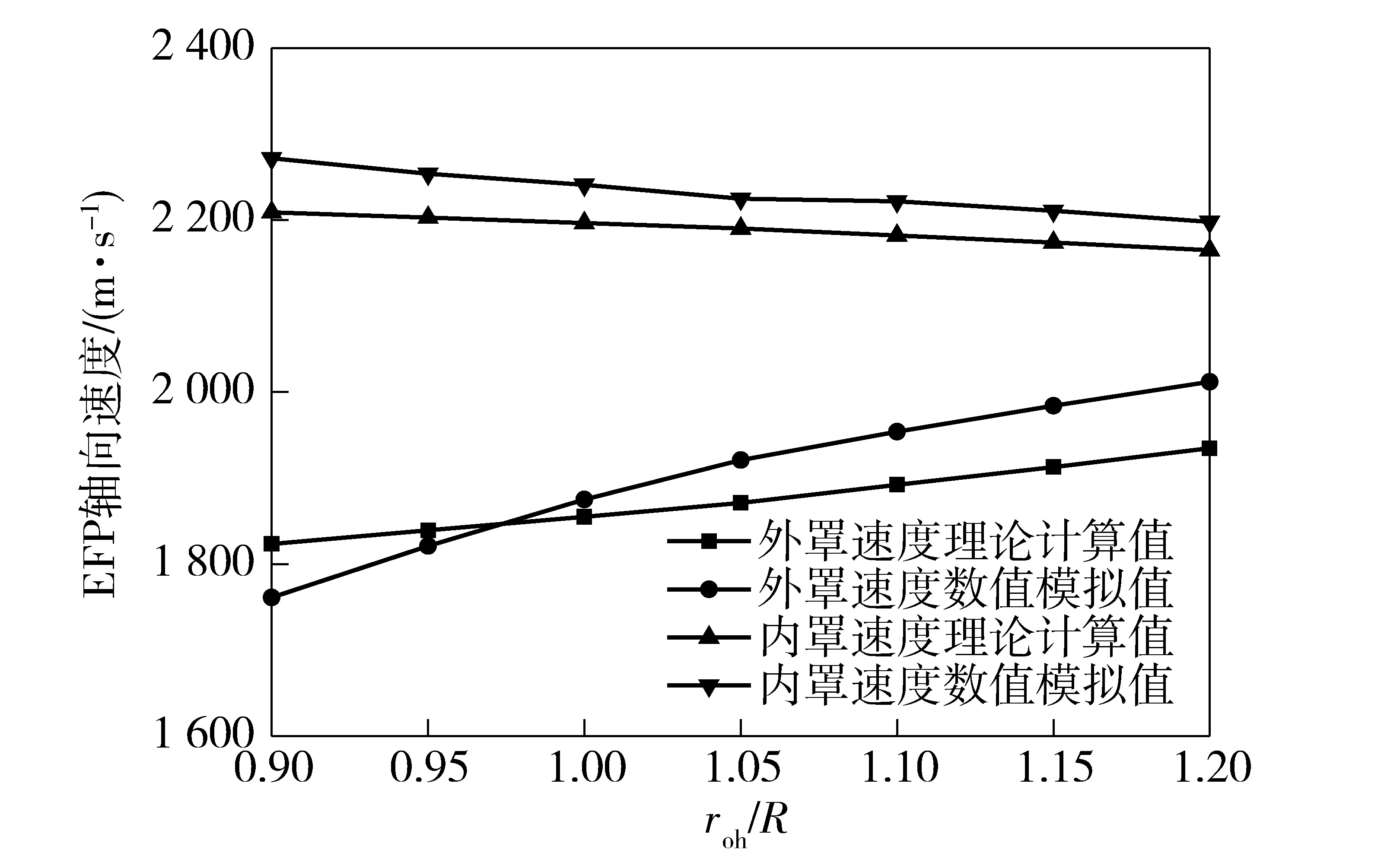
圖5 雙層EFP軸向速度隨曲率變化圖Fig.5 Axial velocities of tandem EFP vs. roh/R

圖6為雙層EFP軸向速度隨外罩厚度變化圖(roh=2R)。由理論分析可知，內外罩微元碰撞后外罩微元前端軸向速度與內罩微元后端軸向速度隨外罩厚度增加而增加。故由圖6可知，內外罩所形成EFP軸向速度均隨外罩所占厚度比增加而增加。計算模型所得結果與數值模擬結構吻合較好，最大誤差不超過6%.

圖6 雙層EFP軸向速度隨外罩厚度變化圖Fig.6 Velocities of tandem EFP vs. do/(do+di)

3 試驗驗證

為驗證上述理論計算模型及數值模擬結果，采用圖1所示裝藥結構開展雙層藥型罩EFP成型脈沖X光驗證試驗。表1為試驗工況表。

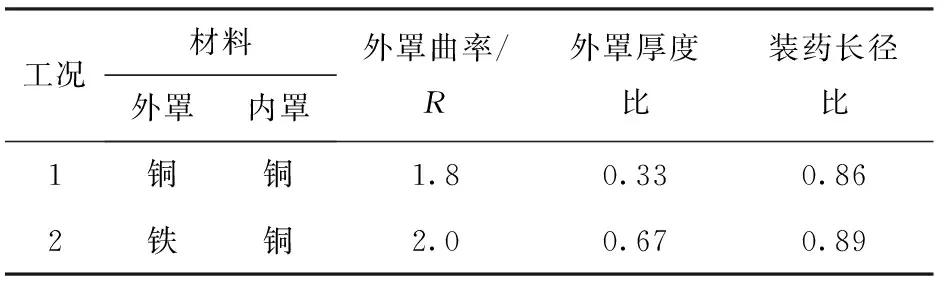
表1 脈沖X光雙層藥型罩EFP成型試驗方案表

表2和表3為起爆后不同時刻雙層EFP脈沖X光試驗與數值模擬結果的對比表。表4和表5為脈沖X光雙層藥型罩EFP軸向速度對比表。雙層EFP脈沖X光成型結果與數值模擬結果吻合較好，計算模型、數值模擬及試驗所得雙層EFP內外罩速度基本一致，表明本文所采用的數值模擬方法及其所驗證理論模型是可靠的。

表2 雙層EFP成型X光試驗與數值模擬結果對比表(工況1)

Tab.2 Comparison of X-ray test and simulated double-layer liner EFP formation results in Condition 1

表3 雙層EFP成型X光試驗與數值模擬結果對比表(工況2)

表4 雙層藥型外罩EFP速度對比表

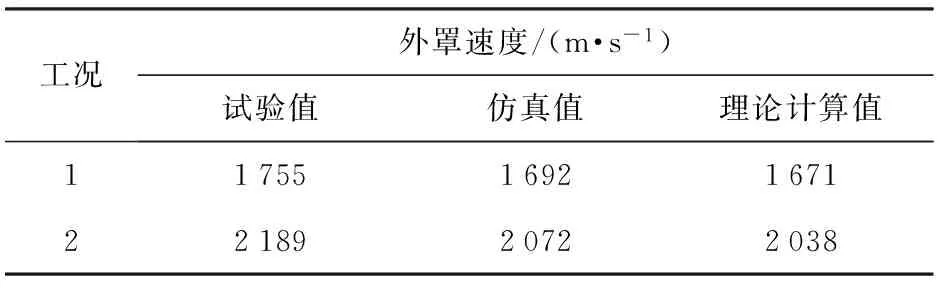
工況外罩速度/(m·s-1)試驗值仿真值理論計算值11755169216712218920722038

表5 雙層藥型內罩EFP速度對比表

4 結論

基于藥型罩微元爆轟驅動及碰撞理論建立了雙層藥型罩串聯EFP速度計算模型。通過計算及分析得到以下結論：

1)雙層藥型罩串聯EFP速度計算模型與數值模擬及試驗結果吻合較好，分析模型與數值模擬結果最大誤差不超過6%，能夠較好描述裝藥結構參數對串聯EFP速度影響規律。

2)藥型罩微元徑向壓垮引起的內外罩EFP軸向速度差是串聯EFP分離的核心因素。徑向壓垮速度隨藥型罩曲率增加而減小，常規等口徑雙層藥型罩結構內罩EFP與外罩EFP之間存在軸向速度差。

3)隨外罩曲率增加，罩微元徑向速度減小，外罩EFP軸向速度增加，內罩EFP軸向速度衰減，有利于形成頭尾相連大長徑比的串聯EFP。

4)裝藥長徑比、殼厚、曲率等因素一定的條件下, 隨外罩所占厚度比增加，內罩EFP、外罩EFP軸向速度增加。

References)

[1] Weimann K, Blache A. An explosively formed projectile with tantalum penetration and steel stabilization base[C]∥Proceedings of the 18th International Symposium on Ballistics. San Antonio, TX, US: IBC,1999:22-25.

[2] Fong R, Weimann K. Testing and analysis of multi-liner EFP warheads[C]∥Proceedings of the 20th International Symposium on Ballistics. Orlando, FL, US:IBC, 2002:578-582.

[3] 鄭宇, 王曉鳴, 李文彬. 基于雙層藥型罩成型裝藥的串聯EFP[J]. 爆炸與沖擊, 2012, 32(1):29-33. ZHENG Yu, WANG Xiao-ming, LI Wen-bin. Formation of shaped charge with double layer liners into tandem EFP[J]. Shock and Waves, 2012, 32(1):29-33.(in Chinese)

[4] 鄭宇, 王曉鳴, 李文彬, 等. 曲率半徑對雙層球缺罩形成串聯爆炸成型彈丸的影響[J]. 高壓物理學報, 2009, 23(3):33-38. ZHENG Yu, WANG Xiao-ming, LI Wen-bin, et al. Effects of liner curvature radius on formation of double-layered spherical segment charge liner into tandem explosively formed projectile (EFP)[J]. Chinese Journal of High Pressure Physics, 2009, 23(3):33-38. (in Chinese)

[5] 鄭宇, 王曉鳴, 李文彬. 材料對雙層藥型罩形成串聯EFP的影響[J]. 兵器材料科學與工程, 2009, 32(1):38-41. ZHENG Yu, WANG Xiao-ming, LI Wen-bin. Effects of materials on formation of double-layer shaped charges into tandem EFP[J]. Ordnance Material Science and Engineering, 2009, 32(1):38-41. (in Chinese)

[6] 劉健峰, 龍源, 紀沖, 等. 不同藥型罩壁厚組合影響同軸EFP成型規律研究[J]. 工程爆破, 2012, 18(4):9-13. LIU Jian-feng, LONG Yuan, JI Chong, et al. Influence of different wall-thickness combinations of arc-cone liner on coaxial EFP forming law[J]. Engineering Blasting, 2012, 18(4):9-13. (in Chinese)

[7] 劉健峰, 毛振興, 龍源, 等. 曲率半徑對雙層藥型罩EFP戰斗部成型及侵徹的影響[J]. 爆破器材, 2016,45(3):5-10. LIU Jian-feng. MAO Zhen-xing, LONG Yuan, et al. Influence of curvature radius on the formation and penetration of explosively formed penetrator warhead of the double layer liner[J]. Explosive Materials, 2016, 45(3):5-10. (in Chinese)

[8] 劉健峰, 龍源, 紀沖, 等. 雙層藥型罩EFP戰斗部性能參數的灰色系統理論分析及實驗研究[J]. 含能材料, 2016, 24(8): 728-734. LIU Jian-feng, LONG Yuan, JI Chong, et al. Theoretical and experimental study on performance parameters of double layer liners EFP warhead based on grey system theory[J]. Chinese Journal of Energetic Materials, 2016, 24(8): 728-734. (in Chinese)

[9] 鄭宇. 雙層藥型罩毀傷元形成機理研究[D]. 南京:南京理工大學, 2008. ZHENG Yu. Study on the formation mechanism of kill element from shaped charge with double layer liners[D]. Nanjing:Nanjing University of Science and Technology, 2008. (in Chinese)

[10] 隋樹元, 王樹山, 終點效應學[M]. 北京: 國防工業出版社, 2000. SUI Shu-yuan, WANG Shu-shan. Terminal effects[M]. Beijing: National Defense Industry Press, 2000. (in Chinese)

[11] 林加劍. EFP成型及其終點效應研究[D]. 合肥:中國科學技術大學, 2009. LIN Jia-jian. Research on the formability of EFP and its terminal effect[D].Hefei: University of Science and Technology of China, 2009.(in Chinese)

[12] Jiang J W, Feng S S, Men J B. Simplified approach to velocity of axial forward projection fragments from the end of warhead[J]. Journal of Beijing Institute of Technology, 2004, 13(4):402-405.

[13] Chou P C, Carleone J, Hirsch E, et al. Improved formulas for velocity, acceleration and projection angle of explosively driven liners[C]∥Proceedings of the 6th International Symposium on Ballistics. Orlando, FL, US: IBC, 1981.

[14] 夏杰.雙層藥型罩射流形成的理論研究與數值模擬[D]. 武漢:武漢科技大學, 2012. XIA Jie. The theoretical research and numerical simulation on jet formation of double-layer liner[D]. Wuhan:Wuhan University Science and Technology, 2012. (in Chinese)

A Calculation Model of Velocity of Tandem EFP with Double Layer Liners

WANG Zhe, JIANG Jian-wei, WANG Shu-you, REN Rei-chi

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

A velocity calculation model of tandem EFP is proposed by analyzing the motion of elements in double-layer liners. The analysis shows that the difference in EFP axial velocities caused by radial velocity plays an important role in the separation of the tandem EFP. The velocity of EFP formed by outside liner increases with the increase in the curvature of outside liner and the thickness ratio of outside liner to inside liner. On the other hand, the velocity of EFP formed by inside liner decreases with the increase in curvature of outside liner, but increases with the increase in thickness ratio of outside liner to inside liner. The calculated results agree well with experimental data and simulated results by LS-DYNA.

ordnance science and technology; explosion; tandem EFP; double layer liners; velocity

2016-11-11

爆炸科學與技術國家重點實驗室自主課題探索性項目(QNKT16-01)；國家國防科技工業局技術基礎科研項目(B2620110006)

王哲(1989—)，男，博士研究生。E-mail:994353449@qq.com

蔣建偉(1962—)，男，教授，博士生導師。E-mail:bitjjw@bit.edu.cn

TJ410.3+33

A

1000-1093(2017)07-1301-06

10.3969/j.issn.1000-1093.2017.07.007