彈丸批質量水平的密集度檢驗方法

繆云飛, 徐榕， 王國平, 陳東陽, 贠來峰, 戰志波

(1.南京理工大學 能源與動力工程學院, 江蘇 南京 210094; 2.陸軍重慶軍事代表局, 重慶 400000； 3.陸軍南京軍事代表局, 江蘇 南京 250031)

彈丸批質量水平的密集度檢驗方法

繆云飛1, 徐榕2， 王國平1, 陳東陽1, 贠來峰3, 戰志波3

(1.南京理工大學 能源與動力工程學院, 江蘇 南京 210094; 2.陸軍重慶軍事代表局, 重慶 400000； 3.陸軍南京軍事代表局, 江蘇 南京 250031)

彈丸批質量水平的密集度檢驗方法是考核彈丸批生產質量的重要手段。為了探索新型彈丸批質量水平的密集度檢驗方法，基于計算流體力學軟件和經驗公式的彈丸空氣動力學參數快速仿真計算方法，分析彈丸的結構誤差對氣動參數的影響，建立了彈丸氣動參數數據庫。以Visual Basic為平臺，建立了考慮質量偏心、動不平衡、射角、質量、彈道風等因素的彈丸數學模型，開發了火炮彈丸密集度仿真軟件并進行驗證。基于仿真軟件，進行了隨機因素與密集度的相關性分析，得到彈質量、彈徑、質量偏心、動不平衡、初始擺動角、初始擺動角速度和初速對高低密集度和方位密集度影響程度的大小順序，給出了彈丸批質量水平密集度檢驗方法的流程及應用。研究結果表明，該密集度檢驗方法在彈丸批質量水平的考核中是可行的。

兵器科學與技術； 彈丸； 氣動參數； 結構誤差； 密集度

0 引言

現代戰爭對武器系統提出了越來越高的要求，武器的精度直接關系到戰爭的主動權甚至是戰爭的勝利，因此發展精確打擊彈藥是軍界和軍火工業界的共識[1]。在彈丸生產制造過程中，由于設備、工藝以及技術水平等諸多因素的影響，導致同一批次彈丸彈體質量、質量偏心、外形結構等存在一定的偏差，這些彈丸的加工質量不一致性可能會對彈丸的氣動特性、飛行穩定性和射擊密集度帶來影響。而密集度是火炮發射過程中內彈道和外彈道等因素綜合影響的結果[2]，是最能體現彈丸加工質量不一致性的特征量。因此開展彈丸的結構誤差對射擊密集度影響的理論分析，開發考慮彈丸加工質量不一致性的密集度仿真軟件，建立彈丸批質量水平的密集度檢驗方法，從而為工廠生產和加工彈丸奠定理論基礎和技術支持十分必要。

近年來，隨著計算機應用的普及，根據射擊條件建立彈道程序，通過仿真計算代替部分實彈射擊試驗，已經成為研究隨機因素對彈丸精度影響的一種手段。劉鵬飛等[3]以ADAMS為動力學仿真工具，在Multigen視景仿真平臺上對武器系統的外彈道虛擬技術進行了研究，提出了一套系統的外彈道虛擬試驗方案，并進行了實例驗證。賴煜坤等[4]引入了基于接口的協同仿真技術，構建了參數化的自行火炮射擊密集度仿真平臺，實現了快速準確地計算自行火炮射擊密集度。張浩等[5]利用Maltab軟件，采用蒙特卡洛法和6自由度彈道方程建立了彈丸地面密集度仿真模型，研究分析了彈丸最大射程和非最大射程地面密集度的影響因素。

但是目前還沒有人提出將數值仿真研究與彈丸批質量水平的密集度檢驗有效地結合起來?；诖藛栴}，本文通過建立彈丸仿真模型，分析結構誤差對彈丸氣動特性的影響，建立彈丸的氣動參數數據庫。其次針對旋轉彈的發射情況，在考慮質量偏心、動不平衡、彈道風、質量等因素影響的彈丸6自由度剛體彈道模型基礎上，以Visual Basic 為平臺建立身管火炮彈丸密集度仿真軟件。然后，結合彈丸氣動參數數據庫和仿真軟件，依據相關性理論分析研究彈丸對射擊密集度影響的主要因素，最后結合工廠指標要求給出通過仿真軟件檢驗密集度來評定彈丸批質量水平的方法。

1 結構誤差對氣動參數的影響

本文以某旋轉彈丸為例，建立了3種幾何模型，即無誤差理論模型、質量偏心模型和不同軸模型，如圖1～圖3所示。

圖1 無誤差理論模型Fig.1 Theory model without structural error

圖2 質量偏心模型Fig.2 Model with mass eccentricity

圖3 不同軸模型Fig.3 Model with different concentricity

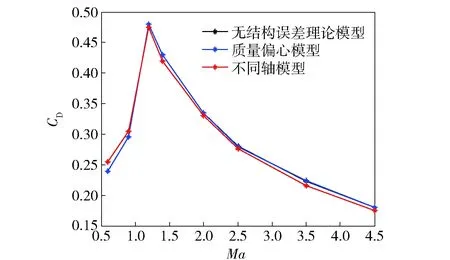
圖4 不同模型的阻力系數- 馬赫數曲線Fig.4 CD-Ma curves for different models

采用計算流體力學(CFD)軟件與工程經驗公式相結合的數值方法[6-7]來計算彈丸的氣動參數。計算結果如圖4～圖9所示，其中Ma、CD、CNα、Cmα、Clp、Cnpα、Xcp分別為馬赫數、阻力系數、法向力系數導數、俯仰力矩系數、滾轉阻尼系數、馬格努斯力矩系數導數、壓心系數。

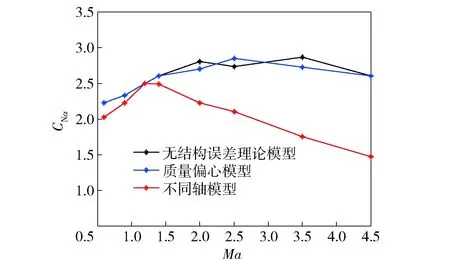
圖5 不同模型的法向力系數導數- 馬赫數曲線Fig.5 CNα-Ma curves for different models

圖6 不同模型的俯仰力矩系數- 馬赫數曲線Fig.6 Cmα-Ma curves for different models

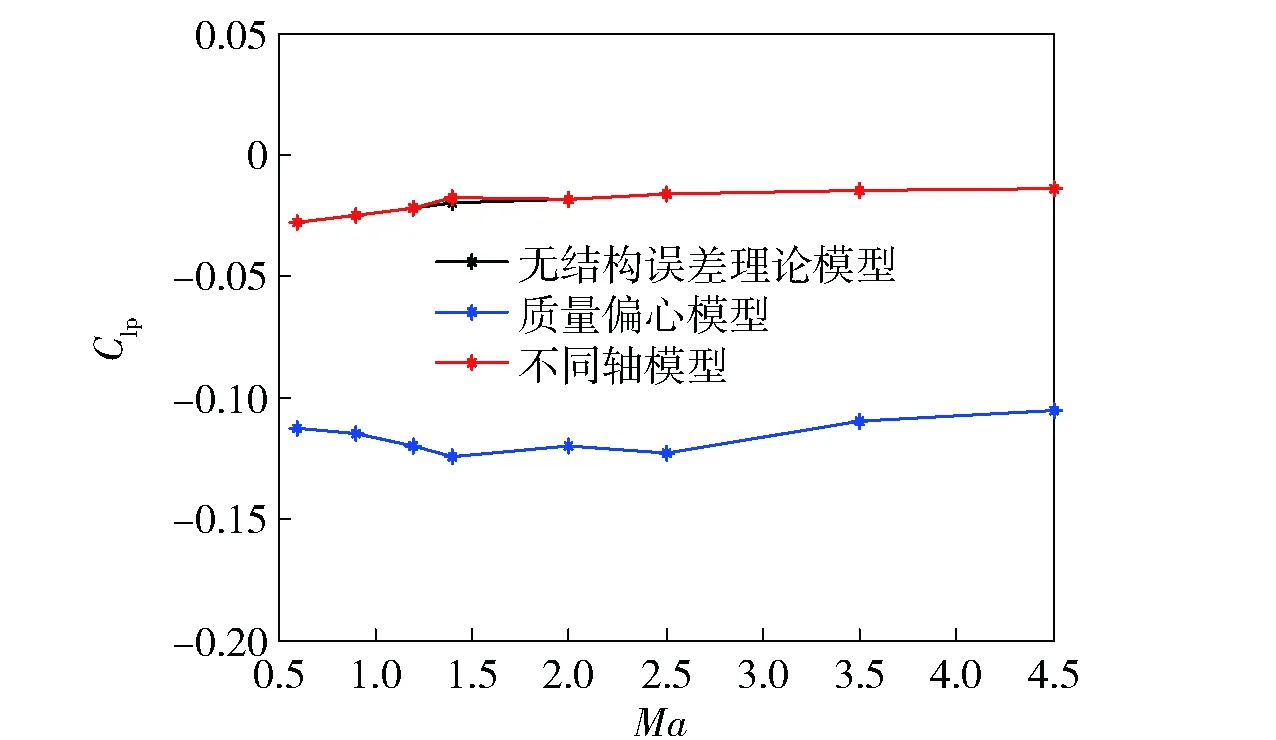
圖7 不同模型的滾轉阻尼系數- 馬赫數曲線Fig.7 Clp-Ma curves for different models

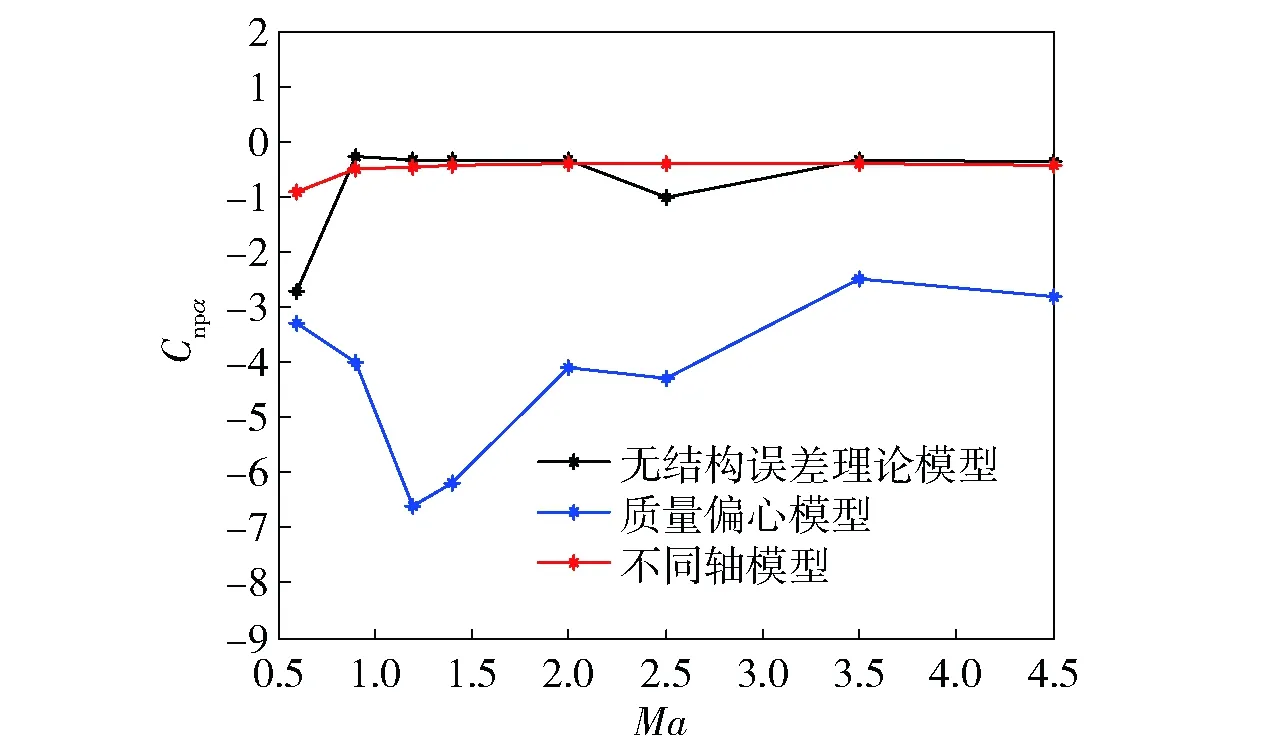
圖8 不同模型的馬格努斯力矩系數導數- 馬赫數曲線Fig.8 Cnpα-Ma curves for different models

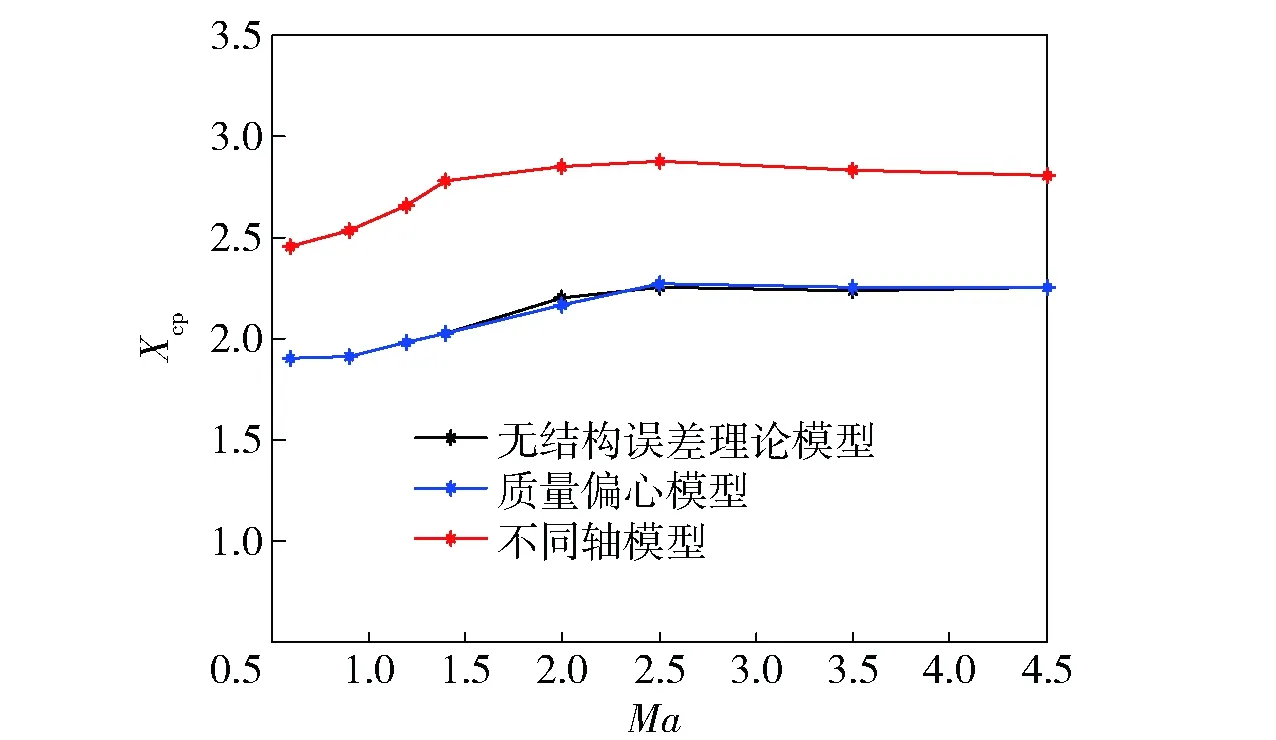
圖9 不同模型的壓心系數- 馬赫數曲線Fig.9 Xcp-Ma curves for different models

從圖4可以看出，質量偏心對計算模型的阻力幾乎沒有影響，說明阻力的大小只和模型外形有關，與質心偏移幾乎無關。不同軸模型在亞音速和跨音速部分，阻力系數比理論模型大，在超音速部分阻力系數比理論模型小。這是由于模型不同軸時，導致模型外形改變，摩阻、渦阻、波阻都有所改變所造成的。

圖5為3種模型的法向力系數導數隨馬赫數變化趨勢。對于質量偏心模型，導致旋轉軸線偏移，在亞音速和跨音速部分，計算結果和理論模型結果一致；在超音速時，使法向力系數導數相對理論模型的計算結果產生一些波動。由于不同軸模型的彈頭處攻角相對理論模型變小，從而導致法向力系數導數比理論模型計算結果小，并且隨著馬赫數的增大，法向力系數導數下降趨勢變大。質量偏心導致的旋轉軸偏移和不同軸導致的外形改變對彈的法向力有一定影響，尤其是外形的改變對法向力影響很大。

從圖6可以看出，不同軸模型對俯仰力矩系數導數影響很大，這是由于不同軸模型對法向力系數影響很大造成的。

從圖7可以看出，質量偏心導致旋轉軸偏移，從而導致滾轉阻尼系數變化很大。而不同軸導致的外形微小改變對滾轉阻尼系數幾乎沒有影響。

馬格努斯力矩的產生和攻角、旋轉有關。從圖8可以看出，不同軸導致的彈頭部攻角改變，和質量偏心導致的旋轉軸偏移，都會對馬格努斯力矩系數導數產生了較大影響，尤其是質量偏心的情況，對馬格努斯力矩影響更大，是馬格努斯力矩系數導數絕對值整體變大。

從圖9可以看出，主要是不同軸導致的彈體外形變化對壓心系數影響很大。

旋轉穩定彈飛行穩定性必須滿足陀螺穩定條件和動態穩定條件[8]。其中陀螺穩定因子與彈的幾何尺寸、飛行速度、自轉速度、極轉動慣量、赤道轉動慣量、俯仰力矩系數導數、馬格努斯力矩系數導數有關。動態穩定性條件與陀螺穩定因子、馬格努斯力矩系數導數、俯仰阻尼系數導數、阻力系數、法向力系數導數、彈道傾角、理想傾角、重力加速度有關。從本文計算結果發現，3種模型的馬格努斯力矩系數導數、俯仰力矩系數導數、法向力系數導數差異很大，所以結構誤差對旋轉彈的飛行穩定性必定造成很大影響。

2 考慮批質量水平的密集度仿真及驗證

2.1 仿真系統

彈丸發射與飛行過程中受多種隨機因素的影響，這些隨機因素包括：火炮、彈丸和裝藥系統參數的隨機變化，使用環境(氣象條件、地面條件等)和操作過程(人員技術素質、操作誤差等)的隨機性等。確定性模型對系統問題分環節孤立處理，難以獲得滿意的分析結果，所以本文采用的是隨機模型和試驗測量相結合的模擬彈丸批質量水平仿真的方法。理論計算與試驗結果表明，影響彈丸密集度的因素來源于3個方面：彈丸的彈道參數、空氣動力學參數和彈丸特征參數[9]。其中，彈丸外彈道起始擾動數據由文獻[10]中的方法計算得到，彈丸的結構參數采用實測值，空氣動力學參數采用CFD數值計算?；谏鲜隹紤]的因素，先利用CFD數值模擬得到不同結構誤差的彈丸氣動參數，作為軟件的數據庫，采用文獻[7]中精確的剛體彈丸運動方程組，基于Visual Basic編程平臺建立了彈丸密集度批質量水平仿真軟件，該軟件包含主界面、操作界面、彈道曲線和彈著點散布界面4個模塊。圖10是軟件的界面，仿真軟件參數輸入的模塊如圖11所示。

圖10 仿真軟件界面Fig.10 Interface for simulation software

圖11 參數輸入界面Fig.11 Interface for reading parameters

2.2 仿真驗證

利用試驗中彈丸結構參數的實測值和數值仿真得到的氣動力參數，輸入到密集度批質量彈丸仿真軟件進行密集度計算。

表1給出了7發落點散布的仿真結果，表2中給出了1 000 m立靶密集度仿真結果。從1 000 m立靶密集度的計算值與以往的試驗值相比，誤差在合理的范圍之內，初步驗證了仿真系統的正確性。

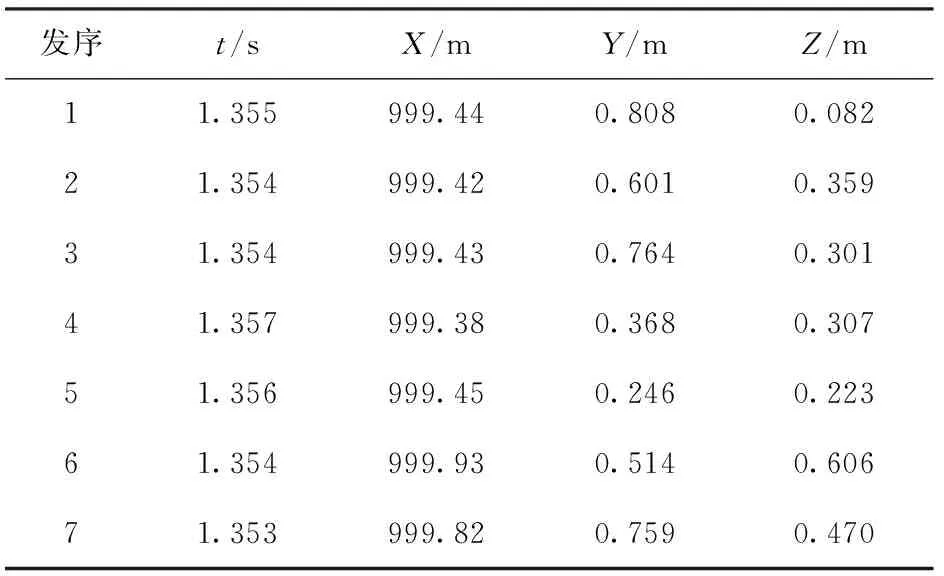
表1 7發彈丸的1 000 m立靶彈著點

表2 1 000 m立靶密集度仿真結果誤差

為了進一步驗證仿真系統的正確性，根據兩組試驗測得的參數，如表3所示，進行仿真計算。計算結果與實際射擊試驗結果如表4所示，進一步驗證了仿真軟件的正確性。

表3 彈丸炮口初速和風速的試驗結果

表4 1 000 m立靶密集度仿真與試驗結果誤差

3 批質量水平與密集度的相關性分析

基于文獻[11]中的相關性分析理論，根據彈丸隨機變量的均值和均方差與射擊密集度之間相關系數的絕對值及其相關性檢驗統計量的絕對值相對大小，判斷彈丸各隨機變量均值和均方差與密集度之間的相關程度，從而確定影響射擊密集度的主要隨機擾動因素。在研究質量偏心、動不平衡、彈質量、彈徑、初速、初始擺動角速度以及初始擺動角等因素與密集度的相關性時，采取控制變量法，計算它們之間的相關系數。根據仿真結果，得到質量偏心與高低密集度和方位密集度的相關系數分別為0.090 0和0.244 8，動不平衡與高低密集度和方位密集度的相關系數分別為0.308 6和0.485 1，彈徑與高低密集度和方位密集度的相關系數分別為-0.007 4和0.104 0，彈質量與高低密集度和方位密集度的相關系數分別為0.615 7和0.407 0，初速與高低密集度和方位密集度的相關系數分別為-0.184 5和0.236 3，側向擺動角與高低密集度和方位密集度的相關系數分別為0.131 2和-0.231 5，鉛垂擺動角與高低密集度和方位密集度的相關系數分別為-0.528 8和-0.439 0，側向擺動角速度與高低密集度和方位密集度的相關系數分別為0.432 8和0.521 6，鉛垂擺動角速度與高低密集度和方位密集度的相關系數分別為0.658 2和0.456 3. 由此可見，影響密集度程度比較高的因素是彈質量和初始擺動角速度，彈徑對密集度的影響程度相對較低。初步判斷出各影響因素對彈丸射擊密集度影響程度按從大到小排列為：

高低密集度：鉛垂擺動角速度>彈質量>鉛垂擺動角>側向擺動角速度>動不平衡>初速>側向擺動角>質量偏心>彈徑

方位密集度：側向擺動角速度>動不平衡>鉛垂擺動角速度>鉛垂擺動角>彈質量>質量偏心>初速>側向擺動角>彈徑。

由于工廠加工彈丸關注更多的是彈丸本身的特征參數，所以應該重點關注的順序為彈質量、動不平衡、質量偏心和彈徑。

4 彈丸批質量水平的密集度檢驗流程及應用

根據某彈丸的密集度指標，應用建立的仿真軟件評價彈丸批質量水平的密集度是否滿足指標的整個在線模擬過程如下：

1) 運行軟件，進入在線模擬。

2) 在軟件中讀入彈丸的初始條件，輸入需要測量的參數。

3) 輸入批質量彈丸需要計算的發數和計算方案，得到該組的密集度。密集度大于指標要求的給定為不合格；小于指標要求(即合格)的條件下，再根據仿真結果與指標之間的誤差來評判彈丸批質量水平為滿足指標(0～10%)、優于指標(10～30%)還是大大優于指標(>30%)，如表5～表7所示。

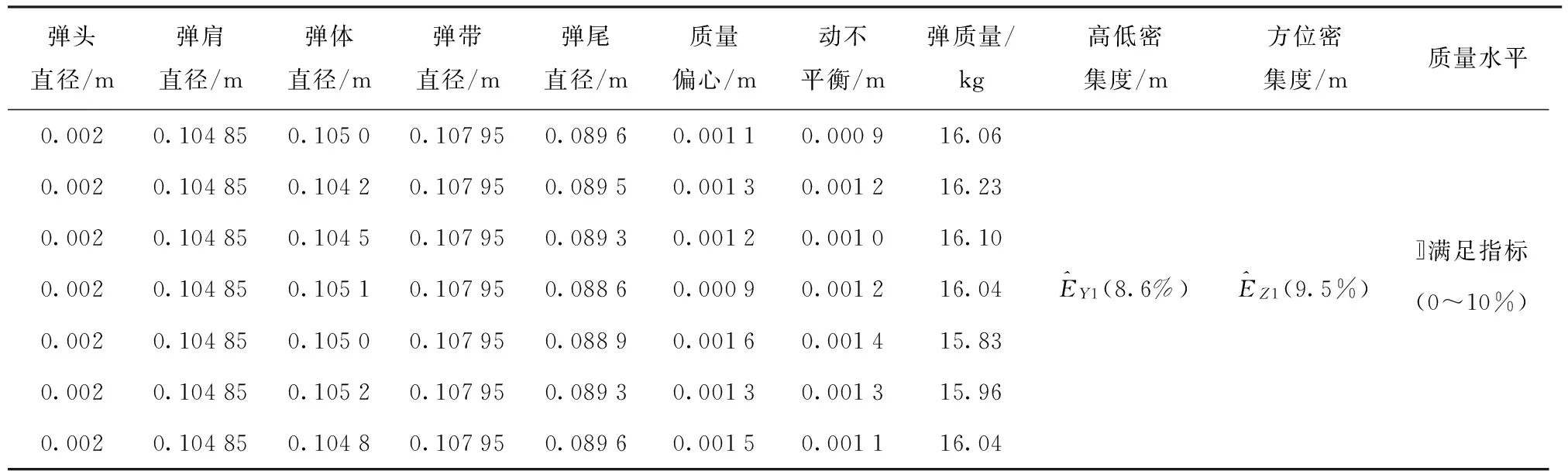
表5 第1組彈丸批質量水平的密集度檢驗(滿足指標)

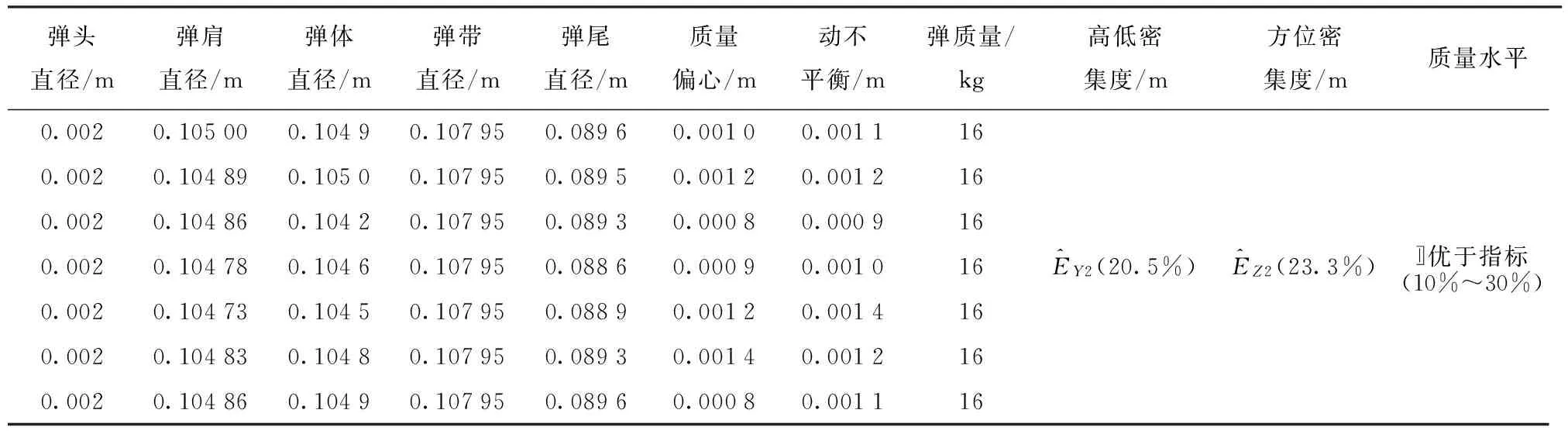
表6 第2組彈丸批質量水平的密集度檢驗(優于指標)

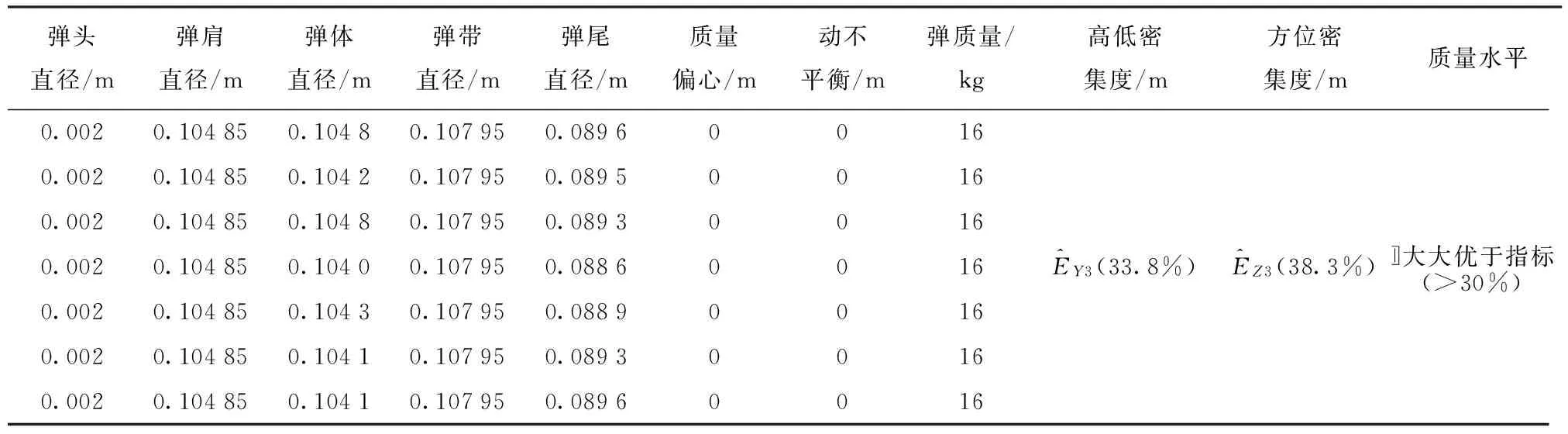
表7 第3組彈丸批質量水平的密集度檢驗(大大優于指標)

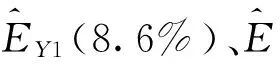
4) 如需檢驗下一批次的彈丸質量水平的密集度，重復2～3步。

5 結論

本文采用CFD數值模擬和工程經驗公式相結合的仿真技術，對某旋轉彈的不同結構進行了氣動參數仿真計算，仿真結果表明3種模型的馬格努斯力矩系數導數、俯仰力矩系數導數、法向力系數導數差異很大，因此結構誤差對旋轉彈的飛行穩定性必定造成很大影響。通過理論計算和試驗數據的對比驗證了彈丸密集度批質量水平仿真技術的正確性。通過研究質量偏心、動不平衡、彈徑、彈質量、初速、初始擺動角速度和初始擺動角7種因素與密集度的相關性，得到了各影響因素與彈丸射擊密集度的相關性程度的大小。最后，以工廠某旋轉彈密集度指標為例，給出了彈丸批質量水平的檢驗方法。本文研究成果可為工廠彈丸批質量的加工和批質量水平評價提供理論參考。

References)

[1] 譚鳳崗. 彈道修正彈的概念研究[J]. 彈箭技術, 1998(4):1-10. TAN Feng-gang. Concept development of trajectory correction projectiles[J]. Projectile & Rocket Technology, 1998(4):1-10. (in Chinese)

[2] 王寶元. 中大口徑火炮射擊密集度研究綜述[J]. 火炮發射與控制學報, 2015, 36(2):82-87. WANG Bao-yuan. Review of research on firing dispersion of medium and large caliber artillery [J]. Journal of Gun Launch & Control, 2015, 36(2):82-87.(in Chinese)

[3] 劉鵬飛, 馮順山, 曹紅松,等. 外彈道虛擬試驗技術的研究[J]. 彈箭與制導學報, 2015, 35(4):121-124. LIU Peng-fei, FENG Shun-shan, CAO Hong-song, et al. The research on technology of virtual trajectory experiment [J] .Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35 (4): 121-124.(in Chinese)

[4] 賴煜坤, 徐禮, 溫輝,等. 自行火炮射擊密集度仿真平臺[J]. 兵工自動化, 2015, 34(6):30-32. LAI Yu-kun, XU Li, WEN Hui, et al. Self-propelled gun fire intensity simulation platform[J]. Ordnance Industry Automation, 2015, 34(6):30-32.(in Chinese)

[5] 張浩, 聞泉, 王雨時,等. 炮彈地面密集度性能與射程關系仿真[J]. 彈道學報, 2016, 28(1):56-59. ZHANG Hao, WEN Quan, WANG Yu-shi, et al. Simulation research of relationship between ground dispersion performance of projectiles and firing range[J]. Journal of Ballistics, 2016, 28(1):56-59.(in Chinese)

[6] 陳東陽, Laith K.Abbas, 芮筱亭, 等. 結構誤差對旋轉穩定彈丸氣動特性影響的數值模擬計算[J]. 空氣動力學學報, 2014, 32(5): 705-711. CHEN Dong-yang, Abbas L K, RUI Xiao-ting, et al. Numerical simulation study of vehicle's aerodynamic characteristics effected by structure errors[J]. Acta Aerodynamic Sinica, 2014, 32(5):705-711. (in Chinese)

[7] William L K, William A W, Peter A G, et al. Computational aeroheating predictions for X-34[J]. Journal of Spacecraft and Rockets, 1999, 36(2):179-188.

[8] 徐明友.火箭外彈道學[M].北京：國防工業出版社,1980:224-226. XU Ming-you. Exterior ballistics of rockets[M]. Beijing:National Defense Industry Press, 1980:224-226. (in Chinese)

[9] 宋丕極. 槍炮與火箭外彈道學[M]. 北京:兵器工業出版社，1992. SONG Pi-ji. Exterior ballistics of guns and rockets[M]. Beijing: Publishing House of Ordnance Industry, 1992.(in Chinese)

[10] 芮曉亭, 劉怡昕, 于海龍. 坦克自行火炮發射動力學[M]. 北京: 科學出版社, 2011. RUI Xiao-ting, LIU Yi-xin, YU Hai-long. Launch dynamics of tank and self-propelled artillery[M]. Beijing:Science Press,2011.(in Chinese)

[11] 芮筱亭, 王國平, 陸毓琪, 等. 多管火箭彈發射動力學仿真與試驗測試方法[M]. 北京: 國防工業出版社, 2003. RUI Xiao-ting, WANG Guo-ping, LU Yu-qi, et al. Simulation and test methods of launch dynamics of multiple launch rocket system[M]. Beijing: National Defense Industry Press,2003.(in Chinese)

Test Method for the Intensity of Lot Quality Level of Projectiles

MIAO Yun-fei1, XU Rong2, WANG Guo-ping1, CHEN Dong-yang1, YUN Lai-feng3, ZHAN Zhi-bo3

(1.School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China; 2.Army Chongqing Military Representative Bureau, Chongqing 400000, China; 3.Army Nanjing Military Representative Bureau, Nanjing 250031, Jiangsu, China)

The test method of the intensity of projectiles in batches is an important measure of assessing the quality level of projectiles. In order to seek a new test method, the influences of the structural errors of projectiles on the aerodynamic parameters are analyzed using a fast simulation calculation method based on the technology, combing the computational fluid dynamics (CFD) software and the empirical formula for calculating the aerodynamic parameters of projectiles. The database of aerodynamic parameters of projectiles is established. A simulation software based on the six degree-of-freedom model and the Visual Basic is programmed and validated for calculating the intensity of projectiles in batches. The order of influences of the mass, diameter, mass eccentricity, dynamic unbalance, initial swing angle, initial swing angular velocity and muzzle velocity on the intensity is achieved by analyzing the correlation between random factor and intensity. The process and application of the test method are proposed. The research results show that the proposed test method is available for the assessment of the quality level of projectiles in batches.

ordnance science and technology; projectile; aerodynamic parameter; structure error; intensity

2016-12-03

武器裝備預先研究項目(ZLA13176)； 國家自然科學基金項目(11472135)

繆云飛(1992—)，男，博士研究生。E-mail: myf_njust@163.com

王國平(1976—)，男，教授，博士生導師。E-mail: wgp1976@163.com

TJ012.3+6

A

1000-1093(2017)07-1307-07

10.3969/j.issn.1000-1093.2017.07.008