復平面上分形圖的生成及在紡織品上的應用

王淑緩,楊旭紅

(蘇州大學 現代絲綢國家工程實驗室，江蘇 蘇州 215123)

設計與產品

復平面上分形圖的生成及在紡織品上的應用

王淑緩,楊旭紅

(蘇州大學 現代絲綢國家工程實驗室，江蘇 蘇州 215123)

為了拓展分形圖在紡織圖案設計上的應用，探索紡織圖案設計的快捷方法，為設計者提供更豐富、新穎的設計素材。首先，根據復平面上分形圖的生成方法與程序編寫，運用編程軟件Visual Basic 6.0，分別研究復平面上Mandelbrot集與Julia集的生成方法，實現其可視化。然后通過改變迭代函數的形式得到一系列變化分形圖，結合圖像處理、平面設計軟件等對得到的分形圖進行紋樣設計和效果模擬，利用印花技術將分形紋樣應用于紡織品上。結果表明，基于分形圖的紡織圖案設計更加適應快捷、高效、多變的紡織生產模式。

復平面；分形；程序設計；可視化；圖案設計

紡織圖案設計在現代紡織品設計中占有主要地位，傳統的紡織圖案設計本質是依靠人腦構想來完成，通過紙、筆及繪圖軟件繪制而成，這種設計方法受人腦靈感的限制，并要求設計者具有專業的手繪功底，且耗時長，圖案呈現過程繁瑣，形成的紡織圖案形式單一，局限性大。因此，分形作為一種新型的圖形生成方法應運而生，分形圖具有獲得方法簡捷，圖形色彩絢麗、結構層次豐富等特點，通過函數形式變化得到的變化分形圖對紡織圖案設計具有一定的探究意義。

分形圖是一種以數學理論作為基礎，通過調整迭代函數、變化規則及顏色參數等數據進行編程設計，實現程序代碼的可視化，將枯燥的數據轉化為絢麗的圖形或圖像。由于分形圖生成原理，其具有極精細結構，若沒有源代碼分形圖將不易復制和拷貝。這種分形圖實現了分形幾何學與計算機圖形學的完美聯合，同時也是科學與藝術的融合，另外分形圖的美是不可估量的，為紡織圖案設計增添了新元素[1]。張聿等[2-3]運用計算機繪圖方法，探究了借助電子印花技術將可視化信息展現在織物上的可行性。蔡燕燕等[4-5]對Mandelbrot集與Julia集基礎分形圖在圖案設計上作了闡述。楊旭紅等[6]對分形信息的可視化及其在紡織紋樣設計中的應用作了初步探究。孫博文[1]已經對Mandelbrot集、Julia集的生成方法做了具體的說明和討論，因此本文主要利用復平面上分形圖在Visual Basic 6.0中的實現方法，通過改變迭代函數形式和參數而生成變化分形圖，將其保存為圖片形式。運用圖像處理軟件Photoshop進行二次設計，并將變化分形圖廣泛應用于紡織紋樣設計中。

1 復平面分形圖的生成原理

1.1 基本原理

復平面上的分形圖主要是指基于逃逸時間算法的分形圖，其原理為：令函數或映射y=f(x)作為某一變化規則，若給定初始值x=x0，則有y=f(x0)，將得到的y值記作x1，則x1=f(x0)，x1作為x的一個新值，則有y=f(x1)，同理將得到的y值記作x2，則x2=f(x1)。對xn=f(xn-1)進行n次迭代賦值，將得到一個序列x0,x1,x2,...,xn作為x的逃逸軌跡。逃逸軌跡包括內部收斂于某一個或幾個點及外部發散兩個部分，在電腦屏幕上，不同的逃逸區域用不同的顏色表現出來就得到了分形圖[6-7]。復平面上的分形主要包括Mandelbrot集(簡稱M集)和Julia集(簡稱J集)。

1.2 M集和J集迭代函數的變化及變化圖形的生成

1.2.1 M集迭代函數的變化及變化圖形的生成

M集是分形理論首創者曼德勃羅在1980年發現的，采用的是復平面上的二維迭代關系：

Z=Zm+C

(1)

式中：Z是復數變量，C是復常數量，m是冪指數。

設定初始的Z值，使C值在復平面的某個區域內有規律地變化，追蹤C值得到迭代收斂的序列點，并對點進行著色繪圖[8]。計算機繪圖的具體操作：首先根據復數運算原理，求得展開式；再對復數的實部和虛部進行分離；最后將其轉化成計算機語言，進行編程設計。

M集位于復平面中，根據計算機繪圖原理及繪圖步驟，Z=Zm+C的基本函數形式是m=2時，可得到如圖1(a)所示分形圖。

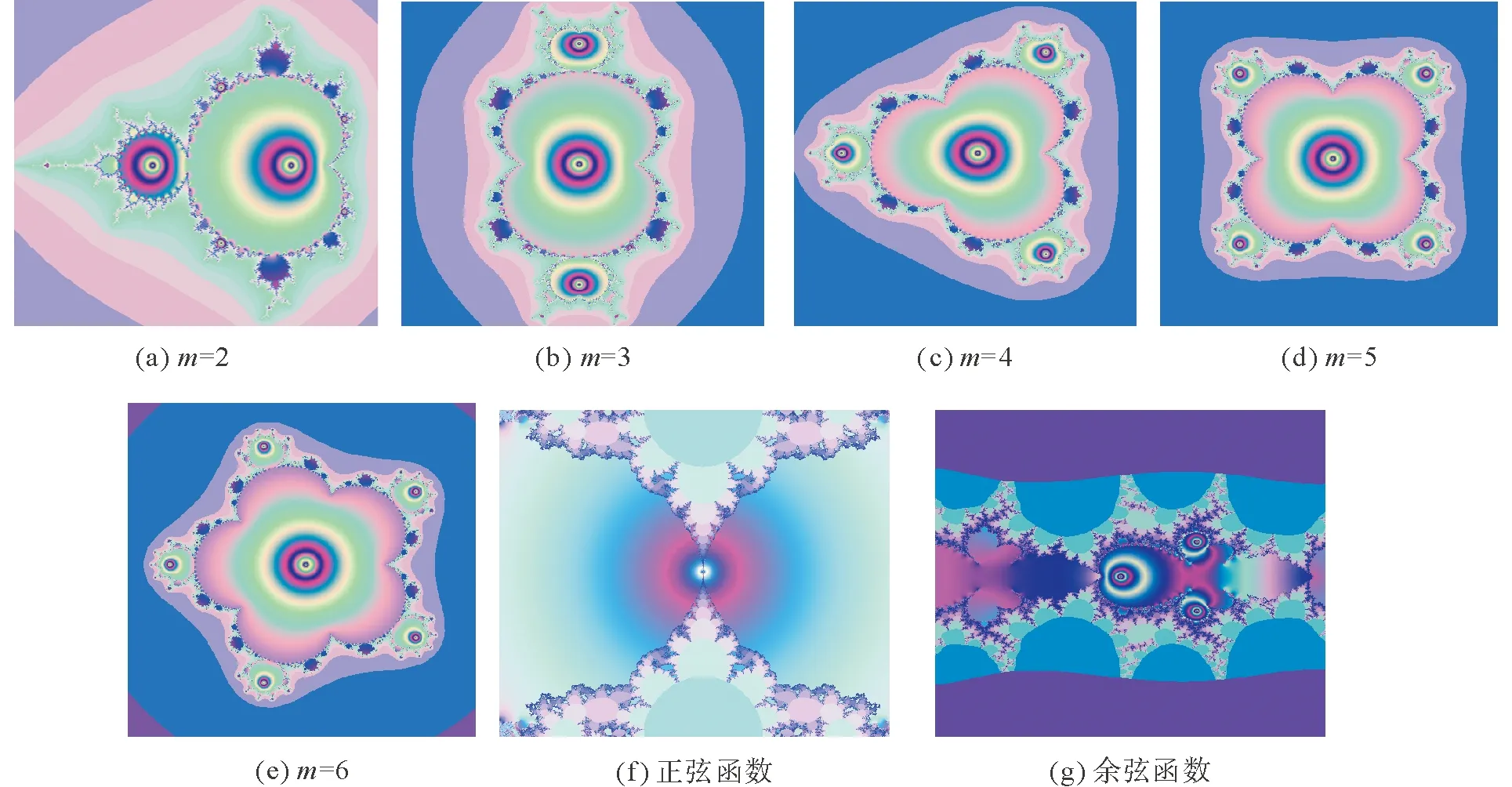
圖1 M集變化分形圖Fig.1 Changing fractal patterns of M set

令函數Z=Zm+C中冪指數m分別取值3,4,5,6時，生成的分形圖也會隨之變化，對函數進行復數運算得到如下展開式：

m=3Z= (x+iy)3=(x3-3xy2)+

(3x2y-y3)i

(2)

m=4Z= (x+iy)4=(x4-6x2y2+y4)+

(4x3y-4xy3)i

(3)

m=5Z= (x+iy)5=(x5-10x3y2+5xy4)+

(5x4y-10x2y3+y5)i

(4)

m=6Z= (x+iy)6=(x6-15x4y2+5x2y4-y6)+

(6x5y-20x3y3+6xy5)i

(5)

由此可以通過虛、實部分離，將其改寫成計算機語言，進行函數替換。程序運行結果如圖1(b)—(e)所示，分別為m取值3,4,5,6時的分形圖。

M集位于復平面上，當函數形式為三角函數，則將迭代式Z→Zm+C中Zm替換成sinz，令Z=sinz+C，由歐拉公式[9]進行展開運算得到：

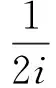
(6)

對式(6)進行虛、實部分離，轉化成計算機語言：

x′=0.5×sin(x)×(exp(-y)+exp(y))+p

(7)

y′=-0.5×cos(x)×(exp(-y)-exp(y))+q

(8)

通過編程軟件運行，結果如圖1(f)所示。同理可知余弦展開式[9]為：

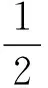
(9)

得到余弦函數分形圖如圖1(g)所示。

1.2.2 J集迭代函數的變化及變化圖形的生成

J集的基本迭代形式與M集相同，但在Z、C取值上有所不同，在J集中，C作為某一固定值，Z作為變化點進行反復迭代，可在復平面上得到J集的圖形[10-11]。J集位于復平面中，冪指數m分別取值2,3,4,5,6時會生成不同的分形圖，運行結果如圖2(a)—(e)所示。

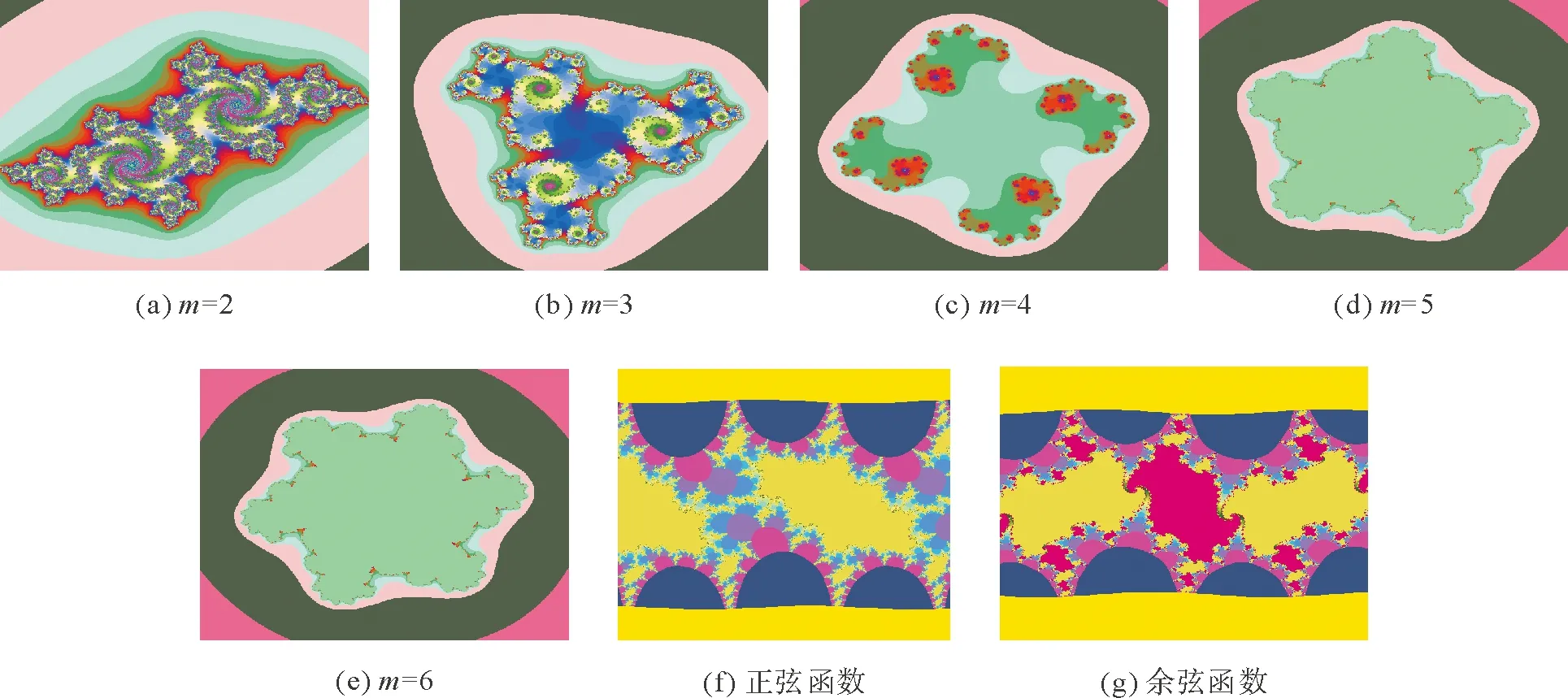
圖2 J集變化分形圖Fig.2 Changing fractal patterns of J set

J集位于復平面上，將迭代式Z→Zm+C中Zm替換成sinz、cosz，則令Z=sinz+C，變化為三角函數形式。由歐拉公式展開，并轉化成計算機語言，再通過程序設計，運行得到三角函數J集圖案，如圖2(f)(g)所示。

2 分形紋樣設計

分形圖具有一個很大的特征——自相似性，是指組成局部與整體以某種方式相似。這里提到的相似并不局限于嚴格的相似，它是大量統計顯現出的不嚴格的相似，而且無論放大多少倍，始終能看到內部有與外部輪廓相似的結構，這說明分形圖具有極精細結構[12]。基于分形圖的精細結構，分形圖在數碼紡織上具有更高的實用價值。另外，可以對分形圖進行二次處理，得到連續紋樣并應用于數碼噴墨印花技術。

紡織圖案的結構形式主要包括單獨紋樣、適合紋樣、連續紋樣等。單獨紋樣是從分形圖中直接選用整體或選取部分進行紋樣設計，單獨紋樣在外觀上并沒有具體的限制，但紋樣的構成形式應主次分明，次要部分起填充、烘托作用，突出主要部分[13]。適合紋樣是指將整體形態限定在一定形狀的范圍內，呈現出某種特定的外觀形態，其主要包括中心式、格律體、角隅式等[14]。紋樣設計如圖3所示，其中圖3(a)(b)是選取圖1(a)作為紋樣素材，圍繞中心點旋轉，形成中心對稱圖形；圖3(c)則選用圖1(f)作為紋樣素材，摳圖、復制，使兩者成90°拼接，形成角隅式紋樣。適合紋樣結構規則，外形美觀。連續紋樣是通過多次復制、往復連接，組成排列有序的圖案，生活中大家看到的圖案大部分是連續紋樣，主要分為二方連續和四方連續兩種。紋樣圖案如圖4所示，其中圖4(a)選取圖1(c)(e)作為紋樣素材，進行二方連續排列；圖4(b)以圖2(b)(c)作為基礎紋樣素材，通過改變顏色，進行變形組合，有花朵層疊感，形成四方連續紋樣。

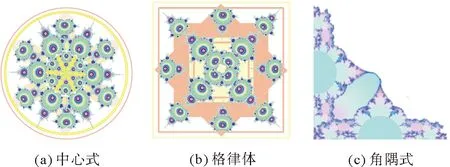
圖3 適合紋樣Fig.3 Suitable patterns

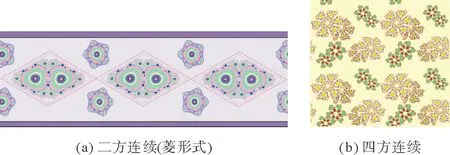
圖4 連續紋樣Fig.4 Continuous patterns

分形圖在結構、色彩上都具有獨特的風格，一些具有圓潤的曲線構圖方式，另一些具有爆破的沖擊感，可以給人在視覺上帶來新鮮感。所以分形圖可以作為新型圖案素材應用于紡織紋樣設計中，具體設計實踐步驟如下：根據設計風格和主體構思概念→選擇相應的分形圖作為素材→對選擇的分形圖進行圖像處理→根據靈感要求進行設計→通過Photoshop軟件進行實物效果演示。

2.1 設計實例1

以圖1(a)的M集分形圖作為素材紋樣，以不同的中心點以60°旋轉并復制構成中心對稱的基礎紋樣A、B，如圖5(a)所示。參照圖5(b)所示，其中紋樣A以5枚3飛緞紋組織排列，紋樣B自然穿插其中，按排列圖進行排版構成四方連續紋樣的基礎紋樣，如圖5(c)所示。拼貼成四方連續紋樣，給人活潑自然、清新明快之感。

2.2 設計實例2

以圖2(a)的J集分形圖作為素材紋樣，對素材紋樣進行摳圖、調色及變形處理，使其構成花朵的形態，基礎紋樣如圖6(a)所示。參照圖6(b)所示排列圖進行排列設計，通過選擇不同的底紋形態，產生不同的效果。

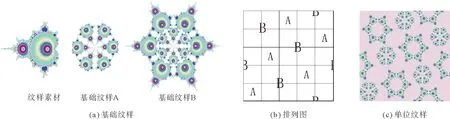
圖5 M集分形圖紋樣設計Fig.5 Pattern design of M set fractal graph

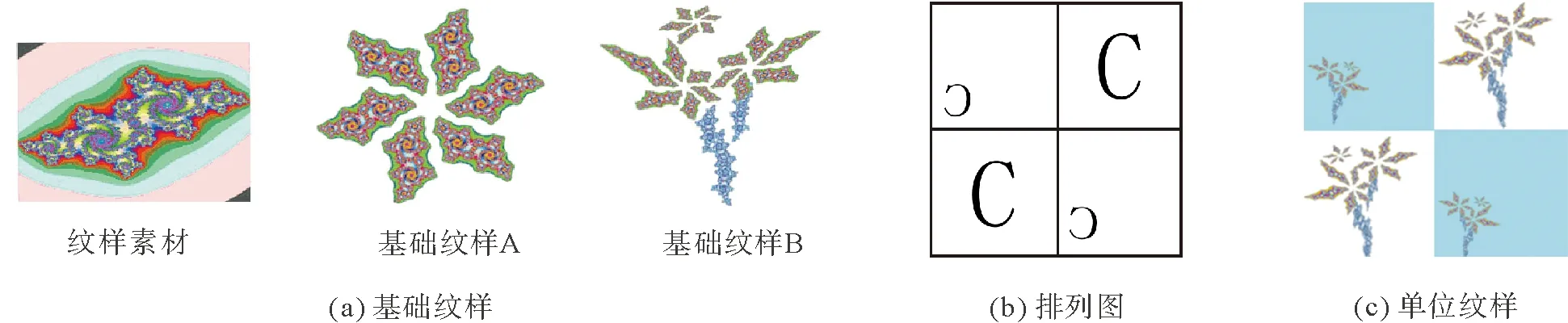
圖6 J集分形圖紋樣設計Fig.6 Pattern design of J set fractal graph

3 分形紋樣在紡織品上的應用實踐

3.1 分形紋樣效果模擬

根據上述設計實例中的紋樣設計，利用圖像處理軟件Photoshop進行效果模擬。將圖5(c)紋樣及改變底紋顏色獲得的紋樣分別應用于服裝、家紡產品上，效果如圖7所示。將圖6(c)紋樣及改變底紋樣式獲得的紋樣分別應用于服裝、家紡產品上，效果如圖8所示。由于分形圖的顯著特點是具有精細結構，原則上無論放大多少倍仍能找到與整體相似的結構。這一特點說明分形圖更適用于印染在經緯紗線較細的織物上，如絲綢、高支面料等。

圖7 模擬效果(設計實例1)Fig.7 Simulation effect (design example 1)

圖8 模擬效果(設計實例1)Fig.8 Simulation effect (design example 2)

3.2 噴墨印花實踐

選用M集分形圖作為素材紋樣，以圖5(a)中紋樣構成方法獲得基礎紋樣，對基礎紋樣進行組合排列，底紋顏色進行漸變處理，獲得如圖9所示絲巾圖案。將設計的圖像數據保存為BMP文件格式，借助導帶式直噴數碼印花機(MS-JP5)進行印花實踐，生成如圖10所示絲巾成品。

圖9 絲巾圖案Fig.9 Silk scarf pattern

圖10 絲巾成品Fig.10 Product show of silk scarf

另外，借助數碼印花機，實現分形紋樣在絲綢面料上的印花實踐，得到如圖11所示印花織物成品。

圖11 印花織物照片Fig.11 Picture of printed fabric

4 結 語

1)根據復平面上分形圖的生成方法，改變程序代碼，從而改變分形圖。分別在高次冪函數和三角函數兩種函數條件下生成變化分形圖，與基礎分形圖相比生成的分形圖色彩更加豐富、層次十分突出、結構變化復雜，具有較明顯的對稱效果，極大程度豐富了圖案設計素材庫。

2)根據紡織品主題風格與應用領域要求，對分形圖像進行選擇和處理，借助Photoshop圖像處理軟件，通過旋轉、復制、變形等基礎操作設計得到符合要求的紋樣。通過改變底紋樣式和配色改變整體紋樣風格，充分體現了分形紋樣設計的多樣性、易改變性及融合性。

3)實現復平面上分形圖的設計與數碼印花技術的完美結合，另外通過編程生成的數字圖形具有極精細結構和自相似的特點，其適用于印染在組織結構緊密的絲綢制品上。整個過程為數字化模式，精度高、周期短、綠色環保，能引領印染行業的新方向。分形圖為紡織圖案設計提供了工具，為現代紡織生產模式提供了新思路，具有廣闊的應用前景。

[1]孫博文.分形算法與程序設計:Visual Basic實現[M].北京:科學出版社,2004:9-159. SUN Bowen. Fractal Algorithm and Program Design to Achieve:VB [M]. Beijing:Science Press,2004:9-159.

[2]張聿,帥沁芬,付岳瑩,等.基于廣義Julia集的印花圖案設計[J].紡織學報,2007,28(4):80-86. ZHANG Yu,SHUAI Qinfen,FU Yueying,et al. Printing pattern designing based on general Julia set[J]. Journal of Textile Research,2007,28(4):80-86.

[3]張聿,付岳瑩.基于三角函數Mandelbrot集的印花圖案設計初探[J].絲綢,2005(1):13-14. ZHANG Yu,FU Yueying. Studies on printing pattern design based on triangle function Mandelbrot set[J]. Journal of Silk,2005(1):13-14.

[4]蔡燕燕,宋曉霞.基于Julia集分形圖形在服裝圖案設計中的應用[J].上海工程技術大學學報,2011,25(2):172-174. CAI Yanyan,SONG Xiaoxia. Application of fractal graphics in clothing pattern design based on Julia set[J]. Journal of Shanghai University of Engineering Science,2011,25(2):172-174.

[5]蔡燕燕,宋曉霞.基于Mandelbrot集的分形圖形用于絲綢圖案設計[J].絲綢,2011,48(8):35-37. CAI Yanyan,SONG Xiaoxia. Application of fractal graphs in silk pattern design based on Mandelbrot set[J]. Journal of Silk,2011,48(8):35-37.

[6]楊旭紅,顏曉華.復平面上分形信息的可視化及在紡織紋樣設計中的應用[J].絲綢,2007(7):39-47. YANG Xuhong,YAN Xiaohua. Visualization of complex plane fractal information and its application in textile pattern design[J]. Journal of Silk,2007(7):39-47.

[7]張菊香.逃逸時間算法生成的Julia集在紡織圖案設計中的應用研究[D].蘇州:蘇州大學,2009. ZHANG Juxiang. Julia Sets Generated by Escape Time Algorithm Is at the Application of the Textile Pattern Design[D]. Suzhou:Soochow University,2009.

[8]陳寧,朱偉勇.M-J混沌分形圖譜[M].沈陽:東北大學出版社,1998:69-79. CHEN Ning,ZHU Weiyong. M-J Chaos Fractal Images[M]. Shenyang:Northeastern University Press,1998:69-79.

[9]趙玉水.基于Mandelbrot集圖形的新型面料肌理設計方法[D].杭州:浙江理工大學,2010:20-21. ZHAO Yushui. Texture Design of Fabric Based on Mandelbrot Graphics[D]. Hangzhou:Zhejiang Sci-Tech University,2010:20-21.

[10]張聿,張棟高,楊旭紅,等.紡織設計中Julia集可視化信息表征方法的研究[J].蘇州大學學報(工科版),2002,22(1):25-28. ZHANG Yu,ZHANG Donggao,YANG Xuhong,et al. Studies on fabric patterns designing with visual information in Julia set[J]. Journal of Soochow University (Engineering Science Edition),2002,22(1):25-28.

[11]柯福軍,張方強.分形幾何與分形花形的迭代函數系統方法[J].紡織學報,2003,24(5):43-44. KE Fujun,ZHANG Fangqiang. Fractional geometry and fractional patterns on overlapping function system[J]. Journal of Textile Research,2003,24(5):43-44.

[12]李杰.基于遺傳算法的分形藝術圖案生成方法的研究[D].濟南:山東師范大學,2009. LI Jie. Research of Fractal Artistic Graphics Generation Method Based on Genetic Algorithm[D]. Ji’nan:Shandong Normal University,2009.

[13]胡晨晨.基于分形理論的服裝面料圖案設計及應用研究[D].杭州:浙江理工大學,2016. HU Chenchen. Fabric Pattern Design and Application Research Based on the Fractal Theory[D]. Hangzhou:Zhejiang Sci-Tech University,2016.

[14]孟廣利.L-系統分形圖在紡織紋樣設計上的應用[D].蘇州:蘇州大學,2012. MENG Guangli. Application of L-system to Textile Pattern Design[D]. Suzhou:Soochow University,2012.

收稿日期:2016-12-01;修回日期:2017-06-14

基金項目:國家社科基金藝術學一般項目(16BG112)；四川省教育廳人文社科一般項目(16SB0056)

Generationoffractalimageoncomplexplaneanditsapplicationintextiles

WANG Shuhuan,YANG Xuhong

(National Engineering Laboratory for Modern Silk,Soochow University,Suzhou 215123,China)

This paper aims to expand the application of fractal graph in textile pattern design,explore a convenient method of textile pattern design,and provide designers with more abundant and novel design materials. Firstly,according to the generation method and programming of fractal graph on complex plane,the method of generating Mandelbrot set and Julia set on complex plane was studied with Visual Basic 6.0,with a view to realizing visualization thereof. Secondly,a series of variation fractal graphs were obtained by changing the form of iterative function,pattern design and effect simulation of the obtained fractal graphs were conducted with image processing and graphic design software,and the fractal patterns were applied in textiles with printing technology. The results show that textile pattern design based on fractal graph is more suitable for the fast,efficient and changeable textile production mode.

complex plane; fractal; program design; visualization; pattern design

10.3969/j.issn.1001-7003.2017.08.010

2016-09-30;

:2017-06-13

江蘇省高校優勢學科二期建設項目(蘇政辦發〔2014〕37號)

TS941.26

:B

:1001-7003(2017)08-0056-06 < class="emphasis_bold">引用頁碼

頁碼:081202