數字指南針的數學建模應用研究

陳大方（上海市金山區青少年活動中心，上海，200000）

數字指南針的數學建模應用研究

陳大方
（上海市金山區青少年活動中心，上海，200000）

機器人的應用離不開傳感器，傳感器應用成為青少年機器人教育中的一個重要內容。其中，電子指南針的應用非常廣泛，但是電子指南針的應用有一定難度，使得廣大青少年在使用過程中束手無策。我經過研究發現主要存在以下問題：機器人在需要轉向時的方向問題——逆時針轉動還是順時針轉動？機器人在轉動過程中的速度如何，速度快的話則在目標角度有可能由于機器人控制器來不及處理角度數據而失敗（轉過頭），速度慢的話則大大降低了機器人的運行效率。鑒于以上兩個問題，本文就通過建立數學模型，把數字指南針的應用和高中階段的數學三角函數結合起來，巧妙的解決以上兩個問題。

機器人；數字指南針；傳感器應用；三角函數

1 傳感器的種類

青少年機器人教育中常用到的傳感器有：測距傳感器、尋跡傳感器、角度傳感器、測溫傳感器、觸碰傳感器、測速傳感器等。這么多傳感器按照信號分類，又可以分為模擬傳感器和數字傳感器，其中，數字傳感器又可細分為字節型數字傳感器和開關型數字傳感器。模擬傳感器應用時只需用模擬數字轉換器（Analogto-digital converter）把模擬電壓轉換成數字電壓即可，開關型數字傳感器應用簡單、編程方便，但是字節型數字傳感器應用起來就有一定的難度了。因為這類傳感器輸出的數據是一個或多個字節的二進制數，通常用到IIC、USART或SPI接口和單片機連接，運行時數據流或單向或雙向，處理時有一定的難度，但是單片機得到的數據精確，便于處理。比如，一個量程為5000mm的超聲波測距傳感器是把所測的距離以數字形式通過IIC接口直接輸出，那么“0-5000”就需要16個bit，即2個byte，這兩個byte的數據合成一個16bit的數據，來表示超聲波傳感器的測試結果。這樣聽起來很復雜，但是對使用者來說，只需接收IIC發來的數據即可，不需要自己編寫運算程序，這樣既方便了使用者，又減輕了處理器的負荷。

2 數字指南針及其問題的提出

還有一類字節型數字傳感器就是本文要講的傳感器——數字指南針。數字指南針也叫電子羅盤，是通過測量環境的磁場，從而運算得出模塊當前所指的方向角度。實際上，我們的常用的數字指南針能夠精確的檢測出當前角度（0-359°），也就是數字指南針要輸出“0-359”的數字，那么需要至少9個bit，通常用到兩個字節，我所用到的指南針是串口型（USART）的，和單片機的串口連接，每次通信都有兩個字節的數據傳輸。指南針一般有兩個按鍵：校正鍵和定位鍵。校正鍵可以使指南針適應當地的地磁環境，減小誤差；定位鍵則可以使指南針以當前角度作為零度，方便應用。

在指南針的實際應用中，我們一般用它來確定機器人的的方向。如圖1所示。

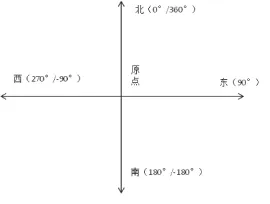
圖1

假設機器人在原點且面向北，那么可以觸發指南針的定位鍵使得當前角度為0°。在機器人運行過程中，可能會出現以下三種轉向任務：向西、向東和向南。這三個轉向任務看似簡單，但是在現場應用中會出現以下兩個問題，就以轉到向東為例說明。第一，機器人轉向的方向問題。如果程序里規定機器人永遠向左轉動，那么機器人要轉到向南（90°）的話就要轉270°而不是90°，這大大影響機器人的效率。第二、機器人轉向速度和單片機處理角度數據的矛盾。如果機器人速度稍快的話，即使指南針檢測到了90°，但是由于機器人轉向速度很快，單片機不一定就能接收到90°，導致機器人轉過頭；速度稍慢的話可能耗時太多，也影響機器人的效率。

通過以上分析，我便提出了應用中常常遇到的兩個問題：（1）轉向問題：機器人在轉向時，能否根據當前方向和目標方向自動判斷轉彎方向，使得轉彎角度最小；（2）速度問題：機器人在轉彎時既要保證速度又要準確的判斷當前角度。

3 機器人轉向問題的研究

下面我們先來研究第一個問題：機器人的轉向問題。方便起見，我假設機器人的當前角度為α，機器人要轉向的目標角度為β，令γ=（α-β）。其中，α∈[-180，0]∪[0,180]，β∈[-180，0]∪[0,180]，γ∈[-180，0]∪[0,180]。機器人在轉向時，最理想的動作是當γ∈[-180，0]時，機器人順時針轉；當γ∈[0,180]時，機器人逆時針轉。這樣轉動，不管是往哪個方向轉動，機器人都的轉動都不超過180°就會到達目標角度。也就是說，如果把γ作為自變量，γ的函數F（γ），定義域是[-180，0]∪[0,180]，且定義域關于Y軸對稱。經過研究，函數F（γ）在定義域[-180，0]和 [0,180]上的函數值要互為相反數，我們才能正確判斷機器人往哪個方向轉動。通過定義域和函數值的觀察，我發現該函數F（γ）必須為一個奇函數。在常用的三角函數中研究，發現很難找到滿足要求的函數。經過分析對比，把函數F（γ）變換成F（η），η= 0.5γ，那么函數F（η）的定義域就變成[-90，0]∪[0，90]。很容易，就找到了滿足要求的函數——正切函數F（η）=tanη。如圖2所示：

圖2

為此，我們可以輕松的寫出程序，當F（η）＜0時機器人順時針轉動，當F（η）＞0時機器人逆時針轉動。

if(tan(((double) α-(double) β)*3.14/360)＜0)

{

motor(a,-a);//順時針轉動

}

if(tan(((double) α-(double) β)*3.14/360)＞=0)

在校園生活中，班主任是學生成長的主要精神關懷者，是引導學生職業核心技能和職業核心素養全面發展的人生導師。班主任對學生的家庭背景了解，對學生行為舉止的了解，遠勝于任課老師。任課教師負責上好每堂課，布置作業，跟蹤學生的學習效果，并將作業完成情況及時反映給班主任。而班主任從旁協助，從生活上了解學生在學習過程中遇到的困難，及時給予排解。同時，在班級里營造“積極向上，你追我趕，爭當優秀”的學習氛圍，充分利用課余時間加強理論知識點的學習與鞏固，提高學生學習的興趣，調動學生學習的動力，轉變學生學習態度，化被動為主動。任課教師與班主任結對子，多方面關懷學生的成長。

{

motor(-a,a); //逆時針轉動

};

其中，motor(a,a)為馬達的子程序。(a,a)中第一個a是左邊馬達的速度值，第二個a是右邊馬達的速度值。a＞0時向前進，a＜0時向后退，a=0時向停止。a∈（-1000,1000），數據越大速度越快。

4 機器人速度問題的研究

解決了轉向的問題，我們再來研究第二個問題：機器人的速度問題。上面我已經假設機器人的當前角度為α，機器人要轉向的目標角度為β，令γ=（α-β）。根據第一個問題的結論，我們得出：α∈[-180，0]∪[0,180]，β∈[-180，0]∪[0,180]，γ∈[-180，0]∪[0,180]。機器人在轉向時，最理想的速度是機器人一開始轉彎速度很快（可以是一個常量），當到達到目標角度越小，轉彎速度應該越小，直至為零。同樣的，如果把γ作為自變量，γ的函數G（γ）定義域是[-180，0]∪[0,180]，定義域關于y軸對稱。機器人在逆時針轉和順時針轉的時候完全對稱，所以要求函數G（γ）在定義域[-180，0]和 [0,180]上的函數值也要相等。通過定義域和函數值的研究，我發現該函數必須為一個偶函數。在常用的三角函數中深入研究，我找到了滿足要求的函數——余弦函數G（γ）=cosγ。如圖3所示。

圖3

當-180＜γ=（α-β）＜-45時，即-π＜γ=（α-β機器人以恒定速度a轉向；

當45＜γ=（α-β）＜180時，即-＜γ=（α-β）＜π時，機器人以恒定速度a轉向；

if(cos(((double)de-(double)degree)*3.14/180)＜0.71)

{

a=360;

}

if(cos(((double)de-(double)degree)*3.14/180)＞=0.71)

{

a=270/cos(((double)de-(double)

degree)*3.14/180);

};

其中，a的數值就是motor（a，a）中的參數。

5 結語

至此，我利用數學建模的思想，把數字指南針和高中階段三角函數結合，解決了文章一開始提出的兩個問題。經過實踐證明，以上兩個方法科學可行，并有非常好的效果。

[1]馬潮. 《AVR單片機嵌入式系統原理與應用實踐》.

[2]張茂青. 《AVR單片機高級語言BASCOM程序設計與應用》 .

[3]2009年度. 玩轉單片機[J].《無線電》.

[4]2008版.《微積分》.上海交通大學數系微積分課程組

Research on mathematical modeling of digital compass

Chen Defang
(Jinshan District Shanghai Youth Activity Center,Shanghai,200000)

The application of robot can not be separated from sensors, and the application of sensors has become an important part of the education of young robots. Among them, the application of electronic compass is very extensive, but the application of electronic compass is difficult, which makes the vast numbers of teenagers in the process of doing nothing. I have studied and found the following main problems: when does the robot need to turn, does it turn counterclockwise or clockwise? How to speed the robot in the process of rotation, speed of words in the target angle may fail due to the robot controller to handle the data is less than the angle (turned), slow it will greatly reduce the operating efficiency of the robot. In view of the above two questions, this article through the establishment mathematics model, the digital compass application and the high school stage mathematics trigonometric function unifies, ingeniously solves these two questions.

robot; digital compass; sensor application; trigonometric function