人民幣個人理財產品收益率波動性分析
【摘要】人民幣理財產品受貨幣政策、產品設計以及經濟環境等各種因素的影響。由于因素的影響具有持續性和延續性,所以理財產品收益率的變動具有時間特性。通過ARMA模型可以分析收益率的波動性的基本特征,在ARM模型存在ARCH效用的情況下,采用GARCH模型分析人民幣理財產品收益率的波動。以此得到人民幣理財產品收益率的波動描述模型和結構化分析方法。
【關鍵詞】人民幣理財產品 收益率 GARCH模型
一、引言
伴隨著經濟的發展,金融創新形式的不斷出現,銀行理財產品正成為一種越來越重要的投資項目。銀行理財業務是商業銀行協助客戶分析自身財務狀況并充當其投資顧問的相關業務,屬于商業銀行中間業務。一般的理財產品是由商業銀行與相關的金融機構自己設計并推銷的。具體的操作過程是將所集合的資金依據產品合同投資到金融市場。在獲得收益后,再結合合約把所得分紅。
目前,銀行理財產品可以按照時間和是否保本以及收益率的固定與否劃分為多種不同的類型。因此,不同的理財產品由于屬性的不一致,導致理財產品的風險及收益各有不同。其中理財產品收益率是銀行和投資方最為關注的指標,一方面收益率是銀行設計理財產品最為重要的考慮因素,同時,收益率也是影響投資方選擇理財產品的最重要的決策指標。但是銀行理財產品的收益率并不僅受市場供求關系的影響決定,收益率的變化還受各種宏微觀環境的影響。
二、影響理財產品收益率的因素分析
貨幣政策、個人理財產品自身的設計以及國內社會環境和經濟環境的幾個方面分析其如何影響個人理財產品收益率。
(一)貨幣政策
貨幣政策指的是央行利用各種各樣的貨幣工具對利率和貨幣供給量予以調節,從而達到既定經濟目標的方針和措施的總和。貨幣政策主要分為擴張性貨幣政策和緊縮性貨幣政策,不同的貨幣政策下由于貨幣的供應量和利率的不同從而會對理財產品收益率產生影響。
一般而言,貨幣供應量增加時,商業銀行為會提高理財產品的收益率,實現幫助投資者增值保值的目的來吸引投資,而貨幣供應量減小時則為相反,商業銀行會適當降低理財產品收益率。利率的波動直接引起對應金融資產價格的波動,從而間接對掛鉤金融資產的各類理財產品收益率產生影響。利率上升時,資金面就會緊張,相應的商業銀行就會上調發行產品的收益率,奪取資金;利率下降時,資金流動足,商業銀行從資金成本的角度考慮亦不愿用高收益率產品來取得資金,因所以理財產品的收益率相對變低。
(二)產品設計
理財產品在設計的過程中,不同產品對理財產品的購買時限和權利等內容有不同的規定,并會影響雙方的收益分配,最終通過理財產品收益率的方式體現出來。其中最影響較大的時是委托期限,收益獲取方式和提前終止權。
委托期限的長短會對個人理財產品的市場風險以及資金的時間價值產生影響,從而對其收益率產生影響。一般情況下個人理財產品的委托期限與其收益率呈正相關的變動,委托期限越長,理財產品的收益率就相對較高。委托期限越短,其收益率也會相對減小。理財產品的收益獲取方式主要涉及是否保本以及收益是否固定。一般來說非保本類型的產品收益率比保本型產品的收益率高,浮動收益類型的產品收益率要比固定收益率的產品高。提前終止權使權利方擁有隨時終止產品購買持續的權利,不利于資金的管理和使用,所以,設計有客戶可提前終止權的理財產品收益率會相對減小。而銀行擁有提前終止權時,理財產品收益率會更高。
(三)經濟環境
經濟形勢整體良好的時候,包括理財產品在內的整個金融市場往往呈現出繁榮的狀態,在這種環境中的企業經營能力普遍較好,承擔風險的能力較強,信用風險較低,銀行就會調高理財產品的收益率。當外部經濟形勢整體表現不強時,金融市場也會低迷,承擔風險的能力很低,信用風險上升,銀行就會降低理財產品的收益率。
三、人民幣個人理財產品收益率ARMA模型構建
考慮到貨幣政策,經濟環境以及理財產品的設計具有一定的慣性和延續性,所以理財產品收益率的變化可以采用時間序列的方法進行模擬和分析。ARMA模型是研究時間序列的重要方法,由AR模型與MA模型“混合”構成。可以在通過檢驗的情況下用于長期追蹤理財產品收益率。
為方便研究,同時更好地與當前理財產品的情況一致,研究選取了中國銀行2016年下半年發布的中銀智薈理財計劃產品,樣本數共184個。分析思路是先進行收益率描述性分析,之后利用ARMA-GRACH模型進行波動測度,最后計算該理財產品的風險價值VaR并證明模型分析在金融領域的可行性。實證分析過程使用的軟件主要是EVIEWS和EXCEL。
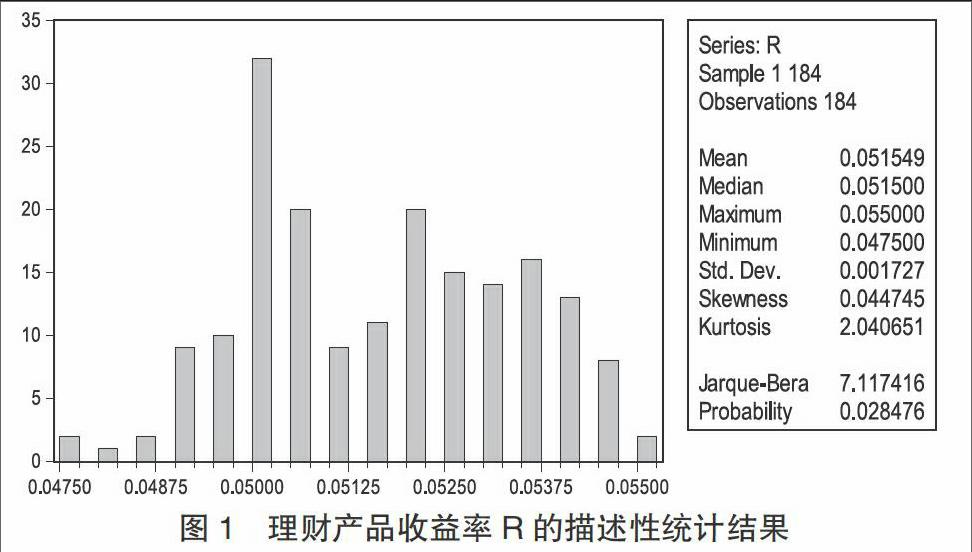
利用EVIEWS軟件,對樣本期內的理財產品收益率序列R進行描述性統計,其結果如下所示。
可以看出,2016年下半年內產品的收益率呈現出明顯的波動。理財產品樣本期內,該理財產品收益率的均值為0.051549,說明該理財產品的平均收益率為5.1549%;另外,偏度值為0.044745,大于正態分布的標準偏度值0,峰度值為2.040651,小于正態分布的標準峰度值3,因此,理財產品收益率R時間序列具體尖峰厚尾的特點。
對于收益率時間序列,可能會存在著一定的自相關,當期水平會受到前期水平的影響,故利用EVIEWS軟件計算理財產品收益率R的自相關和偏自相關數據,結果顯示序列R在1階、5階、6階、10階時的自相關函數值超過了95%的置信區間,在1階、5階、6階、10階時的偏自相關函數值超過了95%的置信區間,故應該拒絕R序列自相關函數值和偏自相關函數值為0的假設,這說明理財產品收益率R存在顯著的自相關性,需要建立自相關模型進行分析。根據ARMA模型回歸的AIC值和SC值結果可知,無論AIC值還是SC值,都是ARMA(5,6)模型的值最小,因此,理財產品收益率R的自回歸模型為ARMA(5,6),其具體公式為:
其中,εt為模型估計的隨機擾動項。
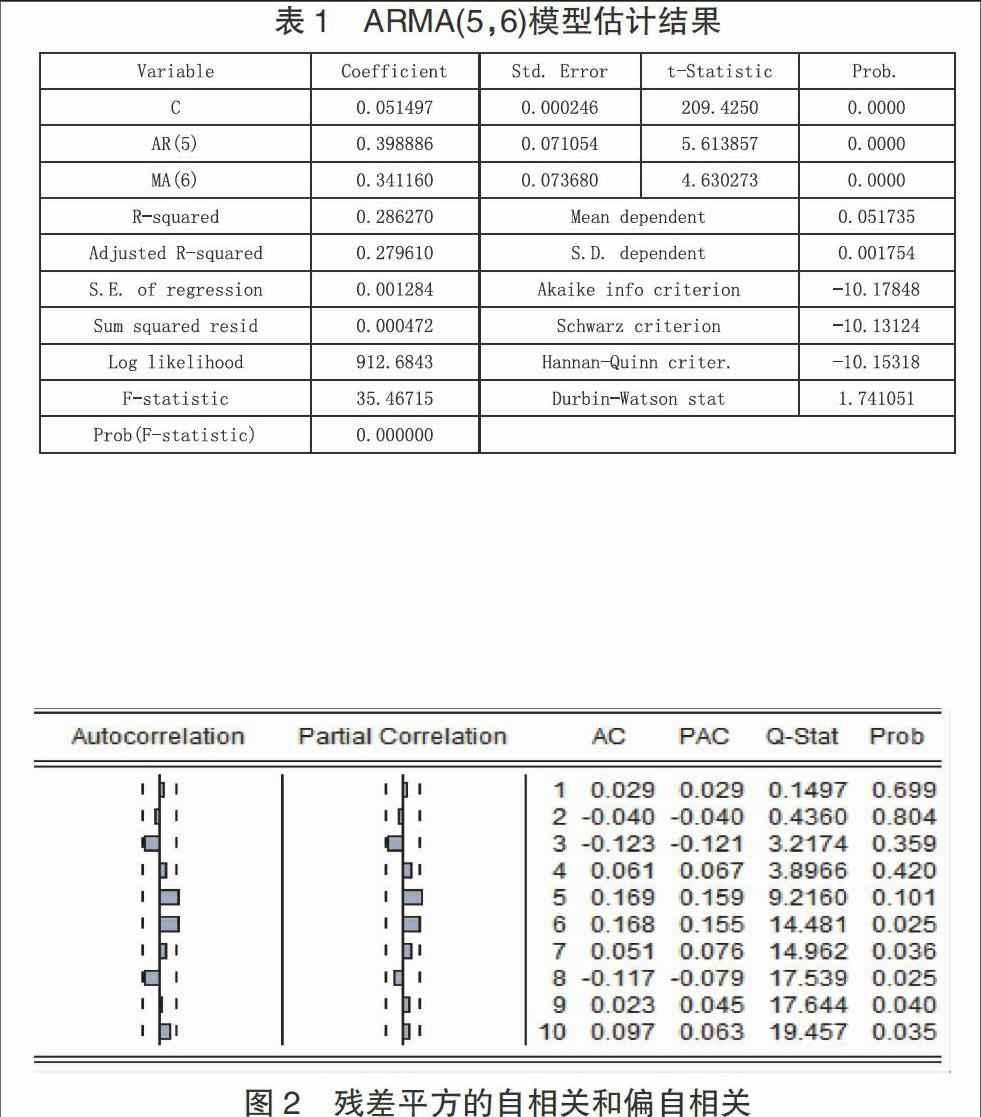
同時,得到的ARMA(5,6)模型估計結果如下表所示。
由以上表中的估計結果可以看出,AR(5)和MA(6)估計系數顯著性檢驗的P值都為0.0000,因此,估計系數都是顯著的,再次表明理財產品收益率R確實存在相關性。進一步檢驗模型是否有ARCH效應情況存在,首先得到的ARMA(5,6)模型殘差平方的自相關和偏自相關圖如下。
上圖結果顯示,自相關和偏自相關函數值在5階和6階時都超過了95%的置信區間,這說明殘差平方序列存在顯著的自相關性,故存在異方差現象。進一步采用ARCH-LM法進行檢驗,兩個統計量相對應的Prob.值都是小于0.05的,故應該拒絕不存在ARCH效應的原假設,因此,所建立的ARMA(5,6)模型確實存在ARCH效應,適合采用GARCH模型來進行分析。
四、收益率波動性特征分析
由以上的分析可知,理財產品收益率R存在著一定的ARCH效應,需要進一步建立GARCH模型來分析。在保證能夠消除ARCH效應的前提下,盡量選擇比較簡約的GARCH模型因此,構建最終采用理財產品收益率波動性分析模型為:
ARMA(5,6)-GARCH(1,1)
其具體形式如下所示:
均值方程為:■
條件方差方程為:■
采用EVIEWS軟件,對以上建立的ARMA(5,6)-GARCH(1,1)模型進行分析,殘差平方序列的自相關函數值和偏自相關函數值在各階都沒有顯著超過95%的置信區間,這說明殘差平方序列不存在顯著的自相關性,即不存在異方差現象。進一步采用ARCH-LM檢驗法驗證ARCH效應檢驗的兩個統計量P值都大于0.05,故在5%顯著水平下應該接受模型不存在ARCH效應的假設,因此,模型已經不存在ARCH效應。由此得到的ARMA(5,6)-GARCH(1,1)模型估計結果為:
均值方程為:■
條件方差方程為:■
綜合以上估計結果看出,條件方差方程中,ε■■系數反映了外部沖擊對匯率收益率波動情況的影響,其估計系數為0.046085,該系數顯著性檢驗的P值為0.2926,大于0.05,故不顯著,這說明理財產品收益率波動性受到外部沖擊的影響不明顯;ε■■的系數反映了系統的長期記憶性,其估計系數為0.912441,該系數顯著性檢驗的P值為0.0000,小于0.05,故該系數顯著,說明理財產品收益率波動性受到前期波動的顯著影響;同時,ε■■和σ■■兩個估計系數相加的和為0.958526,小于1,說明所建立的模型是穩定的。
五、結果分析
通過以上對理財產品收益率波動性的分析,可以得出如下基本結論:
一是理財產品收益率時間序列存在尖峰厚尾特征,平穩性檢驗結果顯示其是平穩的,但自相關和偏自相關顯示存在自相關性,故建立自回歸模型進行分析,通過比較選擇,最終確定的模型為ARMA(5,6),自相關性得到了消除。
二是ARCH-LM檢驗法對ARMA模型檢驗發現,模型存在著顯著的ARCH效應,故適合采用GARCH模型進行分析,最終建立的理財產品收益率波動性模型為ARMA(5,6)-GARCH(1,1)模型,該模型能夠較好地對理財產品收益率波動性進行分析。
三是在ARMA(5,6)-GARCH(1,1)模型估計的基礎上,計算得到了99%置信水平下的理財產品收益率VaR值,利用失敗檢驗法進行準確性檢驗可知,各樣本的最低收益率都沒有超過其實際收益率,故可以利用GARCH模型來進行VaR測度。
四是結合模型的實證分析結果我們可以看出經濟模型工具在分析金融工具方面有著重要的作用。商業銀行在設計理財產品的過程中可以利用經濟模型工具審慎的分析其收益率的波動性。以2016年作為例子,初期與后期的理財產品收益率波動較大,因此銀行可以在年初以及年末時相應的降低理財產品的收益率來規避風險。而在中期銀行則可以上調理財產品的收益率來實現資產的增值。
參考文獻
[1]劉鐵鷹,田波平.GARCH類模型和狀態空間模型波動率預測評價[J].財經論壇,2009(16):118-120.
[2]Yiuman Tse.Price Discovery and Volatility Spillovers in the DJIA Index and Futures Markets[J].Journal of Futures Markets,1999,19(8):911~930.
[3]Duffie,D,Singleton,K..Simulsted Moments Estimation of Markov Model-sod Asset Prices[J].Econometrica,1993(61):929—952.
作者簡介:王春雨(1977-),男,漢族,山東諸城人,任職于淮海工學院,研究方向:供應鏈與金融。

