一個幾何引理與拋物型偏轉的等效線性不動點*
周國全
(武漢大學物理科學與技術學院 湖北 武漢 430072)
一個幾何引理與拋物型偏轉的等效線性不動點*
周國全
(武漢大學物理科學與技術學院 湖北 武漢 430072)
電子在勻強電場中的電偏轉與具有磁矩的原子在非均勻磁場中的運動路徑的磁偏轉實驗——史特恩-蓋拉赫(Stern-Gerlach)實驗,是兩個典型的拋物型偏轉實驗.本文論述拋物型偏轉的等效不動點的存在性及其意義,并推導其統一的偏轉公式.
電偏轉 磁偏轉 線性不動點 史特恩-蓋拉赫實驗 偏轉公式
普通物理中的電偏轉實驗與量子、原子物理中的史特恩-蓋拉赫(Stern-Gerlach)實驗, 是物理學不同應用領域的兩個性質迥異的實驗[1~4].前者是實現示波器電子掃描的理論基礎[1~2], 后者直接驗證了原子(分子)的磁矩的空間量子化特性[3~7],從而也驗證了原子(分子)角動量與其內部電子軌道取向的量子化[3~7]. 然而,撇開具體的物理背景不論, 勻強電場中電子束的偏轉與非均勻磁場中原子路徑的偏轉卻具有相似的幾何規律. 它們都由場內的一段拋物線偏轉外加一段切向的直線運動所構成. 本文經過對這兩個實驗進行具體的分析和類比描述, 尤其闡述了拋物型偏轉的等效線性不動點的存在性, 歸納提煉出特有而共同的幾何因子, 總結出統一的偏轉公式.
1 一個幾何引理
為方便展開有關拋物型偏轉的線性不動點的討論, 先證明如下數學命題以作后文引理.


(1)
或 2kx0x-y-y0=0
(1′)
(2)

(3)

圖1 拋物線切線族的不動點
2 拋物型電偏轉的等效不動點與偏轉公式

(4)
其中入射初速率v滿足
(5)
由式(4)、(5)可得該電子的拋物線運動方程為
(6)
相應的參數k為
(7)

圖2 電偏轉的等效線性不動點


(8)
或
(9)
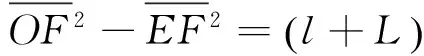
(10)
以上偏轉公式(8)、(9)在忽略場的邊緣效應的情況下嚴格成立, 不必強調“偏轉板到熒光屏的距離遠大于偏轉板長度”而置該公式于“近似”的地位. 此外, 為了實現電偏轉還必須滿足出射約束條件


(11)
3 拋物型磁偏轉的等效線性不動點——史特恩-蓋拉赫實驗
如圖3所示,史特恩-蓋拉赫實驗是在非均勻橫向磁場中發生原子路徑的橫向偏轉, 它是拋物型偏轉的又一典型實例, 歷史上被用來證實原子軌道取向及角動量、磁矩的量子化規律.

圖3 史特恩-蓋拉赫實驗的等效線性不動點

Fy=(μB)=μ
(12)
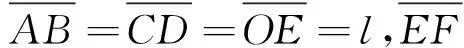
(13)
拋物線運動方程為
(14)
其拋物線參數k為
(15)
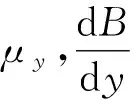
(16)
注意上式也具有空間幾何因子
為保證原子在G點出射, G點的偏轉距離DGy必須滿足約束條件
即

(17)
4 統一的偏轉公式
綜上所述, 無論是電子束在勻強電場的電偏轉實驗, 還是原子束在非均勻橫向磁場中的史特恩-蓋拉赫實驗, 粒子在場域內做一段拋物線運動,在場域外做直線運動,其出射線的反向延長線必通過其初始入射方向的延長線在場域部分的中點, 就如同是從場域中點發出的射線一樣, 我們稱之為拋物型偏轉的等效線性不動點.它的存在使問題的處理變得相當簡便.另一方面, 由于兩類拋物型偏轉具有相同的空間幾何因子,因此它們的偏轉公式(9)、(16)具有相似而統一的形式
(18)

(19)

(1)忽略場的邊緣效應;

式(11)與式(17),亦即
(20)
1 林抒, 龔鎮雄. 普通物理實驗.北京:人民教育出版社,1981.328~332
2 周殿清.普通物理實驗教程.武漢:武漢大學出版社,2005.98~104
3 褚圣麟.原子物理學.北京:高等教育出版社,1979.42~61
4 H·哈肯,H·C·沃爾夫,著.原子與量子物理學.劉歧元,譯.北京:科學出版社,1993.241~243
5 郭奕玲.斯特恩-蓋拉赫實驗, 大學物理, 1984,3(10): 27~30
6 寧長春,汪亞平,胡海冰,等.斯特恩-蓋拉赫實驗歷史概述.大學物理, 2016,35(3):43~49
7 吳榕生.斯特恩-蓋拉赫實驗中原子受力的分析.大學物理,1986(2):5~7
8 郭大鈞.大學數學手冊.濟南:山東科學技術出版社,1985.70~73
Highlights:The existence and specific properties of the equivalent linear fixed points,for the parabolic deflection about the moving path of a point charge in a uniform electric field, and an atom with magnetic moment in a non-uniform magnetic field, were thrown light on, and a unified deflection formula was also deduced.
AGeometricLemmaandtheEquivalentLinearFixedPointofParabolicDeflection
ZhouGuoquan
(SchoolofPhysicsandTechnology,WuhanUniversity,Wuhan,Hubei430072)
parabola;electric deflection;magnetic deflection,fixed point;Stern-Gerlach experiment;deflection formula
*高等學校電動力學課程教學研究項目,項目編號:JZW-16-DD-15
周國全(1965- )男,博士,副教授,從事大學物理與理論物理教學工作, 非線性可積方程與場論研究.
2017-02-16)

