廣義切換系統的脈沖性質及其穩定性
劉玉忠, 尹玉娟
(1. 沈陽師范大學 數學與系統科學學院, 沈陽 110034; 2. 遼寧大學 數學學院, 沈陽 110036)
運籌學與控制論
廣義切換系統的脈沖性質及其穩定性
劉玉忠1, 尹玉娟2
(1. 沈陽師范大學 數學與系統科學學院, 沈陽 110034; 2. 遼寧大學 數學學院, 沈陽 110036)
廣義切換系統是一類重要的混雜動態系統,有著廣泛的實際背景。研究了廣義切換系統由于非一致的初始條件引起的狀態跳變問題,同時討論了一致初始條件和非一致初始條件下廣義切換系統解之間的關系。廣義切換系統的每個子系統具有不同的代數約束條件,這類廣義切換系統的特點是在每一個切換時刻都有脈沖影響作用于系統。將標稱切換系統的多李雅普諾夫方法應用于該類帶有脈沖作用的廣義切換系統,對每一個子系統,引入類李亞普諾夫函數(Lyapunov-like Function),基于類李亞普諾夫函數和多李亞普諾夫函數方法,得到了系統穩定的充分條件。
切換系統; 廣義切換系統; 脈沖控制; 多李雅普諾夫函數
0 引 言
系統的穩定性是切換系統研究的基本問題。近幾十年,切換系統的穩定性受到了許多學者的普遍關注[1-8]. 基于切換系統的特點,多李雅普諾夫方法在研究切換系統穩定性方面得到了廣泛地應用。
多李雅普諾夫函數方法最早在文獻[1]提出.眾所周知,如果李雅普諾夫函數在切換時刻的值是減少的,那么切換系統是穩定的。在文獻[2]中引入了類-李雅普諾夫函數,并且每個子系統的類-李雅普諾夫函數在激活的子系統左端值是減少的就能保證切換系統的穩定性。文獻[6-7]推廣了上述結果,即允許李雅普諾夫函數的值在被激活子系統適當的“增加”仍能保證系統的穩定性。文獻[8]引入了帶有松弛變量的切換李雅普諾夫函數,給出系統漸近穩定的充分條件,該條件表示成易于求解的線性矩陣不等式的形式 (LMI).
廣義系統是一類更一般化并有著廣泛應用背景的動力系統,它大量出現在許多實際的系統模型中,例如電力系統、能源系統、航天工程、化學過程、經濟系統、社會系統和生物系統等[9-10]。本文將多李雅普諾夫函數方法應用于具有脈沖作用的廣義切換系統,把各子系統的代數約束描述為脈沖作用的廣義切換系統,并給出系統穩定的充分條件。
1 預備知識
1.1 初始狀態的描述
考慮廣義系統
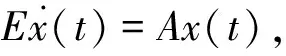
(1)
這里:x(t)∈Rn是狀態向量;E,A∈Rn×n,B∈Rn×p是常矩陣。設rank(E)=q 若系統(1)是正則的,那么存在非奇異矩陣Q、P使得 這里:A1∈Rq×q;N∈R(n-q)×(n-q);I是單位矩陣,從而系統(1)受限等價于下面的系統: (2) 由式(2)得 (3) 顯然,如果N≠0,那么只要x2(0-)≠0,任意初始狀態均會對系統產生脈沖作用。下面只考慮沒有脈沖作用的情形,即N=0。 由式(3)和式(2)可得 (4) 因此 一般地,對任意的t0>0,可得到類似的結果,即 (5) 1.2 一致初始條件和非一致初始條件 (6) 考慮如下廣義切換系統 (7) 其中:σ(t):R+→Λ={1,2,…,m}是分段常值右連續的切換信號;x(t)∈D?Rn是狀態;D是Rn空間上的子流形;Ei,Ai∈Rn×n是常矩陣。假設每個子系統(Ei,Ai)都是正則無脈沖的,rank(Ei)=r,并且存在矩陣Qi,Pi使得 (8) 考慮如下脈沖廣義系統: (9) 其中切換信號σ(t)及矩陣Pi同系統(7)。 定義2 設T是R+上嚴格增的序列,稱函數V:Rn→R+為廣義系統(E,A)的類-李亞普諾夫函數,如果滿足下列條件: 2) V是(T)上單調非增的函數。. 利用上述類-李亞普諾夫函數可以得到下面的較少保守性的穩定性條件。 定理 假設Vi是系統(Ei,Ai)的類-李亞普諾夫函數, i=1,2,…,m,是所有切換序列的集合。對任意的S∈, i∈Λ, Vi是系統(Ei,Ai)在S|i上的類-李亞普諾夫函數,那么系統(9)是穩定的。 證明 不失一般性,僅證明m=2的情形。 注2 這個結果是文獻[2]中相關結果的推廣,文獻[2]中研究的廣義切換系統在切換時刻沒有狀態跳躍,然而在實際上,系統狀態在切換時刻前后受到不同的代數約束,往往會引起狀態跳躍。 本文研究了非一致初始條件引起的脈沖系統和廣義切換系統的狀態跳躍問題,利用多李雅普諾夫函數方法對該類系統的穩定性分析,得到了系統穩定的充分條件。 [ 1 ]PELETIES P,DECARLO R A. Asymptotic stability of m-switched systems using Lyapunov-like functions[C]∥Proceedings of ACC, 1991:1679-1684. [ 2 ]BRANICKY M S. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems[J]. IEEE Trans Automat Contr, 1998,43(4):475-482. [ 3 ]LIBERZON D. Switching in systems and control[M]. Boston: Birkhauser Press, 2003. [ 4 ]LIBERZON D,Morse A S. Basic problems in stability and design of switched systems[J]. IEEE Control Systems Magazine, 1999,19(5):59-70. [ 5 ]BRANICKY M S. Stability of switched and hybrid systems[C]∥Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, Florida, 1994:3498-3503. [ 6 ]HOU L,MICHEL A N,YE H. Stability analysis of switched systems[C]∥Proceedings of 35thIEEE CDC, 1996:1208-1212. [ 7 ]PETTERSSON S,LENNARTSON B. Stability and robustness for hybrid systems[C]∥Proceedings of 35th IEEE Conference on Decision and Control, 1996:1202-1207. [ 8 ]DAAFOUZ J,RIEDINGER P,IUNG C. Stability analysis and control synthesis for switched systems: a switched lyapunov function approach[J]. IEEE Automat Control, 2002,47(11):1883-1887. [ 9 ]DAIL Y. Singular Control Systems[M]. Berlin: Spring-Verlag, 1989. [10]LEWIS F L. A survey of linear sigular systems[J]. Circuits systems signal process, 1986,5(1):3-36. [11]SINCOVEC R F,ERISMAN A M,YIP E L,et al. Analysis of descriptor systems using numerical algorithms[J]. IEEE Trans Automat Contr, 1981,26(1):139-147 Impulsiveproperty of switched singular systems and its stability LIUYuzhong,YINyujuan (1. College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China; 2. College of Mathematics, Liaoning University, Shenyang 110032, China) Switched singular system is one of the important hybrid dynamical systems. In this paper the problem of state jumps due to inconsistent initial conditions is addressed for impulsive and switched singular systems. The relationship between the solution with inconsistent initial condition and the one with consistent initial condition is discussed as well. The switched singular systems of each subsystem with different algebraic constrain conditions is modeled by switched singular systems with impulsive effects on switching instants. Multiple Lyapunov function approach for normal switched systems is extended to the impulsive and switched singular systems. For each subsystem, the Lyapunov-like function is introduced and the sufficient condition for the systems to be stable is given based on the Lyapunov-like function and Multiple Lyapunov function. switched systems; switched singular systems; impulsive control; multiple Lyapunov functions 2017-06-05。 遼寧省教育廳科學研究一般項目(L2014433)。 劉玉忠(1963-),男,遼寧新賓人,沈陽師范大學教授,博士; 通信作者: 尹玉娟(1964-),女,遼寧沈陽人,遼寧大學教授,博士。 1673-5862(2017)03-0296-04 TP13 A 10.3969/ j.issn.1673-5862.2017.03.007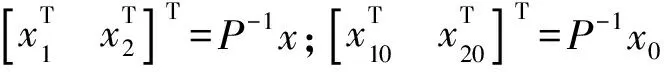
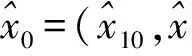
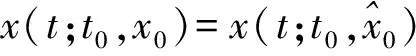
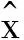
2 穩定性分析
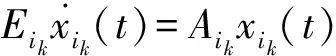
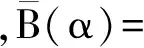
3 結 論