基于邏輯回歸的流失預警模型

郭向紅

(內蒙古移動公司 內蒙古 呼和浩特 010000)

基于邏輯回歸的流失預警模型

郭向紅

(內蒙古移動公司 內蒙古 呼和浩特 010000)

當輸入變量過多時，邏輯回歸模型訓練的時間會很長，而且更重要的是往往因為運算量過大而無法進行。因此，本文討論了利用主成分分析進行變量降維，介紹了邏輯回歸的基本理論和流失預警模型的開發過程。

邏輯回歸；流失預警模型

一、模型簡介

回歸分析在諸多行業和領域的數據分析應用中發揮著極為重要的作用，盡管如此，在運用回歸分析方法時仍不該忽略方法應用的前提假設條件。違背了某些關鍵假設，則得到的分析結論很可能是不合理的。比如，利用多元回歸分析變量之間關系或者進行預測時的一個基本要求就是：因變量均是連續型變量。然而實際應用中這種要求未必都能得到較好的滿足，如本文所討論的根據通信用戶近期的消費行為和通話行為特征，建立通信用戶的是否有流失傾向的回歸分析模型，來判斷用戶是否有潛在的流失意愿。這個模型中的因變量設為是否有可能流失，這是個純粹的二值品質型變量，顯然不滿足上面的要求。對于這類問題，我們通常采用邏輯回歸進行解決。

當輸入變量過多時，邏輯回歸模型訓練的時間會很長，而且更重要的是往往因為運算量過大而無法進行。因此，本文首先討論了利用主成分分析進行變量降維，然后介紹了邏輯回歸的基本理論和流失預警模型的開發過程。

(一)使用主成分分析進行數據預處理

在許多實際問題中，我們經常用多個變量來刻畫某一事物，但由于這些變量之間往往具有相關性，很多變量帶有重復信息，這樣就給分析問題帶來了很多不便，同時也使分析結論不具有真實性和可靠性，因此，人們希望尋找到少量幾個綜合變量來代替原來較多的變量，使這幾個綜合變量能較全面地反映原來多項變量的信息，同時相互之間不相關。主成分分析是滿足上述要求的一種處理多變量問題的方法。

1.基本思想

主成分分析就是設法將原來的p個指標重新組合成一組相互無關的新指標的過程。通常數學上的處理就是將原來的p個指標做線性組合。為了能更清晰的解釋主成分的基本思想，我們從用兩個指標來衡量n個樣本點的二維空間入手。

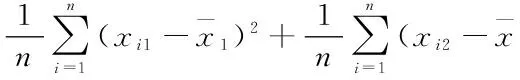
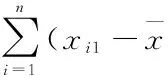
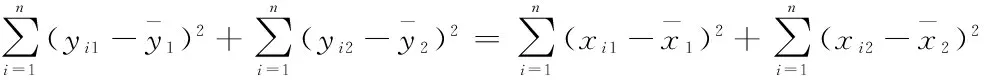
推而廣之，第一主成分y1的方差達到最大，其方差越大，表示其所包含的信息越多。如果第一主成分還不能反映原指標的全部信息，再考慮選取第二主成分y2，y2在剩余的線性組合中方差最大，并且與y1不相關，如若第一、第二主成分仍然不能反映原變量的全部信息，再考慮選取第三主成分y3，y3在剩余的線性組合中方差最大，并且與y1、y2不相關，依此可求出全部p個主成分，它們的方差是依次遞減的。在實際工作中，在不損失較多信息的情況下，通常選取前幾個主成分來進行分析，達到簡化數據結構的目的。

2.數學模型

主成分分析可以針對總體，也可以針對樣本，但在許多問題中所涉及的總體都是未知的，所以我們主要討論樣本的主成分。仍從二維空間入手，設有兩個變量的信息如圖所示，大部分的樣本點集中在橢圓范圍內：

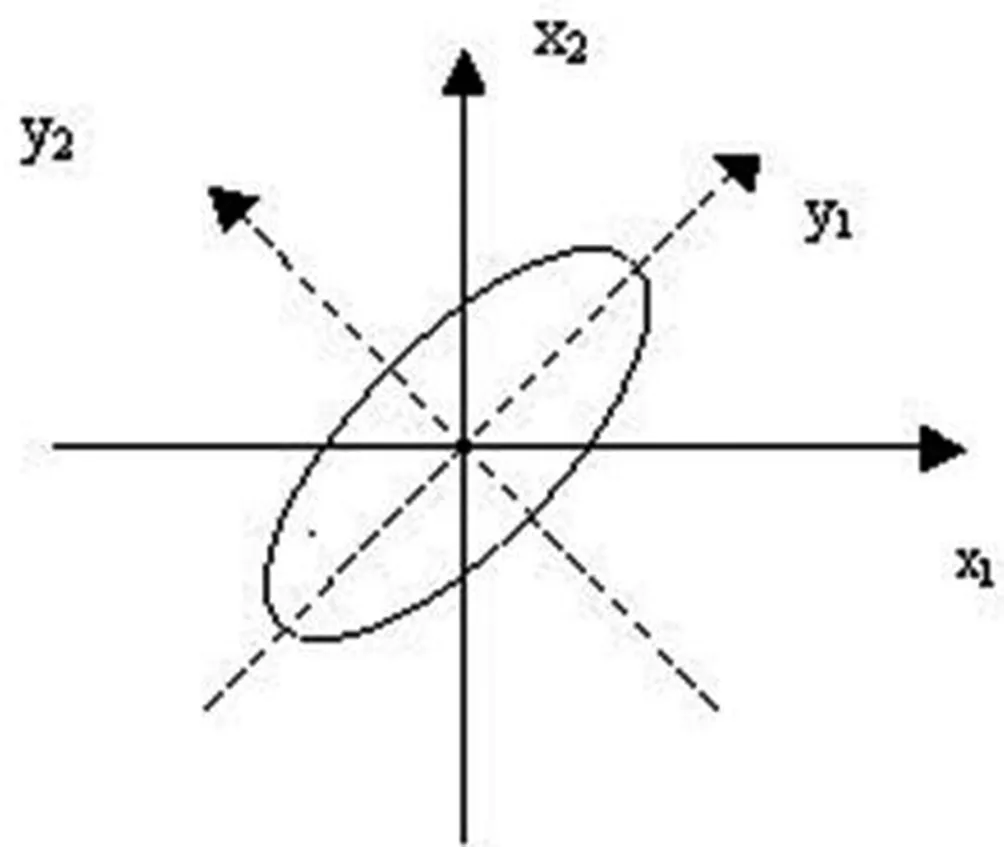
兩個變量的信息分布

如果我們取橢圓的長軸y1、短軸y2作為樣本點新的坐標軸，容易看出y1坐標變化程度大，即y1的方差最大，而y2的變化程度相對較小，即y2的方差較小。于是可以說變量(x1，x2)的信息大部分集中在新變量y1上，而小部分集中在新變量y2上。上圖中的新坐標y1，y2是x1，x2經過坐標旋轉而得到的，其旋轉公式為：

y1=cosθx1+sinθx2

y2=-sinθx1+cosθx2

系數滿足的要求是：

(cosθ)2+(sinθ)2=1;(-sinθ)2+(cosθ)2=1;cosθ(-sinθ)+sinθcosθ=0

我們可以稱y1為它們的第一主成分，y2為它們的第二主成分，坐標的正交變換為主成分變換。推廣開來，設有n個樣本點，每個樣本點都有p項變量x1,x2,…,xp，其原始數據矩陣表示為：

其中xij是第i個樣本點第j個指標的觀測值。如前所述，通過主成分變換得到的線性組合可以表示為x1,x2,…,xp的線性組合：

y1=u11x1+u12x2+……+u1pxp

y2=u21x1+u22x2+……+u2pxp

…………

yp=up1x1+up2x2+……+uppxp

3.模型求解

為了求出主成分，只需求樣本協方差矩陣S或相關系數矩陣R的特征根和特征向量就可以。設R的特征根λ1≥λ2≥…≥λp>0， 相應的單位特征向量為：(ui1ui2… uip)’，那么相應的主成分就是：yi=ui1zx1+ui2zx2+……+uipzxp。

4.實驗結果

采用TWM軟件中的主成分分析模塊，對有400多個變量字段的數據挖掘寬表進行降維操作。發現前30個主成分變量的累計方差貢獻為61.8%，提取這些變量，作為邏輯回歸模型的輸入變量。

二、邏輯回歸流失預警模型

(一)邏輯回歸模型

邏輯回歸是根據輸入字段值對記錄進行分類的一種統計技術。當被解釋變量為0/1二值變量時，稱為二項邏輯回歸。二項邏輯回歸雖然不能直接采用一般線性多元回歸模型建模，但仍然可以充分利用線性回歸模型建立的理論和思路進行建模。

1.若采用簡單線性回歸模型，即Yi=β0+βixi+εi，當Yi只取0，1兩值時，由ε～N(0,σ2)，E(ε)=0，

有E(Yi)=β0+βixi=1×P+0×(1-P)=P，即E(Yi)為xi時yi=1的概率值。因此，可以利用一般線性多元回歸模型對因變量為1的概率P進行建模，此時模型因變量的取值范圍就是0到1之間，即Py=1=β0+βixi。

2.由于概率P的取值范圍為[0,1]，而一般線性回歸模型要求因變量取值為(-∞,+∞)，因此可以對概率P做轉換處理。而一般線性模型建立關于因變量取值為1時的概率的回歸模型時，模型中自變量與概率值之間的關系是線性的。在實際應用中，這個概率與自變量之間往往是一種非線性關系。因此，對概率P的轉換處理采用非線性轉換(Logit變換)，具體如下：

(1)第一步，將P轉換成Ω，即Ω=P/(1-P)，其中Ω成為發生比，是事件發生的概率與不發生的概率的比值。可得Ω是P的單調增函數，從而保證了P與Ω增長的一致性，由此得出Ω的取值范圍為(0,+∞)。

(2)第二步，將Ω轉換成lnΩ，即lnΩ=ln(P/(1-P))，式中lnΩ稱為Logit P，經過變換后的Ω與Logit P之間的增長性一致，且Logit P取值為(-∞,+∞)。經過Logit變換后，可以利用一般線性回歸模型建立自變量與因變量之間的關系模型，即邏輯回歸模型LogitP=β0+βixi轉換為ln(P/(1-P))=β0+βixi，于是有P/(1-P)=exp(β0+βixi)，從而有：

此式即為邏輯回歸函數，它是典型的增長函數，能很好的體現概率P和自變量間的非線性關系。

(二)邏輯回歸方程中回歸系數的含義

邏輯回歸模型采用極大似然估計法對模型的參數進行估計。極大似然估計法是一種在總體分布密度函數和樣本信息的基礎上，求解模型中未知參數估計值的方法。它基于總體的分布密度函數構造一個包含未知參數的似然函數，并求解在似然函數值最大下的未知參數值。因為在形式上，邏輯回歸模型與一般線性回歸模型相同，所以可以以類似的方法理解和解釋邏輯回歸模型系數的含義。即當其他自變量保持不變時，自變量xi每增加一個單位，將引起Logit P增加(或減少)βi個單位。但是Logit P無法直接觀察且測量單位也無法確定，因此通常以邏輯回歸函數的標準差作為Logit P的測度單位。在現實應用中，大家通常更為關心的是自變量變化引起概率P變化的程度，因為它們之間的關系是非線性的。因此，人們將注意力集中在自變量給Ω帶來的變化。

當邏輯回歸模型的回歸系數確定后，將其代入Ω的函數，即Ω=exp(β0+βixi)。當其他的自變量保持不變，xi增加一個單位時，可將新的發生比設為Ω′，則有Ω′=Ωexp(βi)。由此可知，當xi增加一個單位時將引起發生比擴大exp(βi)倍，當回歸系數為負時發生比縮小。

(三)邏輯回歸方程的檢驗

1.回歸方程的顯著性校驗

邏輯回歸方程顯著性檢驗的目的是檢驗自變量全體與Logit P的線性關系是否顯著，是否可以用線性模型擬合。基本思路是：若方程中的諸多變量對Logit P的線性解釋有顯著意義，則會使得回歸方程對樣本的擬合得到顯著提高，可采用對數似然比測度擬合程度是否有了提高。其零假設為H0：各回歸系數同時為0，自變量全體與Logit P的線性關系不顯著。

2.回歸系數的顯著性校驗

邏輯回歸系數顯著性檢驗的目的是逐個檢驗模型中各自變量是否與Logit P有顯著的線性關系，以解釋Logit P是否有重要貢獻。其零假設為H0:βi=0，即某回歸系數與零無顯著性差異，相應的自變量與Logit P的線性關系不顯著。回歸系數的顯著性檢驗采用的是檢驗統計量為Wald檢驗統計量，數學定義為Wald=(βi/Sβi)2。其中βi是回歸系數，Sβi是回歸系數標準誤差，Wald檢驗統計量服從χ2(1)分布。

3.回歸方程的擬合優度校驗

在邏輯回歸分析中，擬合優度可以從兩方面考察：一方面是回歸方程能夠解釋因變量的變差的程度，如果方程可以解釋因變量較大部分的變差，則說明擬合優度高，反之說明擬合優度低；另一方面，由回歸方程計算出的預測值與實際值之間吻合的程度，即方程的總體錯判率是低還是高，如果錯判率低，說明擬合優度高，否則說明擬合優度低。擬合優度檢驗的常用指標有Cox & SnellR2統計量，Nagel ker keR2統計量，錯判矩陣，殘差分析等。

4.模型訓練過程和結果

利用得到的前30個主成分變量，采用TWM工具中的邏輯回歸模型進行訓練。然后將訓練后的模型作為評分模型，對用戶信息進行評分，從而分析出可能流失的客戶。