小球在斜面上的滾滑運動

徐文杰 于正榮

(1. 鹽城市教育科學研究院,江蘇 鹽城 224005； 2. 鹽城市伍佑中學,江蘇 鹽城 224041)

小球在斜面上的滾滑運動

徐文杰1于正榮2

(1. 鹽城市教育科學研究院,江蘇 鹽城 224005； 2. 鹽城市伍佑中學,江蘇 鹽城 224041)

本文針對一道中學階段常見的習題,研究了均質小球在斜面上釋放后的運動情況．指出滾動與滑動的差異,并給出小球做純滾動的條件,進一步說明了小球在做純滾動和又滾又滑運動時能量轉化的關系．

均質小球;斜面;純滾動;又滾又滑

1 問題的提出

下面一道常見的中學物理習題,很有深入探討的必要．

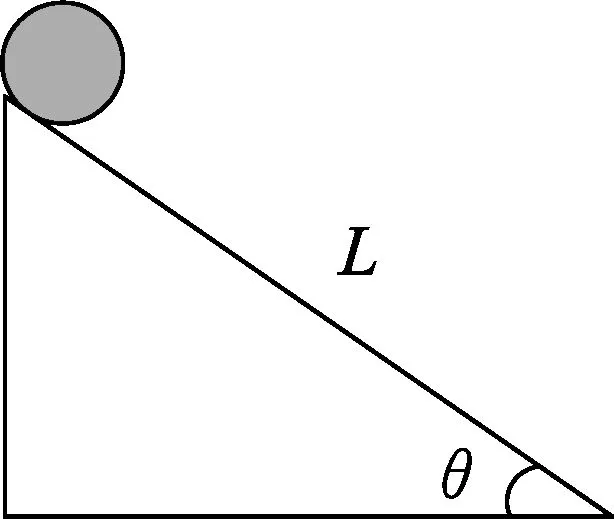
圖1

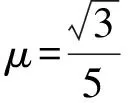
本例題粗看非常簡單,常見的解析大致如下.

常規解析:小球在運動過程中受到重力mg、斜面的支持力N和摩擦力f作用,設小球沿斜面向下運動的加速度為a．則根據牛頓第二定律有

mgsinθ-f=ma.

并且小球所受的滑動摩擦力f滿足

f=μmgcosθ.

由于小球從靜止開始沿斜面做勻加速直線運動,根據運動學公式有

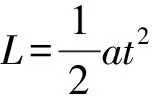
由以上3式可解得小球在斜面上運動的時間為

上述解答看似無可厚非,實際上存在重大問題．因為小球釋放后,不僅沿斜面向下平動,并且由于摩擦力的存在,小球同時還將繞質心轉動．轉動的存在會對小球的運動產生什么影響呢?另外,有人認為,小球之所以稱為“小”,其半徑應該是可以忽略的,這樣就完全可以把小球等效成方形滑塊來處理,這種看法又是否正確呢?下面筆者試圖對這個問題進行詳細研究,以期得到一個較為明確的認識,供大家在教學中參考．

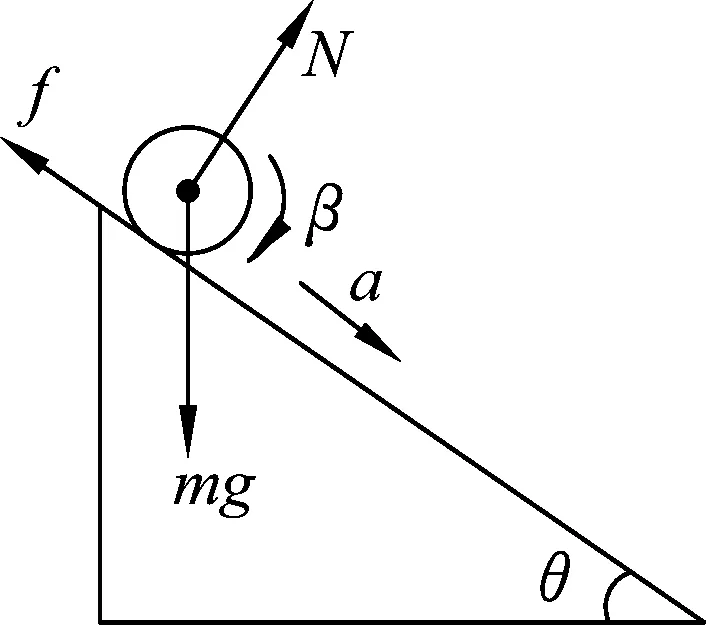
圖2

2 問題的分析

首先分析小球在斜面上運動時的受力情況,小球受到重力mg、支持力N和摩擦力f作用,如圖2所示．這里需要注意的是摩擦力的作用點與小球的質心并不重合,而是位于小球與斜面的瞬時接觸點處,正是這個原因小球才會轉動．由于小球涉及平動和轉動,因此須用剛體力學知識求解．設小球的半徑為r,小球質心沿斜面向下運動的加速度為a，同時小球繞質心轉動的角加速度為β．對小球質心的運動,根據質心運動定理有

mgsinθ-f=ma,

(1)

小球由于繞質心轉動,根據動量矩定理有

fr=Iβ,

(2)

對于質量分布均勻的實心球體,其轉動慣量I滿足

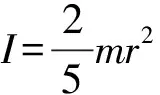
(3)

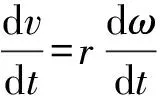
a=rβ.

(4)

根據以上4式可解得小球質心沿斜面向下運動的加速度為

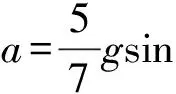
(5)

顯然,小球的質心在做勻加速直線運動,所以小球在斜面上的運動時間為

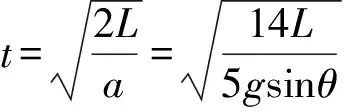
(6)

將前文例題中的數據代入(6)式,可算得小球在斜面上的運動時間t=0.748s,這與常規解析的1s時間相差較大．不過,例題中的小球能做純滾動嗎?下面繼續討論．

將(5)式代入(1)式可解得小球做純滾動時所受到的摩擦阻力為

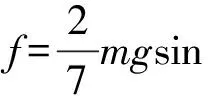
(7)

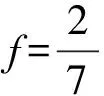
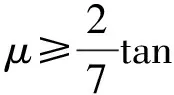
(8)

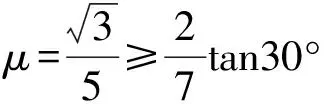
另外,由于小球與斜面之間的摩擦力是靜摩擦力,它的存在雖然導致質心的加速度小于斜面光滑的情況(a=gsinθ),但由于它的作用點的位移為0,即此靜摩擦力不做功,所以小球在做純滾動時,機械能實際上是守恒的．不過,需要強調的是,這時小球的動能包含兩部分,即質心運動的動能和小球內各點繞質心轉動的動能．研究小球從開始釋放直至斜面底端的過程,根據機械能守恒定律有

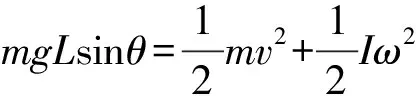
(9)

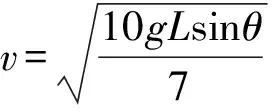
再有,由于(5)～(7)式的結果與小球的半徑無關,因此我們絕不可以說只要小球的半徑足夠小,其運動情況就與方形滑塊等同．

3 問題的拓展

由于小球相對于斜面存在滑動,此時所受摩擦力實際是滑動摩擦力,其大小滿足

f=μmgcosθ,

(10)

將(10)式代入(1)式,可解得小球質心相對于斜面的加速度為

a=g(sinθ-μcosθ).

(11)

另外,將(10)式代入(2)式,并結合(3)式可解得小球繞質心轉動的角加速度為

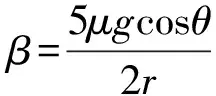
(12)

由此可得小球相對斜面滾動(即小球與斜面的接觸點繞質心轉動)的加速度大小為

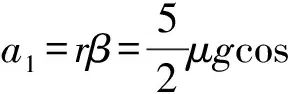
(13)

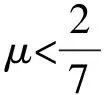
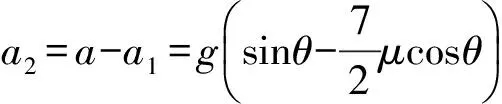
(14)

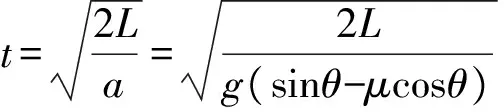
所以小球在斜面上運動的過程,摩擦力的作用點的位移不為0,因為摩擦產生的熱量為

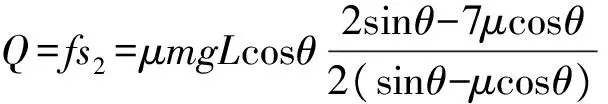
(15)

再從能量轉化的角度看,小球在斜面上運動的過程,重力勢能的減少量等于小球動能增加量與由于摩擦產生的內能(熱量)之和．所以有

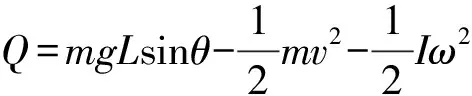
(16)

將v=at，ω=βt代入(16)式,可以驗證其結果與(15)式完全一致．這表明小球做又滾又滑運動時同樣遵從能量轉化和守恒定律．

綜上所述,小球在斜面上的運動與方形滑塊的運動存在著明顯的差別,運動能否等效與小球的半徑大小沒有任何關系,只有動摩擦因數足夠小時,兩者才能等效看待;小球運動時能量轉化的情況也與方形滑塊的運動顯著不同,但均遵從能量守恒定律;正確分析小球的運動,需用剛體平行平面運動的動力學知識.這顯然已經超出了中學要求,廣大中學物理教師在命制相關習題時一定要注意回避,以免出現科學性錯誤．

1 周衍柏.理論力學教程(第2版)[M].北京:高等教育出版社，1985:203.

本文是江蘇省教育科學“十二五”規劃課題“高中學生物理思維品質發展和分化現象的研究”(課題編號D/2013/02/571)階段性成果．

2017-02-13)