關于模糊數序列收斂性問題的研究

趙博,包玉娥

(內蒙古民族大學數學學院,內蒙古 通遼 028043)

關于模糊數序列收斂性問題的研究

趙博,包玉娥

(內蒙古民族大學數學學院,內蒙古 通遼 028043)

討論了模糊數序列在EW-型積分度量下的收斂性問題.首先給出了模糊數序列關于EW-型積分度量、水平EW-型度量以及水平EW-型測度收斂的概念;其次,討論了模糊數序列關于EW-型積分度量、下方圖度量以及水平度量收斂之間的關系,證明了在一定條件下模糊數序列關于EW-型積分度量、下方圖度量以及水平度量收斂的等價性.

模糊數序列;下方圖度量;EW-型積分度量;收斂性

1 引言

模糊數是實數域上的一類特殊的模糊集,在模糊分析學及其應用研究中起著非常重要的作用.在實際應用中,經常用模糊數來表示屬性決策領域中的許多決策信息[12].根據實際問題的需要,人們為了更好的研究模糊分析及其應用問題,在模糊數空間上定義了各種各樣的度量[3].從此,人們開始討論了模糊數空間的分析性質,給出了模糊數序列在各種度量之下的收斂性概念,為模糊分析及其應用問題的研究打下了良好的基礎[47].

區間數和模糊數的應用實際上均為屬性值為實數的信息系統在維度上的化簡,并且模糊數又可以用一族區間數來刻畫.文獻[910]中,建立了區間數空間上的EW-型積分度量及EW-型貼近度等概念,得到了一些有意義的結論.本文討論模糊數序列在EW-型積分度量之下的收斂性問題.

2 基本概念

設R為實數集.如果模糊集u：R→[0,1]是正規的,凸的上半連續的,且支集是緊集,則稱u為模糊數.模糊數全體構成的空間稱為模糊數空間,記為F0.

對于u∈F0,稱

為模糊數u的r-截集或r-水平集.

對任意的r∈[0,1],模糊數u的r-截集[u]r是實數集R上的一個非空有界閉區間.記為

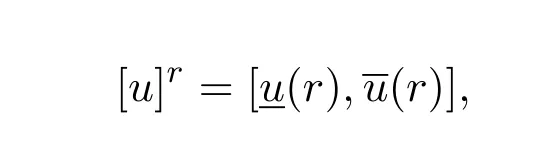
在F0上的序關系定義為：

對于u,v∈F0及k∈R,模糊數空間上的加法和數乘運算定義為：

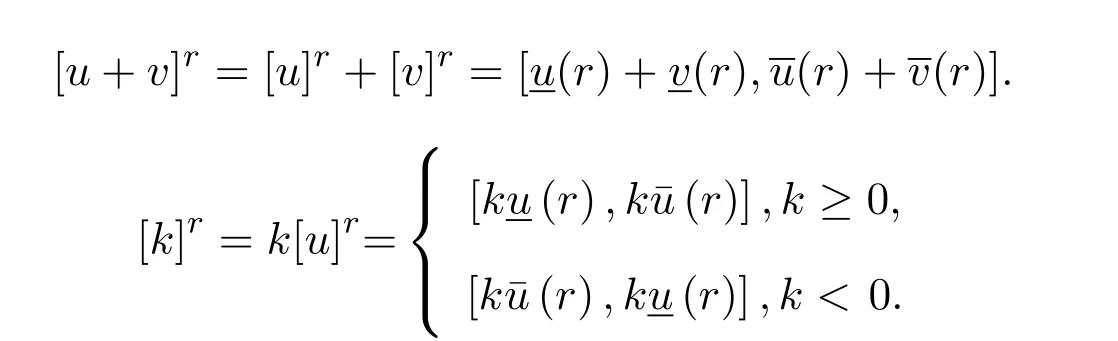
定義 2.1設(X,dH)是一個度量空間,A,B是X中的兩個非空緊集,則稱

為A和B的Hausdor ff度量,其中

定義 2.2[3]設u,v∈F0,則稱

為模糊數空間F0上的下方圖度量.其中

DH為定義R2在上的緊集族的Hausdor ff度量.

定義 2.3[3]設 uk,u ∈ F0(k=1,2,...),如果

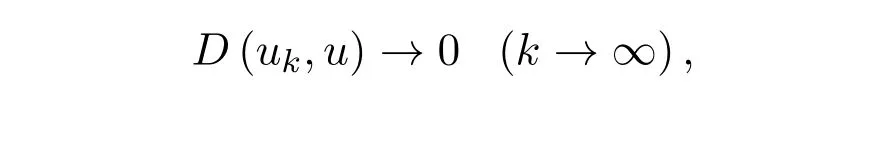
則稱模糊數序列{uk}依下方圖度量收斂于模糊數u,記為

定義 2.4[6]設 uk,u∈F0(k=1,2,...),如果對于任意的 r∈[0,1],有

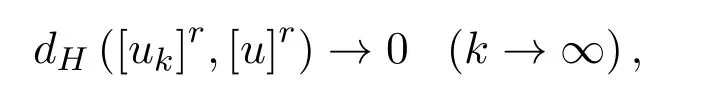
則稱模糊數序列{uk}依水平Hausdor ff度量收斂于模糊數u,記作

定義 2.5[6]設 uk,u ∈ F0(k=1,2,...),如果

關于r在[0,1]上幾乎處處成立,則稱模糊數序列{uk}依水平Hausdor ff度量幾乎處處收斂于模糊數u.

引理 2.1[6]若 uk,u∈F0(k=1,2,...),則以下結論等價：

(2)模糊數序列{uk}依Hausdor ff度量dH水平幾乎處處收斂于模糊數u;(3)對所有

其中

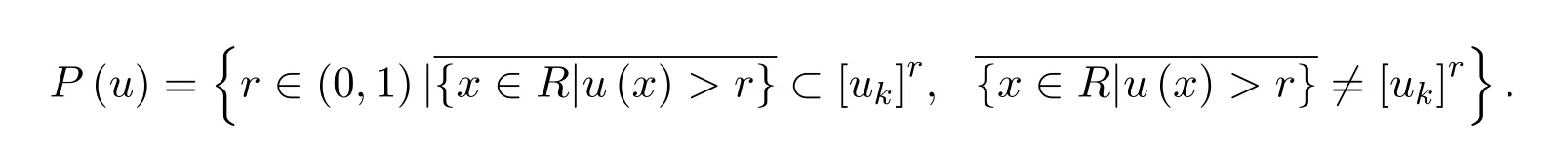
分別為區間數的期望值與寬度.

定理 2.1[9]設u,v∈F0,映射

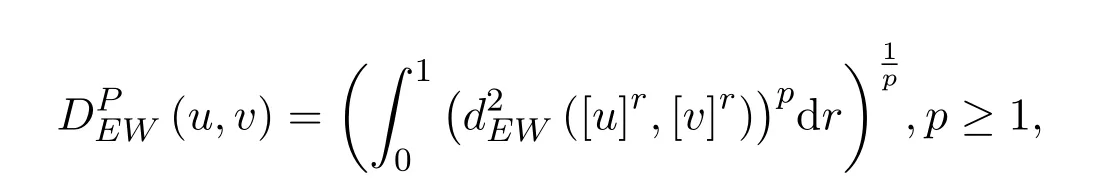
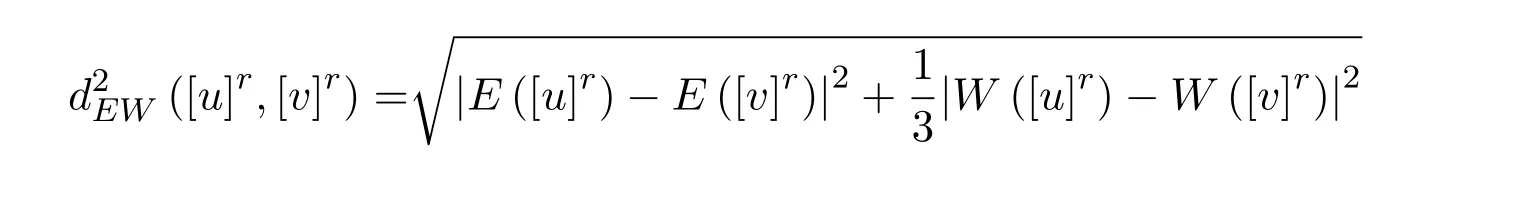
為區間數空間[R]上的EW-型度量.

定理2.2[10]設

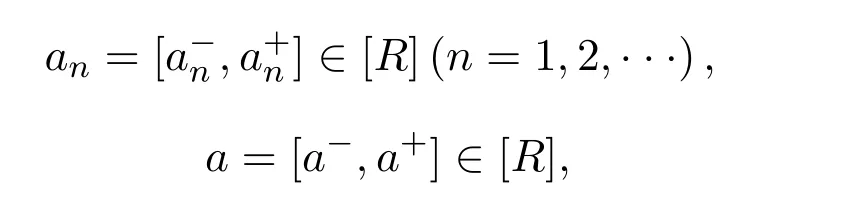
則區間數序列{an}依EW-型度量收斂于區間數a,即

3 EW-型積分度量空間上的收斂性

定義 3.1設 uk,u∈ F0(k=1,2,...),如果

則稱模糊數序列{un}依EW-型度量收斂于模糊數u,記作

定義 3.2設 uk,u∈F0(k=1,2,...),如果對于任意的 r∈[0,1],有

則稱模糊數序列{uk}依水平EW-型度量收斂于模糊數u,記作

定義 3.3設 uk,u∈F0(k=1,2,...),如果對于任意的 ε＞0和 η＞0,存在 k＞0,使得當 k≥K 時,有

其中m表示實直線R上的Lebesgue測度,則稱模糊數序列{uk}在EW-型度量下依測度收斂于模糊數u,記作

定理 3.1若uk,u∈F0(k=1,2,...),那么以下四個命題等價：

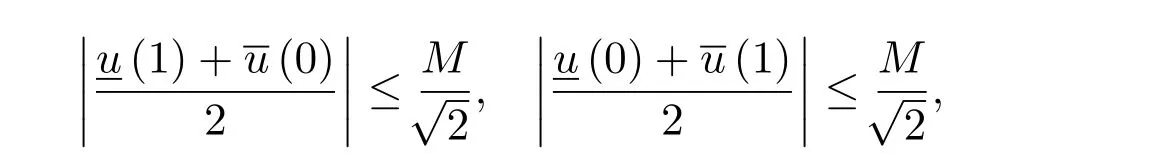
從而對任意的k＞0,有

又對任意r∈[0,1],由 [uk]1?[uk]r?[uk]0及[u]1?[u]r?[u]0,有

又因為

所以由引理 2.1,模糊數序列 {uk}依水平 Hausedor ff度量幾乎處處收斂于u.從而由定義 2.5,在[0,1]中存在零測度集?,使得

對任何r∈[0,1]?都成立.即

對任何r∈[0,1]?都成立.從而有

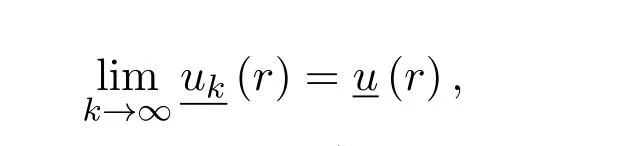
對任何 r∈[0,1]?都成立.于是對r∈[0,1]?,有

所以對 r∈[0,1]?,有

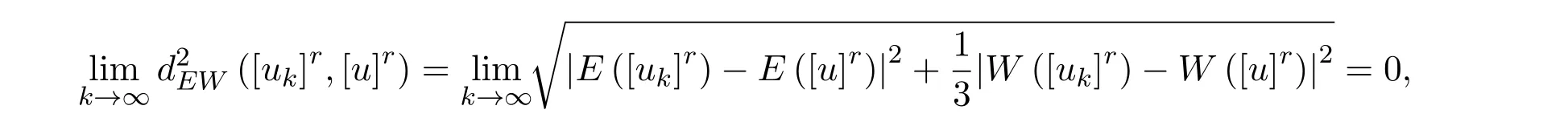
從而對任意的ε＞0,存在K＞0,使得當k＞K 時,有

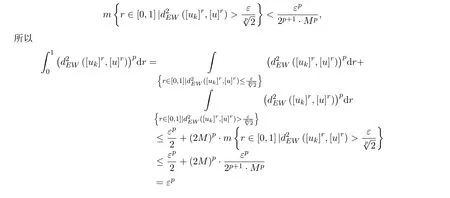
即對任意ε＞0,存在K＞0,使得當k＞K 時,有

從而

對任意ε＞0和η＞0,顯然有

由定義 3.3,有

其次利用反證法證明

假設存在r0∈(0,1),使得 [uk]r0在度量之下不收斂于[u]r0,則存在 ε0＞0和自然數列{kj}使得

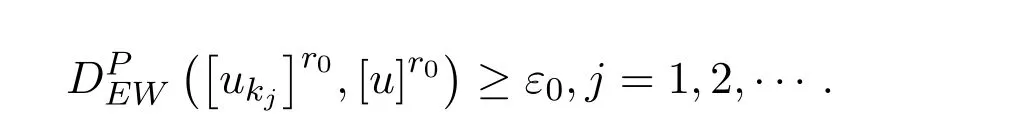
又由

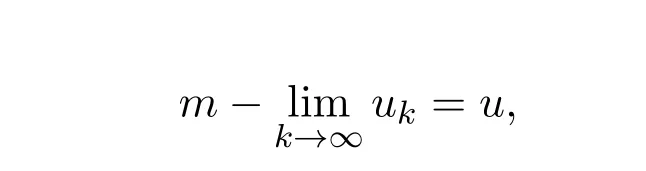
有

從而存在{ukj}的子列使得

關于r在[0,1]上幾乎處處成立.即存在??[0,1]且m(?)=0滿足

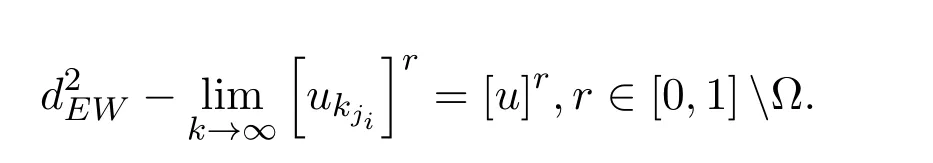
若r0∈?,則由u∈F0可知,對上述ε0＞0,存在對任意kji,有

對上述r1/∈?,存在K′＞0,當i≥K′時,有

從而當 i≥K′時,有

即

(4)?(1)根據下方圖度量的定義2.2,有

其中

參考文獻

[1]蘭蓉,范九倫.三角模糊數上的完備度量及其在決策中的應用[J].統工程學報,2010,3：314-319.

[2]Chen S M,Cheng S H,Lan T C.A novel similarity measure between intuitionistic fuzzy sets based on the centroid point so ftrans formed fuzzy numbers with applications to pattern cognition[J].Information Sciences,2016,344：15-40.

[3]Diamond P,Kloeden P.Metric Spaces of Fuzzy Sets：Theory and Applications[M].London：World Scienti fi c Publishing,1994.

[4]Wu C X,Wang G X.Convergence of sequence of fuzzy numbers and 1xed point theorems for increasing fuzzy mappings and application[J].Fuzzy Sets and Systems,2002,130：383-390.

[5]Fang J X,Huang H.On the level convergence of a sequence of fuzzy numbers[J].Fuzzy Sets and Systems,2004,147：417-435.

[6]Wu C X,Li H L,Ren X K.A note on the sendograph metric of fuzzy numbers[J].Information Sciences,2009,179：3410-3417.

[7]Huan H,Wu C X,Xie J L,et al.Approximation of fuzzy numbers using the convolution method[J].Fuzzy Sets and Systems,2017,310：14-46.

[8]雷一鳴,包玉娥.關于模糊數貼近度問題的研究[J].純粹數學與應用數學,2015,6：611-619.

[9]包玉娥,雷一鳴.模糊數空間上的積分度量及其在模糊聚類中的應用[J].模糊系統與數學,2017,4：133-139.

[10]包玉娥,彭曉芹,趙博.基于期望值與寬度的區間數距離及其完備性[J].模糊系統與數學,2013,6：133-139.

Study on the convergence problem of fuzzy number sequence

Zhao Bo,Bao Yu-e
(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)

In this paper,we discusses the convergence problem of the fuzzy number sequence on theEW-type integral metric.First we give the concept of the fuzzy number sequence ofEW-type integral metric,LevelEW-type metric and LevelEW-type metric convergence;Second,Discusses the relationship among the fuzzy number sequence on theEW-type integral metric and The fi gure below metric and the convergence of Level metric,and then prove the equivalence among the fuzzy number sequence on theEW-type integral metric and The fi gure below metric and the convergence of Level metric.

the fuzzy number sequence,the fi gure below metric,theEW-type integral metric,convergence

O159.2

A

1008-5513(2017)04-0340-12

10.3969/j.issn.1008-5513.2017.04.002

2017-07-07.

國家自然科學基金(11461052).

趙博(1987-),碩士,講師,研究方向：不確定性數學理論及應用.

2010 MSC:03E72