具有有限X-分解維數(shù)的模的同調(diào)性質(zhì)

王鵬飛,張翠萍

(西北師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,甘肅 蘭州 730070)

具有有限X-分解維數(shù)的模的同調(diào)性質(zhì)

王鵬飛,張翠萍

(西北師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,甘肅 蘭州 730070)

引入了左R-模M 關(guān)于可解模類X 以及內(nèi)射余生成子W 的同調(diào)維數(shù).給出了M 的X-分解維數(shù)有限的幾種刻畫,進(jìn)而討論了M 的這兩種維數(shù)之間的關(guān)系.研究了相對于有限W-分解維數(shù)的模的穩(wěn)定性以及相對于模類X 的模的穩(wěn)定性.

可解模類;同調(diào)維數(shù);X-分解維數(shù);W-分解維數(shù)

1 引言

設(shè)R是雙邊Noether環(huán).1969年,文獻(xiàn)[1]引入了有限生成模M 的Gorenstein維數(shù)G-dimRM,并證明了 G-dimRM ≤pdRM(當(dāng) pdRM ＜∞ 時,等號成立 ).他們還證明了廣義 Auslander-Buchshaum公式.1995年,文獻(xiàn) [2]在任意環(huán) R上引入了 Gorenstein投射模和 Gorenstein 投射維數(shù)GpdRM 的概念.稱左R-模M 是Gorenstein投射的,如果存在一個 HomR(-,Q)正合的正合列 ...→P1→P0→P0→P1→ ...,使得

其中 Q,Pi(i=0,1,...)是投射左 R-模.

GpdRM=inf{n∈Z|存在正合列 0→Gn→Gn?1→...→G1→G0→M →0,

如果這種正合列不存在,則規(guī)定

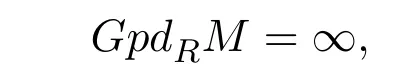
并且研究了這類模的相關(guān)同調(diào)性質(zhì).2010年,文獻(xiàn) [3]引入了 X-Gorenstein投射模的概念.隨著X的不同選取,X-Gorenstein投射模涵蓋了Gorenstein投射模[2],Ding投射模[4]和Gorenstein AC投射模.2014年,文獻(xiàn)[5]給出了Gorenstein投射維數(shù)有限的模的幾種等價條件,利用這些條件研究了有有限Gorenstein投射維數(shù)的模相對于有有限投射維數(shù)的模的穩(wěn)定性以及相對于Gorenstein投射模的穩(wěn)定性.受此啟發(fā),對于模類X 和W,本文引入X-分解維數(shù)和W-分解維數(shù)的概念,給出了左R-模M 的X-分解維數(shù)有限的幾種等價刻畫,并研究了這類模相對于有有限W-分解維數(shù)的模的穩(wěn)定性以及相對于模類X 的穩(wěn)定性.

以下R指有單位元的結(jié)合環(huán),模指左R-模.

2 模的 X-分解維數(shù)

定義 2.1設(shè)X 是一個左R-模類.稱X 是可解的,如果滿足下列條件：

(1)X 對擴(kuò)張封閉.即對任意左R-模的短正合列0→A→B→C→0,若A,C∈X,則

(2)X 關(guān)于滿同態(tài)核封閉.即對任意左R-模的短正合列0→A→B→C→0,若B,C∈X,則

(3)X 關(guān)于有限直和與直和項封閉.

定義 2.2設(shè)W 是模類X 的一個子類.稱W 是X 的內(nèi)射余生成子,如果滿足：

(1)對于任意的X∈X,存在左R-模的短正合列

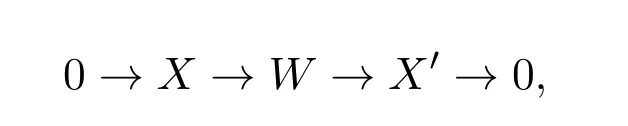
其中W ∈W,X′∈X.

(3)W 關(guān)于有限直和封閉.

定義 2.3設(shè)X 是可解模類,M 是左R-模,稱正合列

為M 的X-分解,其中Xi∈X(i=0,1,2,...).M 的X-分解維數(shù)(記為X-resdimRM)定義為：

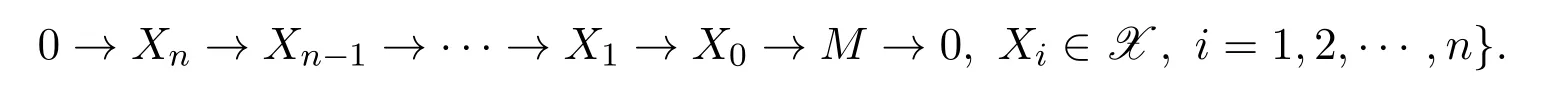
如果這種分解不存在,則規(guī)定

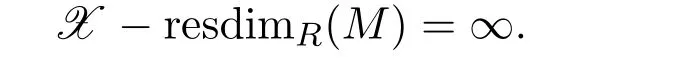
類似的可以定義M 的W-分解及其維數(shù).

以下用到的X 指可解左R-模類,W 指X 的內(nèi)射余生成子.

命題 2.1設(shè)n為非負(fù)整數(shù).則對任意的左R-模M,以下等價：

(1)X-resdimRM≤n.

(2)存在短正合列0→W→X→M→0,其中

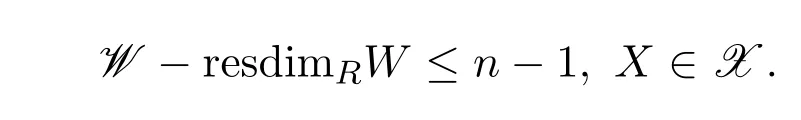
(3)存在短正合列0→M→W′→X→0,其中

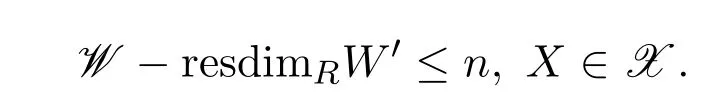
證明(1)? (2)用數(shù)學(xué)歸納法對 M 的維數(shù) n進(jìn)行歸納.當(dāng) n=0時,結(jié)論顯然成立.當(dāng)n=1時,有短正合列

其中Xi∈X,i=1,2.由X1∈X 可知存在短正合列

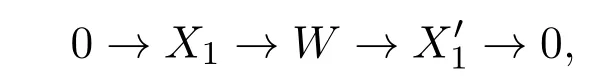
其中

考慮以下推出圖

從而

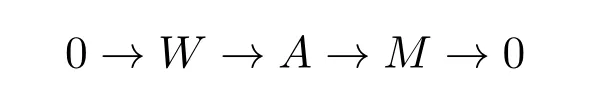
為所需短正合列.假設(shè)對X-分解維數(shù)不超過n-1(n≥2)的左R-模結(jié)論成立.下證對X-分解維數(shù)為n的左R-模,結(jié)論也成立.設(shè)

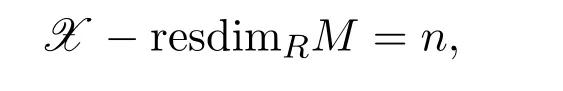
最后考慮以下推出圖：

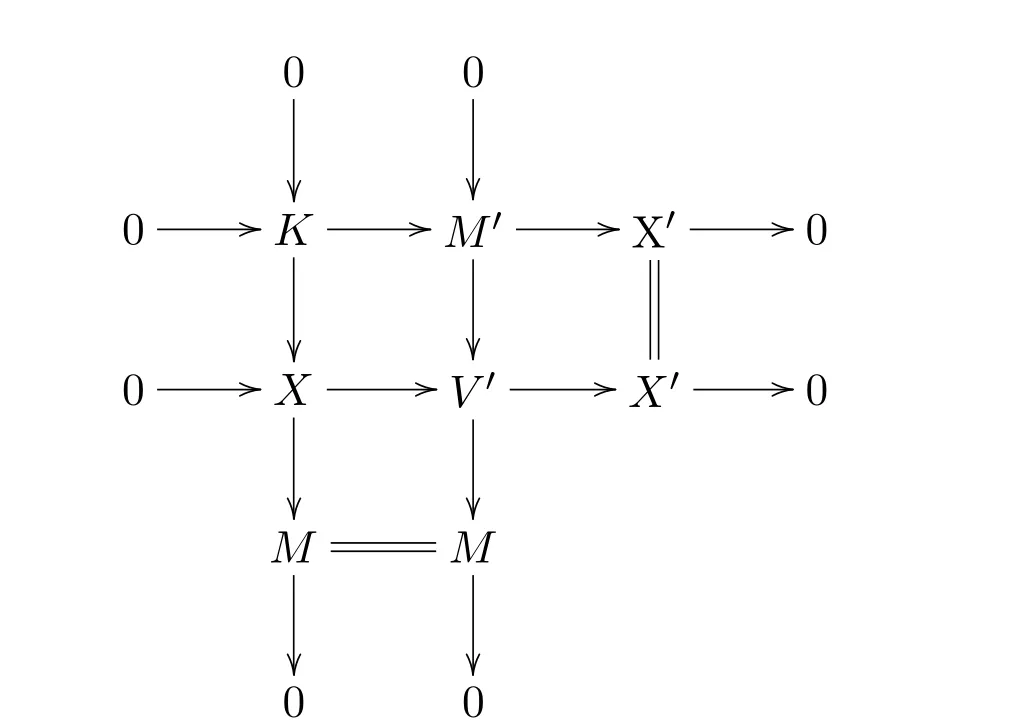
因為 X′,X ∈X,從而

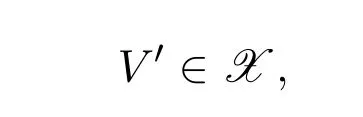
故第二列為所需短正合列.

(2)?(1)顯然.

(2)?(3)假設(shè)存在短正合列

故第一行為所需短正合列.

取X 為Gorenstein投射模做成的左R-模類,W 為投射模做成的左R-模類,故可得下列推論.

命題 2.2[5]設(shè)n為非負(fù)整數(shù).則對任意的左R-模M,以下等價：

(1)GpdRM≤n.

(2)存在短正合列0→K→G→M→0,其中G是Gorenstein投射左R-模,

(3)存在短正合列0→M →A→G′→0,其中G′是Gorenstein投射左R-模,

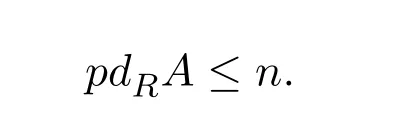
命題 2.3設(shè)左R-模M 的X-分解維數(shù)有限.

(1)若存在兩個短正合列

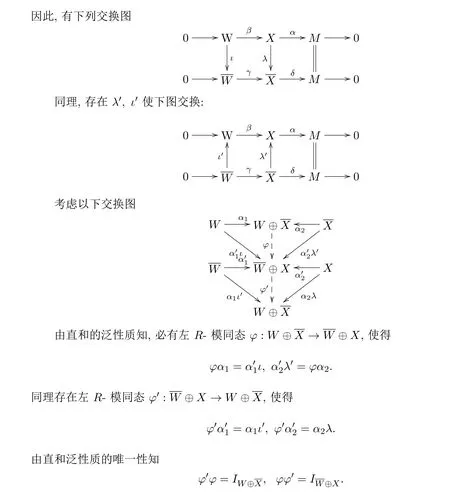
由此可知φ是同構(gòu),結(jié)論成立.

(2)證明與(1)類似.

3 相對于有限 W-分解維數(shù)的模的穩(wěn)定性

設(shè)M,N 是左R-模,易得集合H={f：M →N|f可通過一個有有限W-分解維數(shù)的左R-模分解}是Abel群HomR(M,N)的子群.W-HomR(M,N)表示商群HomR(M,N)/H,[f]W=[f]表示f所在的剩余類,其中f∈HomR(M,N).

引理 3.1設(shè)M,N,L是左R-模.則

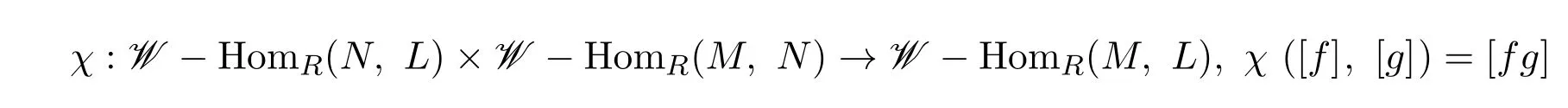
是映射.

證明設(shè)

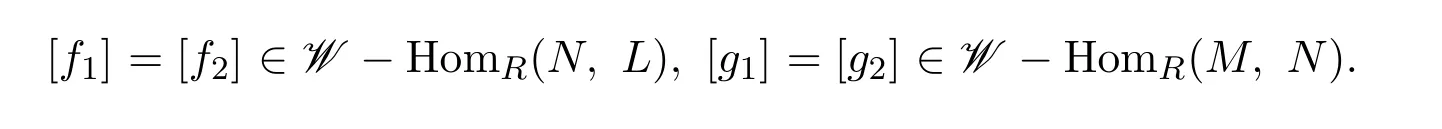
則f1-f2可通過有有限W-分解維數(shù)的左R-模W1分解,g1-g2可通過有有限W-分解維數(shù)的左R-模W2分解.不妨設(shè)

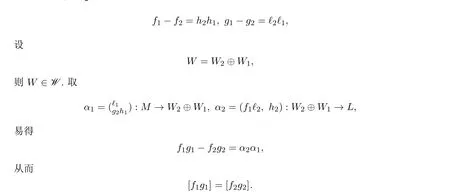
故χ是映射.

設(shè)W-R-Mod的對象為所有左R-模做成的類,對象M到N的態(tài)射集為W-HomR(M,N),態(tài)射的合成為引理3.1中定義的合成,則可得W-R-Mod為范疇.

引理 3.2設(shè)f：M →N 是一個左R-模同態(tài),其中M,N 的X-分解維數(shù)有限.考慮兩個短正合列

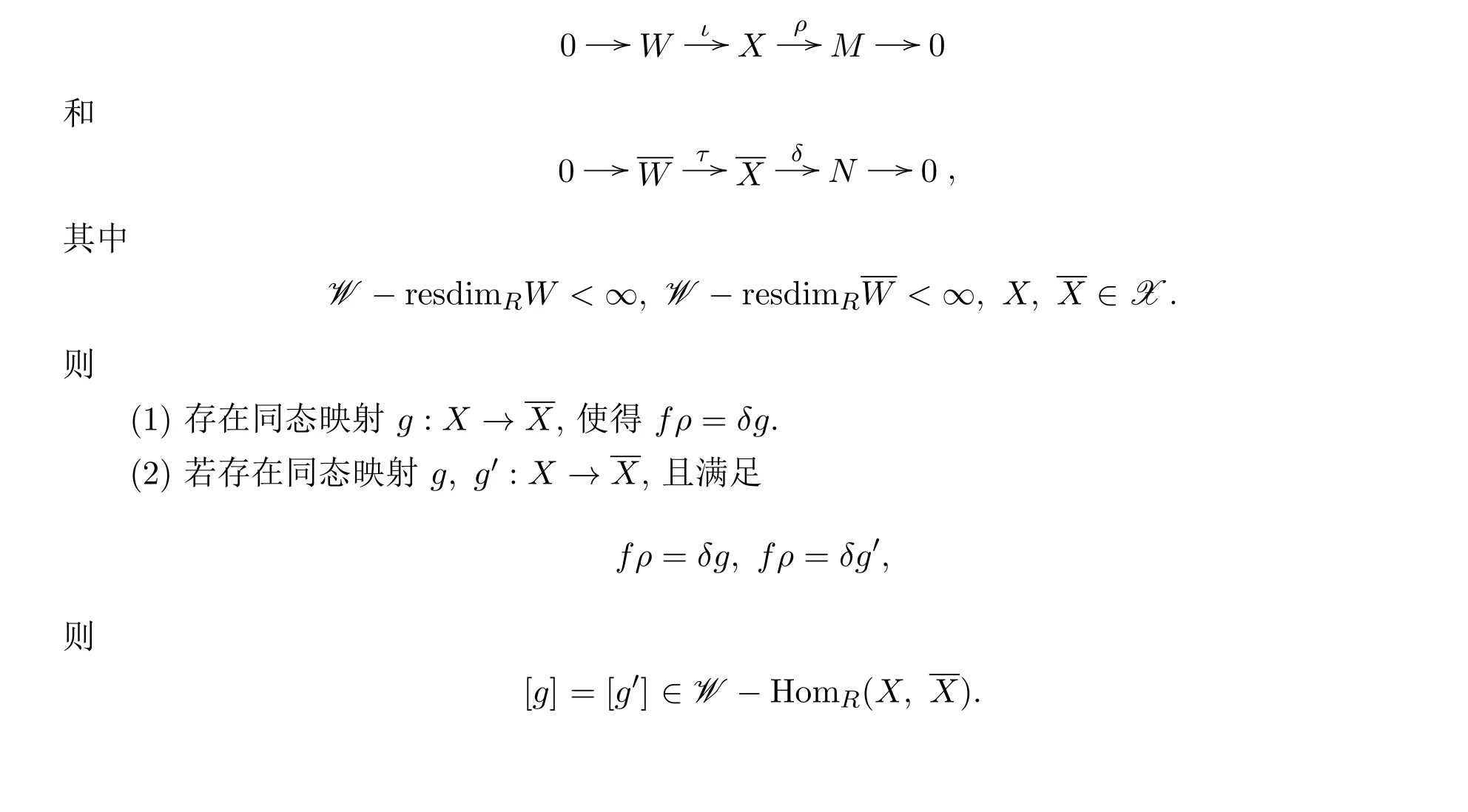
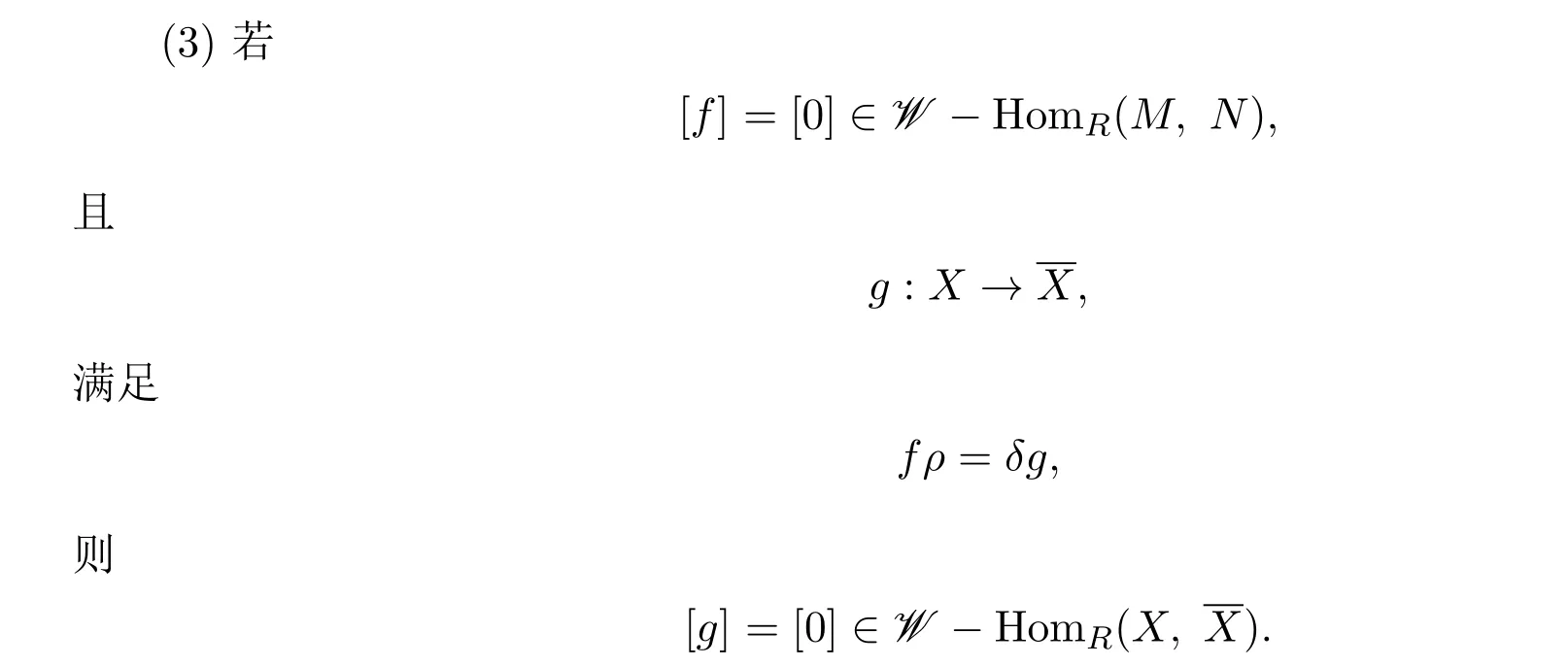
證明(1)因為X∈X,由維數(shù)轉(zhuǎn)移可得

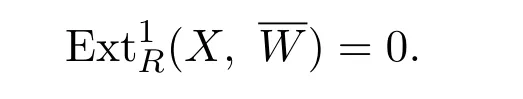
用HomR(X,-)作用短正合列,有短正合列

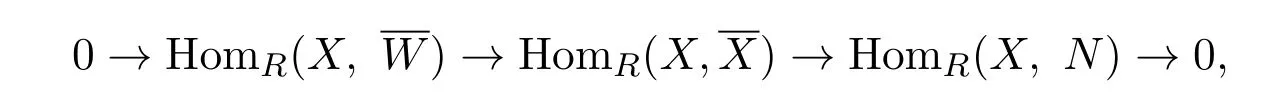
故結(jié)論成立.

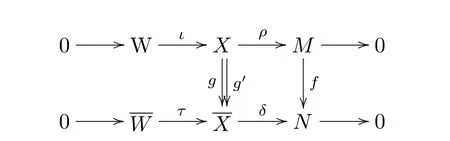
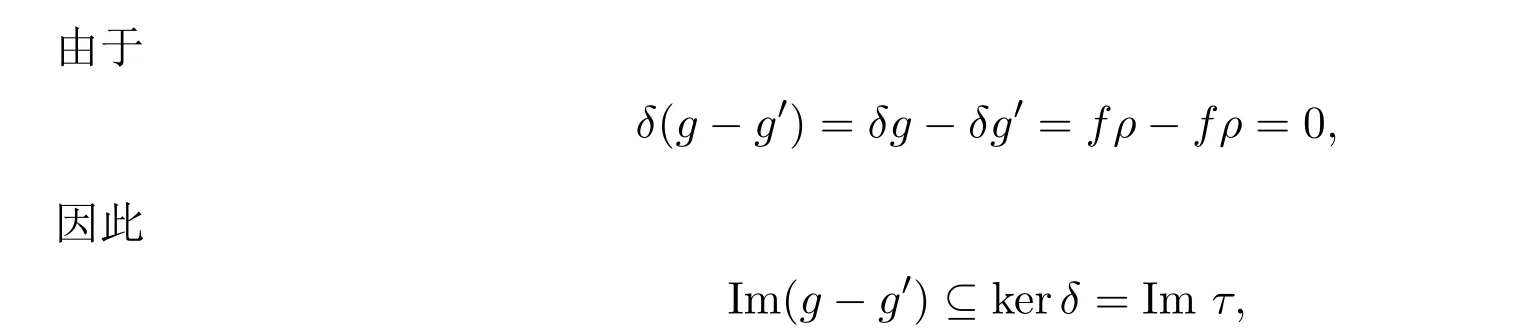
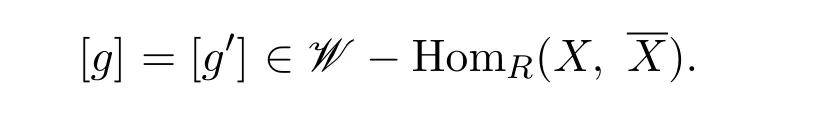
(3)假設(shè)f=ba,其中

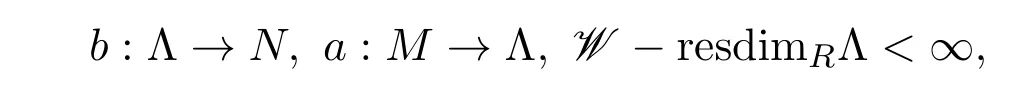
因此存在短正合列

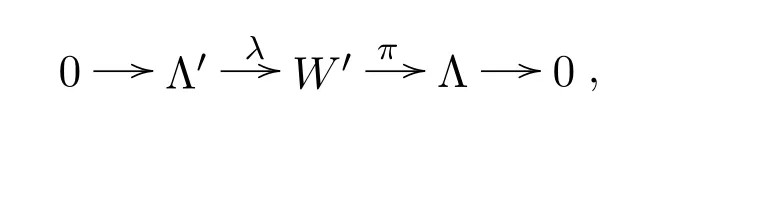
其中

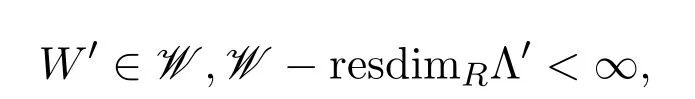
且

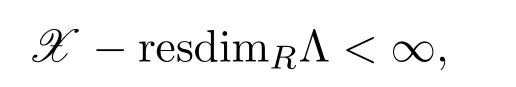
類似(1),存在同態(tài)映射α：X →W′,β：使下圖交換

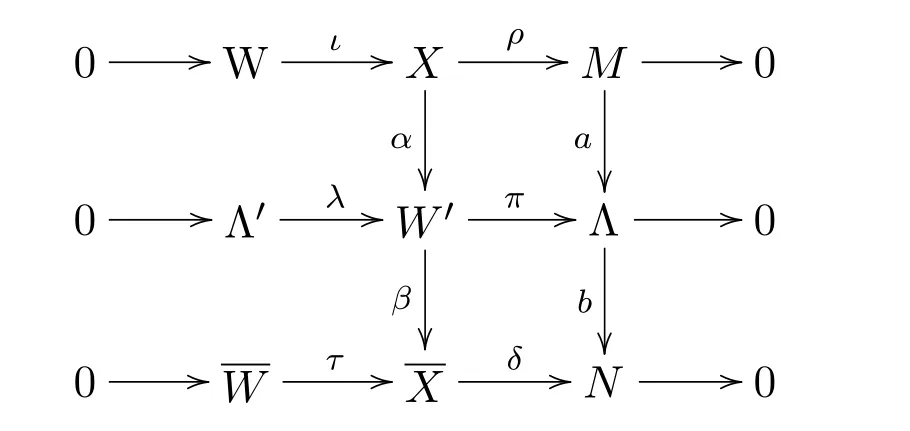
因為 W′∈W.所以 [βα]=[0].從而 [g]=[0].

FX-W(R)表示有有限X-分解維數(shù)的左R-模類,X-W(R)表示對象為X 中的模做成的類,則FX-W(R)和X-W(R)是W-R-Mod的滿子范疇,且X-W(R)是FX-W(R)的滿子范疇.由引理3.2,命題2.1可知,存在函子

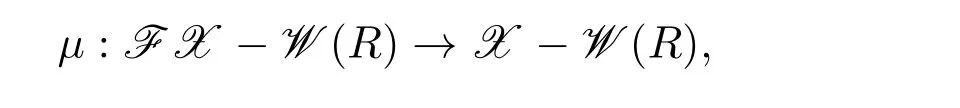
且有包含函子

定理 3.1函子μ是μ′的右伴隨對.

證明設(shè)G∈X-W(R),N∈FX-W(R).由命題2.1知,存在短正合列

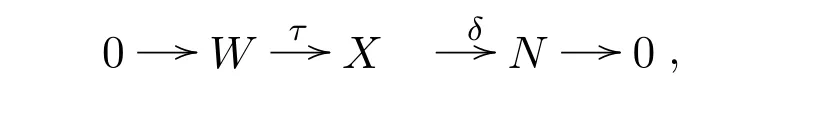
可得以下短正合列

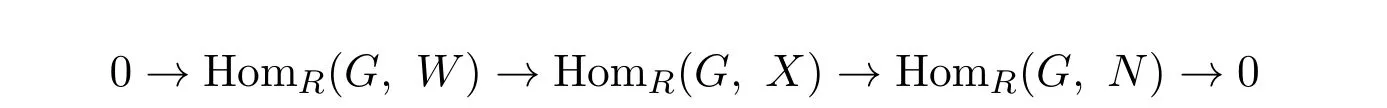
易得 [δ]?是滿的.

設(shè)g∈HomR(G,X),使得

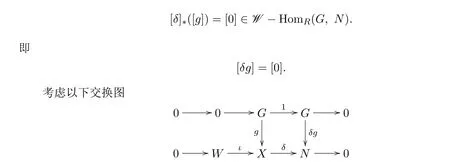
由定理 3.1(3)知 [g]=[0]∈ X-HomR(G,X),從而 [δ]?是單的.所以 [δ]?是一一映射.即

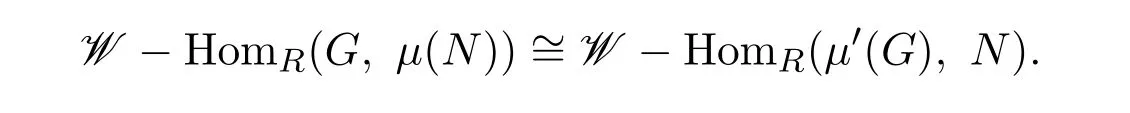
故μ是μ′的右伴隨對.

注 3.1如果X 為Gorenstein投射模做成的類,W 為有有限投射維數(shù)的左R-模做成的類.則范疇FX-W(R),X-W(R)分別為文獻(xiàn)[5]中的FP-FGP(R),FP-GP(R)范疇,從而文獻(xiàn)[5]可由定理3.1直接得到.

4 相對于模類X 的穩(wěn)定性

表示f所在的剩余類,其中

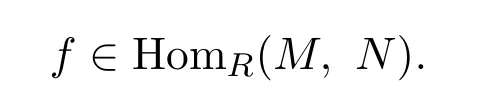
引理 4.1設(shè)f：M →N 是左R-模同態(tài),其中左R-模M,N 的X-分解維數(shù)有限.考慮兩個短正合列

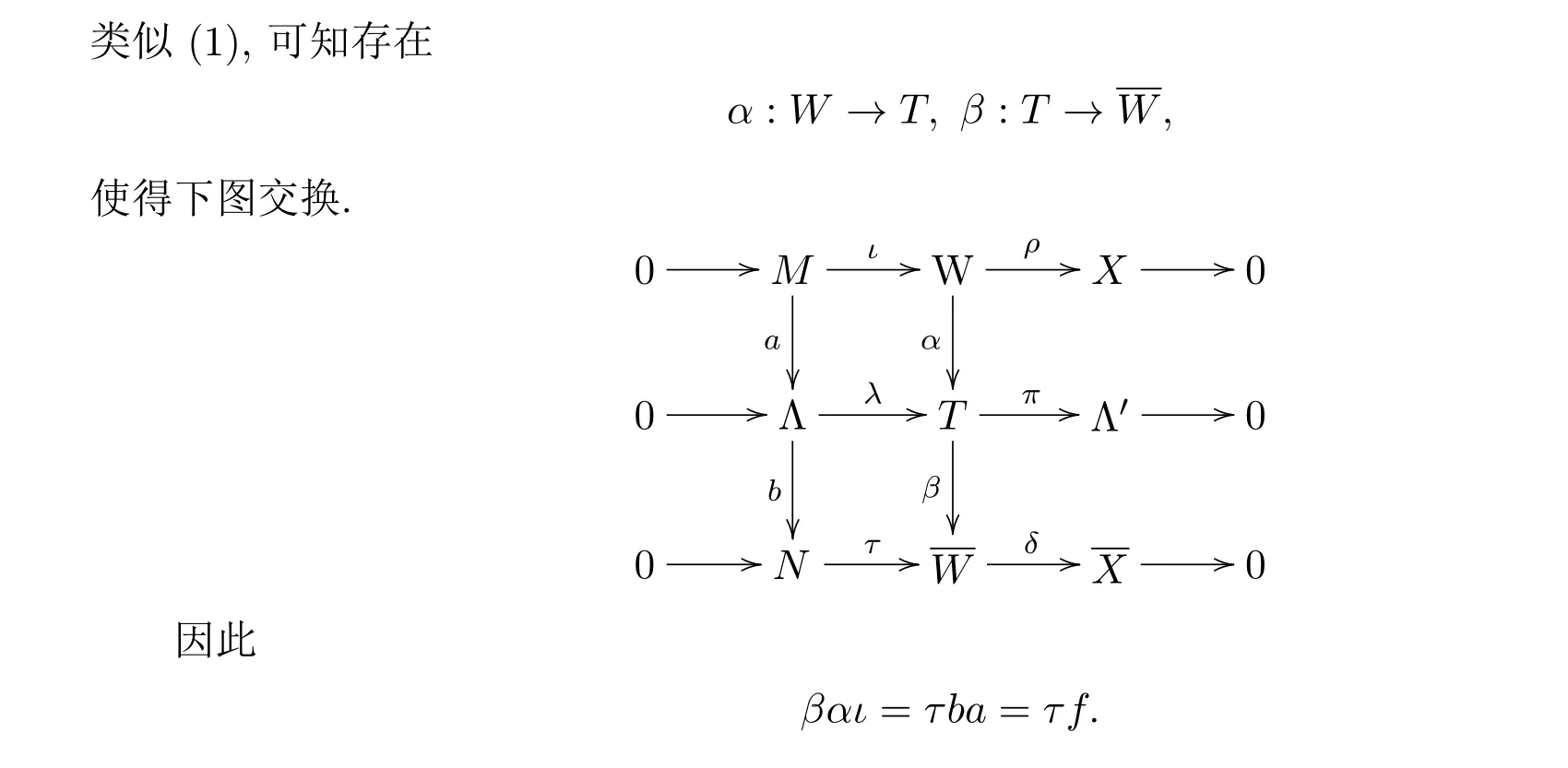
已知 τf=gι,所以

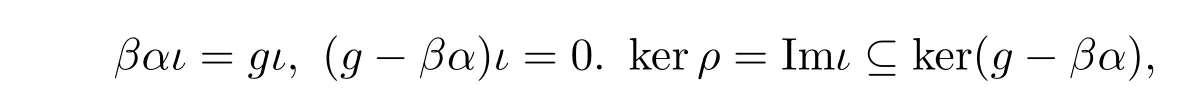
由同態(tài)基本定理知,存在唯一的同態(tài)映射

設(shè) X-R-Mod表示對象為所有左 R-模做成的類,對象 M 到 N的態(tài)射集為 XHomR(M,N),類似于引理3.1可得X-R-Mod是范疇.FX-X(R)表示有有限X-分解維數(shù)的左R-模類,FW-X(R)表示有有限W-分解維數(shù)的左R-模類,則FX-X(R)和FWX(R)是 X-R-Mod的滿子范疇.且FW-X(R)是FX-X(R)的滿子范疇.由引理4.1,命題2.1可知,存在函子

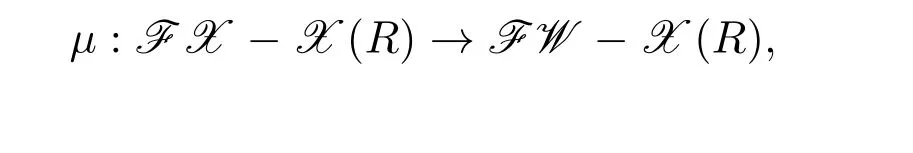
且有包含函子

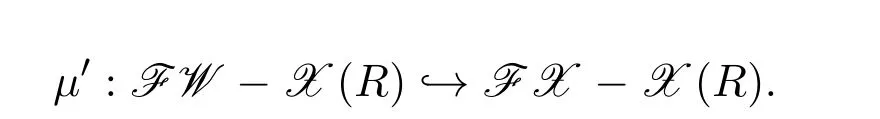
定理 4.1函子μ是μ′的左伴隨對.

證明設(shè)

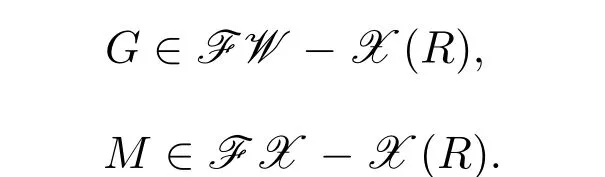
由命題2.1知,存在短正合列

考慮以下交換圖：

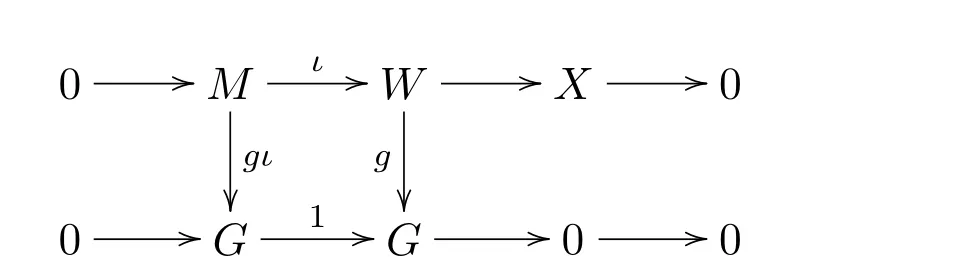
由引理4.1(3)知

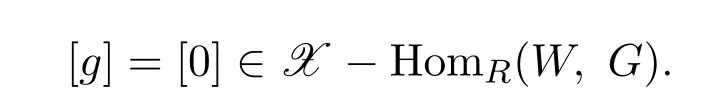
所以 [ι]?是單的.從而 [ι]?是一一映射,即

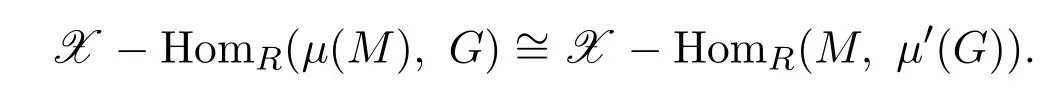
所以μ是μ′的左伴隨對.

注 4.1如果X 為Gorenstein投射模做成的類,W 為有限投射維數(shù)的左R-模做成的類.則范疇 FX-X(R),FW-X(R)分別為文獻(xiàn) [5]中的 FP-FGP(R),FP-GP(R)范疇,從而文獻(xiàn)[5,]可由定理4.2直接得到.

推論 4.1設(shè)M 為左R-模.若X-resdimRM ＜∞,則以下等價：

(1)M∈X.

(2)對于任意的左R-模B,W-resdimRB＜∞,有

[1]Auslander M,Bridger M.Stable Module Theory[M].New York：American Mathematical Society,1969.

[2]Edgar E E,Jenda O M G.Gorenstein injective and projective modules[J].Math.Z.,1995,220(4)：611-633.

[3]Bennis D,Ouarghi K.X-Gorenstein projective modules[J].Internat Math.Forum.,2010,5(10)：487-491.

[4]Ding N Q,Li Y L,Mao L X.Strongly Gorenstein fl at modules[J].J.Austral.Math.Soc.,2009,86(3)：323-338.

[5]Emmanouit I,Talelli O.Finiteness criteria in Gorenstein homological argebra[J].Trans.Amer.Math.Soc.,2014,366(12)：6329-6351.

Homology of fi niteness X-resolution dimensions of module

Wang Pengfei,Zhang Cuiping

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

This paper introduces the homological dimensions for left R-module M relative to resolving modules class X and injective cogenerators class.This paper presents some characterizations of fi niteness X-resolution dimensions to left R-module M,and the relation between X-resolution dimension and W-resolution dimension is also discussed.What’s more,it investigates the stability of modules with respect to fi niteness X-resolution dimensions and the stability of modules with respect to fi niteness W-resolution dimensions.

resolution modules class,homological dimensions,X-resolution dimensions,W-resolution dimensions

O178

A

1008-5513(2017)04-0406-18

10.3969/j.issn.1008-5513.2017.04.008

2017-04-17.

國家自然科學(xué)基金(11361051).

王鵬飛(1992-),碩士生,研究方向：同調(diào)理論.

2010 MSC:15A42