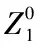應急物資儲備庫多級覆蓋選址問題與模型
(山東科技大學數學與系統科學學院 山東 青島 266590)
應急物資儲備庫多級覆蓋選址問題與模型
李瀟
(山東科技大學數學與系統科學學院山東青島266590)
覆蓋選址問題近年來已成為較為熱門的選址問題,覆蓋選址問題常用于應急領域,用以解決大規模災難發生時的應急物資供應調配。傳一般的覆蓋選址模型有兩個假設:(1)需求點的需求只能由一個設施滿足;(2)覆蓋半徑是固定的,只有在覆蓋半徑覆蓋范圍內,設施才能為其提供服務。
應急物流;選址;覆蓋;雙目標
對于大規模的突發事件,應急物流的主要目的是為了及時救援災害,減輕受災人員痛苦,及時提供大量的應急物資。考慮到這些特點,我們需要對傳統的覆蓋選址模型做出改變。
應急物流的基本特征是供應商和供應路線的變動性,屬于一種應急的打過模的特殊約束關系。應急物流落在應急二字上必須考慮時間效應,因為時間延遲可能導致生命損失,及時性是應急救援的首要原則,一些學者基于時間建立模型,構造了基于時間滿意度的最大覆蓋選址模型。
一、問題描述
某地區有n個應急物資儲備庫候選點和r個需求點,現要從這n個候選點中選擇p(p≤n)個建設應急物資儲備庫。某種自然災害突發,儲備庫損毀,道路損毀影響運輸,物資丟失,物資損壞,路況擁堵等,都會對應急物流造成影響,使需求點滿意度降低,另一方面,決策環境變化的不可控性,使決策必須在短時間內做出,災害的突發性及不確定性等,都使時間成為影響應急物流選址的重要因素。應急物流即物資的分配,物流與管理的過程,三者密不可分,相互作用,共同協調整合,對突發事件進行緊急響應和恢復。
二、模型假設
1.一個需求點在同一需求級別只有一個儲備庫為其服務,一個應急儲備庫可以服務多個需求點。
2.儲備路由于突發請情況受損后便“失效”,失效不可恢復,失效后將失去服務能力;
3.所有的儲備庫均可在任意點選址,各選址地點相互獨立,且失效概率相同
4.最多有k個應急物資儲備庫在一次災害中同時“失效”,因此需要為每個需求點按照不同的優先級分配k+1個應急物資儲備庫(k+1 5.每個需求點對應的應急儲備庫不能全部同時“失效”。 考慮一個應急物流網絡:Aj為第j(j=1,2,…,n)個儲備庫中的物資的庫存量;ai為第i(i=1,2,…,m)個需求點對物資的需求量;g(ωi)為滿意度函數,表示需求點i對物資的滿意程度,其中Qi為滿意度最大時的物資完好概率;p是準備建設的應急儲備庫的數目;Pr是級別為r的應急儲備庫為某個需求點提供服務的概率,且Pr=qr(1-q)k+1-r,其中q在某種災害中應急物資儲備庫“失效”的概率;f(tij)為時間滿意度函數。 模型中具體變量為如下:yj=1為在j地建設應急物資儲備庫,否則為0;xijr=1為需求點i由應急儲備庫j提供物資并且優先級別為r,否則為0。 建立突發災難下的應急物資儲備覆蓋選址模型: (1) (2) (3) (4) (5) (6) xijr,yj∈{0,1},i=1,2,…,m;j=1,2,…,n; r=1,2,…,k+1 (7) 目標函數(1)時間滿意度最大化,保證應急物流具有時效性;目標函數(2)各個物資需求點的滿意最大化,保證將優先的屋子合理的分配到需求的主體上;(3)需求點i在優先級r上有且只有一個應急設施為其提供服務,保證不造成資源的浪費且最大限度的發揮儲備庫的效用;(4)是指只有儲備庫被建立時才能為需求點提供服務,且每個需求點對應的應急儲備庫只能存在優先級,即各優先級的應急設施不能相同;(5)待建設的應急儲備庫的數量為p個;(6)是保證需求量不超過儲備庫的庫存量;(4.7)是決策變量。 所建的問題模型為多目標規劃模型,對于雙目標選址模型,一般思路即通過某種手段使其變為單目標參數規劃問題求解。本文所建的多目標模型用加權法轉化為單目標模型求解。 maxZ3=max(λ1Z1+λ2Z2) 其中λ1,λ2為加權系數,分別代表Z1,Z2的不同權重。轉化為: maxZ3=max(λ1Z1+λ2Z2) s.t. 式(4.3)~(4.7) 對模型進行加權 使 第一步:將多目標模型(P1)分別看成兩個單目標模型,即 s.t. 式(3)~(7) s.t. 式(3)~(7) 第二步:通過λ-加權法確定λ1和λ2; 第三步:應用lingo軟件對問題(P2)進行求解,得問題(P1)的最優解。 李瀟(1993-),女,漢族,山東濟寧人,山東科技大學,在讀研究生,研究方向:運籌與管理科學。三、符號說明及模型建立


四、模型分析
五、模型求解