帶有兩個加性時變時滯系統的穩定性分析
于雪梅, 王曉梅, 鐘守銘
(電子科技大學 數學科學學院, 四川 成都 611731)
帶有兩個加性時變時滯系統的穩定性分析
于雪梅, 王曉梅*, 鐘守銘
(電子科技大學 數學科學學院, 四川 成都 611731)
研究帶有2個加性時變時滯系統的穩定性問題.首先,研究系統的時滯依賴穩定,并將整個時滯區間分成若干個小區間,在此條件下構造合適的Lyapunov函數.其次,根據Lyapunov穩定性理論,結合不等式技巧得到系統漸近穩定的充分條件,推廣了現有文獻的相關內容,并且用一系列線性矩陣不等式表示這些結論.最后,用一個數據例子證實了該研究方法的有效性.
時滯系統; 時滯依賴; Lyapunov函數; Lyapunov穩定性理論
近年來,時滯系統引起了科學界的普遍關注和研究.時間滯后簡稱時滯,時滯是指某一行為從開始到產生結果的時間段,比如一個瞬間或一個動作時段.時滯普遍存在于實際系統中,并且時滯系統已經廣泛地應用于許多實際應用中,如通訊、經濟系統、網絡控制系統、渦輪噴氣發動機、生產系統、神經網絡、生物和化學工程系統等.時滯通常是引起系統不穩定的重要原因之一,甚至給系統性能造成不良影響,因而,對時滯系統進行穩定性分析具有重要意義.目前,可以看到有許多對時滯系統穩定性的研究[1-3].
根據系統穩定是否受時滯影響,時滯系統的穩定性可以分為時滯依賴穩定和時滯獨立穩定.時滯依賴穩定是指系統穩定與時滯有關,時滯獨立是指系統穩定與時滯無關.時滯獨立穩定條件相對時滯依賴穩定較為保守,特別是當時滯相對小的系統.目前時滯系統穩定性結論多數都是時滯獨立的.因而,時滯依賴穩定的研究引起了人們更多的關注[4-9].
本文研究帶有2個加性時變時滯系統的時滯依賴穩定性問題.為了獲得較小保守性,將考慮帶有2個加性時滯的系統.文獻[10]在沒有引入松弛變量的情況下用凸多面體法獲得了新的穩定性結論;文獻[11]通過引入松弛變量獲得了不同的穩定性結論;文獻[12]通過構造一個新的Lyapunov函數獲得了時滯系統的穩定性結論;文獻[13]對系統進行了穩定性分析,獲得了時滯依賴穩定性結論.然而,文獻[10-13]在構造Lyapunov函數時,要求Lyapunov函數中的每部分都正定.通常Lyapunov函數正定并不一定要求每部分都正定,因此,在現有的一些文獻中這方面有很大的研究和改進空間.
本文首先分析了系統的時滯依賴穩定.然后,通過將整個時滯區間分成若干個小的時滯區間,并根據時滯狀態x(t-h1)、x(t-h2)和x(t-h)構造了一個新的Lyapunov函數.在構造Lyapunov函數時并不要求它的每部分都正定,而是保證整體正定.另外,在對Lyapunov函數求導后討論其上界過程中,不同的區間引入不同的松弛變量,從而獲得一個相對嚴格的上界.依賴于2個時滯,根據Lyapunov穩定性理論,結合不等式技巧獲得了系統漸近穩定的充分條件.新的穩定性結論降低了保守性.最后,用一個數值例子說明結論的有效性.
1 問題描述和準備
本文中,矩陣的上標“T”代表轉置,I是一n×n單位矩陣,Ei代表diag{In,In,In,In,In,In,In}的第i行且Eij=Ei-Ej(i,j=1,2,…,7).X和Y是對稱矩陣,X>Y(X≥Y)代表X和Y的對應元素滿足>(≥).特別地,如果X>0,X為正矩陣.“*”代表矩陣的對稱元.
考慮如下時滯系統:
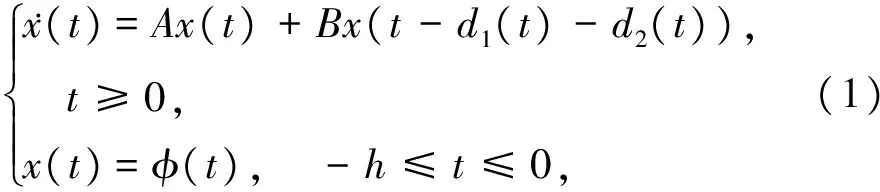
其中,x(t)∈Rn是系統的狀態向量,A,B∈Rn×n是已知常矩陣,φ(t)是初始條件,d1(t)和d2(t)是時滯,滿足
則系統(1)可改寫為
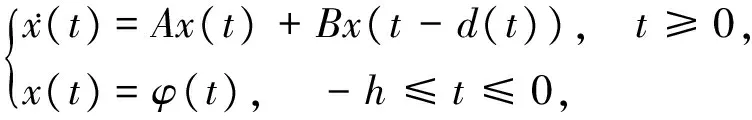
(2)
其中
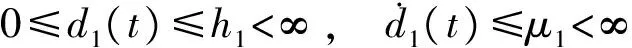
(3)
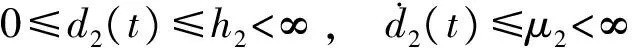
(4)

(5)
h=h1+h2,μ=μ1+μ2.
(6)
注 1 通常不同的時滯具有不同的性質,因而不能直接把時滯簡單的加一起.并且d(t)的最大值通常小于h=h1+h2,因此用h=h1+h2作為d(t)的上界不夠嚴謹.以下將考慮帶有2個加性時滯系統(1)并獲得新的穩定性結論.
引理 1.1[14]設對任意的正定矩陣M>0,存在常量α>0和向量函數ω,且ω:[0,α]→Rn,那么有不等式
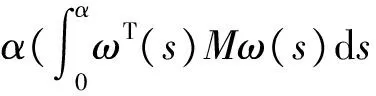
(7)
2 主要結果
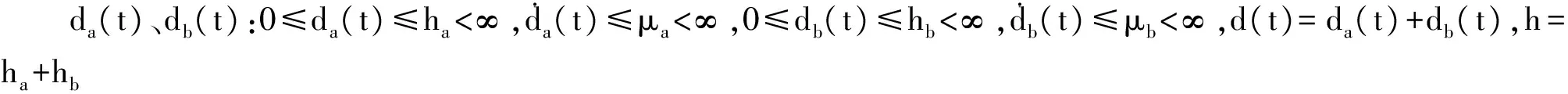
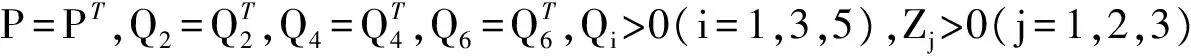
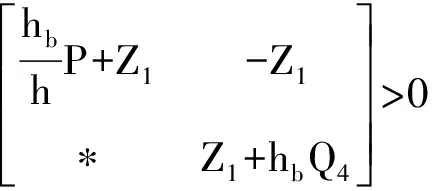
(8)
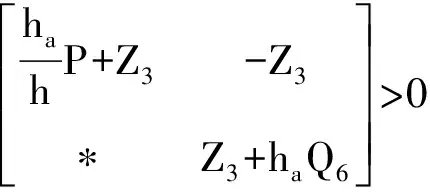
(9)
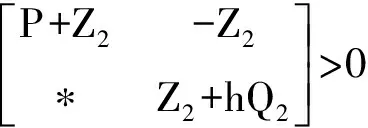
(10)
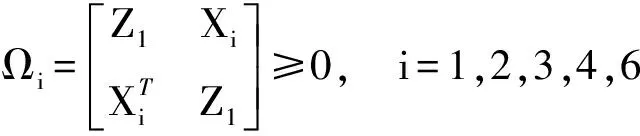
(11)
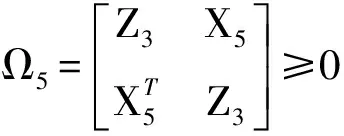
(12)
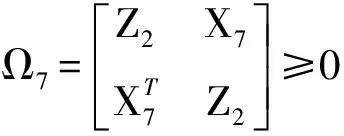
(13)
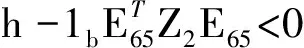
(14)
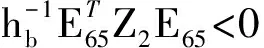
(15)
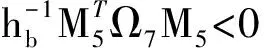
(16)
其中
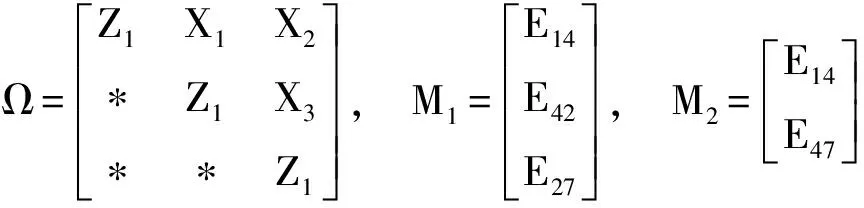
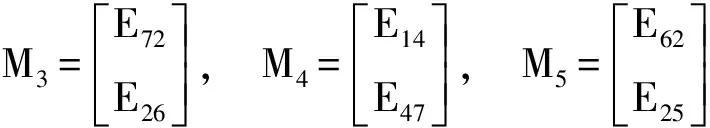
并且
Φ=Γ+ΞTΠΞ,

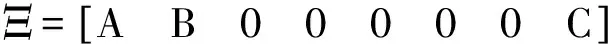
Π=[hbZ1+(ha-hb)Z3+hbZ2],
φ11=PA+ATP+Q1+Q3+Q4+Q5,
φ22=-(1-μ)Q3, φ33=-(1-μa)Q1,
φ44=-(1-μb)Q5, φ55=-Q2,
φ66=Q2-Q6, φ77=Q6-Q4,
其中(6)式給出了h和μ的表示.
證明 根據ha=max(h1,h2)和hb=min(h1,h2),可將區間[-h,0]分成小區間[-h,-ha]、[-ha,-hb]和[-hb,0],構造Lyapunov函數
V(t):=V1(t)+V2(t)+V3(t)+V4(t),
(17)
其中
V1(t)=xT(t)Px(t),
(18)
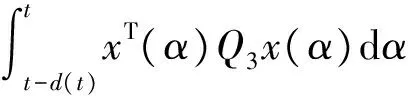
(19)
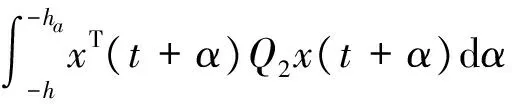
(20)
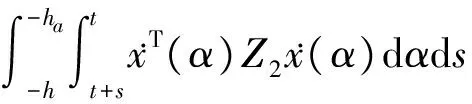
(21)
其中d(t):=d1(t)+d2(t).
首先證明Lyapunov函數V(t)是正定的.根據引理1.1可得
x(t+s)]TZ1[x(t)-x(t+s)]ds,
(22)
x(t+s)]TZ3[x(t)-x(t+s)]ds,
(23)
x(t+s)]TZ2[x(t)-x(t+s)]ds,
(24)
且有
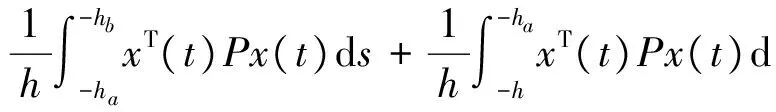
根據Qi>0(i=1,3,5),由(17)~(25)式有
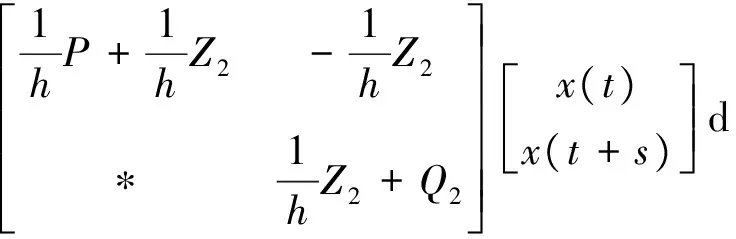
根據(8)~(10)式可知Lyapunov函數V(t)是正定的.沿著系統(1)的軌跡對V(t)求導,則有
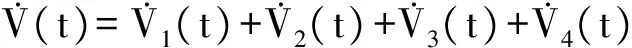
(26)
其中
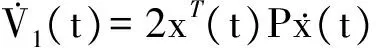
(27)
xT(t)Q5x(t)+xT(t)Q3x(t)-
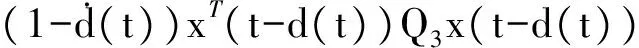
(28)
xT(t-hb)Q6x(t-hb)-xT(t-ha)Q6x(t-ha)+
xT(t-ha)Q2x(t-ha)-xT(t-h)Q2x(t-h),(29)
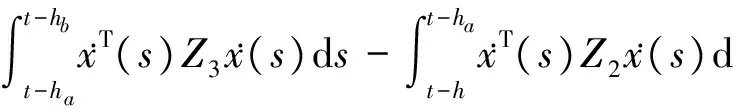
根據(26)~(30)式有
[Ax(t)+Bx(t-d(t))]TPx(t)+
xT(t)[Q1+Q3+Q4+Q5]x(t)-
(1-μa)xT(t-da(t))Q1x(t-da(t))-
(1-μb)xT(t-db(t))Q5x(t-db(t))-
(1-μ)xT(t-d(t))Q3x(t-d(t))+
xT(t-hb)[Q6-Q4]x(t-hb)+
xT(t-ha)[Q2-Q6]x(t-ha)-
xT(t-h)Q2x(t-h)+
[Ax(t)+Bx(t-d(t))]T×
[hbZ1+(ha-hb)Z3+(h-ha)Z2]×
[Ax(t)+Bx(t-d(t))]-
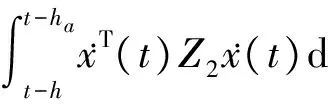
(31)
情形1 d(t)≤hb,由引理1.1可得
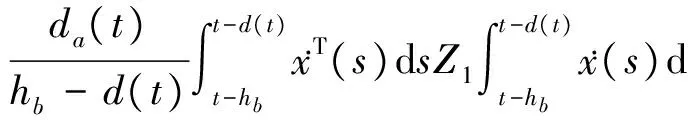
(32)
由
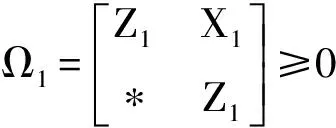
可得
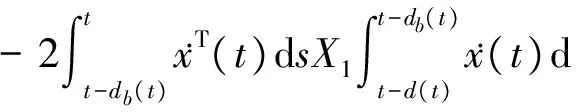
(33)
相似地有:
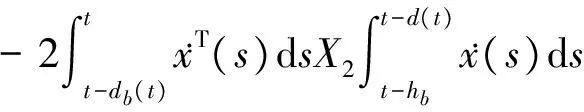
(34)
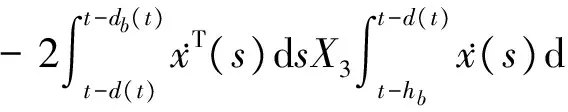
(35)
由(32)~(35)式可得:
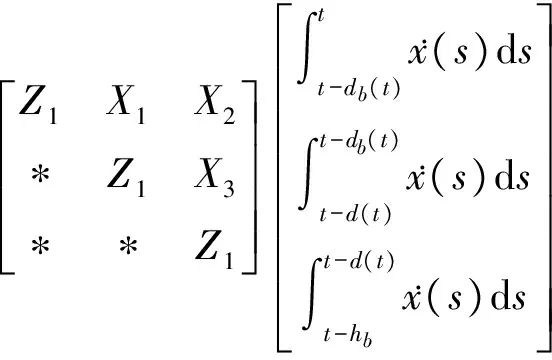
(36)
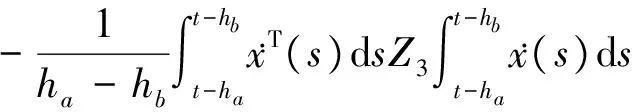
(37)
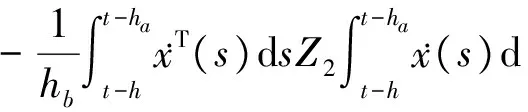
(38)
定義
ζ(t):=[xT(t),xT(t-d(t)),
xT(t-da(t)),xT(t-db(t)),
xT(t-h),xT(t-ha),xT(t-hb)]T.
將(36)~(38)式代入(31)式,則
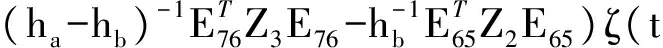
因此,由(14)式知
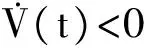
情形 2 hb 相似于(32)式有: 則 情形3 ha 相似于(32)式有: 則 因此,由(16)式知 注 2 事實上 如果P>0,Zj>0(j=1,2,3)和Qi>0(i=1,2,…,6),則這些條件保證了Lyapunov函數V(t)是正定的,顯然滿足(8)~(10)式.所以得到以下推論. 推論 2.1 對于給定的h1和h2,h1>h2,μ1和μ2,假設系統(1)滿足(3)和(4)式,如果存在矩陣P>0,Qi>0(i=1,…,6),Zj>0(j=1,2,3)和Xk(k=1,2,…,7),則系統(1)是漸近穩定的,那么有如下線性矩陣不等式: 其中 并且Φ=Γ+ΞTΠΞ, Π=[h2Z1+(h1-h2)Z3+h2Z2], φ11=PA+ATP+Q1+Q3+Q4+Q5, φ22=-(1-μ)Q3, φ33=-(1-μ1)Q1, φ44=-(1-μ2)Q5, φ55=-Q2, φ66=Q2-Q6, φ77=Q6-Q4, 其中(6)式給出了h和μ的表示. 考慮系統(1),給出以下參數: 表 1 計算時滯d2(t)的上界h2 本文研究帶有2個加性時滯系統的時滯依賴穩定性問題.在將整個區間分為若干個小區間的基礎上,通過構造一個改進的Lyapunov函數,研究了時滯依賴穩定性.一方面,在保證Lyapunov函數正定的條件下,要求其導函數也是正定的.當構造Lyapunov函數時,保證Lyapunov函數整體是正定的,但不要求其每部分都正定.另一方面,為了降低保守性,在計算Lyapunov函數的導函數的上界時,相對于不同的區間,引入不同的松弛變量,從而獲得更嚴格的上界,并得到系統漸近穩定的充分條件.最后用Matlab LMI工具箱給出一個數值比較說明結論的有效性. 表 2 計算時滯d1(t)的上界h1 [1] RAMAKRISHNAN K, RAY G. Stability criteria with less LMI variables for linear system with additive time-delays[J]. J Appl Math Comput,2011,36(1/2):263-274. [2] PENG C, YANG T C. Event-triggered communication andH∞control co-design for networked control systems[J]. Automatica,2013,49(5):1326-1332. [3] 裴冀南. 具有時滯的線性系統的漸近穩定[J]. 四川師范大學學報(自然科學版),2001,24(2):151-153. [4] DEY R, RAY G, GHOSH S, et al. Stability analysis for continuous system with additive time-varying delays:a less conservative result[J]. Appl Math Comput,2010,215(10):3740-3745. [5] FRIDMAN E, SHAKED U. Delay-dependent stability andH∞control:constant and time-varying delays[J]. Inter J Control,2003,76(1):48-60. [6] LI X, DE SOUZA C E. Delay-dependent robust stability and stabilization of uncertain linear delay system:a linear matrix inequality approach[J]. IEEE Trans Automatic Control,1997,42(8):1144-1148. [7] SHAO K Y, ZHANG H Z, ZHAO W C, et al. Delay-dependent robust stabilization of uncertain state-delayed systems[J]. Inter J Control,2004,74(14):1447-1455. [8] ZHANG C K, HE Y, JIANG L, et al. Delay-dependent stability criteria for generalized neural networks with two delay components[J]. IEEE Trans Neural Networks Learning Systems,2014,25(7):1263-1276. [9] SHAO H. Improved delay-dependent stability criteria for systems with a delay varying in a range[J]. Automatica,2008,44(12):3215-3218. [10] SHAO H Y, ZHANG Z Q, ZHU X L, et al.H∞control for a networked control model of systems with two additive time-varying delays[J]. Abst Appl Anal,2014,2014(349):2618-2623. [11] LIU P L. Further results on delay-range-dependent stability with additive time-varying delay systems[J]. Isa Transactions,2014,53(2):258-266. [12] GAO H, CHEN T, LAM J. A new delay system approach to network-based control[J]. Automatica,2008,44(1):39-52. [13] LAM J, GAO H J, WANG C H. Stability analysis for continuous systems with two additive time-varying delay components[J]. Syst Control Lett,2007,56(1):16-24. [14] GU K. An integral inequality in the stability problem of time-delay systems[C]//Proc 39th IEEE Conf Decision and Control. New York:IEEE,2000:2805-2810. [15] WU M, HE Y, SHE J H, et al. Delay-dependent criteria for robust stability of time-varying delay systems[J]. Automatica,2004,40(8):1435-1439. [16] JING X J, TAN D L, WANG Y C. An LMI approach to stability of systems with severe time-delay[J]. IEEE Trans Automatic Control,2004,49(7):1192-1195. [17] LEE Y S, MOON Y S, KWON W H. Delay-dependent robustH∞control for uncertain systems with time-varying state-delay[C]//Proc 40th SICE Ann Conf. New York:IEEE,2001:198-203. 2010 MSC:93D05; 93D20 (編輯 周 俊) Stability Analysis for Systems with Two Additive Time-varying Delays YU Xuemei, WANG Xiaomei, ZHONG Shouming (CollegeofMathematicsScience,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,Sichuan) The problem of delay-dependent stability for systems with two additive time-varying delay is investigated. Firstly, the delay-dependent stability is studied and the whole delay interval is divided into subintervals. Based on the above condition, a novel type of Lyapunov function is presented. Secondly, a sufficient condition for asymptotic stability of the system is obtained by using Lyapunov stability theory and inequality technique. The relevant contents of the existing literature are generalized. And this criterion is given as a set of linear matrix inequalities. Finally, a numerical example is given to support the effectiveness of the proposed method. delay system; delay-dependent; Lyapunov function; Lyapunov stability theory 2016-01-21 國家自然科學基金(61273015)、安徽省高校自然科學基金重點項目(KJ2016A555和KJ2016A625)和安徽省中青年優秀人才基金(GXYQ2017158) O231 A 1001-8395(2017)04-0427-08 10.3969/j.issn.1001-8395.2017.04.001 *通信作者簡介:王曉梅(1969—),女,副教授,主要從事混合動力系統及其控制、神經網絡、生物模型等的研究,E-mail:xmwang16@126.com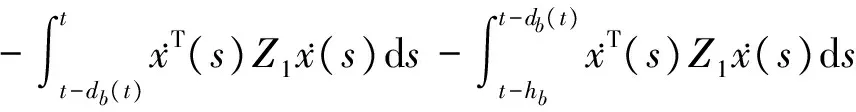

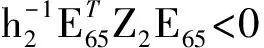
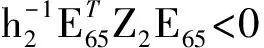
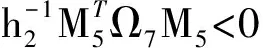
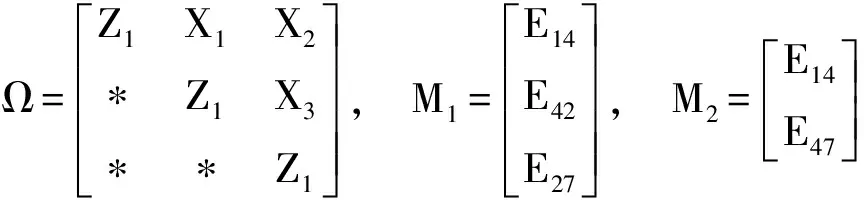
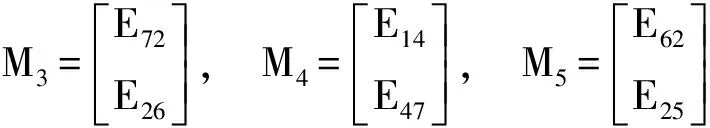

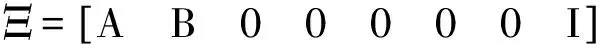
3 數值實例
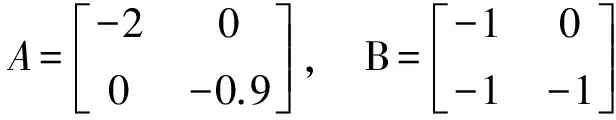
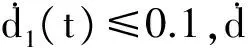
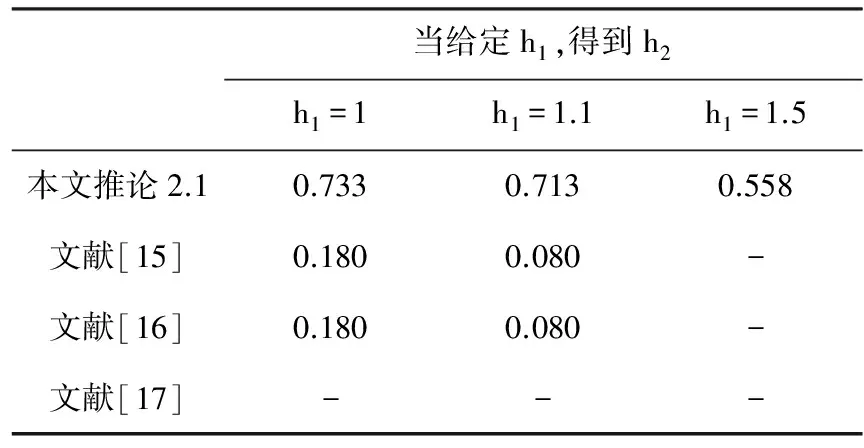
4 結束語


