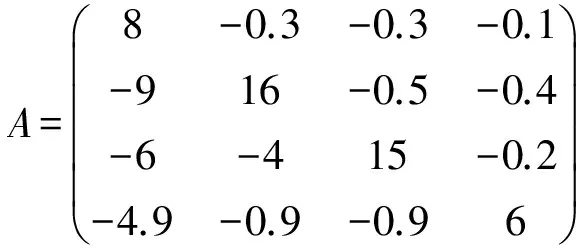Nekrasov矩陣的逆矩陣無窮范數(shù)上界的進一步研究
李艷艷
(文山學(xué)院 數(shù)學(xué)學(xué)院, 云南 文山 663009)
Nekrasov矩陣的逆矩陣無窮范數(shù)上界的進一步研究
李艷艷
(文山學(xué)院 數(shù)學(xué)學(xué)院, 云南 文山 663009)
通過引入恰當(dāng)?shù)膮?shù),構(gòu)造嚴(yán)格對角占優(yōu)矩陣,并利用該矩陣與Nekrasov矩陣的關(guān)系,得到Nekrasov矩陣的逆矩陣無窮范數(shù)的帶有參數(shù)的2個新上界.數(shù)值算例說明:一定情況下,得到的新上界提高了現(xiàn)有的結(jié)果,從而對現(xiàn)有文獻進行了有益補充.
Nekrasov矩陣; H矩陣; 無窮范數(shù); 逆矩陣; 上界
H矩陣被廣泛應(yīng)用于眾多領(lǐng)域[1],它的許多子類都得到了大量學(xué)者的研究[2-14],但是Nekrasov矩陣作為H矩陣的重要子類,關(guān)于它的研究主要集中在矩陣的判定、特征值的估計等方面[5-8].本文研究目前較少探討但很有意義的該類矩陣的逆矩陣無窮范數(shù)的上界問題.
1 預(yù)備知識
令Cn×n(Rn×n)表示復(fù)(實)矩陣的集合,N表示自然數(shù)的集合.
設(shè)A=(aij)∈Rn×n,若A的比較矩陣
可逆,且〈A〉-1≥0,則稱〈A〉是M矩陣,同時稱A是H矩陣.
設(shè)A=(aij)∈Rn×n,若
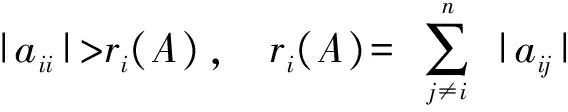
則稱A是嚴(yán)格對角占優(yōu)矩陣;若
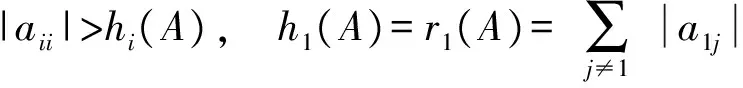
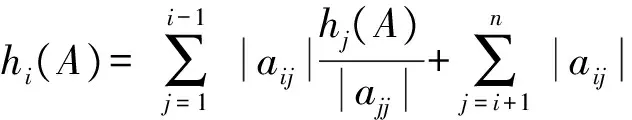
i=2,3,…,n,
則稱A是Nekrasov矩陣.
為了后面研究的需要,將矩陣A分裂為
A=D-L-U,
其中
D=diag(a11,a22,…,ann),

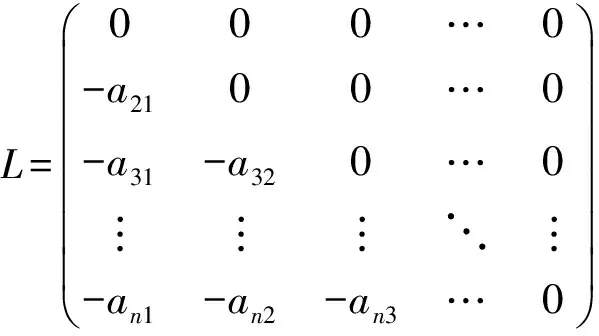
引理 1[9]設(shè)A=(aij)∈Rn×n是非奇異H矩陣,則
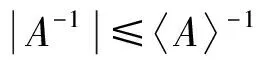
引理 2[10]設(shè)
A=(aij)∈Rn×n,n≥2,aii≠0,
則
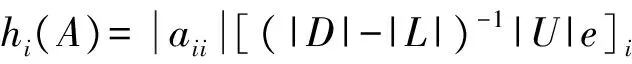
e=(1,1,…,1).
引理 3[11]矩陣A=(aij)∈Rn×n,n≥2是Nekrasov矩陣的充要條件是
(|D|-|L|)-1|U|e 同時,該條件還隱含了E-(|D|-|L|)-1|U|是嚴(yán)格對角占優(yōu)矩陣,其中E是單位矩陣. 引理 4[12]設(shè)A,B∈Rn×n,A、A-B是非奇異矩陣,則 (A-B)-1=A-1+A-1B(E-A-1B)-1A-1. 引理 5[12]若‖A‖<1,那么E-A是非奇異的,且 ‖(E-A)-1‖. 下面通過引入恰當(dāng)?shù)膮?shù),構(gòu)造嚴(yán)格對角占優(yōu)矩陣,并利用該矩陣與Nekrasov矩陣的關(guān)系,得到Nekrasov矩陣的逆矩陣無窮范數(shù)的帶有參數(shù)的2個新上界. 定理 1 設(shè)矩陣A=(aij)∈Rn×n是Nekrasov矩陣,若 則 ‖A-1‖ 其中 z1(A)=1, 證明 令 C=E-(|D|-|L|)-1|U|, 由于矩陣A是Nekrasov矩陣,由引理3知,C是嚴(yán)格對角占優(yōu)矩陣,再令 C(μ)=CD(μ)=(E-(|D|-|L|)-1|U|)D(μ), 其中 由文獻[13]中的引理4知C(μ)也是嚴(yán)格對角占優(yōu)矩陣.進一步 C(μ)=(|D|-|L|)-1〈A〉D(μ), 那么 〈A〉=(|D|-|L|)C(μ)D(μ)-1, 即 ‖〈A〉-1‖≤ ‖D(μ)‖‖C(μ)-1‖‖(|D|-|L|)-1‖. 又由引理1知 ‖A-1‖≤‖〈A〉-1‖, 所以 ‖A-1‖≤‖〈A〉-1‖≤ ‖D(μ)‖‖C(μ)-1‖‖(|D|-|L|)-1‖. 為了得到‖A-1‖的上界,分別研究‖C(μ)-1‖和‖(|D|-|L|)-1‖的界. 首先,研究‖(|D|-|L|)-1‖的界.因為|D|-|L|是M矩陣,則 ‖(|D|-|L|)-1‖=‖(|D|-|L|)-1e‖, 令 y=(|D|-|L|)-1e, 則 e=(|D|-|L|)y. 寫成分量有 ‖(|D|-|L|)-1‖=‖y‖. 其次,研究‖C(μ)-1‖的界.利用C(μ)的定義和引理4知 ‖C(μ)-1‖= ‖[(E-(|D|-|L|)-1|U|)D(μ)]-1‖≤ ‖(E-(|D|-|L|)-1|U|)-1‖‖D(μ)-1‖= ‖E+E-1(|D|-|L|)-1|U|(E-E-1(|D|- |L|)-1|U|)-1E-1‖‖D(μ)-1‖≤ ‖E‖+‖E‖‖(|D|-|L|)-1‖‖|U|‖× (1) 將 ‖(|D|-|L|)-1‖=‖y‖, 代入(1)式有 ‖C(μ)-1‖. 結(jié)合以上得 ‖A-1‖≤‖〈A〉-1‖≤ ‖D(μ)‖‖C(μ)-1‖‖(|D|-|L|)-1‖= ‖D(μ)‖‖D(μ)-1‖ 關(guān)于μ的取值,分類討論如下: 當(dāng)μ>1時有 ‖A-1‖, 當(dāng)μ<1時有 ‖A-1‖; 即 ‖A-1‖ 定理證畢. 定理 2 設(shè)矩陣A=(aij)∈Rn×n是Nekrasov矩陣,若 則 ‖A-1‖ 其中 z1(A)=1, 證明 設(shè)B=|D|C,由于矩陣A是Nekrasov矩陣,則由引理3知E-(|D|-|L|)-1|U|,B是嚴(yán)格對角占優(yōu)矩陣.再令 B(μ)=BD(μ)= 即 ‖A-1‖≤‖〈A〉-1‖≤ ‖D(μ)‖‖B(μ)-1‖‖(E-|L||D|-1)-1‖. 為了得到‖A-1‖的上界,分別研究‖(E-|L||D|-1)-1‖和‖B(μ)-1‖的界. 首先研究‖(E-|L||D|-1)-1‖的界.由于E-|L||D|-1是M矩陣,則 定義 則 寫成分量形式有 z1(A)=1, 則 其次研究‖B(μ)-1‖的上界.由B(μ)的定義知 ‖B(μ)-1‖≤‖|D|-1‖× 而 ‖(E-(|D|-|L|)-1|U|)-1‖= ‖E+E-1(|D|-|L|)-1|U|(E- E-1(|D|-|L|)-1|U|)-1E-1‖= ‖E+E(|D|-|L|)-1|U|(E- E(|D|-|L|)-1|U|)-1‖≤ ‖E‖+‖E‖‖(|D|-|L|)-1‖× ‖|U|‖ 1+‖(|D|-|L|)-1‖‖|U|‖× 所以 ‖B(μ)-1‖≤ ‖|D|-1‖ ‖D(μ)-1‖. 由以上關(guān)系得 ‖A-1‖≤‖〈A〉-1‖≤ ‖D(μ)‖‖B(μ)-1‖‖(E-|L||D|-1)-1‖≤ 下面關(guān)于μ的取值進行如下討論: 當(dāng)μ>1時有 ‖〈A〉-1‖, 當(dāng)0<μ<1時有 ‖〈A〉-1‖ 則 ‖A-1‖ 綜上所述,定理得證. 且由定義知A是Nekrasov矩陣,應(yīng)用文獻[13]中的估計式得‖A-1‖≤0.402 3,應(yīng)用文獻[14]中的估計式得‖A-1‖≤0.445 3;應(yīng)用本文的結(jié)果,當(dāng)μ=0.98時得 ‖A-1‖≤0.397 6, ‖A-1‖≤0.389 1, 而其真值為‖A-1‖=0.330 8. 該數(shù)值算例說明,本文的估計式改進了現(xiàn)有的結(jié)果. 致謝 文山學(xué)院科學(xué)研究項目(16WSY11)對本文給予了資助,謹(jǐn)致謝意. [1] CVETKOVIC L.Hmatrix theory vs Eigenvalue localication[J]. Num Algor,2006,42:229-245. [2] 高美平.M矩陣與其逆的Hadamard積的最小特征值的下界新的估計式[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2014,37(1):90-97. [3] 李艷艷,李耀堂,蔣建新. 嚴(yán)格對角占優(yōu)M矩陣A的‖A-1‖上界估計式的改進[J]. 云南大學(xué)學(xué)報(自然科學(xué)版),2015,37(1):5-8. [4] 李瑩,呂智超,查秀秀,等. 矩陣的特殊結(jié)構(gòu)最小范數(shù)廣義逆[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2015,38(5):678-681. [5] LI W. On Nekrasov matrices[J]. Linear Algebra and Its Application,1998,281(1):87-96. [6] 郭愛麗,聶祥榮,武玲玲. Nekrasov矩陣行列式界的估計[J]. 安徽大學(xué)學(xué)報(自然科學(xué)版),2015,39(6):15-18. [7] 王銀燕,徐伸,陸全. 廣義Nekrasov矩陣的迭代判定準(zhǔn)則[J]. 高等學(xué)校計算數(shù)學(xué)學(xué)報,2015,37(1):19-30. [8] 郭愛麗,劉建州. 廣義Nekrasov矩陣的新判據(jù)[J]. 數(shù)學(xué)的實踐與認(rèn)識,2016,46(5):239-245. [9] BERMAN A, PLEMMONS R J. Nonnegative matrices in the mathematical sciences[C]//Classics in Applied Mathematics. New York:Academic Press,1979. [10] ROBERT F. BlocsHmatrices et convergence des methods iteratives classiques par blocs[J]. Linear Algebra and Its Application,1969,2(2):223-265. [11] SZULC T. Some remarks on a theorem of Gudkov[J]. Linear Algebra and Its Application,1995,225(225):221-235. [12] 趙建興,桑彩麗. 嚴(yán)格α-對角占優(yōu)M矩陣A的‖A-1‖的上界估計[J]. 數(shù)學(xué)的實踐與認(rèn)識,2015,45(19):280-284. [13] LI C Q , PEI H, GAO A, et al. Improvements on the infinity norm bound for the inverse of Nekrasov matrices[J]. Numerical Algorithms,2016,71(3):613-630. 2010 MSC:15A15; 15A57 (編輯 余 毅) Further Study on the Upper Bound of the Infinity Norm for the Inverse Matrix of the Nekrasov Matrix LI Yanyan (CollegeofMathematics,WenshanCollege,Wenshan663009,Yunnan) By introducing the appropriate parameters, we construct the strictly diagonally dominant matrix. Further, by the relationship between the matrix and the Nekrasov matrix, two new upper bounds of the infinity norm of the inverse matrix of the Nekrasov matrix are obtained. Numerical example explain that, under certain circumstances, some of the existing results in the new territories have been raised, so this is a useful supplement to the existing literature. Nekrasov matrices;Hmatrices; infinity norm; inverse matrices; upper bounds 2016-09-05 國家自然科學(xué)基金(11261049)和云南省科技廳應(yīng)用基礎(chǔ)研究項目(2013FD052) 李艷艷(1982—),女,講師,主要從事矩陣?yán)碚摷捌鋺?yīng)用的研究,E-mail:529374583@qq.com. O151.21 A 1001-8395(2017)04-0491-05 10.3969/j.issn.1001-8395.2017.04.0112 Nekrasov矩陣無窮范數(shù)的上界
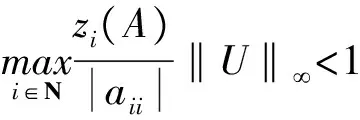
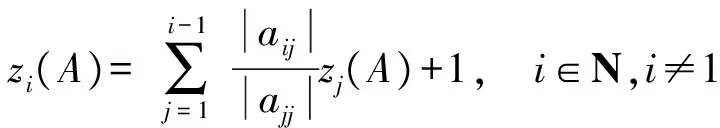
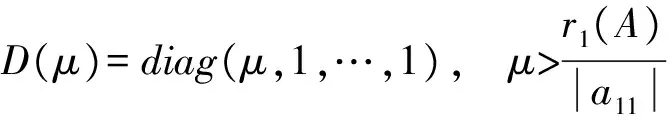
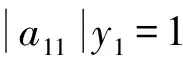
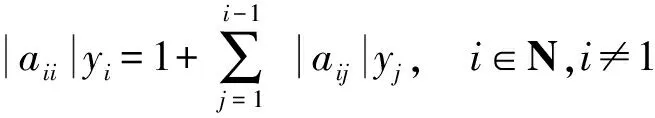
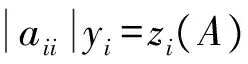
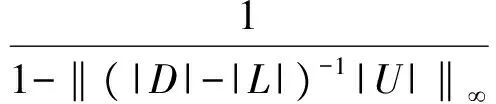
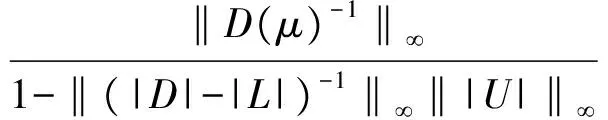
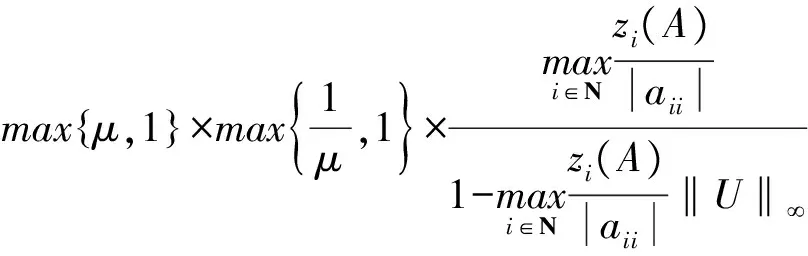
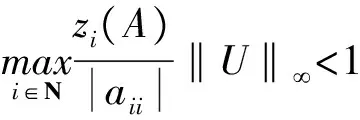
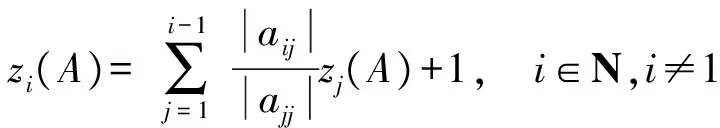
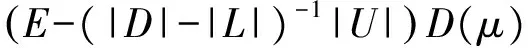
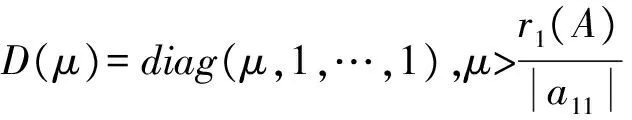
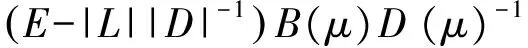
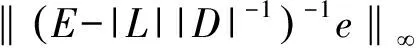
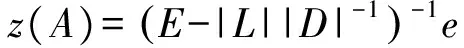
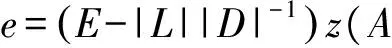
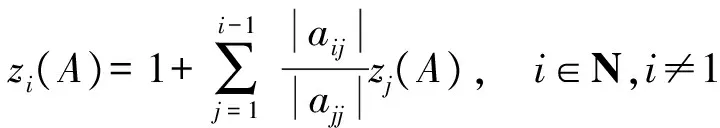
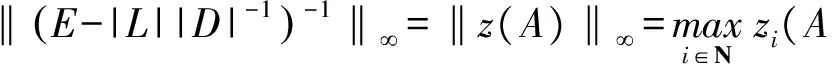
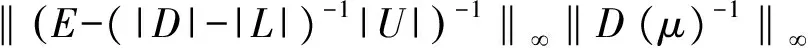
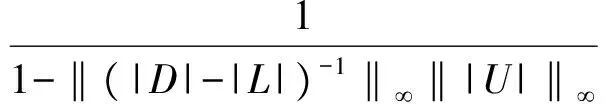
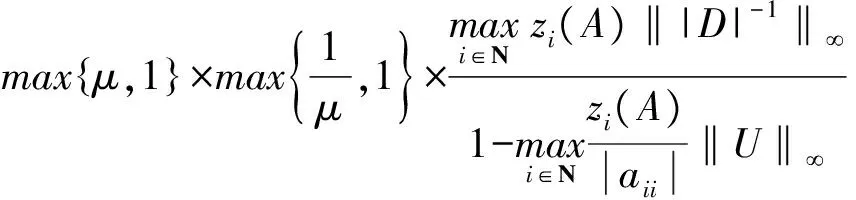
3 數(shù)值算例