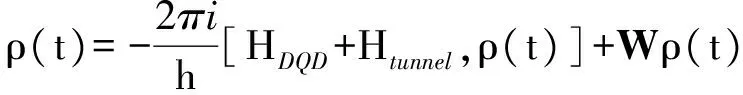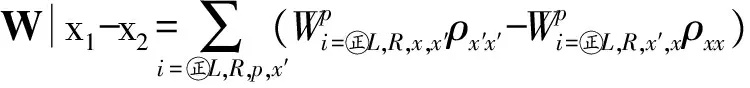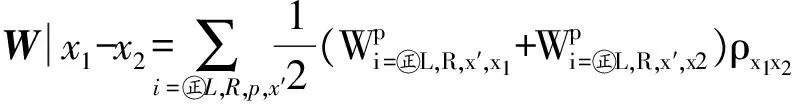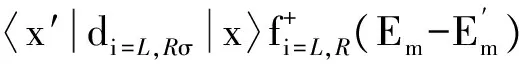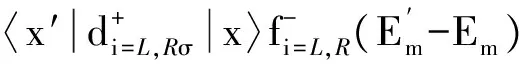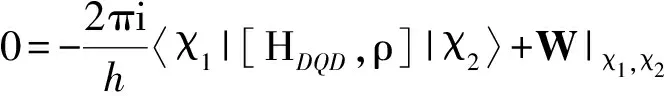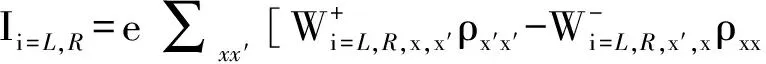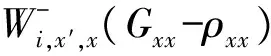馬約拉納費米子-量子點雜化系統輸運性質的研究

毛 祥, 吳紹全

(四川師范大學 物理與電子工程學院， 四川 成都 610101)

馬約拉納費米子-量子點雜化系統輸運性質的研究

毛 祥, 吳紹全*

(四川師范大學 物理與電子工程學院， 四川 成都 610101)

從理論上研究馬約拉納費米子-量子點雜化系統的輸運性質.基于廣義主方程方法,計算通過此系統的電流、微分電導和Fano因子.計算結果表明:馬約拉納費米子與量子點中電子的耦合導致系統的零偏置反常,而2個馬約拉納費米子的耦合壓制系統的零偏置反常.

馬約拉納費米子； 零偏置反常； 主方程方法； 微分電導； Fano因子

在最近幾年，針對拓撲超導體的研究已經成為凝聚態物理中非常熱門的課題[1-4],其主要原因之一是理論研究表明拓撲超導體中的含有馬約拉納費米子.馬約拉納費米子滿足非阿貝爾交換統計[5-9],其主要特征就是它的反粒子是它自己本身,即如果γ為馬約拉納費米子的消滅算子,則有γ=γ+,這使得該粒子不受退相干的影響,這在拓撲量子計算機中有重要的潛在應用價值[10-11].此外,在分數量子霍爾系統、P-波超導體半量子渦旋、摻雜拓撲絕緣體中超導渦旋的兩端等都存在馬約拉納費米子.目前,大量的理論研究已經提出了如何在實驗室中實現拓撲超導體[12-23],許多探測馬約拉納費米子的儀器已在實驗室中制造出來了,并已初步探測到了馬約拉納費米子存在的信息[24-32].在這些信息中,最為引人關注的一個實驗探測是把一根半導體量子線與一個超導體接觸,由于近鄰效應,這根半導體量子線帶有超導性；再把它與一根金屬線組成一個雜化系統,在這個系統中探測到了一個電導的零偏置常峰作為馬約拉納費米子存在的證據[24-26].

拓撲量子計算機的主要優點是不受退相干的影響,且計算的基礎是由成對的馬約拉納費米子構成.每對馬約拉納費米子在空間中都是分離的,每個馬約拉納費米子只與另一個馬約拉納費米子耦合成對,由此形成一個費米能級，能級的占據數可以編碼為一個量子比特，這種非局域的拓撲量子比特不受局域的微擾的影響.然而基于同樣的原因，要轉移和讀出拓撲態的信息同樣是一個大的挑戰.現在已經有人建議用馬約拉納費米子-量子點雜化系統作為解決這個問題的途徑之一[33].各種不同的馬約拉納費米子-量子點雜化系統[26-33]被提出來的目的是探測馬約拉納費米子、調整非局域關聯、估計壽命、消除無序的影響.因此，研究馬約拉納費米子-量子點雜化系統的輸運性質是重要的.

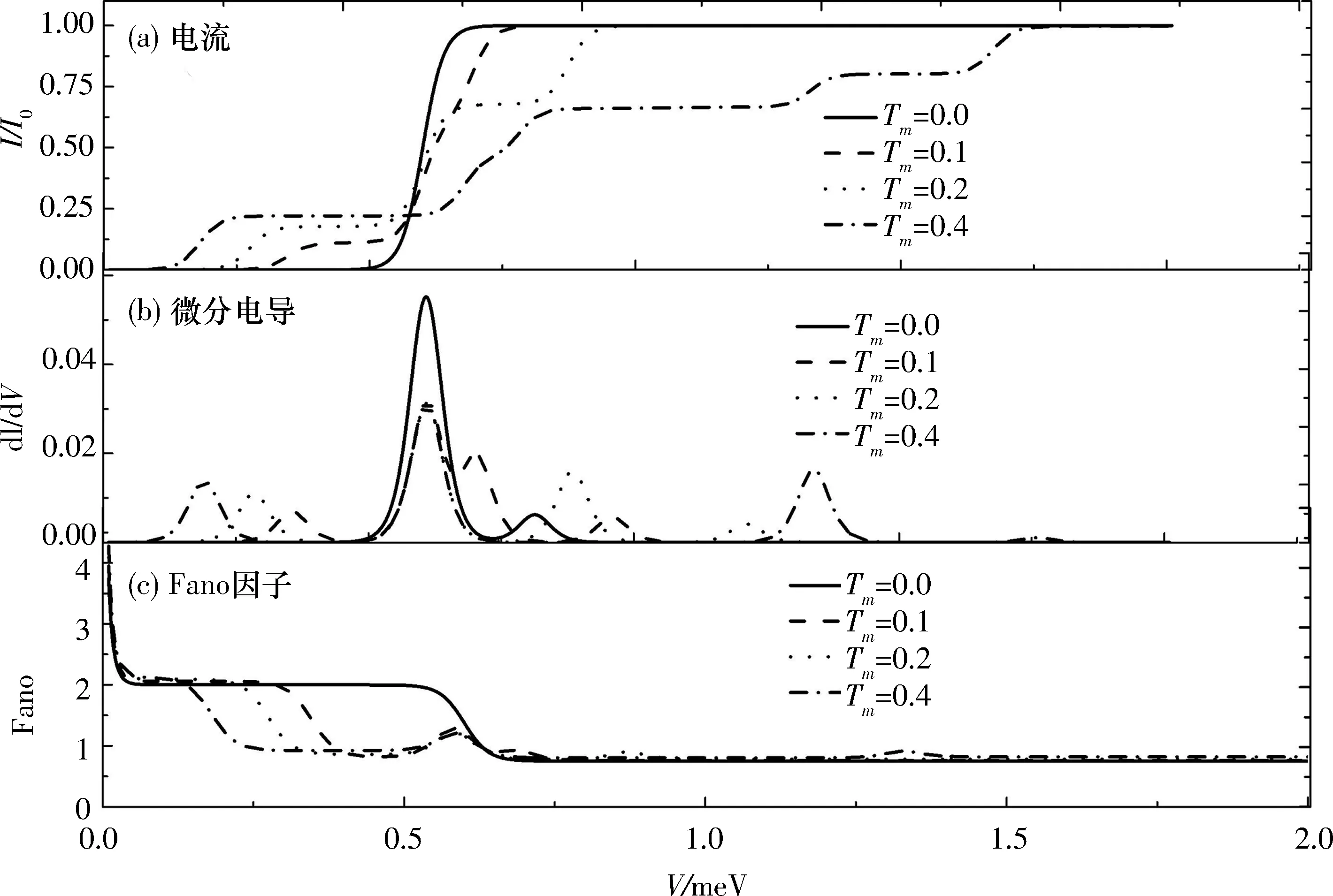
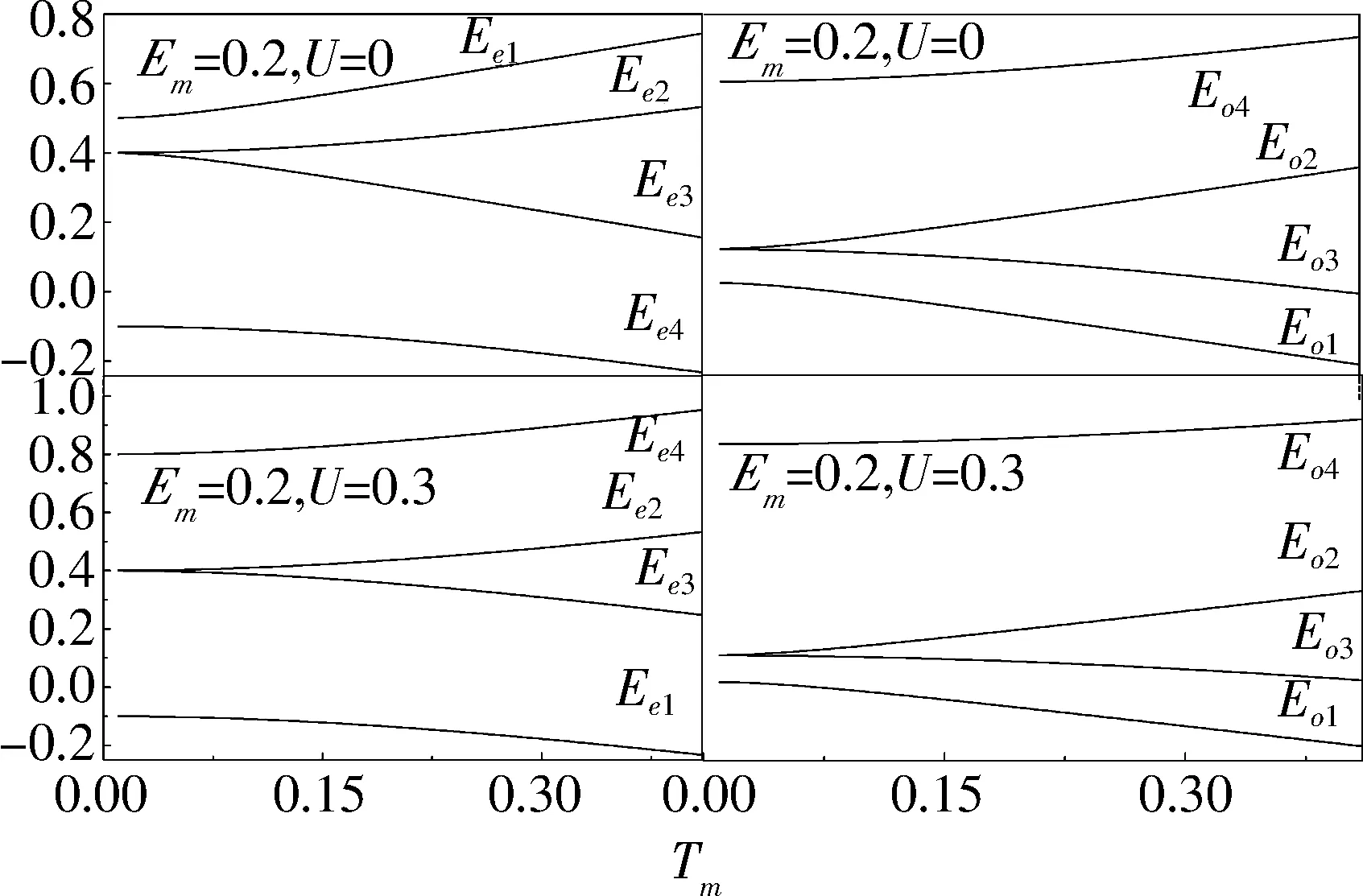
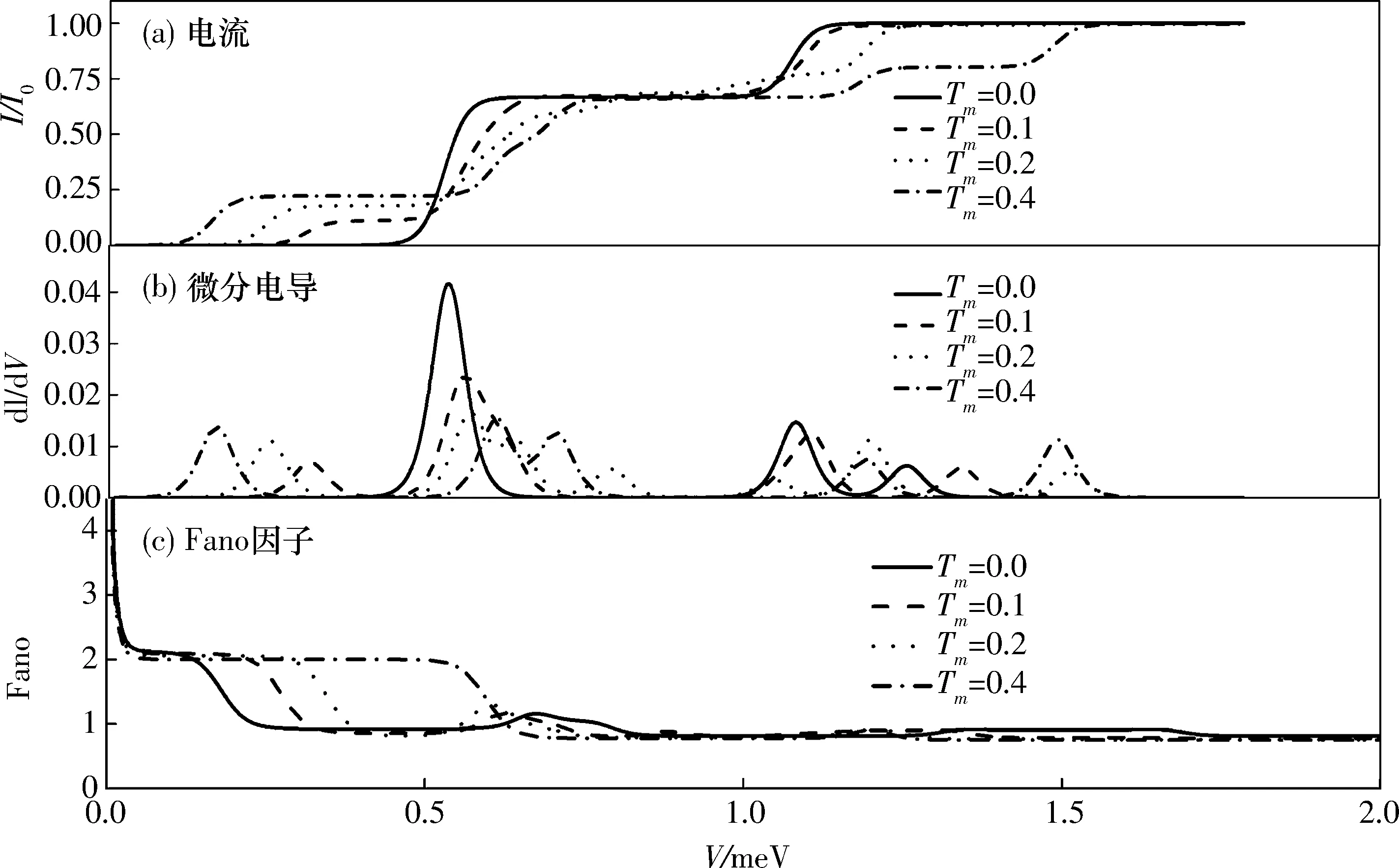
本文基于廣義主方程方法研究了馬約拉納費米子-量子點雜化系統的輸運性質，研究結果表明：馬約拉納費米子與量子點中電子的耦合Tm消除了系統的四重簡并，但維持了系統4個雙重簡并，而雙重簡并的基態隨偏壓的增加而負增長，由此導致系統的零偏置反常；庫侖相互作用僅僅增加了系統量子態|e4〉和|o4〉的能量,因而增加了電流臺階,但庫侖相互作用不會改變系統量子態的簡并度,也不會壓制零偏置反常現象.而2個馬約拉納費米子的耦合壓制了系統的零偏置反常,并消除了基態和最高能態的雙重簡并，但維持了2個中間能態的簡并.

本文所研究的系統(系統模型如圖1)可用一個與馬約拉納費米子相耦合的單量子點安德森模型描述[33-34].哈密頓量H=Hlead+HQD+Htunnel,3個分量分別為:

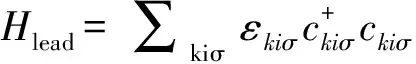
圖 1 系統模型

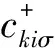
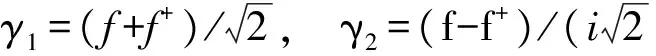
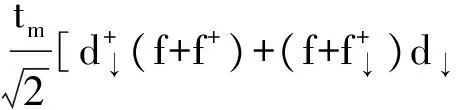
Htunnel是導體與量子點之間的隧穿耦合，其耦合強度可以用其固有線性寬度來表示，用公式可表示成Γiσ=2π|ti|2ρiσ,，ti指的是量子點與左右兩端導體的隧穿矩陣元，而ρiσ指的是對應導體中的電子態密度.

在主方程近似下,與馬約拉納費米子耦合的單量子點系統共有8個量子態，分別為：|0,0〉、|↑,0〉、|↓,0〉、|0,1〉、|↑,1〉、|↓,1〉、|↑↓,0〉、|↑↓,1〉；但這8個量子態不是HQD的本征態,通過久期方程,可以得到該哈密頓量的本征值和本征能量如表1所示.

表 1 系統本征態和能量

表1中各式的參數為：

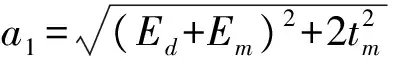
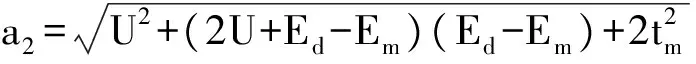
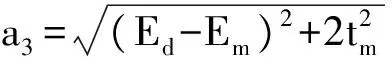
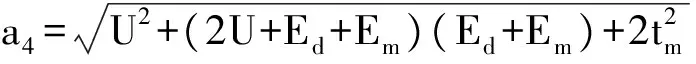
b1=-(Ed+Em+a1)， b2=-(Ed+Em-a1)，

b3=-(Ed-Em+U+a2)， b4=-(Ed-Em+U-a2)，

b5=-(Em-Ed+a3)， b6=-(Em-Ed-a3)，

b7=-(Ed+Em+U+a4)， b8=-(Ed+Em+U-a4)，

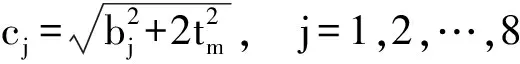
Ee1=(Ed-a1)/2, Ee2=(Ed+a1)/2,

Ee3=(3Ed+U-a2)/2, Ee4=(3Ed+U+a2)/2,

Eo1=(Ed-a3)/2, Eo2=(Ed+a3)/2,

Eo3=(3Ed+U-a4)/2, Eo4=(3Ed+U+a4)/2.

本文主要研究量子點與電極處于弱耦合時的輸運性質，選擇Γiσ

(2)

其中W是一個矩陣,與隧穿進程相關.約化密度算子在系統量子態中的矩陣元ρx1x2=〈x1|ρ|x2〉,其中x1和x2是雙量子點系統的本征態.當x1=x2=x時,密度矩陣的對角元ρx1x2代表了雙量子點系統處于x態的概率,所表征的意思是在量子點系統中可以探測到量子態x出現的幾率的大小.

(3a)

在方程3(a)和3(b)中,p=+、-描述了在電子躍遷時電子的流向,+表示電子流向為流入量子點,-表示電子流向為流出量子點.當量子態通過正交化處理后,矩陣W只包含對角元,

(4a)

在定態的情況下,系統各個占有態出現的幾率是穩定的,滿足一般主方程

(5)

通過使用歸一化條件,求解8個方程組成的線性齊次方程組,可得到約化密度矩陣的各個矩陣元.將約化密度矩陣元素代入(6)式便可得到通過系統的電流

(6)其微分電導由di=dIi/dU計算.此外，電流實際上是由大量單個電子單獨作用的總結果,而每個電子

可以認為是隨機獨立出現的,所以電子形成的電流并不是固定不變的，而是在一個平均值上起伏變化，散粒噪聲就是反映電流這種起伏變化大小的量，因此散粒噪聲可以為提供電流所不能提供的有關電子輸運的額外信息.計算散粒噪聲[36]的標準公式為

(7)

在主方程近似下，零頻散粒噪聲[32-33]的計算公式可表示為

(8)

ρxx〈x′|-Ii|x〉ρx′x′〈x|]=0.

(9)

計算中一些具體參數取值：T=0.01,ΓL=ΓR=Γ0=0.005,Ed=0.3,和I0=2πeΓ0/h,所有參數都以Γ0作為能量單位.

首先討論Em=0,U=0的情況,圖2展示了通過量子點的電流、微分電導和Fano因子隨偏壓變化的情況，而圖3展示了量子態能量隨Tm變化的情況.

圖 2 在Em=0和U=0時，通過系統的電流、微分電導和Fano因子隨電壓的變化曲線

圖 3 系統各量子態的能量隨Tm變化的曲線

當Tm=0的時候，從圖2中可以發現，在U<2Ed時，由于偏壓沒有達到閾值電壓，量子點是空的和電流被阻塞.隨著偏壓的增加接近閾值電壓時，系統的量子態開始由態|e1〉和|o1〉向態|e2〉、|e3〉、|e4〉、|o2〉、|o3〉和|o4〉躍遷，使得通過系統的序貫電流開始單調地增加，并最終到達一個平臺,并在U=2Ed=0.6 V處,其微分電導的變化曲線上出現的一個波峰.在U<2Ed時，Fano因子大于1，這種超泊松噪聲的現象是由于偏壓小于閾值電壓，電子的隧穿受到壓制所致;當U

漲落導致Fano因子開始趨于發散;而在U>2Ed時，Fano因子小于1(泊松噪聲)但大于0.5(雙勢壘噪聲).從圖3的能級圖可以看到，此時量子態|e1〉與|o1〉和量子態|o3〉與|o4〉為二重簡并,而|e2〉、|e3〉、|o2〉和|o3〉為四重簡并.當Tm≠0時,情況起了變化,原來四重簡并的量子態|e2〉、|e3〉、|o2〉和|o3〉分裂成了|e2〉與|o2〉和|e3〉與|o3〉的二重簡并,Ee2和Eo2與Ee4和Eo4一樣，其值隨Tm的增加而增加;但Ee3和Eo3隨Tm的增加而減少，這導致電流線型呈現出多臺階.尤其值得注意的是，Ee1和Eo1隨Tm的增加而負增長，這導致在偏壓為零時電子隧穿就開始出現了，這就是著名的零偏置反常現象.微分電導在電流線型中每個臺階處都出現了一個波峰，而Fano因子在U<2Ed時等于1，為泊松噪聲，并在U=0.6 V處出現了一個峰值大于1的波峰，這是由于在偏壓達到閾值電壓時打開了一個新的電子隧穿通道,導致電流有大的漲落.從圖3還可以看到，隨著偏壓的增加，每打開一個電子隧穿通道都會導致Fano因子出現一個波峰.在Tm的增加過程中,整個系統保持偶宇稱量子態與奇宇稱量子態一對一的雙重簡并,既Tm的出現消除了系統的四重簡并,但保持了系統的雙重簡并,導致零偏置反常現象的出現.

圖 4 在Em=0和U=0.3 V時，通過系統的電流、微分電導和Fano因子隨電壓的變化曲線

圖4展示了當Em=0,U=0.3 V時通過量子點的電流、微分電導和Fano因子隨偏壓變化的情況.可以看到,在Tm=0時,庫侖相互作用增加了量子態|e4〉和|o4〉的能量,也就增加了量子點通過這2個量子態隧穿的閾值電壓,導致電流線型呈現出2個臺階,分別對應2個閾值電壓U=0.6和1.2 V,伴隨每個電流臺階的出現都會在微分電導和Fano因子線型中留下一個波峰,標志著電子隧穿通道的打開所引起電流的漲落.與圖2一樣,隨著Tm的出現,不僅導致零偏置反常現象,也使四重簡并量子態|e2〉、|e3〉、|o2〉和|o3〉的退化為二重簡并,使得電流線型最后呈現出4個臺階,伴隨電流線型中每個臺階處的出現都會導致在微分電導和Fano因子線型中出現一個波峰,所以庫侖相互作用僅僅增加了量子態|e4〉和|o4〉的能量,因而增加了電流臺階,但庫侖相互作用不會影響系統量子態的簡并度,也不會壓制零偏置反常現象.

圖 5 在Em=0.2和U=0時，通過系統的電流、微分電導和Fano因子隨電壓的變化曲線

在Em=0.2,U=0時,圖5展示了通過量子點的電流、微分電導及Fano因子隨偏壓變化的情況，而圖6展示了量子態能量隨Tm變化的情況.從圖5中可以看到:原來二重簡并的量子態|e1〉與|o1〉和|o3〉與|o4〉分裂了,而原來四重簡并的量子態|e2〉、|e3〉、|o2〉和|o3〉分裂為|e2〉與|e3〉和|o2〉與|o3〉的二重簡并,如此系統形成了4個激發態.特別是分裂后的量子態|e1〉的能量小于零,而量子態|o1〉的能量大于零,Em導致系統量子態能級的這種分裂顯著地改變了系統的輸運性質.首先討論Tm=0的情況.從圖6中可以清楚地看到:電流、微分電導和Fano因子隨偏壓變化的情況與Em=0和U=0時的情況是一樣的,這說明單獨Em的出

圖 6 系統各量子態的能量隨Tm變化的曲線

Fig. 6 The eigenenergies of quantum states of the system as a function ofTm

現不會影響量子點的輸運性質.這很好理解,因為這時量子點與P-波超導體退藕.然而當Tm≠0的時候情況有了很大地不同.隨Tm的增加,由于Em消除了系統的能級簡并,形成了4個激發態,出現了4個閾值電壓,控制著4個電子隧穿通道,隨著偏壓的增加,4個電子隧穿通道依次被打開,最后導致電流線型隨偏壓的變化出現了4個臺階,每個臺階的出現都會在微分電導和Fano因子的線型中留下一個波峰.特別是由于Em消除了基態能級Ee1和Eo1的簡并,并且Ee1<0而Eo1>0,這導致零偏置反常消失了.此外在偏壓小于閾值電壓的阻塞區,Fano因子大于1,系統出現由于電子隧穿受到阻塞而導致的超泊松噪聲現象,一旦打開一個電子隧穿通道,Fano因子迅速降為一,系統進入泊松噪聲.這點與Em=0似的情況不一樣,在那里由于Tm≠0時系統出現零偏置反常,所以一旦Tm≠0,Fano因子迅速降為一,系統進入泊松噪聲.

圖7展示了在Em=0.2,U=0.3 V時,通過量子點的電流、微分電導及Fano因子隨偏壓變化的情況，此時的情況與Em=0.2,U=0時稍有不同的是在Tm=0時,由于庫侖相互作用的出現,增加了雙占據態的能量,導致電流線型隨偏壓的變化出現了2個臺階.但隨著Tm的增加,其能級分裂情況與在Em=0.2,U=0時能級分裂情況是一樣的,電流線型隨偏壓的變化最后演變出了4個臺階,而微分電導和Fano因子隨偏壓變化的線型在2種取值條件下也是一樣的,這說明當Em和Tm都不為零時,庫侖相互作用U對量子點輸運性質沒有影響.

圖 7 在Em=0.2和U=0.3 V時，通過系統的電流、微分電導和Fano因子隨電壓的變化曲線

本文研究了馬約拉納費米子-量子點雜化系統的輸運性質，研究結果表明:馬約拉納費米子與量子點中電子的耦合Tm導致了系統的零偏置反常，并消除了系統的四重簡并,使系統變成了4個雙重簡并.庫侖相互作用僅僅增加了系統量子態|e4〉和|o4〉的能量,因而增加了電流臺階,但庫侖相互作用不會改變系統量子態的簡并度,也不會壓制零偏置反常現象.而2個馬約拉納費米子的耦合壓制了系統的零偏置反常,并消除了基態和最高能態的雙重簡并，但維持了2個中間能態的簡并.該系統的這些性質在量子器件開發和拓撲量子計算開發等方面有重要的意義.

[1] EUGENIE S R. A solid case for Majorana fermions[J]. Nature,2012,483(7388):132.

[2] BROUWER P W. Enter the Majorana fermion[J]. Science,2012,336(6084):989-990.

[3] WILCZEK F. Quantum physics:Majorana modes materialize[J]. Nature,2012,486(7402):195-197.

[4] ALICEA J. New directions in the pursuit of Majorana fermions in solid state systems[J]. Reports on Progress in Physics Physical Society,2012,75(7):076501.

[5] 郭雪林,黃勁松,謝征微,等. FM/I/FM隧道結中的隧穿時間[J]. 四川師范大學學報(自然科學版),2009,32(2):202-205.

[6] READ M N. Nonabelions in the fractional quantum Hall effect[J]. Nuclear Physics,1991,B360(2/3):362-396.

[7] NAYAK C, WILCZEK F. 2n-quasihole states realize 2n-1-dimensional spinor braiding statistics in paired quantum Hall states[J].Nuclear Physics,1996,B479(3):529-553.

[8] 陳尚榮,徐明,劉杰. 鐵磁體/有機體/鐵磁體三明治結構的隧穿磁電阻[J] . 四川師范大學學報(自然科學版),2009,32(4):482-485.

[9] READ N, GREEN D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect[J]. Phys Rev,2000,B61:10267.

[10] KITAEV A Y. Fault-tolerant quantum computation by anyons[J]. Ann Phys,2003,303(1):2-30.

[11] NAYAK C, SIMON S H, Stern A, et al. Non-Abelian anyons and topological quantum computation[J]. Rev Mod Phys,2008,80:1083.

[12] FU L, KANE C L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator[J]. Phys Rev Lett,2008,100(9):096407.

[13] 侯濤,吳紹全,畢愛華. 耦合于鐵磁電極平行雙量子點的自旋極化輸運[J]. 四川師范大學學報(自然科學版),2009,32(2):210-214.

[14] FU L, KANE C L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction[J]. Phys Rev,2009,B79:161408.

[15] SAU J D, LUTCHYN R M, TEWARI S, et al. Generic new platform for topological quantum computation using semiconductor heterostructures[J]. Phys Rev Lett,2010,104(4):040502.

[16] ALICEA J. Majorana fermions in a tunable semiconductor device[J]. Phys Rev,2010,B81:125318.

[17] 李玲,高潔. 單電子輸運器件及其研究進展[J]. 四川師范大學學報(自然科學版),2009,32(6):822-833.

[18] LUTCHYN R M, SAU J D, SARMA S D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures[J]. Phys Rev Lett,2010,105(7):077001.

[19] OREG Y, REFAEL G, VON OPPEN F. Helical liquids and Majorana bound states in quantum wires[J]. Phys Rev Lett,2010,105(17):177002.

[20] COOK A, FRANZ M. Majorana fermions in a topological-insulator nanowire proximity-coupled to an s-wave superconductor[J]. Phys Rev,2011,B84:201105.

[21] 徐明,魏屹,何賢模,等. Si/SiNx多層膜能帶結構的理論研究[J]. 四川師范大學學報(自然科學版),2010,33(4):545-548.

[22] SAU J D, SARMA S D. Realizing a robust practical Majorana chain in a quantum-dot-superconductor linear array[J]. Nature Commun,2012,3(1):964.

[23] NADJPERGE S, DROZDOV I K, BERNEVIG B A, et al. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor[J]. Phys Rev,2013,B88:020407.

[24] MOURIK V, ZUO K, FROLOV S M, et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices[J]. Science,2012,336 (6084):1003.

[25] DAS A, RONEN Y, MOST Y, et al. Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions[J]. Nature Phys,2012,8(12):887-895.

[26] DENG M T, YU C L, HUANG G Y, et al. Anomalous zero-bias conductance peak in a Nb-InSb nanowire-Nb hybrid device[J]. Nano Lett,2012,12(12):6414-6419.

[27] FINCK A D K, VAN HARLINGEN D J, MOHSENI P K, et al. Anomalous modulation of a zero-bias peak in a hybrid nanowire-superconductor device[J]. Phys Rev Lett,2013,110:126406.

[28] CHURCHILL H O H, FATEMI V, GROVE-RASMUSSEN K, et al. Superconductor-nanowire devices from tunneling to the multichannel regime:Zero-bias oscillations and magnetoconductance crossover[J]. Phys Rev,2013,B87:241401.

[29] NADJPERGE S, DROZDOV I K, LI J, et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor[J]. Science,2014,346(6209):602-607.

[30] DENG M T, YU C L, HUANG G Y, et al. Parity independence of the zero-bias conductance peak in a nanowire based topological superconductor-quantum dot hybrid device[J]. Sci Rep,2013,4(7621):7261-7261.

[31] HIGGINBOTHAM A P, ALBRECHT S M, KIRSANSKAS G, et al. Parity lifetime of bound states in a proximitized semiconductor nanowire[J]. Nature Phys,2015,11(12):1017-1021.

[32] ALBRECHT S M, HIGGINBOTHAM A P, MADSEN M, et al. Exponential protection of zero modes in Majorana islands[J]. Nature,2016,531(7593):206-209.

[33] LEIJNSE M, FLENSBERG K. Quantum information transfer between topological and spin qubit systems[J]. Phys Rev Lett,2011,107(21):210502.

[34] LEE M, LIM J S, LPEZ R. Kondo effect in a quantum dot side-coupled to a topological superconductor[J]. Phys Rev,2013,B87:241402.

[35] BLUM K. Density Matrix Theory and Applications[M]. New York:Taylor & Francis,1996.

[36] BLANTER Y M, BüTTIKER M. Shot noise in mesoscopic conductors[J]. Physics Reports,2000,336(1/2):1-166.

(編輯 余 毅)

The Study of the Transport Properties of the Majorana Fermion-quantum Dot Hybrid System

MAO Xiang WU Shaoquan

(CollegeofPhysicsandElectronicEngineering,SichuanNormalUniversity,Chengdu610101,Sichuan)

We theoretically investigate the effect of the Majorana fermion on the transport properties through quantum dot hybrid system. With the framework of the generalized master equation method, we analyze the current through system, differential conductance and Fano factor as a function of bias. Our results reveal that the coupling of the Majorana fermion and electrons on the quantum dot can lead to a zero-bias anomaly, while the coupling of the two Majorana fermion inhibits the zero-bias anomaly, and relevant underlying physics problems is discussed.

the Majorana fermion; zero-bias anomaly; master equation method; differential conductance; Fano factor

2016-10-16

四川省教育廳自然科學重點科研基金(12ZA132)和四川省高校科研創新團隊建設計劃基金(12TD008)

O482.5

A

1001-8395(2017)04-0503-08

10.3969/j.issn.1001-8395.2017.04.013

*通信作者簡介： 吳紹全(1963—)，男，教授，主要從事介觀物理的研究，E-mail：2963434972@qq.com