不確定混沌系統的魯棒自適應容錯同步控制

鄧立為， 宋歌， 高俊山

(哈爾濱理工大學 自動化學院，黑龍江 哈爾濱 150080)

不確定混沌系統的魯棒自適應容錯同步控制

鄧立為， 宋歌， 高俊山

(哈爾濱理工大學 自動化學院，黑龍江 哈爾濱 150080)

針對一類帶有執行器故障、非線性不確定性以及外界干擾的混沌系統，設計一個魯棒自適應容錯控制器，來實現主從混沌系統之間的同步容錯控制。不需要知曉準確的故障信息以及外界干擾的上界，根據自適應律在線估計未知量。結合自適應控制技術，設計魯棒自適應容錯控制器，使得無論執行器是否有故障發生，主從兩個混沌系統都能夠實現同步。以經典的蔡氏混沌電路系統為例進行數值仿真，仿真結果驗證了所設計控制器的有效性和可行性。

自適應控制；容錯控制；混沌同步；執行器故障；外界干擾

0 引 言

混沌是一種復雜的非線性運動，由于混沌系統對初始條件和參數變化的極其敏感性和隨機性，使得混沌同步在保密通信、生物工程，信息處理等領域中得到廣泛的應用[1-3]。目前為止，學者們已經提出了許多有效的同步控制方法，例如線性與非線性反饋同步控制[4-5]、自適應同步控制[6]、滑模同步控制[7]、狀態觀測器控制[8]、模糊邏輯同步控制[9]等。文獻[10]針對帶有外部擾動和不確定性的混沌系統，設計一個魯棒滑模控制器來實現兩個混沌系統之間的同步。文獻[11]設計一個模糊自適應觀測器來實現帶有非線性和死區輸入的混沌系統的投影同步。文獻[12]以帶有未知參數和非線性輸入的混沌系統作為研究對象，設計一個有限時間自適應控制器實現了兩個不同的混沌系統之間的同步控制。

在研究混沌同步的過程中，學者們大多將重點放在混沌系統無故障的情況，來設計合適的控制器進行同步控制。然而，在實際應用的過程中，傳感器、執行機構以及系統內部元件都不可避免地會發生故障，發生故障時傳統的控制方法就會失效，破壞了主從系統之間的混沌同步。混沌同步廣泛地應用在保密通信中，為了保證通信質量，設計一個可靠的容錯控制器，使當有故障發生時，仍能保證主從系統之間達到同步時非常必要的。

近年來，容錯控制引起了學者們的廣泛關注。容錯控制大體可以分為兩類，即被動容錯方法[13-14]和主動容錯方法[15-16]。被動容錯方法是利用魯棒控制技術設計具有固定參數的控制器來保證系統的性能和穩定性[17]。這種方法設計簡單，不需要在線計算和調節參數，但當可能出現的故障和系統冗雜增加時，控制器的設計將變得保守，所達到的控制效果不能令人滿意。相比于被動容錯控制，主動容錯控制方法可以有效的解決上述問題。主動容錯方法是指在故障發生后根據故障情況重新調整控制器參數，或改變控制器結構。主動容錯控制一般利用自適應技術和故障診斷分離(fault detection and isolation，FDI)技術來實現。基于FDI的主動容錯方法可以利用FDI機構提供故障信息，從而設計有效的控制器，但FDI時常會出現誤報、漏報和傳輸延時等情況，使得提供的信息不夠準確。基于自適應技術的容錯控制方法不需要獲知準確的故障信息，避免了上述可能出現的問題，是一種有效的容錯控制手段。文獻[18]結合線性矩陣不等式技術和自適應技術，設計一個自適應容錯控制器，實現了對飛行器跟蹤的容錯控制。文獻[19]以帶有不確定參數和執行器故障的線性系統為研究對象，設計一個魯棒自適應容錯控制器，在有故障發生時仍能保證系統狀態漸近穩定。文獻[20]提出一個積分型自適應滑模容錯控制方法應用在航天器姿態控制中，保證了系統的穩定性并提高了系統性能指標。

然而，到目前為止，國內外針對混沌同步的容錯控制的相關研究成果卻很少，因此，本文在上述研究成果的基礎上，以帶有執行器故障、外界干擾以及非線性不確定性的混沌系統作為研究對象，設計一個魯棒自適應容錯控制器，即使系統有故障發生時，仍能保證兩個混沌系統之間的同步。不需要提前知道準確的故障信息，以及非線性不確定性和外界干擾的上界，并根據李雅普諾夫穩定性定理，給出了同步誤差系統穩定性的證明。最后，以數值仿真的形式證明了魯棒自適應容錯控制器的有效性和可行性。

1 系統模型與問題描述

符號標記：R代表實數集，I代表適合維數的單位矩陣。對于矩陣M，MT代表它的轉置，‖·‖代表歐幾里得范數，(i=1,2,…,N)定義為I[1,N]。

考慮下列一類不確定的主從混沌系統：

(1)

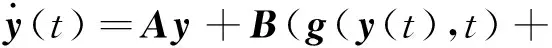
E(y(t),y(t-τ),t)+

d(t)+uF(t))。

(2)

其中:x(t)∈Rn和y(t)∈Rn分別代表主系統和從系統的狀態變量；A∈Rn×n和B∈Rn×m是常數矩陣；g(x(t),t)和g(y(t),t)為非線性函數，滿足Lipschitz條件；E(y(t),y(t-τ),t)∈Rm是未知的非線性時延函數；d(t)∈Rm是外部擾動。

(3)

故障模型具體表示方式如表1所示。

表1 故障模型Table 1 Fault mode

定義

ρju(t)+σjus(t)。

那么，有如上結構的算子集可表示為

也可以定義為

其中Nρj包含最多有2m個元素。

為了方便下文的描述，對于所有的故障模式L，我們使用下列統一的執行器故障模型

uF(t)=ρu(t)+σus(t)。

(4)

其中ρ=diag{ρ1,ρ2,…,ρm}。

定義主從系統之間的誤差為e(t)=y(t)-x(t)，那么可以得到同步誤差系統為

BE(y(t),y(t-τ),t)+

Bd(t)+BuF(t)。

(5)

為了方便下文控制器的設計，給出下列幾個假設。

假設1 對于?x∈Rn和?y∈Rn，非線性函數g(·)滿足下列Lipschitz條件

‖g(y,t)-g(x,t)‖≤γ‖y-x‖。

(6)

其中γ是未知的正常數。

假設2 對于?y∈Rn，非線性時延項滿足下列條件

‖E(y(t),y(t-τ),t)‖≤λ1‖y(t)‖+λ2‖y(t-τ)‖。

(7)

其中：λ1，λ2>0是未知的常數。

假設4 考慮同步誤差系統(5)，存在一個未知的正數α，對于所有可能的執行器故障模式都滿足下列不等式

‖eT(t)PBρBTPe(t)‖≥α‖eT(t)PB‖2。

(9)

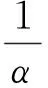
假設5 (A,B)是可控的，并存在一個常數矩陣K0，使得矩陣A-BK0滿足Hurwitz。

注1：假設1和假設2表明，調節參數γ，λ1和λ2可使不確定非線性項和非線性時延項滿足不等式成立的條件，文獻[22]、文獻[23]都做出了類似的假設。假設3說明非參數化卡死故障和外界擾動都是有界的，根據設計的自適應律可以估計上界的值。假設4說明，當帶有故障的執行器仍然有效時，即ρi不全為0(i∈I[1,m])時，式(9)成立；當所有的執行器都無效時，即ρi=0(i∈I[1,m])，假設4不再成立。

令

(10)

(11)

2 魯棒自適應容錯控制器設計

在本節中，針對同步誤差系統(5)，設計一個魯棒自適應容錯控制器，使得無論執行器是否有故障發生，都能夠保證同步誤差系統漸近穩定，即實現主從系統達到同步。

魯棒自適應容錯控制器u(t)設計為如下形式

u(t)=-K0e+K(t)。

(12)

其中K0可以由等式(10)得到，K(t)為

(13)

其中

(14)

自適應律設計為如下形式：

(15)

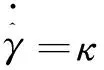
(16)

(17)

(18)

(19)

旅游翻譯要求譯者向作者和讀者靠攏，采取相應于譯文作者和讀者所使用的源語表達方式，來傳達原文的內容。博物館中常使用歸化翻譯是為了讓外國友人更好地理解相關信息。

證明：當系統有執行器發生故障時，將式(4)帶入式(5)中得到同步誤差系統為：

BE(y(t),y(t-τ),t)+Bd(t)+

B(ρu(t)+σus(t))。

(20)

選取Lyapunov函數為V(t)=V1(t)+V2(t)，其中：

(21)

(22)

對式(21)求導并結合誤差系統(20)得到

eT(t)PB(g(y(t),t)-g(x(t),t))+

eT(t)PBE(y(t),y(t-τ),t)+

eT(t)PBd(t)+eT(t)PB(ρu(t)+

σus(t))。

(23)

對上式整理得到

P(A-BK0))e(t)+eT(t)PBK0e(t)+

eT(t)PB(g(y(t),t)-g(x(t),t))+

eT(t)PBE(y(t),y(t-τ),t)+

eT(t)PBd(t)+eT(t)PB(ρu(t)+

σus(t))。

(24)

由式(10)和式(11)可知

eT(t)PB(g(y(t),t)-g(x(t),t))+

eT(t)PBE(y(t),y(t-τ),t)+

eT(t)PBd(t)+eT(t)PB(ρu(t)+

σus(t))。

(25)

‖eT(t)PB‖‖(g(y(t),t)-g(x(t),t))‖+

‖eT(t)PB‖‖E(y(t),y(t-τ),t)‖+

‖eT(t)PB‖‖d(t)‖+

‖eT(t)PB‖‖σ‖‖us(t)‖+

eT(t)PBρu(t)。

(26)

根據假設1～3可得到：

γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

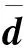
eT(t)PBρu(t)。

(27)

根據式(12)，將u(t)帶入上式，得到

eT(t)PBρK0e(t)+eT(t)PBρK(t)+

γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

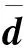
(28)

eT(t)PBρK(t)+γ‖eT(t)PB‖‖e(t)‖+λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

(29)

eT(t)PBρK(t)+γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

(30)

γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

(31)

γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

(32)

根據式(22)，對V2(t)求導，得到

(33)

將自適應律(15)～式(19)帶入上式，得到

(34)

2‖eT(t)PB‖‖K0e(t)‖-

γ‖eT(t)PB‖‖e(t)‖+

λ1‖eT(t)PB‖‖y(t)‖+

λ2‖eT(t)PB‖‖y(t-τ)‖+

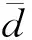
(35)

化簡得到

‖eT(t)PB‖φ(t)。

(36)

(37)

由上式可以得出，帶有執行器故障、非線性不確定性和外部擾動的混沌同步誤差系統(5)是漸進穩定的，當t→∞時，e(t)→0，即y(t)→x(t)，說明使用所設計的控制器，能夠實現主從混沌系統容錯同步控制。

注2：當執行器沒有故障發生時，即ρi=1且σi=0(i∈I[1,m])時，混沌系統的主從容錯同步控制就變成了一般的主從混沌同步控制問題，我們所設計的魯棒自適應控制器u(t)仍是有效的，假設4也仍然成立。

注3：在實際應用中，執行器故障、非線性不確定性和外界干擾等因素都會限制和影響控制器的使用，在選擇控制對象時，將這些可能影響控制器使用的因素都考慮在內，提高了控制器的可靠性，使得控制器更加符合工程應用。

3 系統仿真研究

3.1 系統仿真參數設定

為了驗證上述理論研究的正確性以及所設計的魯棒自適應容錯控制律的有效性，本節利用Matlab數值仿真的形式進行驗證，選擇經典的蔡氏混沌電路作為仿真模型。蔡氏電路是由美籍華裔學者蔡少棠在1983年提出的一種三階非線性自治電路，它能表現出標準的混沌行為。蔡氏電路的狀態方程形式為[22]：

(38)

其中:f(x1)=bx1+0.5(a-b)(|x1+1|-|x1-1|)，選擇a=-1.28，b=-0.69，那么，系統(37)可以寫成和混沌主系統(1)相同的形式

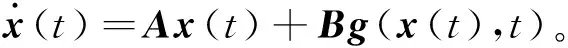
(39)

其中:

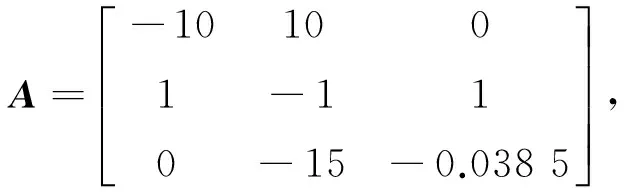
(40)

考慮到混沌系統模型帶有執行器故障、非線性時延和外界干擾，混沌從系統(2)可以寫為

E(y(t),y(t-τ),t)+

d(t)+uF(t))。

(41)

其中，

E(y(t),y(t-τ),t)=

(42)

主系統的初始條件為x(0)=[0.1,-0.1,-0.1]T，帶有非線性時延和外界擾動的從系統的初始條件為y(0)=[0.15,-0.15,-0.15]T，τ=1。圖1和圖2分別為主系統和從系統的混沌吸引子。

圖1 主系統混沌吸引子Fig.1 Chaotic attractor of master system

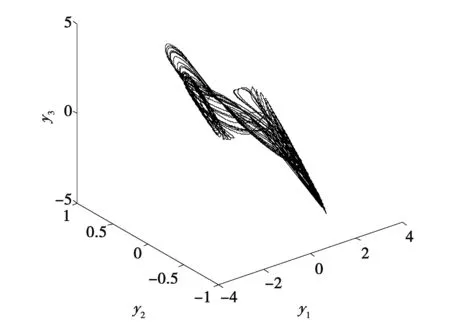
圖2 從系統混沌吸引子Fig.2 Chaotic attractor of slave system

考慮幾種可能的故障模型：

在仿真中，需要求出控制參數K0和P，根據等式(10)～式(11)，求得

給定Q為3階單位矩陣，求出P為

3.2 仿真結果分析

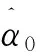
圖3 同步誤差的變化曲線Fig.3 Synchronization error

圖4 控制參數K(t)的變化曲線Fig.4 Curves of controller parameters K(t)

圖5 控制律的變化曲線Fig.5 Adaptive fault-tolerant control law

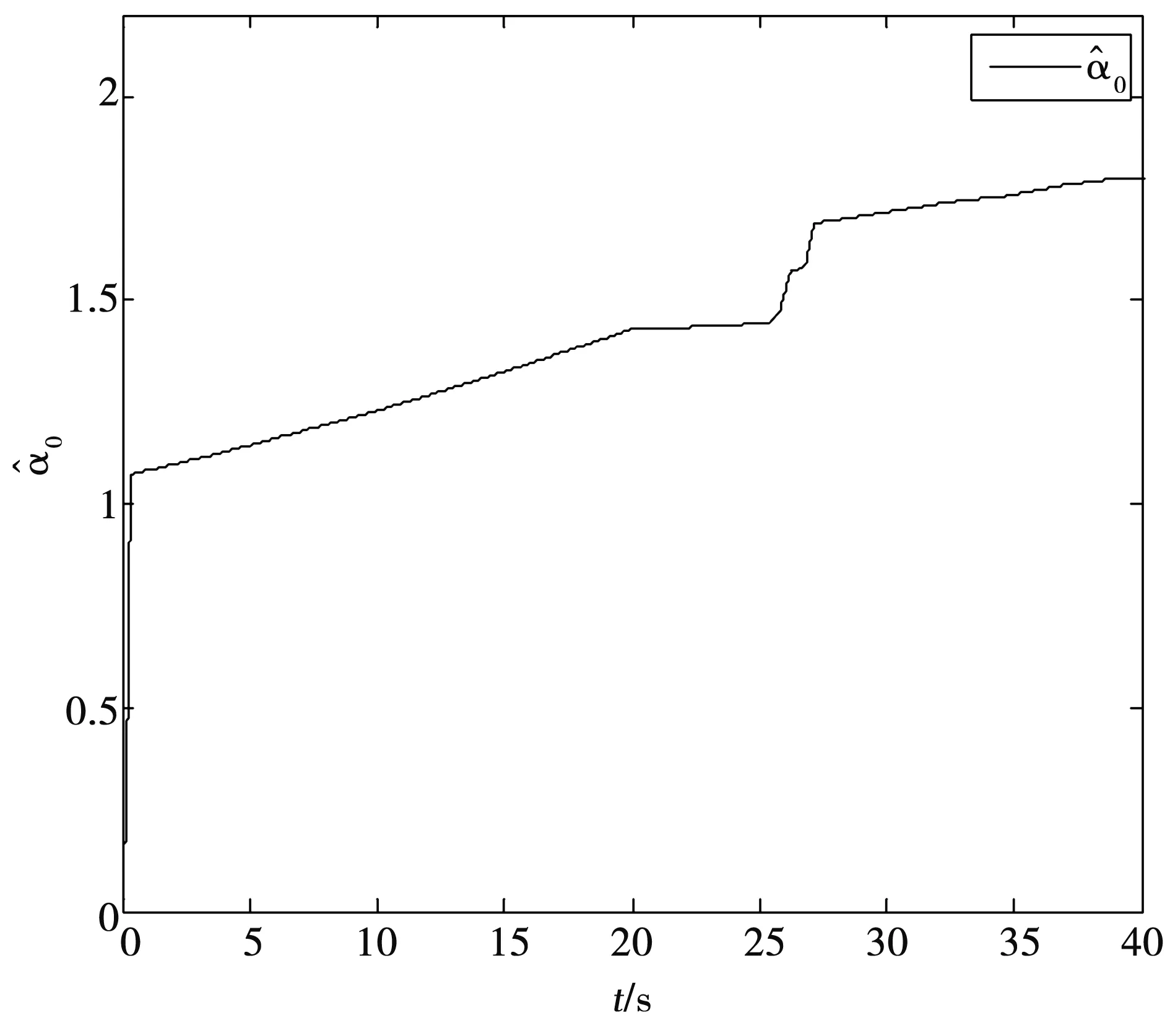
圖6 α0的估計值Fig.6 Estimate of unknown parameter α0

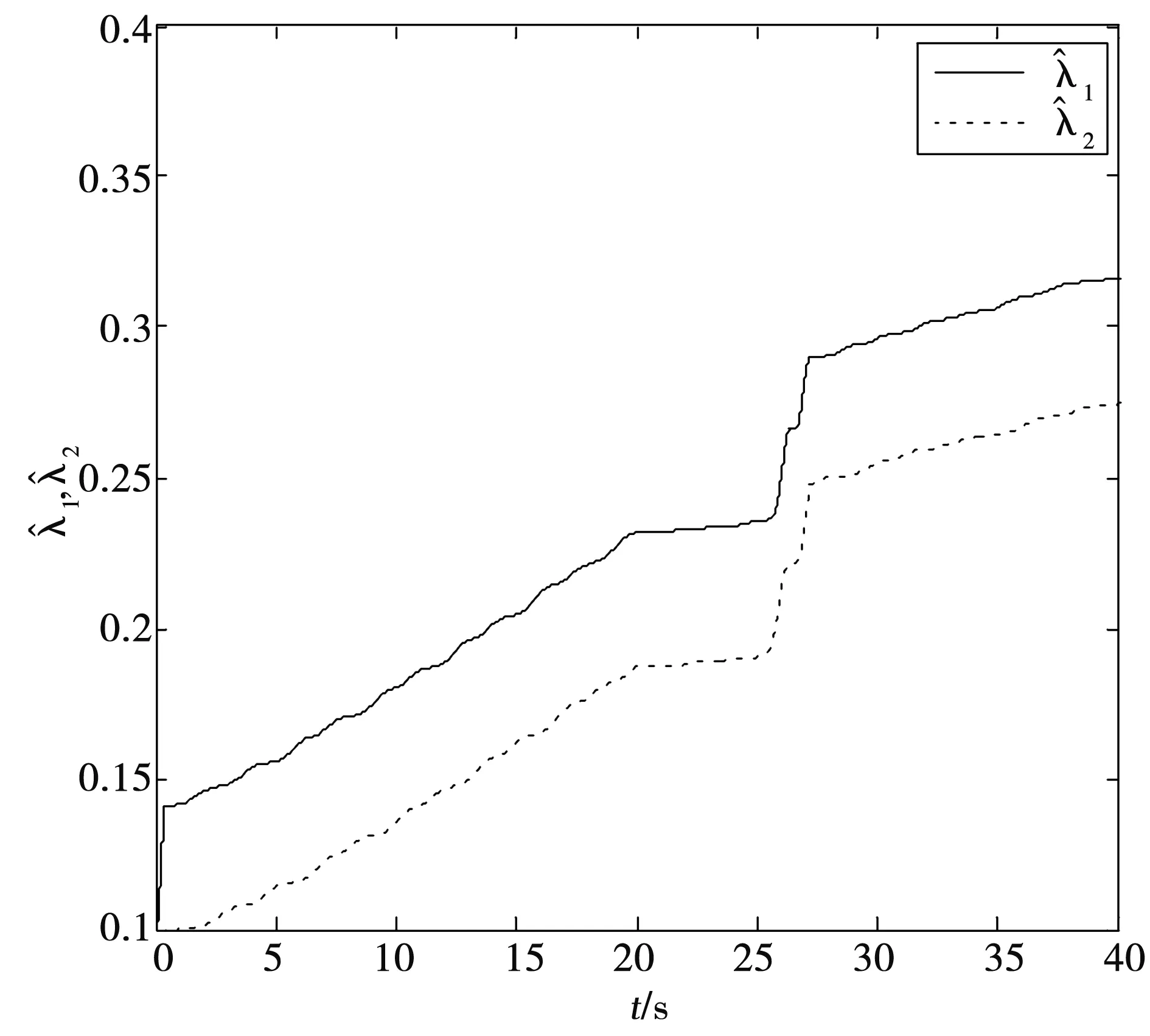
圖7 λ1和λ2的估計值Fig.7 Estimate of unknown parameters λ1 and λ2

圖8 γ的估計值Fig.8 Estimate of unknown parameter γ

圖的估計值Fig.9 Estimate of unknown parameter system

從圖3來看可知，故障沒有發生時，在控制律的作用下，同步誤差很快收斂到零點，在t=20 s時，執行器有故障發生，但在控制作用下同步誤差仍能很快地收斂到零點，主系統和從系統仍能達到同步。從圖4和圖5來看可知，為了使同步誤差快速收斂到零點，一開始控制律變化較大，在同步誤差收斂到零點后，控制律趨于平穩，在故障發生時，控制作用迅速變化又使誤差快速收斂到零點，使主從系統達到同步。從圖6～圖9可知，未知參數的估計值不需要收斂于它的真實值，這并不影響控制器的使用以及同步誤差收斂于零點的情況[23-24]。

4 結 論

本文設計一個魯棒自適應容錯控制律，實現了帶有執行器故障、非線性不確定性和外界擾動的主從混沌系統之間的同步容錯控制。不需要提前知曉準確的故障信息以及非線性不確定性和外界擾動的上界，利用自適應控制技術，設計合適的自適應律來估計系統中未知量的值。結合自適應控制方法，設計了一個魯棒自適應容錯控制律，根據李雅普諾夫穩定性，證明了同步誤差系統的漸近穩定性，并將蔡氏混沌電路作為仿真對象，仿真結果表明，無論執行器是否有故障發生，同步誤差都能夠很快的收斂到零點，實現了主從混沌系統之間的同步容錯控制，本文所設計的控制律有較強的魯棒性和容錯能力。

[1] LU J, WU X,Lü J. Synchronization of a unified chaotic system and the application in secure communication[J]. Physics Letters A, 2002, 305(6): 365.

[2] GUO L, HU M, XU Z, et al.Synchronization and chaos control by quorum sensing mechanism[J]. Nonlinear Dynamics, 2013, 73(3):1253.

[3] CHENG C J.Robust synchronization of uncertain unified chaotic systems subject to noise and its application to secure communication[J]. Applied Mathematics and Computation, 2012, 219(5): 2698.

[4} Yassen M. Controlling chaos and synchronization for new chaotic system using linear feedback control[J]. Chaos, Solitons & Fractals, 2005, 26(3):913.

[5] 陳志盛, 孫克輝, 張泰山. Liu混沌系統的非線性反饋同步控制[J]. 物理學報, 2005, 54(6):2580. CHEN Zhisheng, SUN Kehui, ZHANG Taishan. Nonlinear feedback synchronization control of Liu chaotic system[J]. 2005, 54(6):2580.

[6] PARK J H. Adaptive synchronization of a unified chaotic system with an uncertain parameter[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(2): 201.

[7] CHEN D, ZHANG R, MA X, et al.Chaotic synchronization and anti-synchronization for a novel class of multiple chaotic systems via a sliding mode control scheme[J]. Nonlinear Dynamics, 2012, 69(1-2): 35.

[8] 李秀春, 谷建華, 王云嵐, 等. 一類帶有未知參數的受擾混沌系統的觀測器同步[J]. 物理學報, 2011, 60(3): 030505. LI Xiuchun, GU Jianhua,WANG Yunlan, et al. Observer synchronization method for a class of perturbed chaotic systems with unknown parameters[J]. 2011, 60(3): 030505.

[9] 王銀河, 高子林, 王欽若, 等. 基于自適應模糊邏輯系統的一類混沌系統同步控制[J]. 控制與決策, 2013, 28(9): 1309. WANG Yinhe,GAO Zilin, WANG Qinruo, et al. Synchronization control for a class of chaotic systems based on adaptive fuzzy logic systems[J]. Control and Decision, 2013, 28(9): 1309.

[10] AGHABABA M P, FEIZI H. Design of a sliding mode controller for synchronizing chaotic systems with parameter and model uncertainties and external disturbances[J]. Transactions of the Institute of Measurement and Control, 2012, 34(8): 990.

[11] BOULKROUNE A, M′SAAD M. Fuzzy adaptive observer-based projective synchronization for nonlinear systems with input nonlinearity[J]. Journal of Vibration and Control, 2011, 14(1):12.

[12] AGHABABA M P,AGHABABA H P. A general nonlinear adaptive control scheme for finite-time synchronization of chaotic systems with uncertain parameters and nonlinear inputs[J]. Nonlinear Dynamics, 2012, 69(4):1903.

[13] YANG G H, WANG J L,SOH Y C. Reliable Hcontroller design for linear systems[J]. Automatica, 2001, 37(5): 717.

[14] ZHANG D, WANG Z, HU S. Robust satisfactory fault-tolerant control of uncertain linear discrete-time systems: an LMI approach[J]. International Journal of Systems Science, 2007, 38(2):151.

[15] TANG X, TAO G, JOSHI S M. Adaptive actuator failure compensation for nonlinear MIMO systems with an aircraft control application[J]. Automatica, 2007, 43(11): 1869.

[16] FAN L L,SOGN Y D. On fault-tolerant control of dynamic systems with actuator failures and external disturbances[J]. Acta Automatica Sinica, 2010, 36(11): 1620.

[17] 金小崢, 楊光紅, 常曉恒, 等. 容錯控制系統魯棒H和自適應補償設計[J]. 自動化學報, 2013, 39(1): 31. JIN Xiaozheng, YANG Guanghong, CHANG Xiaoheng, et al. Robust fault-tolerant Hcontrol with adaptive compensation[J]. Acta Automatica Sinica, 2013, 39(1): 31.

[18] YE D, YANG G H. Adaptive fault-tolerant tracking control against actuator faults with application to flight control [J]. IEEE Transactions on Control Systems Technology, 2006, 14(6): 1088.

[19] LI X J, YANG G H. Robust adaptive fault-tolerant control for uncertain linear systems with actuator failures[J]. Control Theory & Applications, IET, 2012, 6(10):1544.

[20] QINGLEI H, ZHANG Y, XING H, et al.Adaptive integral-type sliding mode control for spacecraft attitude maneuvering under actuator stuck failures[J]. Chinese Journal of Aeronautics, 2011, 24(1): 32.

[21] CHEN M,CHEN W.Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems[J]. Chaos, Solitons & Fractals, 2009, 41(5): 2716.

[22] MAHMOUD M S, AL-RAYYAAH A.Adaptive control of systems with mismatched non-linearities and time-varying delays using state measurements[J]. Control Theory & Applications, IET, 2010, 4(1):27.

[23] HAO L Y, YANG G H. Fault tolerant control for a class of uncertain chaotic systems with actuator saturation[J]. Nonlinear Dynamics, 2013, 73(4): 2133.

[24] JIN X, YANG G, LI Y. Robust fault-tolerant controller design for linear time-invariant systems with actuator failures: an indirect adaptive method[J]. Journal of Control Theory and Applications, 2010, 8(4): 471.

[25] 高慶忠,關煥新,于子淞,等. 自適應補償器永磁同步電機積分型連續滑模控制[J]. 電機與控制學報,2017,21(2):103. GAO Qingzhong, GUAN Huanxin, YU Zisong. Integral continuous sliding mode control strategy with adaptive compensator for permanent magnet synchronous motor[J]. Electric Machines and Control, 2017, 21(2): 103.

[26] 王琦, 陳龍勝. 非仿射純反饋不確定系統預設性能魯棒自適應控制[J]. 電機與控制學報, 2017, 21(2):109. WANG Qi, CHEN Longsheng. Prescribed performance adaptive robust control for a class of uncertain non-affine pure feedback system[J]. Electric Machines and Control, 2017, 21(2):109.

(編輯：賈志超)

Rubostadaptivefault-tolerantsynchronizationcontrolforuncertainchaoticsystems

DENG Li-wei， SONG Ge， GAO Jun-shan

(School of Automation, Harbin University of Science and Technology,Harbin 150080, China)

A robust adaptive fault-tolerant control scheme is designed to achieve the master-slave fault-tolerant synchronization for a class of chaotic systems with actuator failures, nonlinear uncertainties and external disturbances. Both accurate information of faults and upper bound of external disturbances are unknown,and the adaptive laws are proposed to estimate the unknown parameters online. Combined with adaptive control technology, a robust adaptive fault-tolerant controller was constructed to realize synchronization between master and slave systems whether the faults happen or not. A numerical simulation example of the classical chua′s circuit system was given,and the effectiveness and applicability of the proposed control scheme was proved by the simulation results.

adaptive control; fault-tolerant control; chaos synchronization; actuator failures; external disturbances

2016-07-19

黑龍江省自然科學基金(F201307)

鄧立為(1983—)，男，博士，講師，研究方向為分數階混沌系統、非線性控制； 宋 歌(1993—)，女，碩士研究生，研究方向為混沌系統； 高俊山(1962—)，男，博士，教授，研究方向為自動控制、混沌理論、魯棒控制。

宋 歌

10.15938/j.emc.2017.08.016

O 415.5/O 231.2

:A

:1007-449X(2017)08-0114-09