數形結合在初中數學課堂中的妙用

甘肅省靖遠縣高灣中學 韓 軍

數形結合在初中數學課堂中的妙用

甘肅省靖遠縣高灣中學 韓 軍

所謂“數形”結合，就是通過數（數量關系）與形（空間形式）的相互轉化、互相利用來解決數學問題的一種思想方法。數形結合既是一個重要的數學思想，又是一種常用的數學方法。它可將抽象的數學語言與直觀的圖形相結合，使抽象思維與形象思維結合。數與形是數學教學研究對象的兩個側面，把數量關系和空間形式結合起來去分析問題、解決問題，就是數形結合思想。“數形結合”可以借助簡單的圖形、符號和文字所作的示意圖，促進學生形象思維和抽象思維的協調發展，溝通數學知識之間的聯系，從復雜的數量關系中凸顯最本質的特征。數形結合方法的實質是將抽象的數學語言與直觀的圖形結合起來。

數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來，由數思形，以形想數，通過“以形助數”或“以數解形”，即通過抽象思維與形象思維的結合，可以使復雜問題簡單化、抽象問題具體化，從而起到優化解題途徑的目的。

一、以形助數

1．利用數形結合（數軸）解數與式

應用1：點A在數軸上距離原點3個單位長度，且位于原點左側。若一個點從點A處向右移動4個單位長度，再向左移動1個單位長度，此時終點所表示的是什么數？

分析：首先讓學生正確畫出數軸，由“點A在數軸上距離原點3個單位長度，且位于原點左側”確定點A所表示的數是-3，用數軸上的點表示，這種把給定的數（-3）用數軸上的點（A）表示，是由“數”到“形”的思維過程。一個點從點A處向右移動4個單位長度，到點A＇處，則點A＇表示的數是1，再向左移動1個單位長度到點A＂處，則點A＂表示的數是0，因此此時終點所表示的數是0。這種指出數軸上已知點所表示的數，是由“形”到“數”的思維過程。這道題從兩個側面體現出數形結合的思想。借助數形結合解這類題既方便又直觀。

解：如圖，點A表示的數為-3，向右移動4個單位長度到點A＇，點A＇表示的數為1，再向左移動1個單位到點A＂，點A＂表示的數為0。所以，此時終點所表示的數是0。

應用2：解方程：-3x2+22x-24=0。

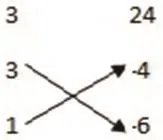
3×（-6）+1×（-4）=-22。

解：-3x2+22x-24=0，

3x2-22x+24=0 ，

（3x-4）（x-6）=0 ，

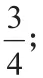
這種是將數量關系與直觀的幾何圖形結合起來，由數思形，使抽象問題具體化，從而起到優化解題途徑的目的。

2．利用數形結合解決“追趕小明”（方程）問題

應用1：小明每天早上要在7∶50之前趕到距家1000m的學校上學。一天，小明以80m/min的速度出發，5min后，小明的爸爸發現他忘了帶語文書。于是，爸爸以180m/min的速度去追小明，并且在途中追上了他。

（1）爸爸追上小明用了多長時間？

（2）追上小明時，距離學校還有多遠？

分析：當爸爸追上小明時，兩人所行距離相等.在解決這個問題時，要抓住這個等量關系。

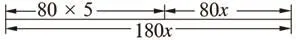
解：（1）設爸爸追上小明用了xmin。

根據題意，得 180x=80x+80×5，

化簡，得100x=400，

解得x=4。

因此，爸爸追上小明用了4min。

（2）180×4=720（m），1000-720=280（m）。

所以，追上小明時，距離學校還有280m。

分析：應鼓勵學生通過觀察、分析找出其中的等量關系，并嘗試借助“線段圖”分析復雜行程問題中的數量關系。這是一個數學化的過程，發展文字語言、圖形語言、符號語言之間的轉化能力。

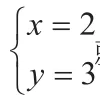
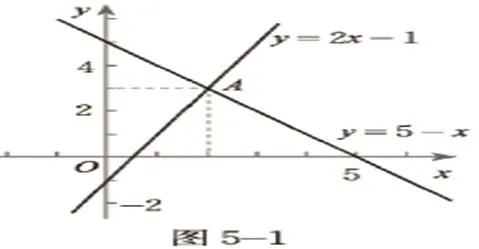
分析：學生從“形”上易于發現相應的函數圖象（直線）相交，而從“數”的方面也可以發現交點坐標適合這兩個方程，從而進一步體會二元一次方程與一次函數之間的關系以及方程組的解與函數圖象交點坐標之間的關系，體會數形結合思想，發展幾何直觀。

3．數形結合在“燒煤取暖”（不等式）問題中的應用

解不等式②，得x≥4。

在同一條數軸上表示不等式①②的解集，如圖：

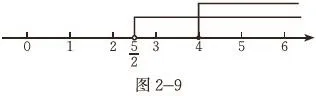
所以，原不等式組的解集是x≥4。

利用數軸表示不等式組的解集（找公共部分）是關鍵。這種表示反映了圖形和數量的對應關系，再現了數形結合思想。

二、以數解形——函數及其圖象凸顯的數形結合

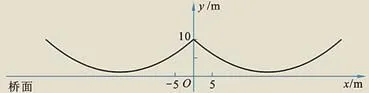
（1）鋼纜的最低點到橋面的距離是多少？

（2）兩條鋼纜最低點之間的距離是多少？

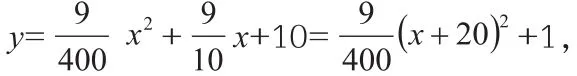
因此頂點的坐標為（-20，1），

所以，鋼纜的最低點到橋面的距離是1m。兩條鋼纜最低點之間的距離是40m。

[1]馬復．數學七年級上冊及教師教學用書[M]．北京：北京師范大學出版社，2013年6月出版．

[2]馬復．數學八年級上冊及教師教學用書[M]．北京：北京師范大學出版社，2014年7月出版．

[3]馬復．數學八年級下冊及教師教學用書[M]．北京：北京師范大學出版社，2014年11月出版．

[4]馬復．數學九年級上冊及教師教學用書[M]．北京：北京師范大學出版社，2014年6月出版．

[5]馬復．數學九年級下冊及教師教學用書[M]．北京：北京師范大學出版社，2014年11月出版．